安徽省马鞍山市2021-2022学年九年级上学期期中考试数学试卷(word解析版)
文档属性
| 名称 | 安徽省马鞍山市2021-2022学年九年级上学期期中考试数学试卷(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 21:12:48 | ||
图片预览




文档简介
2021-2022学年第一学期九年级数学期中试题卷
一、选择题(每小题3分,共30分)
1.下列函数表达式中,一定是二次函数的是( )
A.y=3x﹣1 B.y=ax2+bx+c C.y=2x2﹣2x+1 D.y=x2+
2.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD AB
3.反比例函数,下列说法不正确的是( )
A.图象经过点(1,﹣1) B.图象位于第二、四象限
C.图象关于直线y=﹣x对称 D.y随x的增大而增大
4.将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为( )
A.y=(x+3)2+5 B.y=(x﹣3)2+5 C.y=(x+5)2+3 D.y=(x﹣5)2+3
5.下面四组图形中,必是相似三角形的为( )
A.两个直角三角形相似
B.两条边对应成比例,一个对应角相等的两个三角形相似
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
6.在同一平面直角坐标系中,函数y=kx2+k与y=的图象可能是( )
7.已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法错误的是( )
x … ﹣1 0 1 3 …
y … ﹣3 1 3 1 …
A.a<0 B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0 D.若点(5,y1)、(﹣,y2)都在函数图象上,则y1<y2
8.如图所示,AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:AC=( )
A.1:4 B.1:5 C.1:6 D.1:7
9.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
10.已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.0≤t≤1 B.﹣1≤t≤0 C.﹣5≤t≤4 D.﹣1≤t≤1
填空题(每小题3分,共24分)
11.抛物线y=3(x﹣1)2+8的顶点坐标为 .
12.已知:==,且3a﹣2b+c=9,则2a+4b﹣3c= .
13.已知点A(﹣1,y1),B(2,y2)在反比例函数y=(k<0)的图象上,则y1 y2(填“>”“<”或“=”)
14.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则b的值为 .
15.当﹣4≤x≤2时,函数y=﹣x2﹣6x﹣7的取值范围为 .
16.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k= .
17.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
18.在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 .
解答题(共6小题,46分)
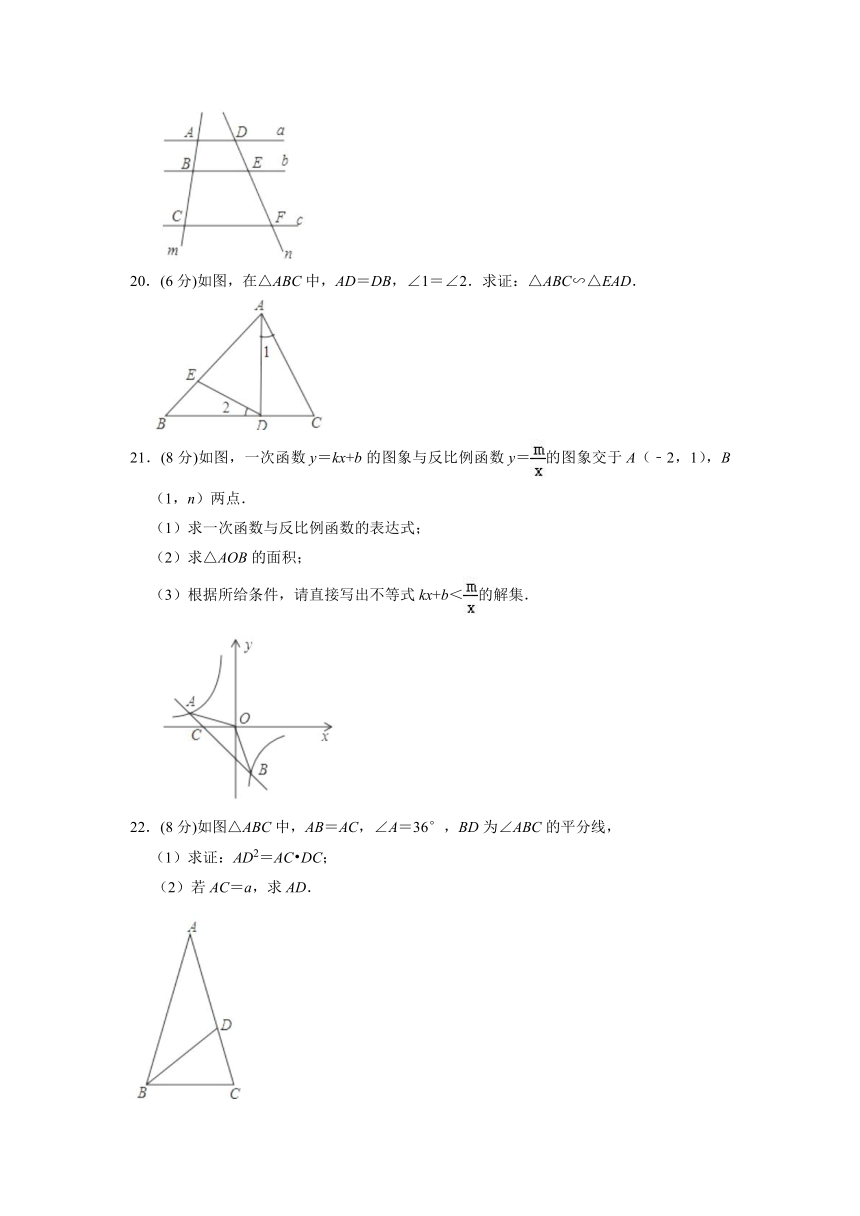
19.(6分)如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
若AB:BC=2:5,DF=10,求EF的长.
20.(6分)如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
21.(8分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A(﹣2,1),B(1,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积;
(3)根据所给条件,请直接写出不等式kx+b<的解集.
22.(8分)如图△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,
(1)求证:AD2=AC DC;
(2)若AC=a,求AD.
23.(9分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
24.(9分)如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.下列函数表达式中,一定是二次函数的是( )
A.y=3x﹣1 B.y=ax2+bx+c C.y=2x2﹣2x+1 D.y=x2+
【分析】根据二次函数的定义:一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数进行分析.
【解答】解:A、是一次函数,故此选项错误;
B、当a=0时,y=ax2+bx+c不是二次函数,故此选项错误;
C、是二次函数,故此选项正确;
D、含有分式,不是二次函数,故此选项错误;
故选:C.
2.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD AB
【分析】根据相似三角形的判定逐一判断可得.
【解答】解:A、由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B、由不能判定△ACD∽△ABC,此选项符合题意;
C、由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D、由AC2=AD AB,即=,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故选:B.
3.反比例函数,下列说法不正确的是( )
A.图象经过点(1,﹣1) B.图象位于第二、四象限
C.图象关于直线y=﹣x对称 D.y随x的增大而增大
【分析】反比例函数y=(k≠0)的图象k>0时位于第一、三象限,在每个象限内,y随x的增大而减小;k<0时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.
【解答】解:A、图象经过点(1,﹣1),正确;
B、图象位于第二、四象限,故正确;
C、双曲线关于直线y=﹣x成轴对称,正确;
D、在每个象限内,y随x的增大而增大,故错误,
故选:D.
4.将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为( )
A.y=(x+3)2+5 B.y=(x﹣3)2+5 C.y=(x+5)2+3 D.y=(x﹣5)2+3
【分析】根据“上加下减,左加右减”的原则进行解答即可.
【解答】解:由“上加下减”的原则可知,将抛物线y=x2向上平移3个单位所得抛物线的解析式为:y=x2+3;
由“左加右减”的原则可知,将抛物线y=x2+3向右平移5个单位所得抛物线的解析式为:y=(x﹣5)2+3;
故选:D.
5.下面四组图形中,必是相似三角形的为( )
A.两个直角三角形相似
B.两条边对应成比例,一个对应角相等的两个三角形相似
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
【分析】根据等腰三角形的性质和相似三角形的判定方法得出A、B、C不一定相似,D一定相似;即可得出结果.
【解答】解:两个直角三角形不一定相似;
因为只有一个直角相等,
∴A不一定相似;
两条边对应成比例,一个对应角相等的两个三角形不一定相似;
因为这个对应角不一定是夹角;
∴B不一定相似;
有一个角为40°的两个等腰三角形不一定相似;
因为40°的角可能是顶角,也可能是底角,
∴C不一定相似;
有一个角为100°的两个等腰三角形一定相似;
因为100°的角只能是顶角,
所以两个等腰三角形的顶角和底角分别相等,
∴D一定相似;
故选:D.
6.在同一平面直角坐标系中,函数y=kx2+k与y=的图象可能是( )
【分析】分k>0和k<0分析两函数图象大致位置,对照四个选项即可得出结论.
【解答】解:当k>0时,函数y=kx2+k的图象开口向上,顶点坐标在y轴正半轴上,
此时,函数y=的图象在第一、三象限,
∴A选项中图形合适;
当k<0时,函数y=kx2+k的图象开口向下,顶点坐标在y轴负半轴上,
此时,函数y=的图象在第二、四象限,
∴无合适图形.
故选:A.
7.已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法错误的是( )
x … ﹣1 0 1 3 …
y … ﹣3 1 3 1 …
A.a<0 B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0 D.若点(5,y1)、(﹣,y2)都在函数图象上,则y1<y2
【分析】利用表中函数值的变换情况可判断抛物线的开口方向,则可对A进行判断;利用抛物线的对称性可得x=﹣1和x=4的函数值相等,则可对B进行判断;利用x=0和x=3时函数值相等可得到抛物线的对称轴方程,则可对C进行判断;利用二次函数的性质则可对D进行判断.
【解答】解:∵二次函数值先由小变大,再由大变小,
∴抛物线的开口向下,
∴a<0,
故A正确;
∵x=﹣1时,y=﹣3,
∴x=4时,y=﹣3,
∴二次函数y=ax2+bx+c的函数值为﹣2时,﹣1<x<0或3<x<4,
即方程ax2+bx+c=﹣2的负根在﹣1与0之间,正根在3与4之间,
故B错误;
∵抛物线过点(0,1)和(3,1),
∴抛物线的对称轴为直线x=,
∴﹣=>1,
∴2a+b>0,
故C正确;
∵(﹣,y2)关于直线x=的对称点为(,y2),
∵<5,
∴y1<y2,
故D正确;
故选:B.
8.如图所示,AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:AC=( )
A.1:4 B.1:5 C.1:6 D.1:7
【分析】作DH∥BF交AC于H,根据三角形中位线定理得到FH=HC,根据平行线分线段成比例定理得到,计算得到答案.
【解答】解:作DH∥BF交AC于H
∵AD是△ABC的中线,
∴BD=DC,
∴FH=HC,
∵DH∥BF,
∴
∴AF:FC=1:6,
∴AF:AC=1:7,
故选:D.
9.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
【分析】分为0<x≤2、2<x≤4两种情况,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
【解答】解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GH=EJ=x,
∴y=EJ GH=x2.
当x=2时,y=,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
y=FJ GH=(4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
10.已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.0≤t≤1 B.﹣1≤t≤0 C.﹣5≤t≤4 D.﹣1≤t≤1
【分析】找到最大值和最小值差刚好等于5的时刻,则t的范围可知.
【解答】解:如图1所示,当t等于0时,
∵y=﹣(x﹣1)2+4,
∴顶点坐标为(1,4),
当x=0时,y=3,
∴A(0,3),
当x=4时,y=﹣5,
∴C(4,﹣5),
∴当t=0时,
D(4,5),
∴此时最大值为5,最小值为0;
如图2所示,当t=﹣1时,
此时最小值为﹣1,最大值为4.
综上所述:﹣1≤t≤0,
故选:B.
填空题(每小题3分,共24分)
11.抛物线y=3(x﹣1)2+8的顶点坐标为 .
【分析】已知抛物线顶点式y=a(x﹣h)2+k,顶点坐标是(h,k).
【解答】解:∵抛物线y=3(x﹣1)2+8是顶点式,
∴顶点坐标是(1,8).
故答案为:(1,8).
12.已知:==,且3a﹣2b+c=9,则2a+4b﹣3c= .
【分析】根据题意列出三元一次方程组,求得a,b,c的值后,代入代数式求值.
【解答】解:由于==,3a﹣2b+c=9,
∴,
解得:b=7,a=5,c=8,
把a,b,c代入代数式得:
2a+4b﹣3c=2×5+4×7﹣3×8=14,
故本题答案为:14,
另解:设:===x,
则:a=5x,b=7x,c=8x
3a﹣2b+c=9可以转化为:15x﹣14x+8x=9,解得x=1
那么 2a+4b﹣3c=10x+28x﹣24x=14x=14.
故答案为:14.
13.已知点A(﹣1,y1),B(2,y2)在反比例函数y=(k<0)的图象上,则y1 y2(填“>”“<”或“=”)
【分析】先根据反比例函数的性质判断出函数图象所在的象限,再判断出在每一象限内的增减性,根据点A(﹣1,y1),B(2,y2)即可得出结论.
【解答】解:∵反比例函数y=中,k<0,
∴此函数的图象在二四象限,
∵A(﹣1,y1),B(2,y2),
∴点A在第二象限,点B在第四象限,
∴y1>0,y2<0,
∴y1>y2.
故答案为:>.
14.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则b的值为 .
【分析】根据(﹣2,n)和(4,n)可以确定函数的对称轴x=1,再由对称轴的x=即可求解;
【解答】解:抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,
可知函数的对称轴x=1,
∴=1,
∴b=2;
故答案为2.
15.当﹣4≤x≤2时,函数y=﹣x2﹣6x﹣7的取值范围为 .
【分析】先根据a=﹣1判断出抛物线的开口向下,故有最大值,可知对称轴x=﹣3,再根据﹣4≤x≤2,可知当x=﹣3时y最大,把x=2时y最小代入即可得出结论.
【解答】解:∵a=﹣1,
∴抛物线的开口向下,故有最大值,
∵对称轴x=﹣3,
∴当x=﹣3时y最大为2,
当x=2时y最小为﹣23,
∴函数y的取值范围为﹣23≤y≤2,
故答案为﹣23≤y≤2.
16.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k= .
【分析】首先根据反比例函数与正比例函数的图象特征,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于4,然后由反比例函数y=的比例系数k的几何意义,可知△AOC的面积等于|k|,从而求出k的值.
【解答】解:∵反比例函数与正比例函数的图象相交于A、B两点,
∴A、B两点关于原点对称,
∴OA=OB,
∴△BOC的面积=△AOC的面积=8÷2=4,
又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,
∴△AOC的面积=|k|,
∴|k|=4,
∵k>0,
∴k=8.
故答案为8.
17.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
【分析】根据折叠的性质得到BE=EF,根据相似三角形的性质即可得到结论.
【解答】解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
18.在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 .
【分析】根据题意可以将函数解析式化为顶点式,由抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,可以得到顶点的纵坐标为0或当x=0时y<0且当x=3时,y不小于0,从而可以求得x的取值范围.
【解答】解:∵点A的坐标为(3,0),抛物线y=x2﹣2x+n﹣1=(x﹣1)2+n﹣2与线段OA有且只有一个公共点,
∴n﹣2=0或,
解得,﹣2≤n<1或n=2,
故答案为:﹣2≤n<1或n=2.
解答题(共6小题,46分)
19.(6分)如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
若AB:BC=2:5,DF=10,求EF的长.
【分析】根据平行线分线段成比例定理得到,然后利用比例性质求EF即可.
【解答】解:∵a∥b∥c,
∴,
∴,
解得.
20.(6分)如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
【分析】根据已知得出∠C=∠ADE,进而利用相似三角形的判定方法得出答案.
【解答】证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
21.(8分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A(﹣2,1),B(1,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积;
(3)根据所给条件,请直接写出不等式kx+b<的解集.
【分析】(1)把点A(﹣2,1)代入反比例函数y=,得到关于m的一元一次方程,解之,得到m的值,即可得到反比例函数的解析式,把点B(1,n)代入反比例函数y=﹣得到关于n的一元一次方程,解之,即可得到n的值,得到点A和点B的坐标,利用待定系数法,解之,即可得到k和b的值,即可得到一次函数的表达式,
(2)把y=0代入一次函数y=﹣x﹣1,解之,得到点C的横坐标,根据点A和点B的纵坐标,分别求出△OAC和△OBC的面积,二者相加即可得到答案,
(3)根据函数图象,结合点A和点B的横坐标,即可得到答案.
【解答】解:(1)把点A(﹣2,1)代入反比例函数y=得:
1=,
解得:m=﹣2,
即反比例函数的解析式为:y=﹣,
把点B(1,n)代入反比例函数y=﹣得:
n=﹣2,
即点A的坐标为:(﹣2,1),点B的坐标为:(1,﹣2),
把点A(﹣2,1)和点B(1,﹣2)代入一次函数y=kx+b得:
,
解得:,
即一次函数的表达式为:y=﹣x﹣1,
(2)把y=0代入一次函数y=﹣x﹣1得:
﹣x﹣1=0,
解得:x=﹣1,
即点C的坐标为:(﹣1,0),OC的长为1,
点A到OC的距离为1,点B到OC的距离为2,
S△AOB=S△OAC+S△OBC
=+
=,
(3)如图可知:kx+b<的解集为:﹣2<x<0,x>1.
22.(8分)如图△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,
(1)求证:AD2=AC DC;
(2)若AC=a,求AD.
【分析】(1)根据两角对应相等证明△BCD∽△ABC,再根据相似三角形的性质即可得到;
(2)结合(1)的结论和已知条件可以得到关于x的方程,从而求解.
【解答】(1)证明:∵∠ABC=∠C=∠BDC,
∴△BCD∽△ABC.
∴,
又BC=BD=AD,
∴AD2=AC DC.
(2)解:∵AD2=AC DC,设AD=x,AC=AD+CD,
∴AD2=(AC-AD) AC,
x2=(a-x)a,
x(a+x)=a2,
x2+ax﹣a2=0,
x= (负值舍去).
即x= .
23.(9分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
【分析】(1)根据“活动区的面积=矩形空地面积﹣阴影区域面积”列出函数解析式便可,图形可得结论;
(2)根据题意可得y与x的关系式;
(3)根据二次函数的增减性及解一元二次方程可得结论;
【解答】解:(1)根据题意,绿化区的宽为:[30﹣(50﹣2x)]÷2=x﹣10
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500,
∵4个出口宽度相同,其宽度不小于14m,不大于26m,
∴12≤x≤18,
∴y=﹣4x2+40x+1500(12≤x≤18);
(2)y=﹣4x2+40x+1500=﹣4(x﹣5)2+1600,
∵a=﹣4<0,抛物线的开口向下,当12≤x≤18时,y随x的增大而减小,
∴当x=12时,y最大=1404,
答:活动区的最大面积为1404m2.
(3)设投资费用为w元,
由题意得,w=50(﹣4x2+40x+1500)+40×4x(x﹣10)=﹣40(x﹣5)2+76000,
∴当w=72000时,解得:x1=﹣5(不符合题意舍去),x2=15,
∵a=﹣40<0,
∴当x≥15时,w≤72000,
又∵12≤x≤18,
∴15≤x≤18,
∴当x=18时,投资费用最少,此时出口宽度为50﹣2x=50﹣2×18=14(m),
答:投资最少时活动区的出口宽度为14m.
24.(9分)如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
【分析】(1)利用待定系数法求解可得;
(2)利用待定系数法确定直线BC的解析式为y=﹣x+5,设D(x,﹣x2+4x+5),则E(x,﹣x+5),F(x,0),(0<x<5),则DE=﹣x2+5x,EF=﹣x+5,利用三角形的面积公式进行讨论:当DE:EF=2:3时,S△BDE:S△BEF=2:3;当DE:EF=3:2时,S△BDE:S△BEF=3:2,从而可得到关于x的方程,然后解方程求出x就看得到对应的D点坐标;
(3)先确定抛物线的对称轴,如图,设M(2,t),利用两点间的距离公式得到BC2=50,MC2=t2﹣10t+29,MB2=t2+9,利用勾股定理的逆定理分类讨论:当BC2+MC2=MB2时,△BCM为直角三角形,则50+t2﹣10t+29=t2+9;当BC2+MB2=MC2时,△BCM为直角三角形,则50+t2+9=t2﹣10t+29;当MC2+MB2=BC2时,△BCM为直角三角形,则t2﹣10t+29+t2+9=50,然后分别解关于t的方程,从而可得到满足条件的M点坐标.
【解答】解:(1)将A(﹣1,0),B(5,0)代入y=ax2+bx+5,
得:,
解得,
则抛物线解析式为y=﹣x2+4x+5;
(2)能.
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得,
解得,
所以直线BC的解析式为y=﹣x+5,
设D(x,﹣x2+4x+5),则E(x,﹣x+5),F(x,0),(0<x<5),
∴DE=﹣x2+4x+5﹣(﹣x+5)=﹣x2+5x,EF=﹣x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(﹣x2+5x):(﹣x+5)=2:3,
整理得3x2﹣17x+10=0,
解得x1=,x2=5(舍去),此时D点坐标为(,);
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(﹣x2+5x):(﹣x+5)=3:2,
整理得2x2﹣13x+15=0,
解得x1=,x2=5(舍去),此时D点坐标为(,);
综上所述,当点D的坐标为(,)或(,)时,直线BC把△BDF分成面积之比为2:3的两部分;
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t﹣5)2=t2﹣10t+29,MB2=(2﹣5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2﹣10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2﹣10t+29,解得t=﹣3,此时M点的坐标为(2,﹣3);
当MC2+MB2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2﹣10t+29+t2+9=50,解得t1=6,t2=﹣1,此时M点的坐标为(2,6)或(2,﹣1),
综上所述,满足条件的M点的坐标为(2,7),(2,﹣3),(2,6),(2,﹣1).
一、选择题(每小题3分,共30分)
1.下列函数表达式中,一定是二次函数的是( )
A.y=3x﹣1 B.y=ax2+bx+c C.y=2x2﹣2x+1 D.y=x2+
2.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD AB
3.反比例函数,下列说法不正确的是( )
A.图象经过点(1,﹣1) B.图象位于第二、四象限
C.图象关于直线y=﹣x对称 D.y随x的增大而增大
4.将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为( )
A.y=(x+3)2+5 B.y=(x﹣3)2+5 C.y=(x+5)2+3 D.y=(x﹣5)2+3
5.下面四组图形中,必是相似三角形的为( )
A.两个直角三角形相似
B.两条边对应成比例,一个对应角相等的两个三角形相似
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
6.在同一平面直角坐标系中,函数y=kx2+k与y=的图象可能是( )
7.已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法错误的是( )
x … ﹣1 0 1 3 …
y … ﹣3 1 3 1 …
A.a<0 B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0 D.若点(5,y1)、(﹣,y2)都在函数图象上,则y1<y2
8.如图所示,AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:AC=( )
A.1:4 B.1:5 C.1:6 D.1:7
9.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
10.已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.0≤t≤1 B.﹣1≤t≤0 C.﹣5≤t≤4 D.﹣1≤t≤1
填空题(每小题3分,共24分)
11.抛物线y=3(x﹣1)2+8的顶点坐标为 .
12.已知:==,且3a﹣2b+c=9,则2a+4b﹣3c= .
13.已知点A(﹣1,y1),B(2,y2)在反比例函数y=(k<0)的图象上,则y1 y2(填“>”“<”或“=”)
14.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则b的值为 .
15.当﹣4≤x≤2时,函数y=﹣x2﹣6x﹣7的取值范围为 .
16.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k= .
17.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
18.在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 .
解答题(共6小题,46分)
19.(6分)如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
若AB:BC=2:5,DF=10,求EF的长.
20.(6分)如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
21.(8分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A(﹣2,1),B(1,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积;
(3)根据所给条件,请直接写出不等式kx+b<的解集.
22.(8分)如图△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,
(1)求证:AD2=AC DC;
(2)若AC=a,求AD.
23.(9分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
24.(9分)如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.下列函数表达式中,一定是二次函数的是( )
A.y=3x﹣1 B.y=ax2+bx+c C.y=2x2﹣2x+1 D.y=x2+
【分析】根据二次函数的定义:一般地,形如y=ax2+bx+c(a、b、c是常数,a≠0)的函数,叫做二次函数进行分析.
【解答】解:A、是一次函数,故此选项错误;
B、当a=0时,y=ax2+bx+c不是二次函数,故此选项错误;
C、是二次函数,故此选项正确;
D、含有分式,不是二次函数,故此选项错误;
故选:C.
2.如图,下列条件中不能判定△ACD∽△ABC的是( )
A.∠ADC=∠ACB B. C.∠ACD=∠B D.AC2=AD AB
【分析】根据相似三角形的判定逐一判断可得.
【解答】解:A、由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B、由不能判定△ACD∽△ABC,此选项符合题意;
C、由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D、由AC2=AD AB,即=,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故选:B.
3.反比例函数,下列说法不正确的是( )
A.图象经过点(1,﹣1) B.图象位于第二、四象限
C.图象关于直线y=﹣x对称 D.y随x的增大而增大
【分析】反比例函数y=(k≠0)的图象k>0时位于第一、三象限,在每个象限内,y随x的增大而减小;k<0时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.
【解答】解:A、图象经过点(1,﹣1),正确;
B、图象位于第二、四象限,故正确;
C、双曲线关于直线y=﹣x成轴对称,正确;
D、在每个象限内,y随x的增大而增大,故错误,
故选:D.
4.将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为( )
A.y=(x+3)2+5 B.y=(x﹣3)2+5 C.y=(x+5)2+3 D.y=(x﹣5)2+3
【分析】根据“上加下减,左加右减”的原则进行解答即可.
【解答】解:由“上加下减”的原则可知,将抛物线y=x2向上平移3个单位所得抛物线的解析式为:y=x2+3;
由“左加右减”的原则可知,将抛物线y=x2+3向右平移5个单位所得抛物线的解析式为:y=(x﹣5)2+3;
故选:D.
5.下面四组图形中,必是相似三角形的为( )
A.两个直角三角形相似
B.两条边对应成比例,一个对应角相等的两个三角形相似
C.有一个角为40°的两个等腰三角形
D.有一个角为100°的两个等腰三角形
【分析】根据等腰三角形的性质和相似三角形的判定方法得出A、B、C不一定相似,D一定相似;即可得出结果.
【解答】解:两个直角三角形不一定相似;
因为只有一个直角相等,
∴A不一定相似;
两条边对应成比例,一个对应角相等的两个三角形不一定相似;
因为这个对应角不一定是夹角;
∴B不一定相似;
有一个角为40°的两个等腰三角形不一定相似;
因为40°的角可能是顶角,也可能是底角,
∴C不一定相似;
有一个角为100°的两个等腰三角形一定相似;
因为100°的角只能是顶角,
所以两个等腰三角形的顶角和底角分别相等,
∴D一定相似;
故选:D.
6.在同一平面直角坐标系中,函数y=kx2+k与y=的图象可能是( )
【分析】分k>0和k<0分析两函数图象大致位置,对照四个选项即可得出结论.
【解答】解:当k>0时,函数y=kx2+k的图象开口向上,顶点坐标在y轴正半轴上,
此时,函数y=的图象在第一、三象限,
∴A选项中图形合适;
当k<0时,函数y=kx2+k的图象开口向下,顶点坐标在y轴负半轴上,
此时,函数y=的图象在第二、四象限,
∴无合适图形.
故选:A.
7.已知二次函数y=ax2+bx+c与自变量x的部分对应值如表,下列说法错误的是( )
x … ﹣1 0 1 3 …
y … ﹣3 1 3 1 …
A.a<0 B.方程ax2+bx+c=﹣2的正根在4与5之间
C.2a+b>0 D.若点(5,y1)、(﹣,y2)都在函数图象上,则y1<y2
【分析】利用表中函数值的变换情况可判断抛物线的开口方向,则可对A进行判断;利用抛物线的对称性可得x=﹣1和x=4的函数值相等,则可对B进行判断;利用x=0和x=3时函数值相等可得到抛物线的对称轴方程,则可对C进行判断;利用二次函数的性质则可对D进行判断.
【解答】解:∵二次函数值先由小变大,再由大变小,
∴抛物线的开口向下,
∴a<0,
故A正确;
∵x=﹣1时,y=﹣3,
∴x=4时,y=﹣3,
∴二次函数y=ax2+bx+c的函数值为﹣2时,﹣1<x<0或3<x<4,
即方程ax2+bx+c=﹣2的负根在﹣1与0之间,正根在3与4之间,
故B错误;
∵抛物线过点(0,1)和(3,1),
∴抛物线的对称轴为直线x=,
∴﹣=>1,
∴2a+b>0,
故C正确;
∵(﹣,y2)关于直线x=的对称点为(,y2),
∵<5,
∴y1<y2,
故D正确;
故选:B.
8.如图所示,AD是△ABC的中线,E是AD上一点,AE:ED=1:3,BE的延长线交AC于F,AF:AC=( )
A.1:4 B.1:5 C.1:6 D.1:7
【分析】作DH∥BF交AC于H,根据三角形中位线定理得到FH=HC,根据平行线分线段成比例定理得到,计算得到答案.
【解答】解:作DH∥BF交AC于H
∵AD是△ABC的中线,
∴BD=DC,
∴FH=HC,
∵DH∥BF,
∴
∴AF:FC=1:6,
∴AF:AC=1:7,
故选:D.
9.如图,△ABC和△DEF都是边长为2的等边三角形,它们的边BC,EF在同一条直线l上,点C,E重合.现将△ABC沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点C移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
【分析】分为0<x≤2、2<x≤4两种情况,然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式,于是可求得问题的答案.
【解答】解:如图1所示:当0<x≤2时,过点G作GH⊥BF于H.
∵△ABC和△DEF均为等边三角形,
∴△GEJ为等边三角形.
∴GH=EJ=x,
∴y=EJ GH=x2.
当x=2时,y=,且抛物线的开口向上.
如图2所示:2<x≤4时,过点G作GH⊥BF于H.
y=FJ GH=(4﹣x)2,函数图象为抛物线的一部分,且抛物线开口向上.
故选:A.
10.已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.0≤t≤1 B.﹣1≤t≤0 C.﹣5≤t≤4 D.﹣1≤t≤1
【分析】找到最大值和最小值差刚好等于5的时刻,则t的范围可知.
【解答】解:如图1所示,当t等于0时,
∵y=﹣(x﹣1)2+4,
∴顶点坐标为(1,4),
当x=0时,y=3,
∴A(0,3),
当x=4时,y=﹣5,
∴C(4,﹣5),
∴当t=0时,
D(4,5),
∴此时最大值为5,最小值为0;
如图2所示,当t=﹣1时,
此时最小值为﹣1,最大值为4.
综上所述:﹣1≤t≤0,
故选:B.
填空题(每小题3分,共24分)
11.抛物线y=3(x﹣1)2+8的顶点坐标为 .
【分析】已知抛物线顶点式y=a(x﹣h)2+k,顶点坐标是(h,k).
【解答】解:∵抛物线y=3(x﹣1)2+8是顶点式,
∴顶点坐标是(1,8).
故答案为:(1,8).
12.已知:==,且3a﹣2b+c=9,则2a+4b﹣3c= .
【分析】根据题意列出三元一次方程组,求得a,b,c的值后,代入代数式求值.
【解答】解:由于==,3a﹣2b+c=9,
∴,
解得:b=7,a=5,c=8,
把a,b,c代入代数式得:
2a+4b﹣3c=2×5+4×7﹣3×8=14,
故本题答案为:14,
另解:设:===x,
则:a=5x,b=7x,c=8x
3a﹣2b+c=9可以转化为:15x﹣14x+8x=9,解得x=1
那么 2a+4b﹣3c=10x+28x﹣24x=14x=14.
故答案为:14.
13.已知点A(﹣1,y1),B(2,y2)在反比例函数y=(k<0)的图象上,则y1 y2(填“>”“<”或“=”)
【分析】先根据反比例函数的性质判断出函数图象所在的象限,再判断出在每一象限内的增减性,根据点A(﹣1,y1),B(2,y2)即可得出结论.
【解答】解:∵反比例函数y=中,k<0,
∴此函数的图象在二四象限,
∵A(﹣1,y1),B(2,y2),
∴点A在第二象限,点B在第四象限,
∴y1>0,y2<0,
∴y1>y2.
故答案为:>.
14.已知抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,则b的值为 .
【分析】根据(﹣2,n)和(4,n)可以确定函数的对称轴x=1,再由对称轴的x=即可求解;
【解答】解:抛物线y=﹣x2+bx+4经过(﹣2,n)和(4,n)两点,
可知函数的对称轴x=1,
∴=1,
∴b=2;
故答案为2.
15.当﹣4≤x≤2时,函数y=﹣x2﹣6x﹣7的取值范围为 .
【分析】先根据a=﹣1判断出抛物线的开口向下,故有最大值,可知对称轴x=﹣3,再根据﹣4≤x≤2,可知当x=﹣3时y最大,把x=2时y最小代入即可得出结论.
【解答】解:∵a=﹣1,
∴抛物线的开口向下,故有最大值,
∵对称轴x=﹣3,
∴当x=﹣3时y最大为2,
当x=2时y最小为﹣23,
∴函数y的取值范围为﹣23≤y≤2,
故答案为﹣23≤y≤2.
16.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k= .
【分析】首先根据反比例函数与正比例函数的图象特征,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于4,然后由反比例函数y=的比例系数k的几何意义,可知△AOC的面积等于|k|,从而求出k的值.
【解答】解:∵反比例函数与正比例函数的图象相交于A、B两点,
∴A、B两点关于原点对称,
∴OA=OB,
∴△BOC的面积=△AOC的面积=8÷2=4,
又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,
∴△AOC的面积=|k|,
∴|k|=4,
∵k>0,
∴k=8.
故答案为8.
17.如图,在△ABC中,AB=6,BC=8,AC=7,点D,E分别在AB,BC上,将△BDE沿ED折叠,点B的对应点F刚好落在AC上.当△CEF与△ABC相似时,BE的长为 .
【分析】根据折叠的性质得到BE=EF,根据相似三角形的性质即可得到结论.
【解答】解:∵将△BDE沿DE翻折得到△FDE,
∴BE=EF,
∵BC=8,
∴CE=8﹣BE,
当△CEF与△ABC相似时,=或=,即=或=,
解得:BE=或,
故答案是:或.
18.在直角坐标系中,点A的坐标为(3,0),若抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,则n的取值范围为 .
【分析】根据题意可以将函数解析式化为顶点式,由抛物线y=x2﹣2x+n﹣1与线段OA有且只有一个公共点,可以得到顶点的纵坐标为0或当x=0时y<0且当x=3时,y不小于0,从而可以求得x的取值范围.
【解答】解:∵点A的坐标为(3,0),抛物线y=x2﹣2x+n﹣1=(x﹣1)2+n﹣2与线段OA有且只有一个公共点,
∴n﹣2=0或,
解得,﹣2≤n<1或n=2,
故答案为:﹣2≤n<1或n=2.
解答题(共6小题,46分)
19.(6分)如图,a∥b∥c.直线m、n与a、b、c分别相交于点A、B、C和点D、E、F.
若AB:BC=2:5,DF=10,求EF的长.
【分析】根据平行线分线段成比例定理得到,然后利用比例性质求EF即可.
【解答】解:∵a∥b∥c,
∴,
∴,
解得.
20.(6分)如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
【分析】根据已知得出∠C=∠ADE,进而利用相似三角形的判定方法得出答案.
【解答】证明:∵AD=DB,
∴∠B=∠BAD.
∵∠BDA=∠1+∠C=∠2+∠ADE,
又∵∠1=∠2,
∴∠C=∠ADE.
∴△ABC∽△EAD.
21.(8分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于A(﹣2,1),B(1,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)求△AOB的面积;
(3)根据所给条件,请直接写出不等式kx+b<的解集.
【分析】(1)把点A(﹣2,1)代入反比例函数y=,得到关于m的一元一次方程,解之,得到m的值,即可得到反比例函数的解析式,把点B(1,n)代入反比例函数y=﹣得到关于n的一元一次方程,解之,即可得到n的值,得到点A和点B的坐标,利用待定系数法,解之,即可得到k和b的值,即可得到一次函数的表达式,
(2)把y=0代入一次函数y=﹣x﹣1,解之,得到点C的横坐标,根据点A和点B的纵坐标,分别求出△OAC和△OBC的面积,二者相加即可得到答案,
(3)根据函数图象,结合点A和点B的横坐标,即可得到答案.
【解答】解:(1)把点A(﹣2,1)代入反比例函数y=得:
1=,
解得:m=﹣2,
即反比例函数的解析式为:y=﹣,
把点B(1,n)代入反比例函数y=﹣得:
n=﹣2,
即点A的坐标为:(﹣2,1),点B的坐标为:(1,﹣2),
把点A(﹣2,1)和点B(1,﹣2)代入一次函数y=kx+b得:
,
解得:,
即一次函数的表达式为:y=﹣x﹣1,
(2)把y=0代入一次函数y=﹣x﹣1得:
﹣x﹣1=0,
解得:x=﹣1,
即点C的坐标为:(﹣1,0),OC的长为1,
点A到OC的距离为1,点B到OC的距离为2,
S△AOB=S△OAC+S△OBC
=+
=,
(3)如图可知:kx+b<的解集为:﹣2<x<0,x>1.
22.(8分)如图△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,
(1)求证:AD2=AC DC;
(2)若AC=a,求AD.
【分析】(1)根据两角对应相等证明△BCD∽△ABC,再根据相似三角形的性质即可得到;
(2)结合(1)的结论和已知条件可以得到关于x的方程,从而求解.
【解答】(1)证明:∵∠ABC=∠C=∠BDC,
∴△BCD∽△ABC.
∴,
又BC=BD=AD,
∴AD2=AC DC.
(2)解:∵AD2=AC DC,设AD=x,AC=AD+CD,
∴AD2=(AC-AD) AC,
x2=(a-x)a,
x(a+x)=a2,
x2+ax﹣a2=0,
x= (负值舍去).
即x= .
23.(9分)某社区决定把一块长50m,宽30m的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于14m,算出x≤18.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
【分析】(1)根据“活动区的面积=矩形空地面积﹣阴影区域面积”列出函数解析式便可,图形可得结论;
(2)根据题意可得y与x的关系式;
(3)根据二次函数的增减性及解一元二次方程可得结论;
【解答】解:(1)根据题意,绿化区的宽为:[30﹣(50﹣2x)]÷2=x﹣10
∴y=50×30﹣4x(x﹣10)=﹣4x2+40x+1500,
∵4个出口宽度相同,其宽度不小于14m,不大于26m,
∴12≤x≤18,
∴y=﹣4x2+40x+1500(12≤x≤18);
(2)y=﹣4x2+40x+1500=﹣4(x﹣5)2+1600,
∵a=﹣4<0,抛物线的开口向下,当12≤x≤18时,y随x的增大而减小,
∴当x=12时,y最大=1404,
答:活动区的最大面积为1404m2.
(3)设投资费用为w元,
由题意得,w=50(﹣4x2+40x+1500)+40×4x(x﹣10)=﹣40(x﹣5)2+76000,
∴当w=72000时,解得:x1=﹣5(不符合题意舍去),x2=15,
∵a=﹣40<0,
∴当x≥15时,w≤72000,
又∵12≤x≤18,
∴15≤x≤18,
∴当x=18时,投资费用最少,此时出口宽度为50﹣2x=50﹣2×18=14(m),
答:投资最少时活动区的出口宽度为14m.
24.(9分)如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
【分析】(1)利用待定系数法求解可得;
(2)利用待定系数法确定直线BC的解析式为y=﹣x+5,设D(x,﹣x2+4x+5),则E(x,﹣x+5),F(x,0),(0<x<5),则DE=﹣x2+5x,EF=﹣x+5,利用三角形的面积公式进行讨论:当DE:EF=2:3时,S△BDE:S△BEF=2:3;当DE:EF=3:2时,S△BDE:S△BEF=3:2,从而可得到关于x的方程,然后解方程求出x就看得到对应的D点坐标;
(3)先确定抛物线的对称轴,如图,设M(2,t),利用两点间的距离公式得到BC2=50,MC2=t2﹣10t+29,MB2=t2+9,利用勾股定理的逆定理分类讨论:当BC2+MC2=MB2时,△BCM为直角三角形,则50+t2﹣10t+29=t2+9;当BC2+MB2=MC2时,△BCM为直角三角形,则50+t2+9=t2﹣10t+29;当MC2+MB2=BC2时,△BCM为直角三角形,则t2﹣10t+29+t2+9=50,然后分别解关于t的方程,从而可得到满足条件的M点坐标.
【解答】解:(1)将A(﹣1,0),B(5,0)代入y=ax2+bx+5,
得:,
解得,
则抛物线解析式为y=﹣x2+4x+5;
(2)能.
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得,
解得,
所以直线BC的解析式为y=﹣x+5,
设D(x,﹣x2+4x+5),则E(x,﹣x+5),F(x,0),(0<x<5),
∴DE=﹣x2+4x+5﹣(﹣x+5)=﹣x2+5x,EF=﹣x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(﹣x2+5x):(﹣x+5)=2:3,
整理得3x2﹣17x+10=0,
解得x1=,x2=5(舍去),此时D点坐标为(,);
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(﹣x2+5x):(﹣x+5)=3:2,
整理得2x2﹣13x+15=0,
解得x1=,x2=5(舍去),此时D点坐标为(,);
综上所述,当点D的坐标为(,)或(,)时,直线BC把△BDF分成面积之比为2:3的两部分;
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t﹣5)2=t2﹣10t+29,MB2=(2﹣5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2﹣10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2﹣10t+29,解得t=﹣3,此时M点的坐标为(2,﹣3);
当MC2+MB2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2﹣10t+29+t2+9=50,解得t1=6,t2=﹣1,此时M点的坐标为(2,6)或(2,﹣1),
综上所述,满足条件的M点的坐标为(2,7),(2,﹣3),(2,6),(2,﹣1).
同课章节目录
