2021-2022学年人教版数学七年级上册4.2.1直线、射线、线段的概念 课件(28张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级上册4.2.1直线、射线、线段的概念 课件(28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
2.通过具体情境以及操作活动,了解两点确定一条直线.
1.通过动画演示和现实情境中理解线段、射线、直线,并知道它们的联系和区别.
3.通过探究活动,熟练掌握直线、射线、线段的表示方法.
4.试着描述简单的点和直线的位置关系。
目标展示,心中有数
观看动画并思考以下问题:
1.你觉得金箍棒神奇吗?由它的变化,你能想到我们小学学过的哪些线?
2.你能找一找生活中近似这些线的实例吗?
3.你是怎样区分它们的?
创设情境,问题导入
生活情景
烟花、 手电筒或探照灯等射出来的光线,都可以看作射线。
直线
知识点1
思考 经过一点画直线,能画几条?经过两点呢?动手试一试.
点我们通常用一个大写字母表示.
合作研讨,产生新知
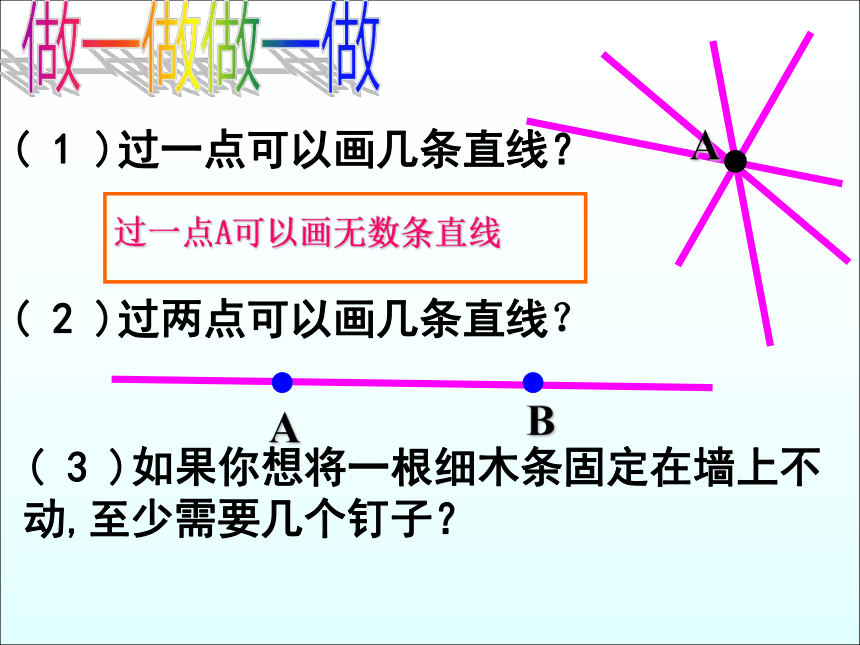
( 1 )过一点可以画几条直线?
( 2 )过两点可以画几条直线?
( 3 )如果你想将一根细木条固定在墙上不动,至少需要几个钉子?
过一点A可以画无数条直线
A
.
A
B
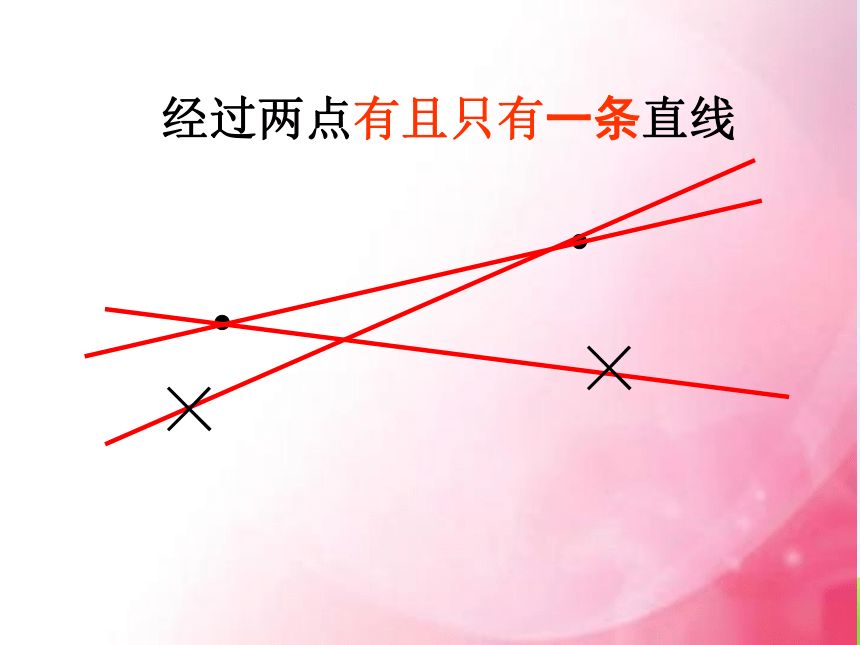
经过两点有且只有一条直线
×
×
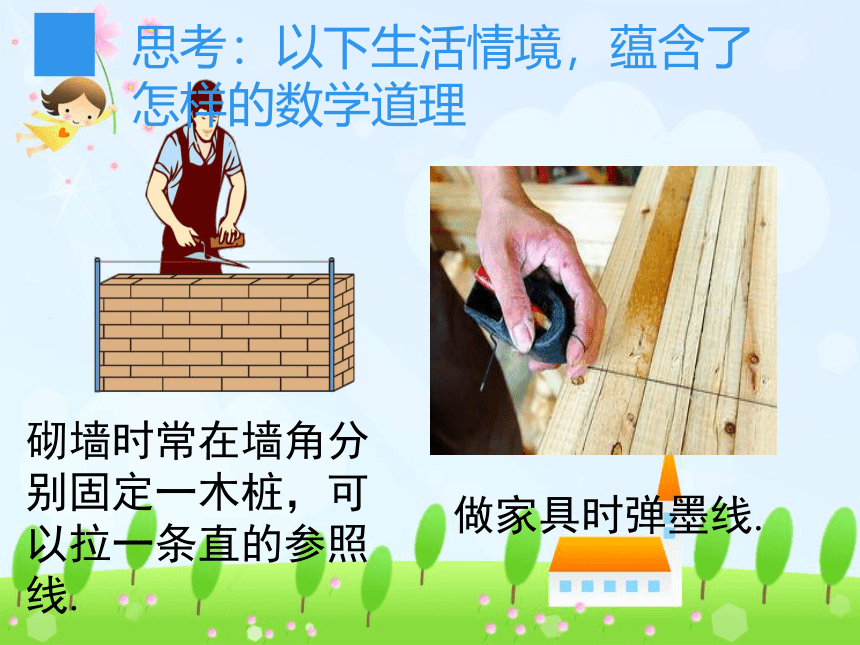
砌墙时常在墙角分别固定一木桩,可以拉一条直的参照线.
做家具时弹墨线.
思考:以下生活情境,蕴含了怎样的数学道理
经过两点有且只有一条直线
存在性
唯一性
直线的公理:
即:两点确定一条直线
思考 :我们应该如何表示一条直线?
读作:直线AB或直线BA,因为“两点确定一条直线”。
A
B
可以用小写字母表示,如直线l。
l
1
2
直线、射线、线段的表示方法
读作:射线AB
A
B
注意:①表示端点的字母写在首位;
② 两个字母不能调换位置.
A
B
读作:线段AB或线段BA
a
读作:线段a
你发现直线、射线、线段有什么联系吗?又有什么区别呢?
联系:都是直的,线段向一个方向延长可以得到射线, 线段向两个方向延长可以得到直线。由此可知, 射线、线段都是直线的一部分,线段是射线的一部分。
名称 图 形 表示方法 延伸性 端点 长度
线段
射线
直线
线段AB(或BA)
线段a
射线OM
直线AB
(或BA)
直线 m
不向任何
一方延伸
向一方
无限延伸
向两方
无限延伸
2
1
0
有
无
无
A
B
a
O
M
B
A
m
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
A
B
记作:直线AB ( )
√
A
B
记作:线段BA ( )
√
植树时,只要确定出两个树坑的位置就能确定同一行的树坑所在的直线.说明蕴含了怎样的数学道理
尝试练习
A
m
探究
两条直线相交只有一个交点。
图中直线 与直线m有一个公共点时,我们就称这两条直线相交于点A或这两条直线都经过点A(点A都在直线 和直线m上),这个公共点叫做它们的交点。
A
m
试着描述下图中点与直线的位置关系.
a
点 O 在直线 l 上;点 P不在直线 l 上或 点P在直线l 外.
l
b
直线 l 经过点 O;直线 l 不经过点 P.
·
O
·
P
自主探究,初步应用
1、判断:正确的打√,错的打×。
1、线段是直线的一部分。( )
2、一条射线长5000米。( )
3、一条射线上只有一个点,一条线段上有两个点。( )
4、直线AB与直线BA不是同一条直线。 ( )
√
×
课堂检测,及时反馈
×
×
2.指出下图中线段、射线、直线分别有多少条?
答:
有3条线段:线段AB、线段AC、线段BC.
有6条射线
只有1条直线:直线AB
A
B
C
重庆
永川
隆昌
资阳
成都
答:10种
往返重庆、成都两地的汽车,中途需要停靠永川、隆昌、资阳三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
A B C D E
变式训练,拓展延伸
数学问题
实际问题
转 化 为
课后反思,查漏补缺
1.挑战:你能用线段、射线或直线创造出美丽的图案吗?
2.完成P126第1和3题和相应课时练。
2.通过具体情境以及操作活动,了解两点确定一条直线.
1.通过动画演示和现实情境中理解线段、射线、直线,并知道它们的联系和区别.
3.通过探究活动,熟练掌握直线、射线、线段的表示方法.
4.试着描述简单的点和直线的位置关系。
目标展示,心中有数
观看动画并思考以下问题:
1.你觉得金箍棒神奇吗?由它的变化,你能想到我们小学学过的哪些线?
2.你能找一找生活中近似这些线的实例吗?
3.你是怎样区分它们的?
创设情境,问题导入
生活情景
烟花、 手电筒或探照灯等射出来的光线,都可以看作射线。
直线
知识点1
思考 经过一点画直线,能画几条?经过两点呢?动手试一试.
点我们通常用一个大写字母表示.
合作研讨,产生新知
( 1 )过一点可以画几条直线?
( 2 )过两点可以画几条直线?
( 3 )如果你想将一根细木条固定在墙上不动,至少需要几个钉子?
过一点A可以画无数条直线
A
.
A
B
经过两点有且只有一条直线
×
×
砌墙时常在墙角分别固定一木桩,可以拉一条直的参照线.
做家具时弹墨线.
思考:以下生活情境,蕴含了怎样的数学道理
经过两点有且只有一条直线
存在性
唯一性
直线的公理:
即:两点确定一条直线
思考 :我们应该如何表示一条直线?
读作:直线AB或直线BA,因为“两点确定一条直线”。
A
B
可以用小写字母表示,如直线l。
l
1
2
直线、射线、线段的表示方法
读作:射线AB
A
B
注意:①表示端点的字母写在首位;
② 两个字母不能调换位置.
A
B
读作:线段AB或线段BA
a
读作:线段a
你发现直线、射线、线段有什么联系吗?又有什么区别呢?
联系:都是直的,线段向一个方向延长可以得到射线, 线段向两个方向延长可以得到直线。由此可知, 射线、线段都是直线的一部分,线段是射线的一部分。
名称 图 形 表示方法 延伸性 端点 长度
线段
射线
直线
线段AB(或BA)
线段a
射线OM
直线AB
(或BA)
直线 m
不向任何
一方延伸
向一方
无限延伸
向两方
无限延伸
2
1
0
有
无
无
A
B
a
O
M
B
A
m
P
O
记作:射线PO ( )
a
b
记作:直线ab ( )
1
2
3
4
×
×
A
B
记作:直线AB ( )
√
A
B
记作:线段BA ( )
√
植树时,只要确定出两个树坑的位置就能确定同一行的树坑所在的直线.说明蕴含了怎样的数学道理
尝试练习
A
m
探究
两条直线相交只有一个交点。
图中直线 与直线m有一个公共点时,我们就称这两条直线相交于点A或这两条直线都经过点A(点A都在直线 和直线m上),这个公共点叫做它们的交点。
A
m
试着描述下图中点与直线的位置关系.
a
点 O 在直线 l 上;点 P不在直线 l 上或 点P在直线l 外.
l
b
直线 l 经过点 O;直线 l 不经过点 P.
·
O
·
P
自主探究,初步应用
1、判断:正确的打√,错的打×。
1、线段是直线的一部分。( )
2、一条射线长5000米。( )
3、一条射线上只有一个点,一条线段上有两个点。( )
4、直线AB与直线BA不是同一条直线。 ( )
√
×
课堂检测,及时反馈
×
×
2.指出下图中线段、射线、直线分别有多少条?
答:
有3条线段:线段AB、线段AC、线段BC.
有6条射线
只有1条直线:直线AB
A
B
C
重庆
永川
隆昌
资阳
成都
答:10种
往返重庆、成都两地的汽车,中途需要停靠永川、隆昌、资阳三个站点,根据你所学的知识回答: 需要制定多少种不同的票价?
A B C D E
变式训练,拓展延伸
数学问题
实际问题
转 化 为
课后反思,查漏补缺
1.挑战:你能用线段、射线或直线创造出美丽的图案吗?
2.完成P126第1和3题和相应课时练。
