2021-2022学年湘教新版九年级上册数学期中复习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版九年级上册数学期中复习试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 343.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 08:50:39 | ||
图片预览




文档简介
2021-2022学年湘教新版九年级上册数学期中复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.若是反比例函数,则m满足的条件是( )
A.m≠0 B.m=3 C.m=3或m=0 D.m≠3且m≠0
2.用放大镜观察一个五边形时,不变的量是( )
A.各边的长度 B.各内角的度数
C.五边形的周长 D.五边形的面积
3.用配方法解方程x2﹣2x﹣1=0,配方后所得方程为( )
A.(x+1)2=0 B.(x﹣1)2=0 C.(x+1)2=2 D.(x﹣1)2=2
4.已知函数y=的图象经过点(2,3),下列说法正确的是( )
A.y随x的增大而增大
B.当x<0时,必有y<0
C.函数的图象只在第一象限
D.点(﹣2,﹣3)不在此函数的图象上
5.已知:(a≠0),则的值为( )
A.3 B.2 C. D.
6.在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
A.﹣1 B.1 C.2 D.3
7.某县为发展教育事业,加强了对教育经费的投入,2008年投入3000万元,预计2010年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
A.3000(1+x)2=5000
B.3000x2=5000
C.3000(1+x%)2=5000
D.3000(1+x)+3000(1+x)2=5000
8.如图,在△ABC中,DE∥BC,AD:DB=2:3,若△ADE的周长为2a,则△ABC的周长是( )
A.3a B.9a C.5a D.25a
9.已知关于x的一元二次方程ax2﹣4x﹣1=0有两个不相等的实数根,则a的取值范围是( )
A.a≥﹣4 B.a>﹣4 C.a≥﹣4且a≠0 D.a>﹣4且a≠0
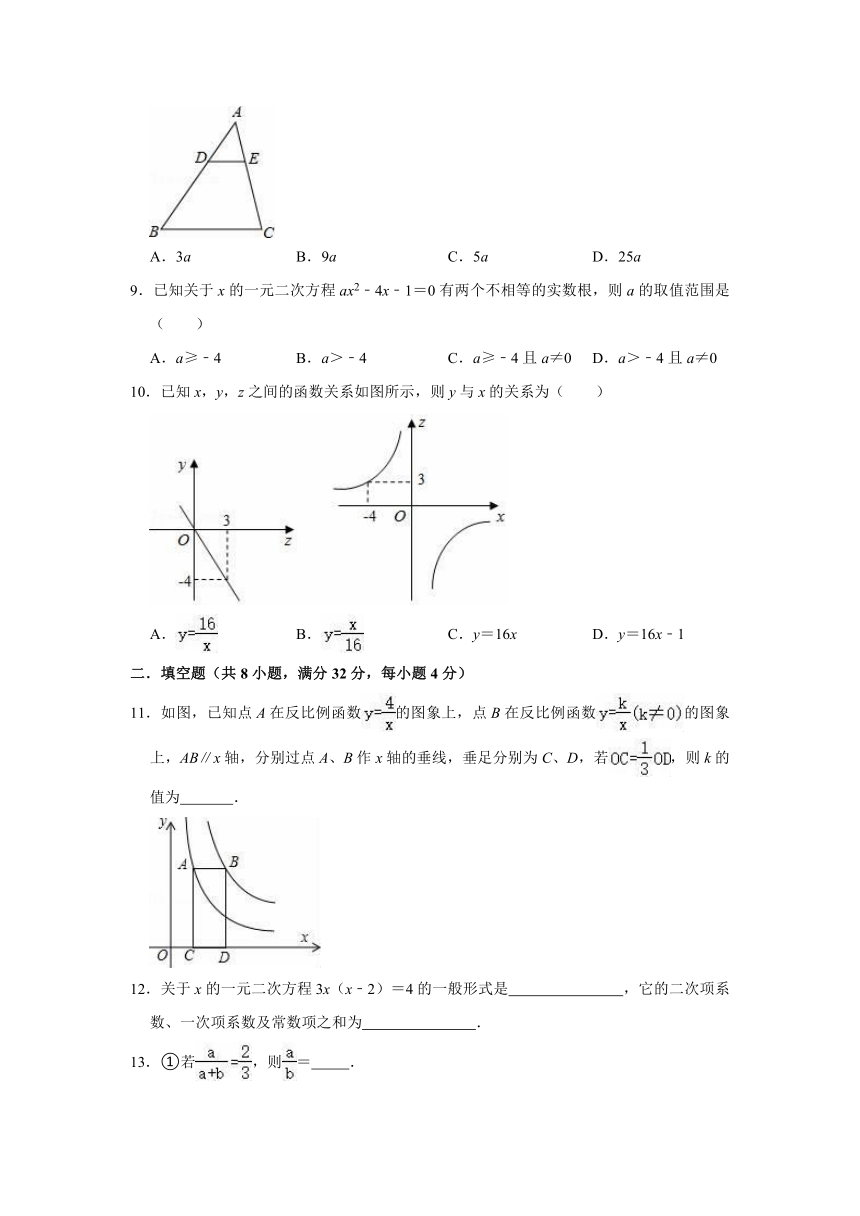
10.已知x,y,z之间的函数关系如图所示,则y与x的关系为( )
A. B. C.y=16x D.y=16x﹣1
二.填空题(共8小题,满分32分,每小题4分)
11.如图,已知点A在反比例函数的图象上,点B在反比例函数的图象上,AB∥x轴,分别过点A、B作x轴的垂线,垂足分别为C、D,若,则k的值为 .
12.关于x的一元二次方程3x(x﹣2)=4的一般形式是 ,它的二次项系数、一次项系数及常数项之和为 .
13.①若,则= .
②已知==,则的值为 .
14.对于反比例函数y=,当2≤x≤3时,y的最大值为﹣2,则当x≤1时,y的取值范围是 .
15.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成,定义=ad﹣bc,上述记号就叫做2阶行列式.若=17,则x= .
16.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 cm.
17.已知反比例函数的表达式为y=,它的图象在各自象限内具有y随x的增大而增大的特点,则k的取值范围是 .
18.如图,已知一次函数y=ax+b和反比例函数y=的图象相交于A(﹣2,y1)、B(1,y2)两点,则不等式ax+b<的解集为 .
三.解答题(共8小题,满分78分)
19.(8分)解方程:
(1)x2+2x﹣1=0
(2)(x﹣1)2=3(x﹣1)
20.(8分)小欣在学习了反比例函数的图象与性质后,进一步研究了函数y=的图象与性质.其研究过程如下:
(1)绘制函数图象
①列表:如表是x与y的几组对应值,其中m= ;
x … ﹣4 ﹣3 ﹣2 ﹣ ﹣ ﹣ ﹣ 0 1 2 …
y … ﹣ ﹣ ﹣1 ﹣2 ﹣3 3 2 m …
②描点:根据表中的数值描点(x,y),请补充描出点(0,m);
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
(2)探究函数性质
判断下列说法是否正确(正确的填“√”,错误的填“×”)
①函数值y随x的增大而减小: .
②函数图象关于原点对称: .
③函数图象与直线x=﹣1没有交点: .
21.(8分)已知a:b=3:2,求:
(1);
(2)的值.
22.(10分)已知关于x的一元二次方程x2+ax+a﹣2=0.
(1)若该方程的一个根为﹣2,求a的值及该方程的另一根;
(2)求证:无论a取何实数,该方程都有两个不相等的实数根.
23.(10分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(﹣2,﹣5)C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
24.(10分)今年我国发生了较为严重的新冠肺炎疫情,口罩供不应求,某商店恰好年前新进了一批口罩,若按每个盈利1元销售,每天可售出200个,如果每个口罩的售价上涨0.5元,则销售量就减少10个,问应将每个口罩涨价多少元时,才能让顾客得到实惠的同时每天利润为480元?
25.(12分)如图,在△ABC中,∠B=90°,AB=12cm,BC=16cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为t秒.
(1)当t为何值时,△PBQ的面积等于35cm2?
(2)当t为何值时,PQ的长度等于8cm?
(3)若点P,Q的速度保持不变,点P在到达点B后返回点A,点Q在到达点C后返回点B,一个点停止,另一个点也随之停止.问:当t为何值时,△PBQ的面积等于32cm2?
26.(12分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:由题意得:m(m﹣3)≠0,
解得:m≠0且m≠3,
故选:D.
2.解:∵用一个放大镜去观察一个五边形,
∴放大后的五边形与原五边形相似,
∵相似五边形的对应边成比例,
∴各边长都变大,故A选项错误;
∵相似五边形的对应角相等,
∴对应角大小不变,故选项B正确;
∵相似五边形的周长得比等于相似比,
∴C选项错误.
∵相似五边形的面积比等于相似比的平方,
∴D选项错误;
故选:B.
3.解:x2﹣2x=1,
x2﹣2x+1=2,
(x﹣1)2=2.
故选:D.
4.解:把(2,3)代入y=,解得k=6>0,
∴函数图象过一三象限,且在同一象限内y随x的增大而减小.
A、错误;
B、当x<0,必有y<0,正确;
C、错误;
D、点(﹣2,﹣3)代入函数式,成立,故在函数图象上,错误.
故选:B.
5.解:∵(a≠0),
∴,
∴=(1+)=×(1+)=;
故选:C.
6.解:∵反比例函数图象的每一条曲线上,y随x的增大而减小,
∴1﹣k>0,
解得k<1.
故选:A.
7.解:设教育经费的年平均增长率为x,
则2009的教育经费为:3000×(1+x)
2010的教育经费为:3000×(1+x)2.
那么可得方程:3000×(1+x)2=5000
故选:A.
8.解:∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴C△ABC=×2a=5a,
故选:C.
9.解:根据题意得a≠0且Δ=(﹣4)2﹣4a×(﹣1)>0,
解得a>﹣4且a≠0,
故选:D.
10.解:由图象可知,y是z的正比例函数,z是x的反比例函数,
设y=kz,z=,则y=,
∵函数y=kz过点(3,﹣4),
∴﹣4=3k,解得k=﹣,
∵函数z=过点(﹣4,3),
∴3=,解得m=﹣12,
∴y=,
故选:A.
二.填空题(共8小题,满分32分,每小题4分)
11.解:设A(a,b),
∵点A在反比例函数的图象上,
∴ab=4,
∵OC=a,OC=OD,
∴OD=3a,
∴B(3a,b),
∵点B在反比例函数的图象上,
∴k=3ab=3×4=12,
故答案为:12.
12.解:3x2﹣6x=4,
3x2﹣6x﹣4=0,
所以,一般形式是3x2﹣6x﹣4=0,二次项系数是3,一次项系数是﹣6,常数项是﹣4,
它的二次项系数、一次项系数及常数项之和为3﹣6﹣4=﹣7.
故答案为:3x2﹣6x﹣4=0,﹣7.
13.解:①设a=2k,则a+b=3k,
∴b=k,
∴==2;
故答案为:2;
②设x=2k,y=7k,z=5k,
∴===2.
故答案为:2.
14.解:∵对于反比例函数y=,当2≤x≤3时,y的最大值为﹣2,
∴k<0,
∴在函数图象所在的每一象限内,y随x的增大而增大,
∴当x=3时,y=﹣2,
∴k=﹣6,
∴当x=1时,y=﹣6,
∴当x≤1时,y≤﹣6或y>0,
故答案为:y≤﹣6或y>0.
15.解:由题意可得:
(x+1)2﹣(x+2)(x﹣2)=17,
x2+2x+1﹣(x2﹣4)=17,
x2+2x+1﹣x2+4=17,
2x=12,
x=6,
故答案为:6.
16.解:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x﹣2=0或x﹣1=0,
∴x1=2,x2=1,
当x=2时,三角形三边为3,2,2,则三角形的周长=3+2+2=7(cm);
当x=1时,由于1+2=3,不符合三角形三边的关系,舍去.
所以这个三角形的周长为7cm,
故答案为7.
17.解:∵反比例函数y=图象在每个象限内y的值随x的值增大而大,
∴k+2<0,
解得k<﹣2.
故答案为k<﹣2.
18.解:观察函数图象,发现:当﹣2<x<0或x>1时,一次函数图象在反比例函数图象的下方,
则不等式ax+b<的解集是﹣2<x<0或x>1.
故答案为:﹣2<x<0或x>1.
三.解答题(共8小题,满分78分)
19.解:(1)∵x2+2x=1,
∴x2+2x+1=1+1,即(x+1)2=2,
∴x+1=±,
则x=﹣1;
(2)∵(x﹣1)2﹣3(x﹣1)=0,
∴(x﹣1)(x﹣4)=0,
则x﹣1=0或x﹣4=0,
解得x=1或x=4.
20.解:(1)①x=0时,y==1,
故答案为:1;
②如图:
∵m=1,
∴A即为(0,m)的点;
③补充图象如图:
(2)根据函数图象可得:
①每一个分支上,函数值y随x的增大而减小,故①错误,应为×,
②图象关于(﹣1,0)对称,故②错误,应为×,
③x=﹣1时,无意义,函数图象与直线x=﹣1没有交点,应为√.
故答案为:×,×,√.
21.解:∵a:b=3:2,
∴设a=3k,b=2k,
(1)==;
(2)==﹣1.
22.解:(1)将x=﹣2代入方程x2+ax+a﹣2=0得,4﹣2a+a﹣2=0,
解得,a=2;
方程为x2+2x=0,解得x1=0,x2=﹣2,
即方程的另一根为0;
(2)∵Δ=a2﹣4(a﹣2)=a2﹣4a+8=a2﹣4a+4+4=(a﹣2)2+4>0,
∴不论a取何实数,该方程都有两个不相等的实数根.
23.解:(1)把A(﹣2,﹣5)代入y=得:﹣5=,
解得:m=10,
则反比例函数的解析式是:y=,
把x=5代入,得:y==2,
则C的坐标是(5,2).
根据题意得:,
解得:,
则一次函数的解析式是:y=x﹣3.
(2)在y=x﹣3中,令x=0,解得:y=﹣3.
则B的坐标是(0,﹣3).
∴OB=3,
∵点A的横坐标是﹣2,C的横坐标是5.
∴S△AOC=S△AOB+S△BOC=OB×2×5+×OB×5=×3×7=.
24.解:设应将每个口罩涨价x元,则每天可售出(200﹣10×)个,
依题意,得:(1+x)(200﹣10×)=480,
化简,得:x2﹣9x+14=0,
解得:x1=2,x2=7.
又∵要让顾客得到实惠,
∴x=2.
答:应将每个口罩涨价2元时,才能让顾客得到实惠的同时每天利润为480元.
25.解:根据题意知BP=AB﹣AP=12﹣t,BQ=2t.
(1)根据三角形的面积公式,得
PB BQ=35,
t(12﹣t)=35,
t2﹣12t+35=0,
解得t1=5,t2=7.
故当t为5或7时,△PBQ的面积等于35cm2.
(2)设t秒后,PQ的长度等于8cm,根据勾股定理,得
PQ2=BP2+BQ2=(12﹣t)2+(2t)2=128,
5t2﹣24t+16=0,
解得t1=,t2=4.
故当t为或4时,PQ的长度等于8cm.
(3)当0<t≤8时,
PB BQ=32,即×2t×(12﹣t)=32,
则t2﹣12t+32=0,
解得t1=4,t2=8.
当8<t≤12时,
则CQ=2t﹣16,BQ=BC﹣CQ=16﹣(2t﹣16)=32﹣2t,PB=12﹣t,
则△PBQ的面积=PB BQ=×(12﹣t)×(32﹣2t)=32,
解得:t=20或8(均舍去);
当12<t≤16时,
PB BQ=32,
(16﹣t)(t﹣12)=32,
t2﹣28t+224=0,
Δ=282﹣4×1×224=﹣112<0,
故方程无实数根.
综上所述,当t为4或8时,△PBQ的面积等于32cm2.
26.解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
一.选择题(共10小题,满分40分,每小题4分)
1.若是反比例函数,则m满足的条件是( )
A.m≠0 B.m=3 C.m=3或m=0 D.m≠3且m≠0
2.用放大镜观察一个五边形时,不变的量是( )
A.各边的长度 B.各内角的度数
C.五边形的周长 D.五边形的面积
3.用配方法解方程x2﹣2x﹣1=0,配方后所得方程为( )
A.(x+1)2=0 B.(x﹣1)2=0 C.(x+1)2=2 D.(x﹣1)2=2
4.已知函数y=的图象经过点(2,3),下列说法正确的是( )
A.y随x的增大而增大
B.当x<0时,必有y<0
C.函数的图象只在第一象限
D.点(﹣2,﹣3)不在此函数的图象上
5.已知:(a≠0),则的值为( )
A.3 B.2 C. D.
6.在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
A.﹣1 B.1 C.2 D.3
7.某县为发展教育事业,加强了对教育经费的投入,2008年投入3000万元,预计2010年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
A.3000(1+x)2=5000
B.3000x2=5000
C.3000(1+x%)2=5000
D.3000(1+x)+3000(1+x)2=5000
8.如图,在△ABC中,DE∥BC,AD:DB=2:3,若△ADE的周长为2a,则△ABC的周长是( )
A.3a B.9a C.5a D.25a
9.已知关于x的一元二次方程ax2﹣4x﹣1=0有两个不相等的实数根,则a的取值范围是( )
A.a≥﹣4 B.a>﹣4 C.a≥﹣4且a≠0 D.a>﹣4且a≠0
10.已知x,y,z之间的函数关系如图所示,则y与x的关系为( )
A. B. C.y=16x D.y=16x﹣1
二.填空题(共8小题,满分32分,每小题4分)
11.如图,已知点A在反比例函数的图象上,点B在反比例函数的图象上,AB∥x轴,分别过点A、B作x轴的垂线,垂足分别为C、D,若,则k的值为 .
12.关于x的一元二次方程3x(x﹣2)=4的一般形式是 ,它的二次项系数、一次项系数及常数项之和为 .
13.①若,则= .
②已知==,则的值为 .
14.对于反比例函数y=,当2≤x≤3时,y的最大值为﹣2,则当x≤1时,y的取值范围是 .
15.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成,定义=ad﹣bc,上述记号就叫做2阶行列式.若=17,则x= .
16.一个三角形的两边长分别是3cm和2cm,第三边的长为xcm,若x满足x2﹣3x+2=0,则这个三角形的周长为 cm.
17.已知反比例函数的表达式为y=,它的图象在各自象限内具有y随x的增大而增大的特点,则k的取值范围是 .
18.如图,已知一次函数y=ax+b和反比例函数y=的图象相交于A(﹣2,y1)、B(1,y2)两点,则不等式ax+b<的解集为 .
三.解答题(共8小题,满分78分)
19.(8分)解方程:
(1)x2+2x﹣1=0
(2)(x﹣1)2=3(x﹣1)
20.(8分)小欣在学习了反比例函数的图象与性质后,进一步研究了函数y=的图象与性质.其研究过程如下:
(1)绘制函数图象
①列表:如表是x与y的几组对应值,其中m= ;
x … ﹣4 ﹣3 ﹣2 ﹣ ﹣ ﹣ ﹣ 0 1 2 …
y … ﹣ ﹣ ﹣1 ﹣2 ﹣3 3 2 m …
②描点:根据表中的数值描点(x,y),请补充描出点(0,m);
③连线:用平滑的曲线顺次连接各点,请把图象补充完整.
(2)探究函数性质
判断下列说法是否正确(正确的填“√”,错误的填“×”)
①函数值y随x的增大而减小: .
②函数图象关于原点对称: .
③函数图象与直线x=﹣1没有交点: .
21.(8分)已知a:b=3:2,求:
(1);
(2)的值.
22.(10分)已知关于x的一元二次方程x2+ax+a﹣2=0.
(1)若该方程的一个根为﹣2,求a的值及该方程的另一根;
(2)求证:无论a取何实数,该方程都有两个不相等的实数根.
23.(10分)如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A(﹣2,﹣5)C(5,n),交y轴于点B,交x轴于点D.
(1)求反比例函数y=和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
24.(10分)今年我国发生了较为严重的新冠肺炎疫情,口罩供不应求,某商店恰好年前新进了一批口罩,若按每个盈利1元销售,每天可售出200个,如果每个口罩的售价上涨0.5元,则销售量就减少10个,问应将每个口罩涨价多少元时,才能让顾客得到实惠的同时每天利润为480元?
25.(12分)如图,在△ABC中,∠B=90°,AB=12cm,BC=16cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,当一个点到达终点时,另一个点也随之停止运动.设运动的时间为t秒.
(1)当t为何值时,△PBQ的面积等于35cm2?
(2)当t为何值时,PQ的长度等于8cm?
(3)若点P,Q的速度保持不变,点P在到达点B后返回点A,点Q在到达点C后返回点B,一个点停止,另一个点也随之停止.问:当t为何值时,△PBQ的面积等于32cm2?
26.(12分)如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:由题意得:m(m﹣3)≠0,
解得:m≠0且m≠3,
故选:D.
2.解:∵用一个放大镜去观察一个五边形,
∴放大后的五边形与原五边形相似,
∵相似五边形的对应边成比例,
∴各边长都变大,故A选项错误;
∵相似五边形的对应角相等,
∴对应角大小不变,故选项B正确;
∵相似五边形的周长得比等于相似比,
∴C选项错误.
∵相似五边形的面积比等于相似比的平方,
∴D选项错误;
故选:B.
3.解:x2﹣2x=1,
x2﹣2x+1=2,
(x﹣1)2=2.
故选:D.
4.解:把(2,3)代入y=,解得k=6>0,
∴函数图象过一三象限,且在同一象限内y随x的增大而减小.
A、错误;
B、当x<0,必有y<0,正确;
C、错误;
D、点(﹣2,﹣3)代入函数式,成立,故在函数图象上,错误.
故选:B.
5.解:∵(a≠0),
∴,
∴=(1+)=×(1+)=;
故选:C.
6.解:∵反比例函数图象的每一条曲线上,y随x的增大而减小,
∴1﹣k>0,
解得k<1.
故选:A.
7.解:设教育经费的年平均增长率为x,
则2009的教育经费为:3000×(1+x)
2010的教育经费为:3000×(1+x)2.
那么可得方程:3000×(1+x)2=5000
故选:A.
8.解:∵DE∥BC,
∴△ADE∽△ABC,
∴==,
∴C△ABC=×2a=5a,
故选:C.
9.解:根据题意得a≠0且Δ=(﹣4)2﹣4a×(﹣1)>0,
解得a>﹣4且a≠0,
故选:D.
10.解:由图象可知,y是z的正比例函数,z是x的反比例函数,
设y=kz,z=,则y=,
∵函数y=kz过点(3,﹣4),
∴﹣4=3k,解得k=﹣,
∵函数z=过点(﹣4,3),
∴3=,解得m=﹣12,
∴y=,
故选:A.
二.填空题(共8小题,满分32分,每小题4分)
11.解:设A(a,b),
∵点A在反比例函数的图象上,
∴ab=4,
∵OC=a,OC=OD,
∴OD=3a,
∴B(3a,b),
∵点B在反比例函数的图象上,
∴k=3ab=3×4=12,
故答案为:12.
12.解:3x2﹣6x=4,
3x2﹣6x﹣4=0,
所以,一般形式是3x2﹣6x﹣4=0,二次项系数是3,一次项系数是﹣6,常数项是﹣4,
它的二次项系数、一次项系数及常数项之和为3﹣6﹣4=﹣7.
故答案为:3x2﹣6x﹣4=0,﹣7.
13.解:①设a=2k,则a+b=3k,
∴b=k,
∴==2;
故答案为:2;
②设x=2k,y=7k,z=5k,
∴===2.
故答案为:2.
14.解:∵对于反比例函数y=,当2≤x≤3时,y的最大值为﹣2,
∴k<0,
∴在函数图象所在的每一象限内,y随x的增大而增大,
∴当x=3时,y=﹣2,
∴k=﹣6,
∴当x=1时,y=﹣6,
∴当x≤1时,y≤﹣6或y>0,
故答案为:y≤﹣6或y>0.
15.解:由题意可得:
(x+1)2﹣(x+2)(x﹣2)=17,
x2+2x+1﹣(x2﹣4)=17,
x2+2x+1﹣x2+4=17,
2x=12,
x=6,
故答案为:6.
16.解:x2﹣3x+2=0,
(x﹣2)(x﹣1)=0,
∴x﹣2=0或x﹣1=0,
∴x1=2,x2=1,
当x=2时,三角形三边为3,2,2,则三角形的周长=3+2+2=7(cm);
当x=1时,由于1+2=3,不符合三角形三边的关系,舍去.
所以这个三角形的周长为7cm,
故答案为7.
17.解:∵反比例函数y=图象在每个象限内y的值随x的值增大而大,
∴k+2<0,
解得k<﹣2.
故答案为k<﹣2.
18.解:观察函数图象,发现:当﹣2<x<0或x>1时,一次函数图象在反比例函数图象的下方,
则不等式ax+b<的解集是﹣2<x<0或x>1.
故答案为:﹣2<x<0或x>1.
三.解答题(共8小题,满分78分)
19.解:(1)∵x2+2x=1,
∴x2+2x+1=1+1,即(x+1)2=2,
∴x+1=±,
则x=﹣1;
(2)∵(x﹣1)2﹣3(x﹣1)=0,
∴(x﹣1)(x﹣4)=0,
则x﹣1=0或x﹣4=0,
解得x=1或x=4.
20.解:(1)①x=0时,y==1,
故答案为:1;
②如图:
∵m=1,
∴A即为(0,m)的点;
③补充图象如图:
(2)根据函数图象可得:
①每一个分支上,函数值y随x的增大而减小,故①错误,应为×,
②图象关于(﹣1,0)对称,故②错误,应为×,
③x=﹣1时,无意义,函数图象与直线x=﹣1没有交点,应为√.
故答案为:×,×,√.
21.解:∵a:b=3:2,
∴设a=3k,b=2k,
(1)==;
(2)==﹣1.
22.解:(1)将x=﹣2代入方程x2+ax+a﹣2=0得,4﹣2a+a﹣2=0,
解得,a=2;
方程为x2+2x=0,解得x1=0,x2=﹣2,
即方程的另一根为0;
(2)∵Δ=a2﹣4(a﹣2)=a2﹣4a+8=a2﹣4a+4+4=(a﹣2)2+4>0,
∴不论a取何实数,该方程都有两个不相等的实数根.
23.解:(1)把A(﹣2,﹣5)代入y=得:﹣5=,
解得:m=10,
则反比例函数的解析式是:y=,
把x=5代入,得:y==2,
则C的坐标是(5,2).
根据题意得:,
解得:,
则一次函数的解析式是:y=x﹣3.
(2)在y=x﹣3中,令x=0,解得:y=﹣3.
则B的坐标是(0,﹣3).
∴OB=3,
∵点A的横坐标是﹣2,C的横坐标是5.
∴S△AOC=S△AOB+S△BOC=OB×2×5+×OB×5=×3×7=.
24.解:设应将每个口罩涨价x元,则每天可售出(200﹣10×)个,
依题意,得:(1+x)(200﹣10×)=480,
化简,得:x2﹣9x+14=0,
解得:x1=2,x2=7.
又∵要让顾客得到实惠,
∴x=2.
答:应将每个口罩涨价2元时,才能让顾客得到实惠的同时每天利润为480元.
25.解:根据题意知BP=AB﹣AP=12﹣t,BQ=2t.
(1)根据三角形的面积公式,得
PB BQ=35,
t(12﹣t)=35,
t2﹣12t+35=0,
解得t1=5,t2=7.
故当t为5或7时,△PBQ的面积等于35cm2.
(2)设t秒后,PQ的长度等于8cm,根据勾股定理,得
PQ2=BP2+BQ2=(12﹣t)2+(2t)2=128,
5t2﹣24t+16=0,
解得t1=,t2=4.
故当t为或4时,PQ的长度等于8cm.
(3)当0<t≤8时,
PB BQ=32,即×2t×(12﹣t)=32,
则t2﹣12t+32=0,
解得t1=4,t2=8.
当8<t≤12时,
则CQ=2t﹣16,BQ=BC﹣CQ=16﹣(2t﹣16)=32﹣2t,PB=12﹣t,
则△PBQ的面积=PB BQ=×(12﹣t)×(32﹣2t)=32,
解得:t=20或8(均舍去);
当12<t≤16时,
PB BQ=32,
(16﹣t)(t﹣12)=32,
t2﹣28t+224=0,
Δ=282﹣4×1×224=﹣112<0,
故方程无实数根.
综上所述,当t为4或8时,△PBQ的面积等于32cm2.
26.解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
同课章节目录
