2011学年第一学期期中考试八年级数学试卷
文档属性
| 名称 | 2011学年第一学期期中考试八年级数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 72.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-09 22:27:25 | ||
图片预览


文档简介
2011学年第一学期六校期中考试八年级数学试卷
(考试时间90分钟,满分100分)
题号 一 二 三 四 五 总分
得分
选择题:(本大题共6题,每题3分,满分18分)
1.如果有意义,那么字母的取值范围是 ( )
A. B. C. D.
2.二次根式、、、中最简二次根式有 ( )
(A)1个 (B)2个 (C)3个 (D)4个
3.下列二次根式中,与是同类二次根式的是 ( )
(A) (B) (C) (D)
4.下列方程中是一元二次方程的是 ( )
(A) (B) (C) (D)
5.下列命题中,假命题是 ( )
(A)两直线平行,内错角相等;
(B)两个互为邻补角的角平分线互相垂直;
(C)互为补角的两个角都是锐角;
(D)在一个三角形中,等边对等角。
6.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是 ( )
(A) AH=BD (B)HE=EC
(C) △AHE≌△BHD (D) △ADC≌△BDH
二、填空题:(本大题共12题,每题2分,满分24分)
7.若,则的取值范围是 .
8.的倒数是 .
9.化简:= .
10.的有理化因式是 .
11.不等式的解集是 .
12. 方程的根是 .
13.关于的方程有实数根,则的取值范围是 .
14.在实数范围内分解因式:= .
15.请写出一个一元二次方程,使其二次项系数为2,有一个根1:___________.
16. 某件商品原价为100元,经过两次降价,且每次降价的百分率相同,现价为81元,则每次降价的百分率为 .
17. 命题“全等三角形的面积相等”的逆命题是
.
18.、 已知:如图,AB=AC,要使BD=CE,还需添加一个条件,这个条件可以是 .
三、(本大题共6题,每题6分,满分36分)
19计算 20.若,求的值
21.解方程 22.解方程(配方法)
23.已知三角形的两边长分别是3和8,第三边的数值是一元二次方程
的根,求此三角形的周长。
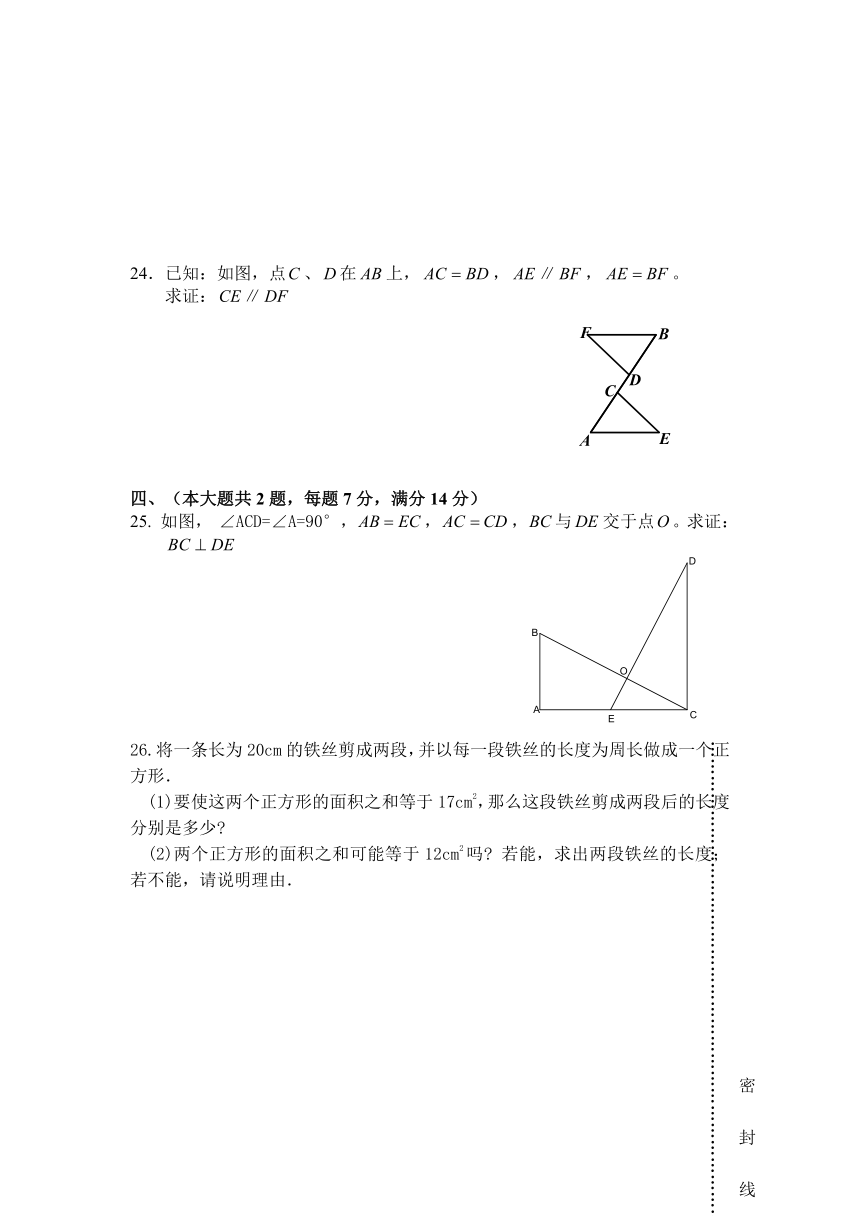
24.已知:如图,点、在上,,∥,。
求证:∥
四、(本大题共2题,每题7分,满分14分)
25. 如图, ∠ACD=∠A=90°,,,与交于点。求证:
26.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少
(2)两个正方形的面积之和可能等于12cm2吗 若能,求出两段铁丝的长度;若不能,请说明理由.
五、(本大题第(1)小题5分,第(2)小题3分,满分8分)
27.如图在ΔABC中AB=AC,∠BAC=900,P为边BC的中点,以点P为顶点的直角的两边PE、PF分别交边AB、AC于点E、F 。
(1)求证: BE=AF;
(2)当直角∠EPF绕点P旋转,(两边PE、PF仍然分别交边AB、AC于点E、F),四边形AEPF的面积是否改变?请说明理由。
2011学年第一学期六校期中八年级数学
参考答案及评分说明
(考试时间90分钟,满分100分)
选择题:(本大题共6题,每题3分,满分18分)
1、C 2、B 3、C 4、C 5、C 6、D
二、填空题:(本大题共12题,每题2分,满分24分)
7、 8、 9、 10、
11、> 12、 13、
14、 15、 等等
16、10% 17、面积相等的三角形是全等三角形 18、AE=AD 等等
三、(本大题共6题,每题6分,满分36分)
19、解:
= (3分)
= (3分)
20、解:
= (1分)
= (1分)
= (1分)
= (1分)
= (1分)
= (1分)
21、解:
(1分)
(1分)
(2分)
, (1分)
∴原方程的根是, (1分)
22、解:
(1分)
(1分)
(1分)
或 (1分)
或 (1分)
∴原方程的根是, (1分)
23、解:
(2分)
, (1分)
当时,三角形周长为 (1分)
当时,3+8=11,不可能构成三角形,舍去。 (1分)
∴这个三角形周长为17。 (1分)
24、证明:∵∥
∴∠B=∠A (1分)
证全等 (2分)
证 ∠BDF=∠ACE (1分)
证 ∠FDC=∠DCE (1分)
得 ∥ (1分)
四、(本大题共2题,每题7分,满分14分)
25、证明: 证△ABC≌△CED (2分)
得 ∠B=∠DEC (1分)
证 ∠B+∠BCA=90° (1分)
得 ∠DEC+∠BCA=90° (1分)
得 ∠COE=90° (1分)
即 (1分)
26、解:设做成的一个正方形的边长为cm,
则另一个正方形的边长为cm (1分)
(1) (2分)
, (1分)
则两段的长度分别为4cm,16cm。
答:这段铁丝剪成两段后的长度分别是4cm,16cm。
(2) (1分)
△=-4<0 (1分)
方程无实根。
∴两个正方形的面积之和不可能等于12cm2 (1分)
五、(本大题只有1题,第(1)小题5分,第(2)小题3分,满分8分)
27、(1)证明:联接AP
证 ∠B=∠C=45° (1分)
证 ∠BAP=∠PAC=45° AP⊥BC (1分)
证 AP=BP=PC (1分)
证 ∠BPE=∠APF (1分)
证全等,得BE=AF (1分)
(2) 解:不会改变。 (1分)
证 (2分)
学校_______________________ 班级__________ 学号_________ 姓名______________
……………………………………………密○………………………………………封○………………………………………○线…………………………
A
B
C
D
E
(第15题)
……………………………………………………………………………………………………………………………………………
密 封 线 内 不 准 答 题
P
F
E
C
B
A
(考试时间90分钟,满分100分)
题号 一 二 三 四 五 总分
得分
选择题:(本大题共6题,每题3分,满分18分)
1.如果有意义,那么字母的取值范围是 ( )
A. B. C. D.
2.二次根式、、、中最简二次根式有 ( )
(A)1个 (B)2个 (C)3个 (D)4个
3.下列二次根式中,与是同类二次根式的是 ( )
(A) (B) (C) (D)
4.下列方程中是一元二次方程的是 ( )
(A) (B) (C) (D)
5.下列命题中,假命题是 ( )
(A)两直线平行,内错角相等;
(B)两个互为邻补角的角平分线互相垂直;
(C)互为补角的两个角都是锐角;
(D)在一个三角形中,等边对等角。
6.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE交于H,且HD=DC,那么下列结论中正确的是 ( )
(A) AH=BD (B)HE=EC
(C) △AHE≌△BHD (D) △ADC≌△BDH
二、填空题:(本大题共12题,每题2分,满分24分)
7.若,则的取值范围是 .
8.的倒数是 .
9.化简:= .
10.的有理化因式是 .
11.不等式的解集是 .
12. 方程的根是 .
13.关于的方程有实数根,则的取值范围是 .
14.在实数范围内分解因式:= .
15.请写出一个一元二次方程,使其二次项系数为2,有一个根1:___________.
16. 某件商品原价为100元,经过两次降价,且每次降价的百分率相同,现价为81元,则每次降价的百分率为 .
17. 命题“全等三角形的面积相等”的逆命题是
.
18.、 已知:如图,AB=AC,要使BD=CE,还需添加一个条件,这个条件可以是 .
三、(本大题共6题,每题6分,满分36分)
19计算 20.若,求的值
21.解方程 22.解方程(配方法)
23.已知三角形的两边长分别是3和8,第三边的数值是一元二次方程
的根,求此三角形的周长。
24.已知:如图,点、在上,,∥,。
求证:∥
四、(本大题共2题,每题7分,满分14分)
25. 如图, ∠ACD=∠A=90°,,,与交于点。求证:
26.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于17cm2,那么这段铁丝剪成两段后的长度分别是多少
(2)两个正方形的面积之和可能等于12cm2吗 若能,求出两段铁丝的长度;若不能,请说明理由.
五、(本大题第(1)小题5分,第(2)小题3分,满分8分)
27.如图在ΔABC中AB=AC,∠BAC=900,P为边BC的中点,以点P为顶点的直角的两边PE、PF分别交边AB、AC于点E、F 。
(1)求证: BE=AF;
(2)当直角∠EPF绕点P旋转,(两边PE、PF仍然分别交边AB、AC于点E、F),四边形AEPF的面积是否改变?请说明理由。
2011学年第一学期六校期中八年级数学
参考答案及评分说明
(考试时间90分钟,满分100分)
选择题:(本大题共6题,每题3分,满分18分)
1、C 2、B 3、C 4、C 5、C 6、D
二、填空题:(本大题共12题,每题2分,满分24分)
7、 8、 9、 10、
11、> 12、 13、
14、 15、 等等
16、10% 17、面积相等的三角形是全等三角形 18、AE=AD 等等
三、(本大题共6题,每题6分,满分36分)
19、解:
= (3分)
= (3分)
20、解:
= (1分)
= (1分)
= (1分)
= (1分)
= (1分)
= (1分)
21、解:
(1分)
(1分)
(2分)
, (1分)
∴原方程的根是, (1分)
22、解:
(1分)
(1分)
(1分)
或 (1分)
或 (1分)
∴原方程的根是, (1分)
23、解:
(2分)
, (1分)
当时,三角形周长为 (1分)
当时,3+8=11,不可能构成三角形,舍去。 (1分)
∴这个三角形周长为17。 (1分)
24、证明:∵∥
∴∠B=∠A (1分)
证全等 (2分)
证 ∠BDF=∠ACE (1分)
证 ∠FDC=∠DCE (1分)
得 ∥ (1分)
四、(本大题共2题,每题7分,满分14分)
25、证明: 证△ABC≌△CED (2分)
得 ∠B=∠DEC (1分)
证 ∠B+∠BCA=90° (1分)
得 ∠DEC+∠BCA=90° (1分)
得 ∠COE=90° (1分)
即 (1分)
26、解:设做成的一个正方形的边长为cm,
则另一个正方形的边长为cm (1分)
(1) (2分)
, (1分)
则两段的长度分别为4cm,16cm。
答:这段铁丝剪成两段后的长度分别是4cm,16cm。
(2) (1分)
△=-4<0 (1分)
方程无实根。
∴两个正方形的面积之和不可能等于12cm2 (1分)
五、(本大题只有1题,第(1)小题5分,第(2)小题3分,满分8分)
27、(1)证明:联接AP
证 ∠B=∠C=45° (1分)
证 ∠BAP=∠PAC=45° AP⊥BC (1分)
证 AP=BP=PC (1分)
证 ∠BPE=∠APF (1分)
证全等,得BE=AF (1分)
(2) 解:不会改变。 (1分)
证 (2分)
学校_______________________ 班级__________ 学号_________ 姓名______________
……………………………………………密○………………………………………封○………………………………………○线…………………………
A
B
C
D
E
(第15题)
……………………………………………………………………………………………………………………………………………
密 封 线 内 不 准 答 题
P
F
E
C
B
A
同课章节目录
