冀教版七年级下册数学 期中达标测试卷(Word版 含答案)
文档属性
| 名称 | 冀教版七年级下册数学 期中达标测试卷(Word版 含答案) | 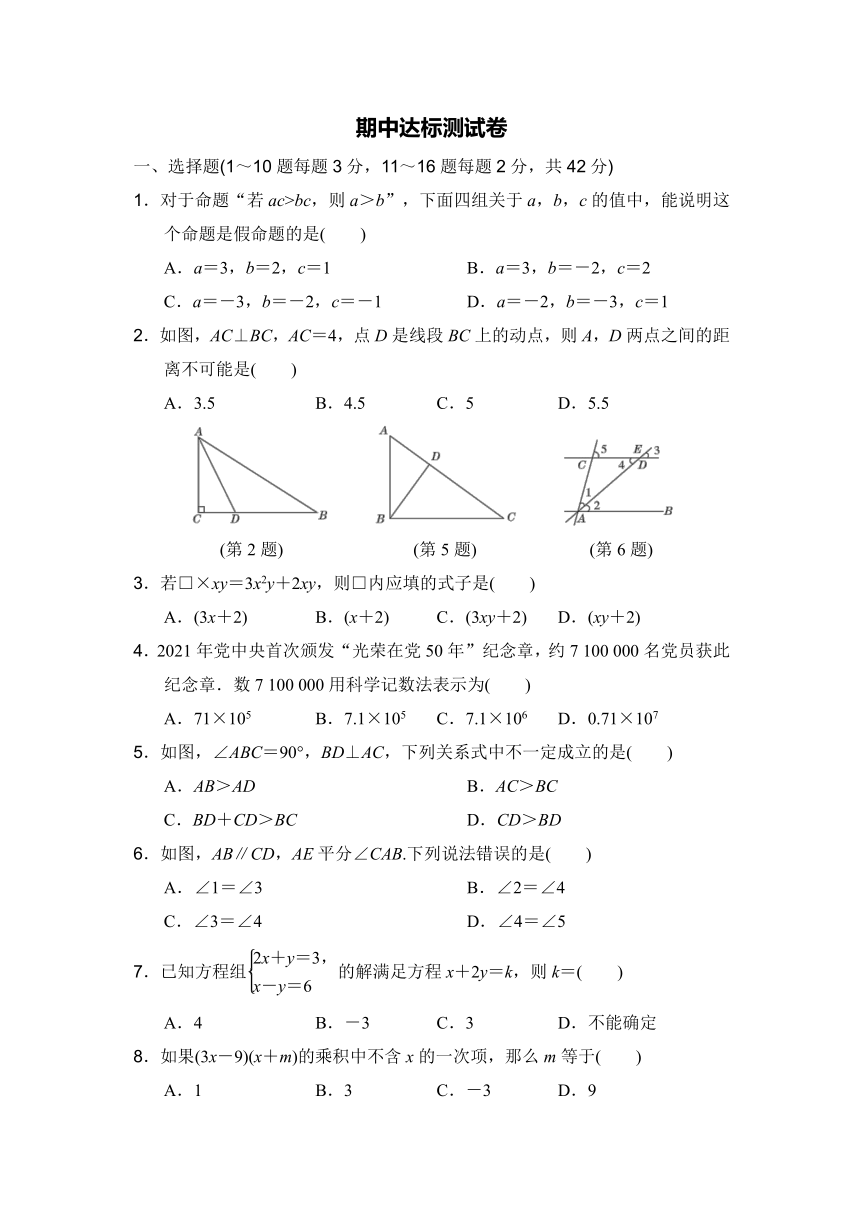 | |
| 格式 | doc | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 10:13:47 | ||
图片预览




文档简介
期中达标测试卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.对于命题“若ac>bc,则a>b”,下面四组关于a,b,c的值中,能说明这个命题是假命题的是( )
A.a=3,b=2,c=1 B.a=3,b=-2,c=2
C.a=-3,b=-2,c=-1 D.a=-2,b=-3,c=1
2.如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A,D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
(第2题) (第5题) (第6题)
3.若□×xy=3x2y+2xy,则□内应填的式子是( )
A.(3x+2) B.(x+2) C.(3xy+2) D.(xy+2)
4.2021年党中央首次颁发“光荣在党50年”纪念章,约7 100 000名党员获此纪念章.数7 100 000用科学记数法表示为( )
A.71×105 B.7.1×105 C.7.1×106 D.0.71×107
5.如图,∠ABC=90°,BD⊥AC,下列关系式中不一定成立的是( )
A.AB>AD B.AC>BC
C.BD+CD>BC D.CD>BD
6.如图,AB∥CD,AE平分∠CAB.下列说法错误的是( )
A.∠1=∠3 B.∠2=∠4
C.∠3=∠4 D.∠4=∠5
7.已知方程组的解满足方程x+2y=k,则k=( )
A.4 B.-3 C.3 D.不能确定
8.如果(3x-9)(x+m)的乘积中不含x的一次项,那么m等于( )
A.1 B.3 C.-3 D.9
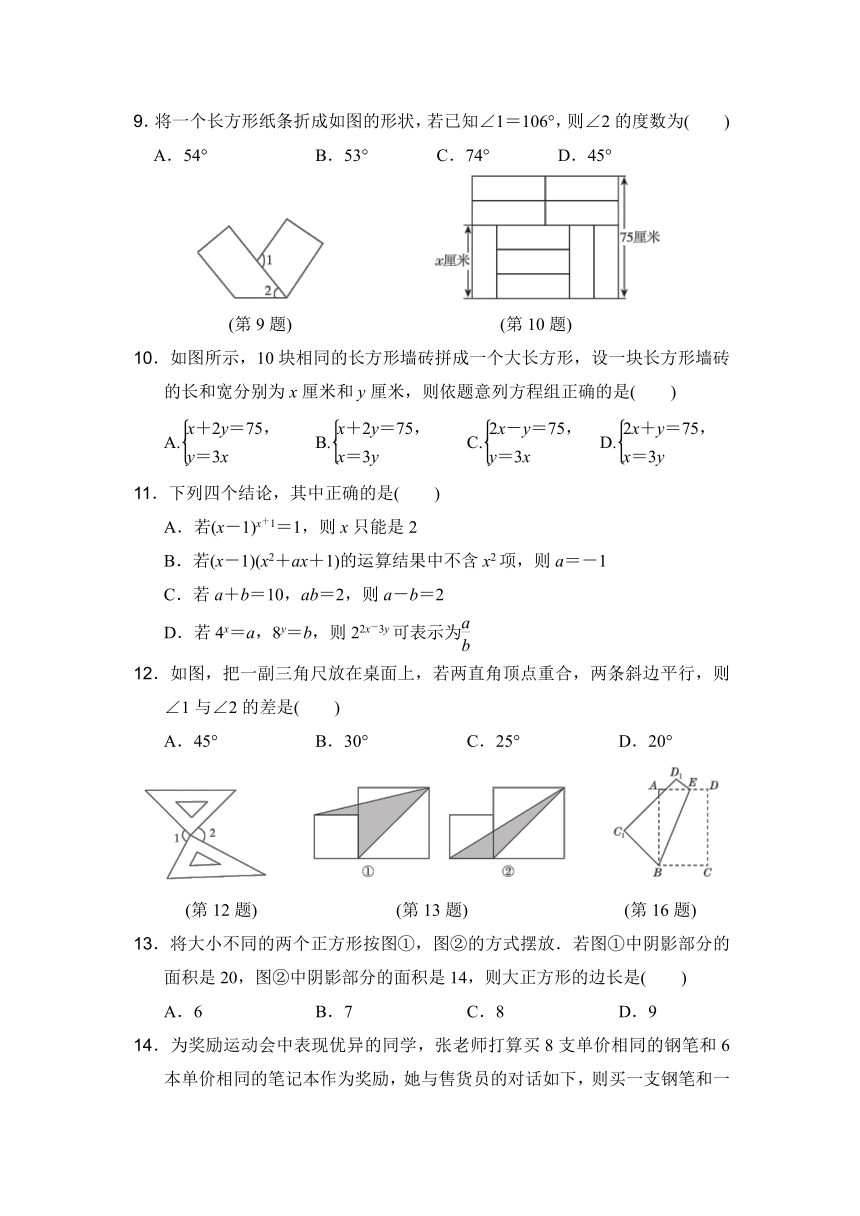
9.将一个长方形纸条折成如图的形状,若已知∠1=106°,则∠2的度数为( )
A.54° B.53° C.74° D.45°
(第9题) (第10题)
10.如图所示,10块相同的长方形墙砖拼成一个大长方形,设一块长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )
A. B. C. D.
11.下列四个结论,其中正确的是( )
A.若(x-1)x+1=1,则x只能是2
B.若(x-1)(x2+ax+1)的运算结果中不含x2项,则a=-1
C.若a+b=10,ab=2,则a-b=2
D.若4x=a,8y=b,则22x-3y可表示为
12.如图,把一副三角尺放在桌面上,若两直角顶点重合,两条斜边平行,则∠1与∠2的差是( )
A.45° B.30° C.25° D.20°
(第12题) (第13题) (第16题)
13.将大小不同的两个正方形按图①,图②的方式摆放.若图①中阴影部分的面积是20,图②中阴影部分的面积是14,则大正方形的边长是( )
A.6 B.7 C.8 D.9
14.为奖励运动会中表现优异的同学,张老师打算买8支单价相同的钢笔和6本单价相同的笔记本作为奖励,她与售货员的对话如下,则买一支钢笔和一本笔记本应付( )
老师:您好,我要买8支钢笔和6本笔记本.售货员:好的,那您应付款190元.老师:刚才我把两种文具的单价弄反了,以为要付160元.
A.22元 B.25元 C.27元 D.30元
15.已知a2+a-4=0,那么代数式a2(a+5)的值是( )
A.4 B.8 C.12 D.16
16.如图,长方形纸片ABCD沿着BE折叠,使C,D两点分别落在C1,D1处,若∠ABC1=45°,则∠ABE的度数为( )
A.21° B.21.5° C.22° D.22.5°
二、填空题(17,18题每题3分,19题每空3分,共12分)
17.《孙子算经》记载:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每3人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x辆车,有y人,则可列方程组为________.
(第19题)
18.已知(am)n=a6,(am)2÷an=a3,则4m2+n2=________.
19.在长方形ABCD中,放入6个形状、大小相同的小长方形,所标尺寸如图所示,则小长方形的长为______,阴影部分的面积为______.
三、解答题(20题8分,21~24题每题9分,25题10分,26题12分,共66分)
20.(1)解方程组
(2)先化简,再求值:(2x+1)2-(x+2y)(x-2y)-(2y)2,其中x=-1.
21.如图,EF∥AD,∠1=∠2.试说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
(第21题)
解:∵EF∥AD(已知),
∴∠2=________(____________).
又∵∠1=∠2(____________),
∴∠1=∠3(____________),
∴AB∥________(____________),
∴∠DGA+∠BAC=180°(____________).
22.如图所示,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,三角形ABC的三个顶点均在格点上.将三角形ABC先向右平移6个单位长度,再向上平移3个单位长度,得到三角形A1B1C1,画出平移后的三角形A1B1C1.
(第22题)
23.已知等式y=ax2+bx+c,当x=-1时,y=0;当x=1时,y=-4,当x=2时,y=3,求当x=5时,y的值.
24.甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“-a”,得到的结果为6x2-5x-6;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2+7x+6.
(1)求正确的a,b的值;
(2)计算这道乘法题的正确结果.
25.一批货物要运往某地,货主准备租用汽运公司的甲、乙两种货车,已知过去租用这两种货车运货的情况如下表所示.
甲货车辆数 乙货车辆数 累计运货吨数
第一次 3 4 54
第二次 2 3 39
(1)一辆甲货车和一辆乙货车一次分别运货多少吨?
(2)若货主现有45吨货物,计划同时租用甲货车a辆,乙货车b辆,一次运完,且恰好每辆车都装满货物.
①请你帮助货主设计租车方案;
②若甲货车每辆租金200元,乙货车每辆租金240元.请选出省钱的租车方案.
26.将一副三角尺中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)如图,当∠BCE=30°时,试说明CD∥AB的理由.
(2)若按住三角尺ABC不动,绕顶点C转动三角尺DCE,在旋转过程中始终要求点E在直线BC上方,当两块三角尺有一组边互相平行时,求∠BCE的度数.
(第26题)
答案
一、1.C 2.A 3.A 4.C 5.D 6.D 7.B 8.B 9.B 10.B
11.D 12.B 13.B 14.B
15.D 点拨:因为a2+a-4=0,
所以a2=-a+4,a2+a=4,
所以a2(a+5)=(-a+4)(a+5)=-a2-a+20=-(a2+a)+20=-4+20=16.故选D.
16.D 点拨:设∠ABE=x,
根据折叠前后角相等可知,
∠C1BE=∠CBE=45°+x,
因为∠ABC=90°,
所以45°+x+x=90°,
解得x=22.5°.故选D.
二、17.
18.33
19.8 cm;44 cm2 点拨:设小长方形的长为x cm,宽为y cm,
由题意得
解得
故阴影部分的面积为(6+2×2)×14-2×8×6=44(cm2).
三、20.解:(1)
①×3+②,得23x=46,解得x=2,
把x=2代入①,得12+3y=-3,解得y=-5,
所以原方程组的解是
(2)(2x+1)2-(x+2y)(x-2y)-(2y)2
=4x2+4x+1-x2+4y2-4y2
=3x2+4x+1,
当x=-1时,原式=3×(-1)2+4×(-1)+1=0.
21.∠3;两直线平行,同位角相等;已知;等量代换;DG;内错角相等,两直线平行;两直线平行,同旁内角互补
22.解:如图所示,三角形A1B1C1即为平移后的三角形.
(第22题)
23.解:根据题意得
①-②,得-2b=4,解得b=-2,
把b=-2代入①,得a+2+c=0,
即a+c=-2,④
把b=-2代入③,得4a-4+c=3,即4a+c=7,⑤
由④和⑤组成方程组
解得
所以y=3x2-2x-5.当x=5时,y=3×52-2×5-5=60.
24.解:(1)因为(2x-a)(3x+b)
=6x2+2bx-3ax-ab
=6x2+(2b-3a)x-ab,
所以2b-3a=-5.①
因为(2x+a)(x+b)=2x2+2bx+ax+ab=2x2+(2b+a)x+ab,
所以2b+a=7.②
由①和②组成方程组:
解得
(2)由(1)可知a=3,b=2,所以(2x+a)(3x+b)=(2x+3)·(3x+2)=6x2+13x+6.
25.解:(1)设一辆甲货车一次运货x吨,一辆乙货车一次运货y吨,
根据题意,得
解得
答:一辆甲货车一次运货6吨,一辆乙货车一次运货9吨.
(2)①由题可得:6a+9b=45,即b=5-a.
∵a,b均为正整数,
∴或
∴有2种运货方案.
方案一:租用甲货车3辆,乙货车3辆.
方案二:租用甲货车6辆,乙货车1辆.
②方案一所需费用为200×3+240×3=1 320(元).
方案二所需费用为200×6+240×1=1 440(元).
∵1 320<1 440,∴选方案一:租用甲货车3辆,乙货车3辆省钱.
26.解:(1)∵∠ACB=∠ECD=90°,
∴∠ACE+∠BCE=∠ACE+∠ACD=90°,
∴∠ACD=∠BCE=30°,
∵∠A=30°,∴∠A=∠ACD.
∴CD∥AB.
(2)①当AB∥CD时,由(1)知∠BCE=30°.
②如图①,当BC∥DE时,
∴∠BCE=∠E=45°.
③如图②,当AB∥CE时,
∴∠ACE=∠A=30°,
∴∠BCE=∠ACE+∠ACB=120°.
④如图③,当DE∥AC时,
∴∠ACE=∠E=45°,
∴∠BCE=∠ACE+∠ACB=135°.
⑤如图④,当AB∥DE时,延长BC交DE于F,
∵AB∥DE,∴∠CFD=∠B=60°,∴∠CFE=120°.
∵∠E=45°,
∴∠ECF=180°-120°-45°=15°,
∴∠BCE=180°-15°=165°.
综上:∠BCE的度数为30°或45°或120°或135°或165°.
(第26题)
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.对于命题“若ac>bc,则a>b”,下面四组关于a,b,c的值中,能说明这个命题是假命题的是( )
A.a=3,b=2,c=1 B.a=3,b=-2,c=2
C.a=-3,b=-2,c=-1 D.a=-2,b=-3,c=1
2.如图,AC⊥BC,AC=4,点D是线段BC上的动点,则A,D两点之间的距离不可能是( )
A.3.5 B.4.5 C.5 D.5.5
(第2题) (第5题) (第6题)
3.若□×xy=3x2y+2xy,则□内应填的式子是( )
A.(3x+2) B.(x+2) C.(3xy+2) D.(xy+2)
4.2021年党中央首次颁发“光荣在党50年”纪念章,约7 100 000名党员获此纪念章.数7 100 000用科学记数法表示为( )
A.71×105 B.7.1×105 C.7.1×106 D.0.71×107
5.如图,∠ABC=90°,BD⊥AC,下列关系式中不一定成立的是( )
A.AB>AD B.AC>BC
C.BD+CD>BC D.CD>BD
6.如图,AB∥CD,AE平分∠CAB.下列说法错误的是( )
A.∠1=∠3 B.∠2=∠4
C.∠3=∠4 D.∠4=∠5
7.已知方程组的解满足方程x+2y=k,则k=( )
A.4 B.-3 C.3 D.不能确定
8.如果(3x-9)(x+m)的乘积中不含x的一次项,那么m等于( )
A.1 B.3 C.-3 D.9
9.将一个长方形纸条折成如图的形状,若已知∠1=106°,则∠2的度数为( )
A.54° B.53° C.74° D.45°
(第9题) (第10题)
10.如图所示,10块相同的长方形墙砖拼成一个大长方形,设一块长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程组正确的是( )
A. B. C. D.
11.下列四个结论,其中正确的是( )
A.若(x-1)x+1=1,则x只能是2
B.若(x-1)(x2+ax+1)的运算结果中不含x2项,则a=-1
C.若a+b=10,ab=2,则a-b=2
D.若4x=a,8y=b,则22x-3y可表示为
12.如图,把一副三角尺放在桌面上,若两直角顶点重合,两条斜边平行,则∠1与∠2的差是( )
A.45° B.30° C.25° D.20°
(第12题) (第13题) (第16题)
13.将大小不同的两个正方形按图①,图②的方式摆放.若图①中阴影部分的面积是20,图②中阴影部分的面积是14,则大正方形的边长是( )
A.6 B.7 C.8 D.9
14.为奖励运动会中表现优异的同学,张老师打算买8支单价相同的钢笔和6本单价相同的笔记本作为奖励,她与售货员的对话如下,则买一支钢笔和一本笔记本应付( )
老师:您好,我要买8支钢笔和6本笔记本.售货员:好的,那您应付款190元.老师:刚才我把两种文具的单价弄反了,以为要付160元.
A.22元 B.25元 C.27元 D.30元
15.已知a2+a-4=0,那么代数式a2(a+5)的值是( )
A.4 B.8 C.12 D.16
16.如图,长方形纸片ABCD沿着BE折叠,使C,D两点分别落在C1,D1处,若∠ABC1=45°,则∠ABE的度数为( )
A.21° B.21.5° C.22° D.22.5°
二、填空题(17,18题每题3分,19题每空3分,共12分)
17.《孙子算经》记载:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文:今有若干人乘车,若每3人共乘一辆车,最终剩余2辆车;若每2人共乘一辆车,最终剩余9人无车可乘.问共有多少人?多少辆车?若设有x辆车,有y人,则可列方程组为________.
(第19题)
18.已知(am)n=a6,(am)2÷an=a3,则4m2+n2=________.
19.在长方形ABCD中,放入6个形状、大小相同的小长方形,所标尺寸如图所示,则小长方形的长为______,阴影部分的面积为______.
三、解答题(20题8分,21~24题每题9分,25题10分,26题12分,共66分)
20.(1)解方程组
(2)先化简,再求值:(2x+1)2-(x+2y)(x-2y)-(2y)2,其中x=-1.
21.如图,EF∥AD,∠1=∠2.试说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
(第21题)
解:∵EF∥AD(已知),
∴∠2=________(____________).
又∵∠1=∠2(____________),
∴∠1=∠3(____________),
∴AB∥________(____________),
∴∠DGA+∠BAC=180°(____________).
22.如图所示,在网格中,每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点,三角形ABC的三个顶点均在格点上.将三角形ABC先向右平移6个单位长度,再向上平移3个单位长度,得到三角形A1B1C1,画出平移后的三角形A1B1C1.
(第22题)
23.已知等式y=ax2+bx+c,当x=-1时,y=0;当x=1时,y=-4,当x=2时,y=3,求当x=5时,y的值.
24.甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“-a”,得到的结果为6x2-5x-6;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2+7x+6.
(1)求正确的a,b的值;
(2)计算这道乘法题的正确结果.
25.一批货物要运往某地,货主准备租用汽运公司的甲、乙两种货车,已知过去租用这两种货车运货的情况如下表所示.
甲货车辆数 乙货车辆数 累计运货吨数
第一次 3 4 54
第二次 2 3 39
(1)一辆甲货车和一辆乙货车一次分别运货多少吨?
(2)若货主现有45吨货物,计划同时租用甲货车a辆,乙货车b辆,一次运完,且恰好每辆车都装满货物.
①请你帮助货主设计租车方案;
②若甲货车每辆租金200元,乙货车每辆租金240元.请选出省钱的租车方案.
26.将一副三角尺中的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)如图,当∠BCE=30°时,试说明CD∥AB的理由.
(2)若按住三角尺ABC不动,绕顶点C转动三角尺DCE,在旋转过程中始终要求点E在直线BC上方,当两块三角尺有一组边互相平行时,求∠BCE的度数.
(第26题)
答案
一、1.C 2.A 3.A 4.C 5.D 6.D 7.B 8.B 9.B 10.B
11.D 12.B 13.B 14.B
15.D 点拨:因为a2+a-4=0,
所以a2=-a+4,a2+a=4,
所以a2(a+5)=(-a+4)(a+5)=-a2-a+20=-(a2+a)+20=-4+20=16.故选D.
16.D 点拨:设∠ABE=x,
根据折叠前后角相等可知,
∠C1BE=∠CBE=45°+x,
因为∠ABC=90°,
所以45°+x+x=90°,
解得x=22.5°.故选D.
二、17.
18.33
19.8 cm;44 cm2 点拨:设小长方形的长为x cm,宽为y cm,
由题意得
解得
故阴影部分的面积为(6+2×2)×14-2×8×6=44(cm2).
三、20.解:(1)
①×3+②,得23x=46,解得x=2,
把x=2代入①,得12+3y=-3,解得y=-5,
所以原方程组的解是
(2)(2x+1)2-(x+2y)(x-2y)-(2y)2
=4x2+4x+1-x2+4y2-4y2
=3x2+4x+1,
当x=-1时,原式=3×(-1)2+4×(-1)+1=0.
21.∠3;两直线平行,同位角相等;已知;等量代换;DG;内错角相等,两直线平行;两直线平行,同旁内角互补
22.解:如图所示,三角形A1B1C1即为平移后的三角形.
(第22题)
23.解:根据题意得
①-②,得-2b=4,解得b=-2,
把b=-2代入①,得a+2+c=0,
即a+c=-2,④
把b=-2代入③,得4a-4+c=3,即4a+c=7,⑤
由④和⑤组成方程组
解得
所以y=3x2-2x-5.当x=5时,y=3×52-2×5-5=60.
24.解:(1)因为(2x-a)(3x+b)
=6x2+2bx-3ax-ab
=6x2+(2b-3a)x-ab,
所以2b-3a=-5.①
因为(2x+a)(x+b)=2x2+2bx+ax+ab=2x2+(2b+a)x+ab,
所以2b+a=7.②
由①和②组成方程组:
解得
(2)由(1)可知a=3,b=2,所以(2x+a)(3x+b)=(2x+3)·(3x+2)=6x2+13x+6.
25.解:(1)设一辆甲货车一次运货x吨,一辆乙货车一次运货y吨,
根据题意,得
解得
答:一辆甲货车一次运货6吨,一辆乙货车一次运货9吨.
(2)①由题可得:6a+9b=45,即b=5-a.
∵a,b均为正整数,
∴或
∴有2种运货方案.
方案一:租用甲货车3辆,乙货车3辆.
方案二:租用甲货车6辆,乙货车1辆.
②方案一所需费用为200×3+240×3=1 320(元).
方案二所需费用为200×6+240×1=1 440(元).
∵1 320<1 440,∴选方案一:租用甲货车3辆,乙货车3辆省钱.
26.解:(1)∵∠ACB=∠ECD=90°,
∴∠ACE+∠BCE=∠ACE+∠ACD=90°,
∴∠ACD=∠BCE=30°,
∵∠A=30°,∴∠A=∠ACD.
∴CD∥AB.
(2)①当AB∥CD时,由(1)知∠BCE=30°.
②如图①,当BC∥DE时,
∴∠BCE=∠E=45°.
③如图②,当AB∥CE时,
∴∠ACE=∠A=30°,
∴∠BCE=∠ACE+∠ACB=120°.
④如图③,当DE∥AC时,
∴∠ACE=∠E=45°,
∴∠BCE=∠ACE+∠ACB=135°.
⑤如图④,当AB∥DE时,延长BC交DE于F,
∵AB∥DE,∴∠CFD=∠B=60°,∴∠CFE=120°.
∵∠E=45°,
∴∠ECF=180°-120°-45°=15°,
∴∠BCE=180°-15°=165°.
综上:∠BCE的度数为30°或45°或120°或135°或165°.
(第26题)
同课章节目录
