4.1.2 数列的递推公式课件(2)-2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册(共22张)
文档属性
| 名称 | 4.1.2 数列的递推公式课件(2)-2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 839.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 16:40:28 | ||
图片预览








文档简介
(共22张PPT)
4.1.2 数列的递推公式
选择性必修第二册 第四章 数列
例4 图中的三角形图案称为谢宾斯基(Sierpinski)三角形.在下图四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式。
(1)
(2)
(3)
(4)
这四个三角形图案中着色的小三角形的个数依次为1,3,9,27.
一、递推公式定义:
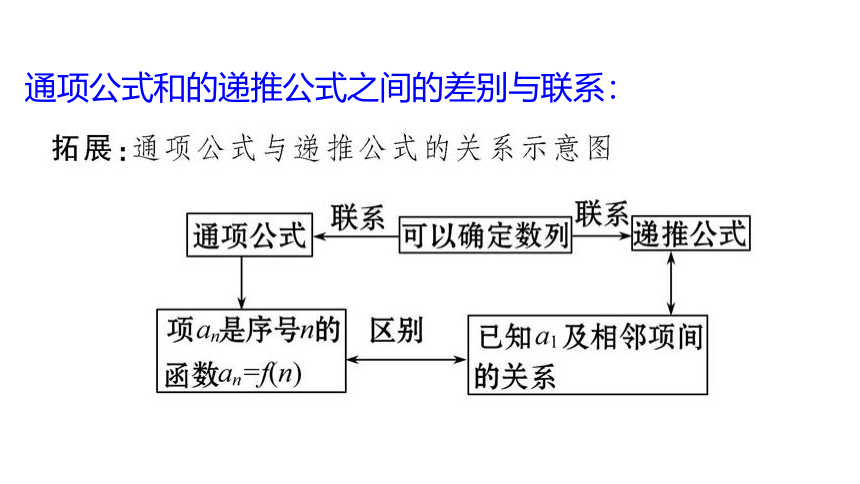
通项公式和的递推公式之间的差别与联系:
例1:已知下列数列的递推公式,写出此数列的前 4 项,
并推测数列的通项公式.
(1)数列{an}满足 an+1=2an+1,n∈N*,且 a1=-1;
(2)在数列{an}中,a1=1,an=an-1+
1
n(n-1)
(n≥2).
题型一 已知数列的递推公式,求前几项并猜出通项公式
练习1 根据递推公式,分别写出它的前 5 项,并归纳出通项公式:
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=
2an
an+2
(n∈N*).
解:(1)a1=0,a2=a1+1=1,a3=a2+3=4,
a4=a3+5=9,a5=a4+7=16.
由a1=02,a2=12,a3=22,a4=32,a5=42,
可归纳出an=(n-1)2.
例2:已知在数列{an}中,a1=5,an=an-1+3(n≥2),求数
列{an}的通项公式.
题型二 已知数列的递推公式,用累加法求通项公式
an=3n+2.
总结归纳:若数列有形如an+1=an+f(n)的递推公式,且可
求 f(1)+f(2)+…+f(n),可用累加法求通项公式.
例3:已知a1=2,an+1=2an,求an.
题型三 已知数列的递推公式,用累乘法求通项公式
思考
课堂小结
1.递推公式:(1)初始值;2)递推关系式
(1)已知数列的递推公式,求前几项并猜出通项公式
(2) 已知数列的递推公式,用累加法求通项公式
(3) 已知数列的递推公式,用累乘法求通项公式
训练提升:
课后作业
教材P8 练习
4.1.2 数列的递推公式
选择性必修第二册 第四章 数列
例4 图中的三角形图案称为谢宾斯基(Sierpinski)三角形.在下图四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式。
(1)
(2)
(3)
(4)
这四个三角形图案中着色的小三角形的个数依次为1,3,9,27.
一、递推公式定义:
通项公式和的递推公式之间的差别与联系:
例1:已知下列数列的递推公式,写出此数列的前 4 项,
并推测数列的通项公式.
(1)数列{an}满足 an+1=2an+1,n∈N*,且 a1=-1;
(2)在数列{an}中,a1=1,an=an-1+
1
n(n-1)
(n≥2).
题型一 已知数列的递推公式,求前几项并猜出通项公式
练习1 根据递推公式,分别写出它的前 5 项,并归纳出通项公式:
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=
2an
an+2
(n∈N*).
解:(1)a1=0,a2=a1+1=1,a3=a2+3=4,
a4=a3+5=9,a5=a4+7=16.
由a1=02,a2=12,a3=22,a4=32,a5=42,
可归纳出an=(n-1)2.
例2:已知在数列{an}中,a1=5,an=an-1+3(n≥2),求数
列{an}的通项公式.
题型二 已知数列的递推公式,用累加法求通项公式
an=3n+2.
总结归纳:若数列有形如an+1=an+f(n)的递推公式,且可
求 f(1)+f(2)+…+f(n),可用累加法求通项公式.
例3:已知a1=2,an+1=2an,求an.
题型三 已知数列的递推公式,用累乘法求通项公式
思考
课堂小结
1.递推公式:(1)初始值;2)递推关系式
(1)已知数列的递推公式,求前几项并猜出通项公式
(2) 已知数列的递推公式,用累加法求通项公式
(3) 已知数列的递推公式,用累乘法求通项公式
训练提升:
课后作业
教材P8 练习
