华师大版八年级上册15.2图形的旋转
图片预览








文档简介
(共24张PPT)
平移的定义:
在平面内,将一个图形沿某个方向移动
平移的性质:
经过平移,对应点所连的线段相等
平移不改变图形的形状和大小.
平移的特征:
一定的距离,这样的图形运动称为平移.
且平行(或在一直线上);对应线段相
等且平行(或在一直线上), 对应角相等.
1、平移改变的是图形的( )
A 位置 B 大小 C 形状 D 位置、大小和形状
2、经过平移,对应点所连的线段 ( )
A 平行 B 相等 C 平行且相等 D 以上都不对3、经过平移,图形上每个点都沿同一个方向移动了一段距离下面说法正确的是 ( )
A 不同的点移动的距离不同
B 不同的点移动的距离相同
C 不同的点移动的距离既可能相同也可能不同
D 不能确定
A
D
B
初二数学
花园二中数学组
动动脑筋:以上这些旋转运动有什么共同的特征?
这种转动现象,有什么共同的特征?
形状和大小改变吗?
实验步骤:
1、将透明胶片覆盖在△ABC上;
2、在薄透明胶片上画出与△ABC 重合的一个三角形;
3、用一枚图钉(O)固定,将透明胶片绕着图钉(O)转动,透明胶片上的三角形就旋转到了新的位置.
4、用透明胶固定,并给新的三角形标上字母。
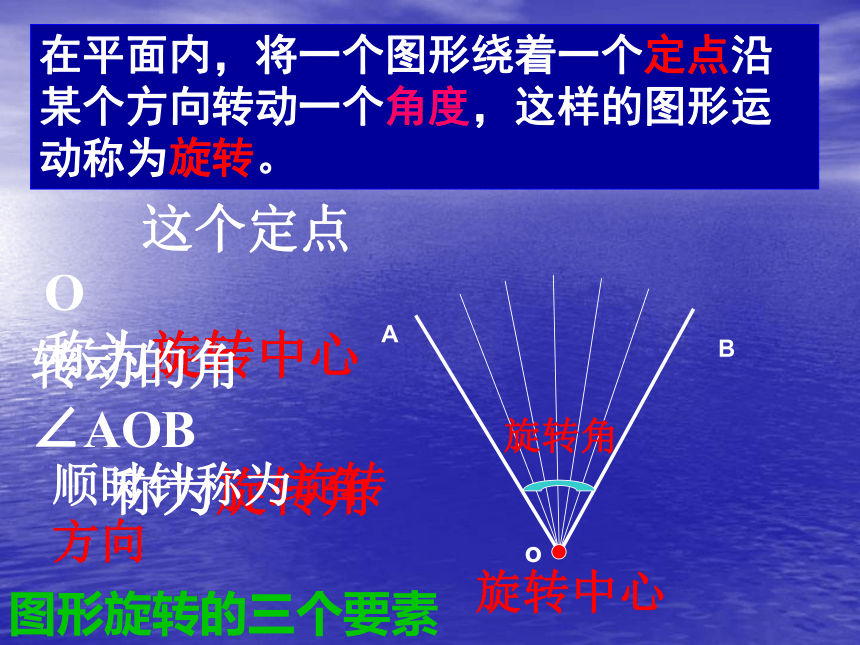
这个定点O
称为旋转中心
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
转动的角∠AOB
称为旋转角
图形旋转的三个要素
顺时针称为旋转方向
在平面内,将一个图形沿着某个方向移动
一定的距离,这样的图形运动称为平移.
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
平移不改变图形的大小和形状。
旋转不改变图形的大小和形状。
O
A’
B’
A
B
讨论回答:
图中,可以看到点A旋转到点A′,OA旋转到OA′, ∠AOB旋转到∠A′OB′,
这些都是互相对应的点、线段与角。那么点B的对应点是 ,线段OB的对应线段是线段 ;线段AB的对应线段是线段 ;∠A的
对应角是 ; ∠B的对应角是 ;旋转中心是点 ;旋转的角度是 。
B′
OB′
A′B′
∠A′
∠B′
O
45°
45°
如图,如果把钟表的指针看做四边形AOBC,它绕
着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是什么
⑵经过旋转,点A、B分别移动到什么位置?
⑶旋转角是什么?
⑷AO与DO的长有什么关系?BO与EO呢?
⑸∠AOD与∠BOE有什么大小关系?
议一议
旋转中心是O
点D和点E
的位置
AO=DO
BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
动态演示
O
P′
P
钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
例题1.
如图: ABC是等边三角形,D是BC
上一点, ABD经过 旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是顶点A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
例题2.
旋转角∠BAC
·
A
E
D
C
B
A
D
E
B
C
2.如图,正方形ABCD和正方形CBEF有公共边CB,请设计方案,使正方形ABCD旋转后能与正方形CBEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点B
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CB的
中点O旋转180°.
A
B
C
D
如图等腰直角 ABC逆时针旋转到 ADE, 使AD⊥BC, 垂足为O, 试说明:。
⑴旋转中心是哪一点?旋转角度是多少
⑵DE与AC的位置关系有什么特征
解:⑴旋转中心是顶点A,
旋转角度是∠BAD=45°;
⑵ DE⊥AC.
例题2.
A
B
C
D
E
┌
O
因为∠CAE=45°, 且∠E=45°.
A
B
C
P
Q
R
O
探索
如图△ABC是等边三角形,
△ ACQ和△BCR都是可以
由△ABP旋转得到的,
⑴分别说明旋转中心和
旋转角度;
⑵△BCR可以由△ACQ旋转得到吗
⑴旋转的概念:
在平面内,将一个图形绕着
一个定点沿某个方向转动一个角度的运动
⑵旋转的要素:
旋转不改变图形大小和形状,
只改变图形的位置.
叫做图形的旋转,简称旋转.
旋转中心和旋转角.
⑶旋转的特征:
再 见
如图等腰直角 ABC逆时针旋转到
ADE, 使AD⊥BC, 垂足为O, 试说明:。
⑴旋转中心是哪一点?旋转角度是多少
⑵DE与AC的位置关系有什么特征
解:⑴旋转中心是顶点A,
旋转角度是∠BAD=45°;
⑵ DE⊥AC.
例题3.
A
B
C
D
E
┌
O
因为∠CAE=45°, 且∠E=45°.
画 ABC绕点O逆时针旋转90°.
例题2.
旋转的画法2:
0
A
B
C
·
A′
B′
C′
90°
画法:
⑴连结OA、OB、OC;
⑵分别画OA、OB、OC
绕点O逆时针旋转90°
的线段OA、OB、OC ;
′
′
′
⑶顺次连结AB、BC、CA .
′
′
′
′
′
′
旋转的画法3:
例题2.
O
·
把下列格点图形顺时针旋转90°
A
A′
B′
这样旋转几次可以
与原来的图形重合
旋转的画法1:
画△ABC绕顶点A顺时针旋转45°的
图形.
A
B
C
B′
C′
画法:
45°
⑴以A为顶点, AB为边顺
时针方向作∠BAB =45°,
′
并截取AB =AB;
′
⑵同样画边AC , 并连结BC ;
′
′
′
则△ABC 就是所求作的旋转图形.
′
′
45°
你能说说旋转中有哪些对应元素吗
例题2.
平移的定义:
在平面内,将一个图形沿某个方向移动
平移的性质:
经过平移,对应点所连的线段相等
平移不改变图形的形状和大小.
平移的特征:
一定的距离,这样的图形运动称为平移.
且平行(或在一直线上);对应线段相
等且平行(或在一直线上), 对应角相等.
1、平移改变的是图形的( )
A 位置 B 大小 C 形状 D 位置、大小和形状
2、经过平移,对应点所连的线段 ( )
A 平行 B 相等 C 平行且相等 D 以上都不对3、经过平移,图形上每个点都沿同一个方向移动了一段距离下面说法正确的是 ( )
A 不同的点移动的距离不同
B 不同的点移动的距离相同
C 不同的点移动的距离既可能相同也可能不同
D 不能确定
A
D
B
初二数学
花园二中数学组
动动脑筋:以上这些旋转运动有什么共同的特征?
这种转动现象,有什么共同的特征?
形状和大小改变吗?
实验步骤:
1、将透明胶片覆盖在△ABC上;
2、在薄透明胶片上画出与△ABC 重合的一个三角形;
3、用一枚图钉(O)固定,将透明胶片绕着图钉(O)转动,透明胶片上的三角形就旋转到了新的位置.
4、用透明胶固定,并给新的三角形标上字母。
这个定点O
称为旋转中心
旋转角
旋转中心
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。
A
o
B
转动的角∠AOB
称为旋转角
图形旋转的三个要素
顺时针称为旋转方向
在平面内,将一个图形沿着某个方向移动
一定的距离,这样的图形运动称为平移.
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转
平移不改变图形的大小和形状。
旋转不改变图形的大小和形状。
O
A’
B’
A
B
讨论回答:
图中,可以看到点A旋转到点A′,OA旋转到OA′, ∠AOB旋转到∠A′OB′,
这些都是互相对应的点、线段与角。那么点B的对应点是 ,线段OB的对应线段是线段 ;线段AB的对应线段是线段 ;∠A的
对应角是 ; ∠B的对应角是 ;旋转中心是点 ;旋转的角度是 。
B′
OB′
A′B′
∠A′
∠B′
O
45°
45°
如图,如果把钟表的指针看做四边形AOBC,它绕
着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是什么
⑵经过旋转,点A、B分别移动到什么位置?
⑶旋转角是什么?
⑷AO与DO的长有什么关系?BO与EO呢?
⑸∠AOD与∠BOE有什么大小关系?
议一议
旋转中心是O
点D和点E
的位置
AO=DO
BO=EO
∠AOD=∠BOE
∠AOD和∠BOE都是旋转角
动态演示
O
P′
P
钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?
例题1.
如图: ABC是等边三角形,D是BC
上一点, ABD经过 旋转后到达 ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?
E
D
C
B
A
M
.
解:(1)旋转中心是顶点A;
(2)旋转了60度;
(3)点M转到了AC的中点位置上.
例题2.
旋转角∠BAC
·
A
E
D
C
B
A
D
E
B
C
2.如图,正方形ABCD和正方形CBEF有公共边CB,请设计方案,使正方形ABCD旋转后能与正方形CBEF重合,你能写出几种方案
A
B
C
D
E
F
·
O
解:
方案一:
把正方形ABCD绕点B
顺时针旋转90°.
方案二:
把正方形ABCD绕点C
逆时针旋转90°.
方案三:
把正方形ABCD绕CB的
中点O旋转180°.
A
B
C
D
如图等腰直角 ABC逆时针旋转到 ADE, 使AD⊥BC, 垂足为O, 试说明:。
⑴旋转中心是哪一点?旋转角度是多少
⑵DE与AC的位置关系有什么特征
解:⑴旋转中心是顶点A,
旋转角度是∠BAD=45°;
⑵ DE⊥AC.
例题2.
A
B
C
D
E
┌
O
因为∠CAE=45°, 且∠E=45°.
A
B
C
P
Q
R
O
探索
如图△ABC是等边三角形,
△ ACQ和△BCR都是可以
由△ABP旋转得到的,
⑴分别说明旋转中心和
旋转角度;
⑵△BCR可以由△ACQ旋转得到吗
⑴旋转的概念:
在平面内,将一个图形绕着
一个定点沿某个方向转动一个角度的运动
⑵旋转的要素:
旋转不改变图形大小和形状,
只改变图形的位置.
叫做图形的旋转,简称旋转.
旋转中心和旋转角.
⑶旋转的特征:
再 见
如图等腰直角 ABC逆时针旋转到
ADE, 使AD⊥BC, 垂足为O, 试说明:。
⑴旋转中心是哪一点?旋转角度是多少
⑵DE与AC的位置关系有什么特征
解:⑴旋转中心是顶点A,
旋转角度是∠BAD=45°;
⑵ DE⊥AC.
例题3.
A
B
C
D
E
┌
O
因为∠CAE=45°, 且∠E=45°.
画 ABC绕点O逆时针旋转90°.
例题2.
旋转的画法2:
0
A
B
C
·
A′
B′
C′
90°
画法:
⑴连结OA、OB、OC;
⑵分别画OA、OB、OC
绕点O逆时针旋转90°
的线段OA、OB、OC ;
′
′
′
⑶顺次连结AB、BC、CA .
′
′
′
′
′
′
旋转的画法3:
例题2.
O
·
把下列格点图形顺时针旋转90°
A
A′
B′
这样旋转几次可以
与原来的图形重合
旋转的画法1:
画△ABC绕顶点A顺时针旋转45°的
图形.
A
B
C
B′
C′
画法:
45°
⑴以A为顶点, AB为边顺
时针方向作∠BAB =45°,
′
并截取AB =AB;
′
⑵同样画边AC , 并连结BC ;
′
′
′
则△ABC 就是所求作的旋转图形.
′
′
45°
你能说说旋转中有哪些对应元素吗
例题2.
