2021-2022学年八年级数学教版上册14.2.3完全平方公式添括号法则课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年八年级数学教版上册14.2.3完全平方公式添括号法则课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 536.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 10:16:25 | ||
图片预览






文档简介
(共18张PPT)
14.2.3 完全平方公式添括号法则
回顾与思考
(2)(-2a+b)2
(3)(-2+y)2
(1) (3x+2)(-2+3x)
(4) (a + b +c ) 2
计算
如何计算
思考:如何计算 (a + b +c ) 2
可以用乘法公式来计算吗?
解原式=(a + b +c )(a + b +c )
= a 2 +ab+ac+ba+b2+bc+ac+bc+c2
= a 2 +b2+c2+2ab+2bc+2ac
解原式=[a +( b +c )]2
= a 2 +( b +c )2+2a( b +c )
= a 2 +b2+c2+2ab+2bc+2ac
乘方的意义
整体思想
乘方公式
如何添括号来实现更简便的计算?
去括号的法则是什么?
括号前面是“+”号,去括号后把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,去括号后把括号和它前 面的“-”号去掉,括号里各项都改变正负号。
1.去括号:
解:
(4)a-(b-c)=a-b+c
(1)a+(b-c)=a+b-c
(2)a+(-b-c)=a-b-c
(3)a-(-b+c)=a+b-c
a+b-c=a+(b-c)
a-b-c=a+(-b-c)
a+b-c=a-(-b+c)
a-b+c=a-(b-c)
去括号
反过来
添括号
3
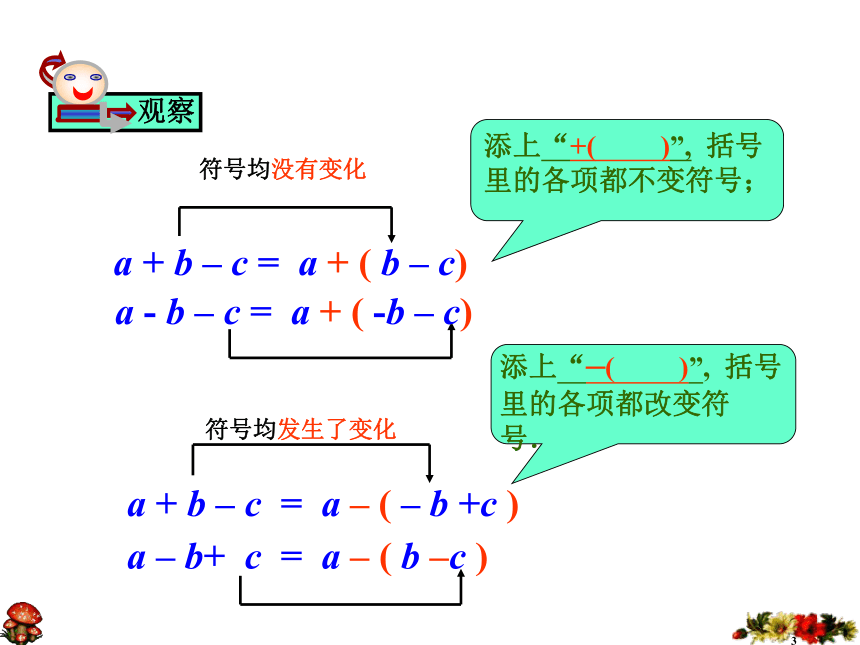
a + b – c = a + ( b – c)
符号均没有变化
a + b – c = a – ( – b +c )
符号均发生了变化
添上“+( )”, 括号里的各项都不变符号;
添上“–( )”, 括号里的各项都改变符号.
观察
a - b – c = a + ( -b – c)
a – b+ c = a – ( b –c )
去括号的法则
括号前面是“+”号,去括号后把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,去括号后把括号和它前面的“-”号去掉,括号里各项都改变正负号。
添括号的法则
添括号后如果括号前面是正号,括到括号里的各项都不变符号;
添括号后如果括号前面是负号,括到括号里的各项都改变符号.
+(正括号)不变,- (负括号)全变.
2.在括号内填入适当的项:
(1) x –x+1 = x –( );
(2) 2 x –3 x–1= 2 x +( );
(3)(a–b)–(c–d)= a –( ).
x–1
–3x–1
b + c – d
3、下列等号右边添的括号正确吗?
若不正确,可怎样改正?
用去括号法则来检验添括号是否正确
例1、运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.
解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9.
(a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.
(a + 2b – 1 ) 2 (2) (2x +y +z ) (2x – y – z )
= _____________ =___________________
变式.先将式子变形,后自选两道题再计算。
(3)(a-b+c)(a+b-c) (4)(2a+3b-1)(1-2a-3b)
= _____________ = _______________
只有符号不同的两个三项式相乘,通过添括号都可以将算式变形,运用平方差公式(一同两反)或完全平方公式(三项全反)计算。
[2x+(y+z)][2x-(y+z)]
[a-(b-c)][a+(b-c)]
(2a+3b-1)[-(2a+3b-1)]
[a+(2b-1)]2
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
常用
结论
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
当堂练习
1.判断下列运算是否正确.
(1)2a-b-c=2a -(b-c)
(2)m-3n+2a-b= m +(3n+2a-b)
(3)2x-3y+2= -(2x+3y-2)
(4)a-2b-4c+5=(a-2b)-(4c-5)
2.根据条件解答下列各题.
①已知 m-3n=5,求15-2m+6n的值
②已知 (2x-2y+3)(2x-2y-3)=7,求x-y的值
3.已知x+y=8,x-y=4,求xy的值.
4.已知x+=3, 求 的值.
4.观察并填空
① (a + ) = a2 + 6ab+ ( ) 2
② ( - ) = 4x2 – 12xy+ ( ) 2
如果(x+a) = x2 + kx+ 4 那么 a = 。
变式训练 如果9x2-mxy+16y 可化为一个
整式的平方,则 m=_____.
2
首平方加尾平方加首尾积2倍的二次三项式
5.阅读与思考
我国古代在数学方面的许多发现都曾位居世界前列,其中“杨辉三角”就是一例:如图
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
(a+b)= a+b
(a+b) = a +2ab+b
(a+b) = a +3a b+3ab +b
=
①写出展开式
……
尝试验证下面结论
三个代数式知二必求三
14.2.3 完全平方公式添括号法则
回顾与思考
(2)(-2a+b)2
(3)(-2+y)2
(1) (3x+2)(-2+3x)
(4) (a + b +c ) 2
计算
如何计算
思考:如何计算 (a + b +c ) 2
可以用乘法公式来计算吗?
解原式=(a + b +c )(a + b +c )
= a 2 +ab+ac+ba+b2+bc+ac+bc+c2
= a 2 +b2+c2+2ab+2bc+2ac
解原式=[a +( b +c )]2
= a 2 +( b +c )2+2a( b +c )
= a 2 +b2+c2+2ab+2bc+2ac
乘方的意义
整体思想
乘方公式
如何添括号来实现更简便的计算?
去括号的法则是什么?
括号前面是“+”号,去括号后把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,去括号后把括号和它前 面的“-”号去掉,括号里各项都改变正负号。
1.去括号:
解:
(4)a-(b-c)=a-b+c
(1)a+(b-c)=a+b-c
(2)a+(-b-c)=a-b-c
(3)a-(-b+c)=a+b-c
a+b-c=a+(b-c)
a-b-c=a+(-b-c)
a+b-c=a-(-b+c)
a-b+c=a-(b-c)
去括号
反过来
添括号
3
a + b – c = a + ( b – c)
符号均没有变化
a + b – c = a – ( – b +c )
符号均发生了变化
添上“+( )”, 括号里的各项都不变符号;
添上“–( )”, 括号里的各项都改变符号.
观察
a - b – c = a + ( -b – c)
a – b+ c = a – ( b –c )
去括号的法则
括号前面是“+”号,去括号后把括号和它前面的“+”号去掉,括号里各项都不改变正负号。
括号前面是“-”号,去括号后把括号和它前面的“-”号去掉,括号里各项都改变正负号。
添括号的法则
添括号后如果括号前面是正号,括到括号里的各项都不变符号;
添括号后如果括号前面是负号,括到括号里的各项都改变符号.
+(正括号)不变,- (负括号)全变.
2.在括号内填入适当的项:
(1) x –x+1 = x –( );
(2) 2 x –3 x–1= 2 x +( );
(3)(a–b)–(c–d)= a –( ).
x–1
–3x–1
b + c – d
3、下列等号右边添的括号正确吗?
若不正确,可怎样改正?
用去括号法则来检验添括号是否正确
例1、运用乘法公式计算:
(1) ( x +2y-3) (x- 2y +3) ; (2) (a + b +c ) 2.
解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9.
(a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac.
(a + 2b – 1 ) 2 (2) (2x +y +z ) (2x – y – z )
= _____________ =___________________
变式.先将式子变形,后自选两道题再计算。
(3)(a-b+c)(a+b-c) (4)(2a+3b-1)(1-2a-3b)
= _____________ = _______________
只有符号不同的两个三项式相乘,通过添括号都可以将算式变形,运用平方差公式(一同两反)或完全平方公式(三项全反)计算。
[2x+(y+z)][2x-(y+z)]
[a-(b-c)][a+(b-c)]
(2a+3b-1)[-(2a+3b-1)]
[a+(2b-1)]2
课堂小结
完全平方公式
法则
注意
(a±b)2= a2 ±2ab+b2
1.项数、符号、字母及其指数
2.不能直接应用公式进行计算的式子,可能需要先添括号变形成符合公式的要求才行
常用
结论
3.弄清完全平方公式和平方差公式不同(从公式结构特点及结果两方面)
a2+b2=(a+b)2-2ab=(a-b)2+2ab;
4ab=(a+b)2-(a-b)2.
当堂练习
1.判断下列运算是否正确.
(1)2a-b-c=2a -(b-c)
(2)m-3n+2a-b= m +(3n+2a-b)
(3)2x-3y+2= -(2x+3y-2)
(4)a-2b-4c+5=(a-2b)-(4c-5)
2.根据条件解答下列各题.
①已知 m-3n=5,求15-2m+6n的值
②已知 (2x-2y+3)(2x-2y-3)=7,求x-y的值
3.已知x+y=8,x-y=4,求xy的值.
4.已知x+=3, 求 的值.
4.观察并填空
① (a + ) = a2 + 6ab+ ( ) 2
② ( - ) = 4x2 – 12xy+ ( ) 2
如果(x+a) = x2 + kx+ 4 那么 a = 。
变式训练 如果9x2-mxy+16y 可化为一个
整式的平方,则 m=_____.
2
首平方加尾平方加首尾积2倍的二次三项式
5.阅读与思考
我国古代在数学方面的许多发现都曾位居世界前列,其中“杨辉三角”就是一例:如图
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
(a+b)= a+b
(a+b) = a +2ab+b
(a+b) = a +3a b+3ab +b
=
①写出展开式
……
尝试验证下面结论
三个代数式知二必求三
