新人教版七年级上册2.1.2多项式
文档属性
| 名称 | 新人教版七年级上册2.1.2多项式 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-10 09:11:10 | ||
图片预览





文档简介
(共12张PPT)
单项式的注意点
比如 -3,0,m, 等都是单项式。
1.单独一个数或一个字母也叫单项式!
3.单项式的系数包含符号,当系数为1或—1时,
这个“1”应省略不写。
2.单独一个非零数的次数是0。
比如-3的次数是0
00是没意义的
-3ab2的系数?
观察 & 探究
我们来看下列式子
, , , ,
这些式子有什么特点?
3x+5y+2z
ab- πr2
2
1
(x2+2x+18)
上面这些代数式的共同特点是:都是由几个单项式的和组成的。
多项式(polynomial):几个单项式的和。
例1。判断. 下列代数式哪些是多项式
单项式
单项式
x2+2x+18
v-2.5
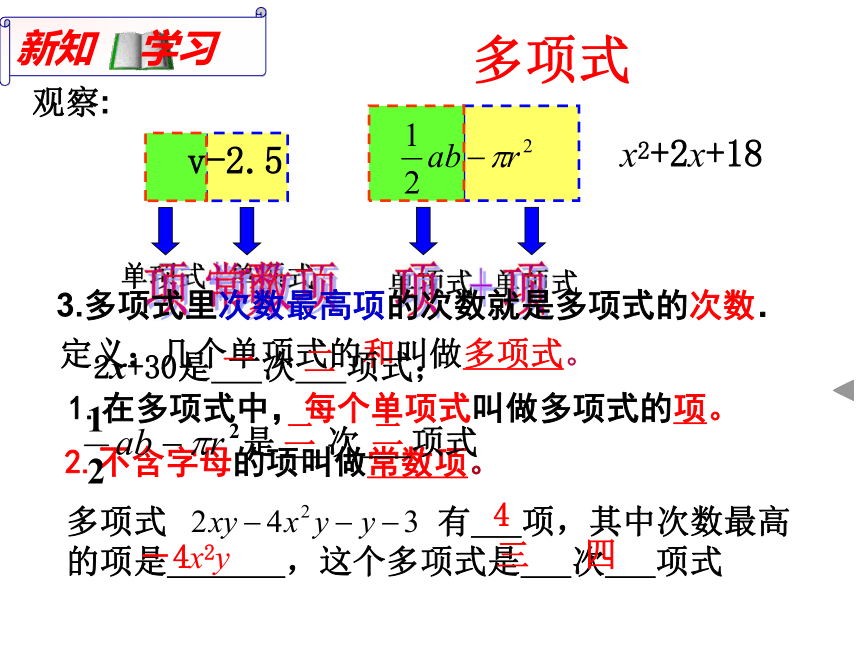
定义:几个单项式的和叫做多项式。
1.在多项式中,每个单项式叫做多项式的项。
2.不含字母的项叫做常数项。
新知 学习
单项式
单项式
多项式
观察:
3.多项式里次数最高项的次数就是多项式的次数.
2x+30是 次 项式;
是 次 项式
一
二
二
二
多项式 有 项,其中次数最高的项是 ,这个多项式是 次 项式
4
-4x2y
三
四
(1)多项式a3-a2b2+5ab2-3b有____项,分别是____,_____,______,
_____,其中次数最高的项是______,最高项的次数为____,这一项
的系数是__,其中一次项的系数是__.
巩固练习1:
(2)多项式x3-2x2y+3xy2+5看作是_____,______,______,____的和.
其中它的常数项是_____,次数最高的项是____,______,______,
它们的次数都是_____,
4
a3
-a2b2
5ab2
-3b
-a2b2
4
x3
-2x2y
3xy2
x3
-2x2y
3xy2
四次四项式
5
3
5
三次四项式
1次
3次
3次
4次
3次
3次
3次
-1
-3
单项式和多项式通称整式
反馈练习
2.判断正误:
1.x2–2xy+y2是六次三项式( )
2.a3 –5a2b2+4a2b –6b3的次数是3( )
3.多项式2x2 –3xy+y2的项有2x2 , 3xy , y2三项( )
×
×
×
注意:
1、多项式的次数不是所有项的次数之和。
2、寻找多项式次数的方法:
I 先计算出每一个单项式的次数,
II 再挑选哪一个单项式的次数高,次数最高项的次数就是多项式的次数。
3、多项式的每一项都包括它前面的符号。
例3 判断下列各代数式是否是整式。
(1)1 (2) –n (3)
(4) (5)2x+1 (6)
解: 单项式有: 1, –n , ,
多项式有 2x+1 , ,它们都是整式
它既不是单项式,也不是多项式,所以它不是整式。它是以后将学习的分式。
4、下列说法正确的是( )
A、 是多项式 B、3x4 – 5x2y2 –6y4 –2是四次四项式
C、x6 – 1的项数和次数都等于6 D、 是整式
B
成长的足迹
1. 单项式m2n2的系数是_______,
次数是______, m2n2是____次单项式.
2. 多项式x+y-z是单项式 , ,___的和,它是___次___项式.
3. 多项式3m3-2m-5+m2的常数项是____,
一次项是_____, 二次项的系数是_____.
1
4
四
x
y
-z
一
三
-5
-2m
1
4.一个关于字母x的二次三项式的二次项 系数为4,一次项系数为1,常数项为7
则这个二次三项式为_______.
4x2+x+7
5.若多项式x4-(a-1)x3+5x2-(b+3)x-1中不含x3和x项,
求a+ba的值
6.若多项式6xn+2-x2-n+2是关于x的三次三项式,
求整式n2-2n+1的值
7.有一个多项式为 , 按这样的规律写下去,写出它的第八项和最后一项。这个多项式是几次几项式?
8. 多项式- x y + xy -3x +6是六次四项式,
单项式3x y 的次数与这个多项式的次数相同。求
m+n的值
9.已知n是自然数,多项式 y n+1+3x3-2x是三次三项式,那么n可以是哪些数?
练习:判断下列说法是否正确.
(2)x+y是二次二项式;
(3)多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、
b3,次数为12
(4)多项式3n4-2n2+1的次数为4,常数项为1
(1)式子2x2+3x+3的一次项的系数是2.
( )
( )
( )
( )
运用新知1:
(5)多项式3n4-(m-2)n2+1,当m=2时,这个多项式
叫四次三项式。
( )
次数:所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
单项式的注意点
比如 -3,0,m, 等都是单项式。
1.单独一个数或一个字母也叫单项式!
3.单项式的系数包含符号,当系数为1或—1时,
这个“1”应省略不写。
2.单独一个非零数的次数是0。
比如-3的次数是0
00是没意义的
-3ab2的系数?
观察 & 探究
我们来看下列式子
, , , ,
这些式子有什么特点?
3x+5y+2z
ab- πr2
2
1
(x2+2x+18)
上面这些代数式的共同特点是:都是由几个单项式的和组成的。
多项式(polynomial):几个单项式的和。
例1。判断. 下列代数式哪些是多项式
单项式
单项式
x2+2x+18
v-2.5
定义:几个单项式的和叫做多项式。
1.在多项式中,每个单项式叫做多项式的项。
2.不含字母的项叫做常数项。
新知 学习
单项式
单项式
多项式
观察:
3.多项式里次数最高项的次数就是多项式的次数.
2x+30是 次 项式;
是 次 项式
一
二
二
二
多项式 有 项,其中次数最高的项是 ,这个多项式是 次 项式
4
-4x2y
三
四
(1)多项式a3-a2b2+5ab2-3b有____项,分别是____,_____,______,
_____,其中次数最高的项是______,最高项的次数为____,这一项
的系数是__,其中一次项的系数是__.
巩固练习1:
(2)多项式x3-2x2y+3xy2+5看作是_____,______,______,____的和.
其中它的常数项是_____,次数最高的项是____,______,______,
它们的次数都是_____,
4
a3
-a2b2
5ab2
-3b
-a2b2
4
x3
-2x2y
3xy2
x3
-2x2y
3xy2
四次四项式
5
3
5
三次四项式
1次
3次
3次
4次
3次
3次
3次
-1
-3
单项式和多项式通称整式
反馈练习
2.判断正误:
1.x2–2xy+y2是六次三项式( )
2.a3 –5a2b2+4a2b –6b3的次数是3( )
3.多项式2x2 –3xy+y2的项有2x2 , 3xy , y2三项( )
×
×
×
注意:
1、多项式的次数不是所有项的次数之和。
2、寻找多项式次数的方法:
I 先计算出每一个单项式的次数,
II 再挑选哪一个单项式的次数高,次数最高项的次数就是多项式的次数。
3、多项式的每一项都包括它前面的符号。
例3 判断下列各代数式是否是整式。
(1)1 (2) –n (3)
(4) (5)2x+1 (6)
解: 单项式有: 1, –n , ,
多项式有 2x+1 , ,它们都是整式
它既不是单项式,也不是多项式,所以它不是整式。它是以后将学习的分式。
4、下列说法正确的是( )
A、 是多项式 B、3x4 – 5x2y2 –6y4 –2是四次四项式
C、x6 – 1的项数和次数都等于6 D、 是整式
B
成长的足迹
1. 单项式m2n2的系数是_______,
次数是______, m2n2是____次单项式.
2. 多项式x+y-z是单项式 , ,___的和,它是___次___项式.
3. 多项式3m3-2m-5+m2的常数项是____,
一次项是_____, 二次项的系数是_____.
1
4
四
x
y
-z
一
三
-5
-2m
1
4.一个关于字母x的二次三项式的二次项 系数为4,一次项系数为1,常数项为7
则这个二次三项式为_______.
4x2+x+7
5.若多项式x4-(a-1)x3+5x2-(b+3)x-1中不含x3和x项,
求a+ba的值
6.若多项式6xn+2-x2-n+2是关于x的三次三项式,
求整式n2-2n+1的值
7.有一个多项式为 , 按这样的规律写下去,写出它的第八项和最后一项。这个多项式是几次几项式?
8. 多项式- x y + xy -3x +6是六次四项式,
单项式3x y 的次数与这个多项式的次数相同。求
m+n的值
9.已知n是自然数,多项式 y n+1+3x3-2x是三次三项式,那么n可以是哪些数?
练习:判断下列说法是否正确.
(2)x+y是二次二项式;
(3)多项式a3-a2b+ab2-b3的项为a3、a2b、ab2、
b3,次数为12
(4)多项式3n4-2n2+1的次数为4,常数项为1
(1)式子2x2+3x+3的一次项的系数是2.
( )
( )
( )
( )
运用新知1:
(5)多项式3n4-(m-2)n2+1,当m=2时,这个多项式
叫四次三项式。
( )
次数:所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
