华师大版七年级下册:第7章《一次方程组》达标测试卷(word版,含答案)
文档属性
| 名称 | 华师大版七年级下册:第7章《一次方程组》达标测试卷(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 447.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 08:02:22 | ||
图片预览



文档简介
第7章达标测试卷
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列方程中,是二元一次方程的是( )
A.8x2+1=y B.y=8x+1 C.y= D.xy=1
2.若是关于x,y的方程ax-y=3的解,则a的值是( )
A.1 B.2 C.3 D.4
3.表格中上下每对x,y的值都是同一个二元一次方程的解,则这个方程为( )
x -1 0 1 2
y 8 5 2 -1
A.5x+y=3 B.x+y=5
C.2x-y=0 D.3x+y=5
4.已知(x-y-3)2+|x+y-1|=0,则yx的值为( )
A.-1 B.1 C.-2 D.2
5.若方程组的解是二元一次方程3x-5y-90=0的一个解,则a的值是( )
A.3 B.2 C.6 D.7
6.关于x,y的方程组的解是其中y的值被盖住了,不过仍能求出p,则p的值是( )
A.- B. C.- D.
7.如图,在某张桌子上放相同的木块,图中R=38 cm,S=102 cm,则桌子的高度是( )
INCLUDEPICTURE"1.tif" INCLUDEPICTURE "D:\\方正转Word\\7HS福建\\1.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\福建\\7HS福建\\1.tif" \* MERGEFORMATINET
(第7题)
A.70 cm B.50 cm C.65 cm D.14 cm
8.把一根9 m长的钢管截成1 m长和2 m长两种规格均有的短钢管,且没有余料,设某截法中1 m长的钢管有a根,则a的值可能有( )
A.3种 B.4种 C.5种 D.9种
9.我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上.乙说得甲九只,两家之数相当.二人闲坐恼心肠,画地算了半晌.”翻译成现代文,其大意如下:甲乙两人隔一条沟放牧,二人心里暗中合计.甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.请问甲乙各有多少只羊呢?设甲有羊x只,乙有羊y只,则符合题意的方程组是( )
A. B.
C. D.
10.小明说为方程ax+by=10的解,小慧说为方程ax+by=10的解,两人谁也不能说服对方,如果你想让他们的解都正确,则需要添加的条件是( )
A.a=12,b=10 B.a=9,b=10
C.a=10,b=11 D.a=10,b=10
二、填空题(本题共6小题,每小题3分,共18分)
11.已知方程5x-y=7,用含x的代数式表示y,y=________.
12.写一个以为解的二元一次方程组:________.
13.已知(a-2)x|a|-1+3y=1是关于x,y的二元一次方程,则a=________.
14.定义一种新运算“※”,规定:a※b=+.已知1※2=8,(-2)※3=4,则3※(-4)等于________.
15.甲袋中装有黄金9枚(每枚黄金质量相同),乙袋中装有白银11枚(每枚白银质量相同),两袋质量相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子的质量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意可列方程组为______________.
16.甲、乙、丙三种商品,若购买甲商品3件、乙商品2件、丙商品1件,共需215元,购买甲商品1件、乙商品2件、丙商品3件,共需185元,那么购买甲、乙、丙三种商品各一件共需________元.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)解方程组:
(1) (2)
18.(8分)已知关于x,y的方程组
(1)若x的值比y的值小5,求m的值;
(2)若方程组的解也是方程3x+2y=17的一组解,求m的值.
19.(8分)已知关于x,y的方程组甲、乙二人解此方程组,甲正确地解出而乙把c抄错了,结果解得求a,b,c的值.
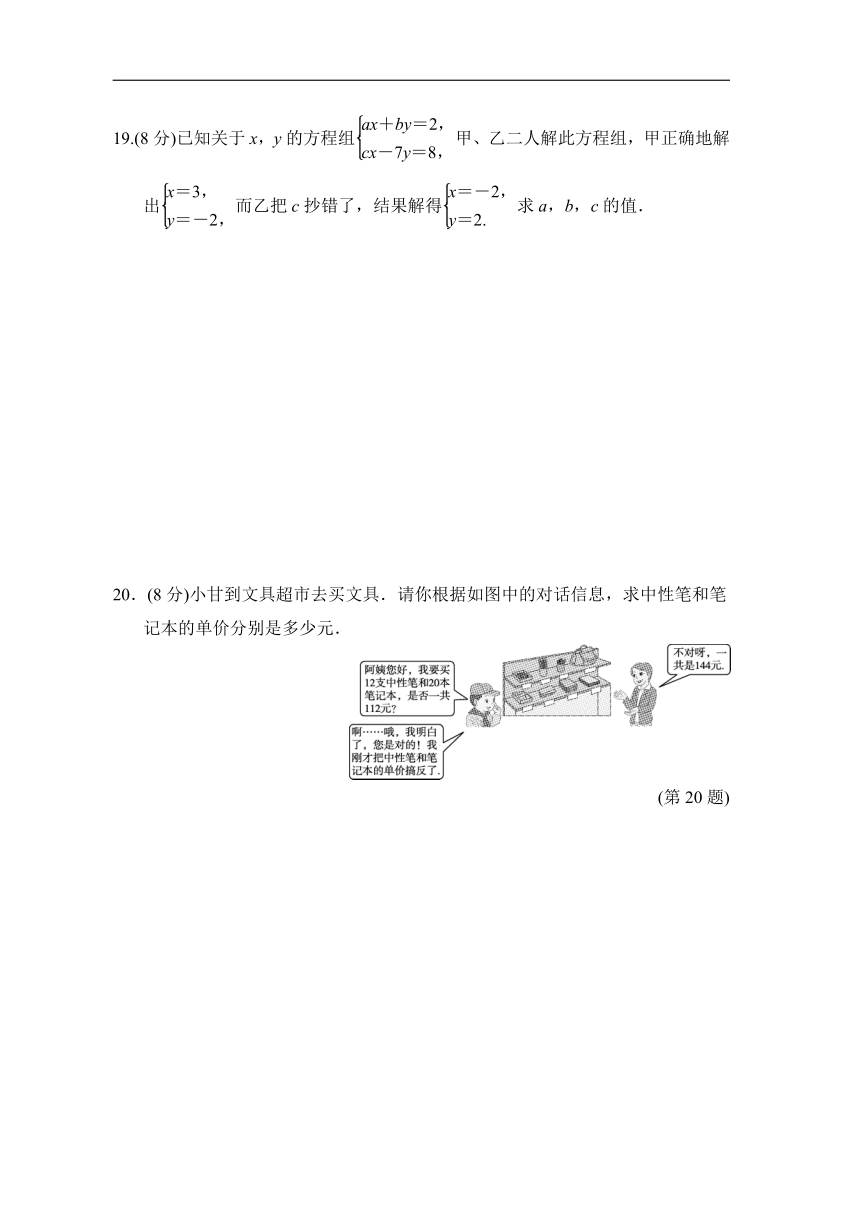
20.(8分)小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元.
INCLUDEPICTURE"+2.tif" INCLUDEPICTURE "D:\\方正转Word\\7HS福建\\+2.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\福建\\7HS福建\\+2.tif" \* MERGEFORMATINET
(第20题)
21.(10分)随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按p元/千米计算,耗时费按q元/分计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与车速如下表:
车速y(千米/时) 里程数s(千米) 车费(元)
小明 60 8 12
小刚 50 10 16
(1)求p,q的值;
(2)如果小华也用该打车方式,车速为55千米/时,行驶了11千米,那么小华的打车总费用为多少?
22.(10分)阅读下列材料,并填空.
问题:某班在购买啦啦操比赛的物资时,准备购买红色、黄色、蓝色三种颜色的啦啦操手花球,其颜色不同则价格不同.第一次买了15对红色啦啦操手花球、7对黄色啦啦操手花球、11对蓝色啦啦操手花球共用1 084元,第二次买了2对红色啦啦操手花球、4对黄色啦啦操手花球、3对蓝色啦啦操手花球共用304元,试问第三次购买红、黄、蓝色啦啦操手花球各一对共需多少元?(假定三次购买红、黄、蓝色啦啦操手花球单价不变)
解:设购买红、黄、蓝色啦啦操手花球的单价分别为x元,y元,z元,依题意得
上述方程组可变形为
设x+y+z=m,2x+z=n,上述方程组又可化为
①+4×②,得m=________,即x+y+z=________.
答:第三次购买红、黄、蓝色啦啦操手花球各一对共需________元.
阅读后,细心的你,可以解决下列问题:
某同学买13支黑笔、5支红笔、9个笔记本,共用去92.5元;买2支黑笔、4支红笔、3个笔记本,共用去32元,试问购买1支黑笔、1支红笔、1个笔记本共需多少钱?
答案
一、1.B 2.B 3.D 4.B 5.C 6.A 7.A
8.B 点拨:设2 m长的钢管有b根,根据题意,得a+2b=9.
∵a,b均为正整数,∴
故选B.
9.D 10.D
二、11.5x-7 12.答案不唯一,如: 13.-2
14.-7 15. 16.100
三、17.解:(1)
由①,得y=3x-7.③
把③代入②,得x+3(3x-7)=-1,解得x=2.
把x=2代入①,得y=-1.
所以原方程组的解为
(2)
②-①,得3x+3y=0.④
③-①,得24x+6y=60.⑤
由④⑤得方程组解得
把代入①,得z=-.所以
18.解:(1)由已知得x-y=-5,∴9m=-5,∴m=-.
(2)∵方程3x+2y=17的一组解与原方程组的解相同,
∴可得三元一次方程组解得m=1.
19.解:根据甲正确地解出将此解代入原方程组,根据乙仅因抄错了题中的c,解得将此解代入ax+by=2,
得解得
20.解:设中性笔和笔记本的单价分别是x元,y元,根据题意可得解得
答:中性笔和笔记本的单价分别是2元,6元.
21.解:(1)小明的里程数是8千米,时间为60×=8(分钟),小刚的里程数是10千米,时间为60×=12(分钟),
由题意得解得
(2)小华的里程数是11千米,时间为60×=12(分钟).
则11×1+12×=17(元).
答:小华的打车总费用为17元.
22.解:100;100;100
设购买1支黑笔需要x元,购买1支红笔需要y元,购买1个笔记本需要z元,依题意得
上述方程组可变形为
设x+y+z=m,2x+z=n,
上述方程组又可化为
①+4×②,得m=10.5,即x+y+z=10.5.
答:购买1支黑笔、1支红笔、1个笔记本共需10.5元.
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下列方程中,是二元一次方程的是( )
A.8x2+1=y B.y=8x+1 C.y= D.xy=1
2.若是关于x,y的方程ax-y=3的解,则a的值是( )
A.1 B.2 C.3 D.4
3.表格中上下每对x,y的值都是同一个二元一次方程的解,则这个方程为( )
x -1 0 1 2
y 8 5 2 -1
A.5x+y=3 B.x+y=5
C.2x-y=0 D.3x+y=5
4.已知(x-y-3)2+|x+y-1|=0,则yx的值为( )
A.-1 B.1 C.-2 D.2
5.若方程组的解是二元一次方程3x-5y-90=0的一个解,则a的值是( )
A.3 B.2 C.6 D.7
6.关于x,y的方程组的解是其中y的值被盖住了,不过仍能求出p,则p的值是( )
A.- B. C.- D.
7.如图,在某张桌子上放相同的木块,图中R=38 cm,S=102 cm,则桌子的高度是( )
INCLUDEPICTURE"1.tif" INCLUDEPICTURE "D:\\方正转Word\\7HS福建\\1.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\福建\\7HS福建\\1.tif" \* MERGEFORMATINET
(第7题)
A.70 cm B.50 cm C.65 cm D.14 cm
8.把一根9 m长的钢管截成1 m长和2 m长两种规格均有的短钢管,且没有余料,设某截法中1 m长的钢管有a根,则a的值可能有( )
A.3种 B.4种 C.5种 D.9种
9.我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:“甲乙隔沟牧放,二人暗里参详.甲云得乙九只羊,多乙一倍之上.乙说得甲九只,两家之数相当.二人闲坐恼心肠,画地算了半晌.”翻译成现代文,其大意如下:甲乙两人隔一条沟放牧,二人心里暗中合计.甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.请问甲乙各有多少只羊呢?设甲有羊x只,乙有羊y只,则符合题意的方程组是( )
A. B.
C. D.
10.小明说为方程ax+by=10的解,小慧说为方程ax+by=10的解,两人谁也不能说服对方,如果你想让他们的解都正确,则需要添加的条件是( )
A.a=12,b=10 B.a=9,b=10
C.a=10,b=11 D.a=10,b=10
二、填空题(本题共6小题,每小题3分,共18分)
11.已知方程5x-y=7,用含x的代数式表示y,y=________.
12.写一个以为解的二元一次方程组:________.
13.已知(a-2)x|a|-1+3y=1是关于x,y的二元一次方程,则a=________.
14.定义一种新运算“※”,规定:a※b=+.已知1※2=8,(-2)※3=4,则3※(-4)等于________.
15.甲袋中装有黄金9枚(每枚黄金质量相同),乙袋中装有白银11枚(每枚白银质量相同),两袋质量相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子的质量忽略不计),问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意可列方程组为______________.
16.甲、乙、丙三种商品,若购买甲商品3件、乙商品2件、丙商品1件,共需215元,购买甲商品1件、乙商品2件、丙商品3件,共需185元,那么购买甲、乙、丙三种商品各一件共需________元.
三、解答题(本题共6小题,共52分.解答应写出文字说明、证明过程或演算步骤)
17.(8分)解方程组:
(1) (2)
18.(8分)已知关于x,y的方程组
(1)若x的值比y的值小5,求m的值;
(2)若方程组的解也是方程3x+2y=17的一组解,求m的值.
19.(8分)已知关于x,y的方程组甲、乙二人解此方程组,甲正确地解出而乙把c抄错了,结果解得求a,b,c的值.
20.(8分)小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元.
INCLUDEPICTURE"+2.tif" INCLUDEPICTURE "D:\\方正转Word\\7HS福建\\+2.tif" \* MERGEFORMATINET INCLUDEPICTURE "E:\\22春\\福建\\7HS福建\\+2.tif" \* MERGEFORMATINET
(第20题)
21.(10分)随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按p元/千米计算,耗时费按q元/分计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与车速如下表:
车速y(千米/时) 里程数s(千米) 车费(元)
小明 60 8 12
小刚 50 10 16
(1)求p,q的值;
(2)如果小华也用该打车方式,车速为55千米/时,行驶了11千米,那么小华的打车总费用为多少?
22.(10分)阅读下列材料,并填空.
问题:某班在购买啦啦操比赛的物资时,准备购买红色、黄色、蓝色三种颜色的啦啦操手花球,其颜色不同则价格不同.第一次买了15对红色啦啦操手花球、7对黄色啦啦操手花球、11对蓝色啦啦操手花球共用1 084元,第二次买了2对红色啦啦操手花球、4对黄色啦啦操手花球、3对蓝色啦啦操手花球共用304元,试问第三次购买红、黄、蓝色啦啦操手花球各一对共需多少元?(假定三次购买红、黄、蓝色啦啦操手花球单价不变)
解:设购买红、黄、蓝色啦啦操手花球的单价分别为x元,y元,z元,依题意得
上述方程组可变形为
设x+y+z=m,2x+z=n,上述方程组又可化为
①+4×②,得m=________,即x+y+z=________.
答:第三次购买红、黄、蓝色啦啦操手花球各一对共需________元.
阅读后,细心的你,可以解决下列问题:
某同学买13支黑笔、5支红笔、9个笔记本,共用去92.5元;买2支黑笔、4支红笔、3个笔记本,共用去32元,试问购买1支黑笔、1支红笔、1个笔记本共需多少钱?
答案
一、1.B 2.B 3.D 4.B 5.C 6.A 7.A
8.B 点拨:设2 m长的钢管有b根,根据题意,得a+2b=9.
∵a,b均为正整数,∴
故选B.
9.D 10.D
二、11.5x-7 12.答案不唯一,如: 13.-2
14.-7 15. 16.100
三、17.解:(1)
由①,得y=3x-7.③
把③代入②,得x+3(3x-7)=-1,解得x=2.
把x=2代入①,得y=-1.
所以原方程组的解为
(2)
②-①,得3x+3y=0.④
③-①,得24x+6y=60.⑤
由④⑤得方程组解得
把代入①,得z=-.所以
18.解:(1)由已知得x-y=-5,∴9m=-5,∴m=-.
(2)∵方程3x+2y=17的一组解与原方程组的解相同,
∴可得三元一次方程组解得m=1.
19.解:根据甲正确地解出将此解代入原方程组,根据乙仅因抄错了题中的c,解得将此解代入ax+by=2,
得解得
20.解:设中性笔和笔记本的单价分别是x元,y元,根据题意可得解得
答:中性笔和笔记本的单价分别是2元,6元.
21.解:(1)小明的里程数是8千米,时间为60×=8(分钟),小刚的里程数是10千米,时间为60×=12(分钟),
由题意得解得
(2)小华的里程数是11千米,时间为60×=12(分钟).
则11×1+12×=17(元).
答:小华的打车总费用为17元.
22.解:100;100;100
设购买1支黑笔需要x元,购买1支红笔需要y元,购买1个笔记本需要z元,依题意得
上述方程组可变形为
设x+y+z=m,2x+z=n,
上述方程组又可化为
①+4×②,得m=10.5,即x+y+z=10.5.
答:购买1支黑笔、1支红笔、1个笔记本共需10.5元.
