3.5 确定圆的条件 课件(共20张PPT)
文档属性
| 名称 | 3.5 确定圆的条件 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 59.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览



文档简介
(共20张PPT)
北师版九年级下册 圆
§3.5 圆周角与圆心角的关系
1.了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法.
2.了解三角形的外接圆、三角形的外心等概念并会简单应用.
3.经历不在同一直线上的若干个点确定一个圆的探索过程,培养学生的探索能力.
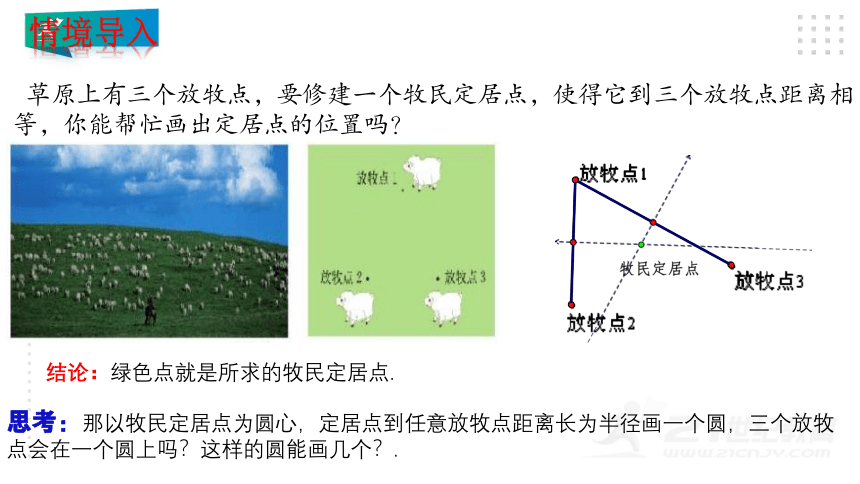
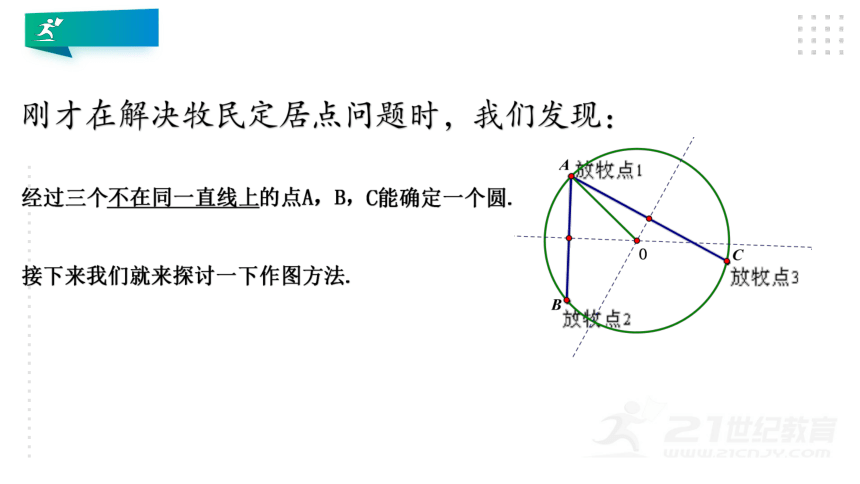
草原上有三个放牧点,要修建一个牧民定居点,使得它到三个放牧点距离相等,你能帮忙画出定居点的位置吗?
情境导入
结论:绿色点就是所求的牧民定居点.
思考:那以牧民定居点为圆心,定居点到任意放牧点距离长为半径画一个圆,三个放牧点会在一个圆上吗?这样的圆能画几个?.
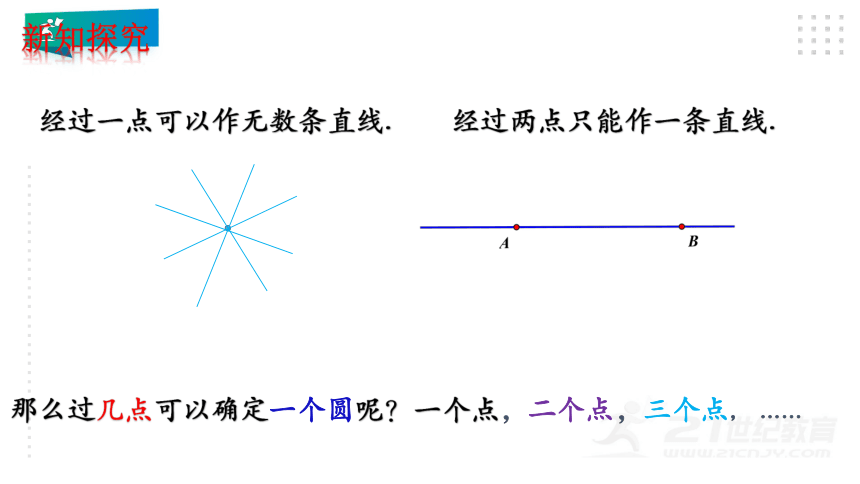
经过两点只能作一条直线.
经过一点可以作无数条直线.
新知探究
那么过几点可以确定一个圆呢?一个点,二个点,三个点, ......
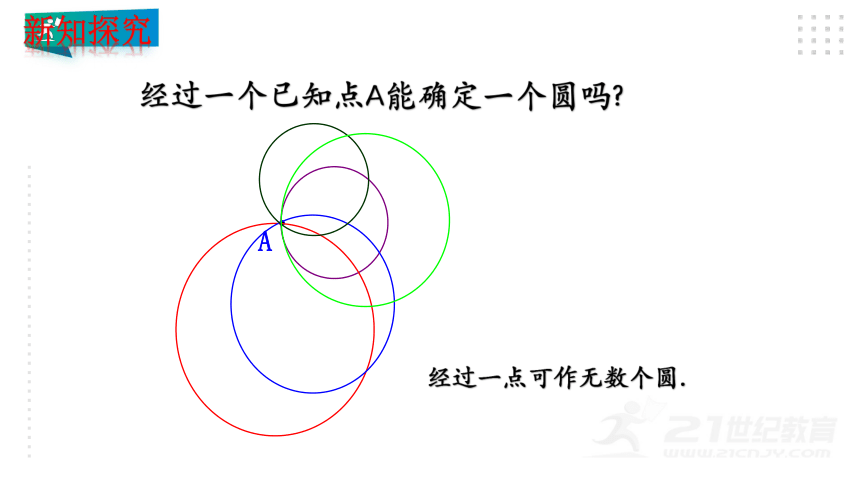
经过一个已知点A能确定一个圆吗
A
经过一点可作无数个圆.
新知探究
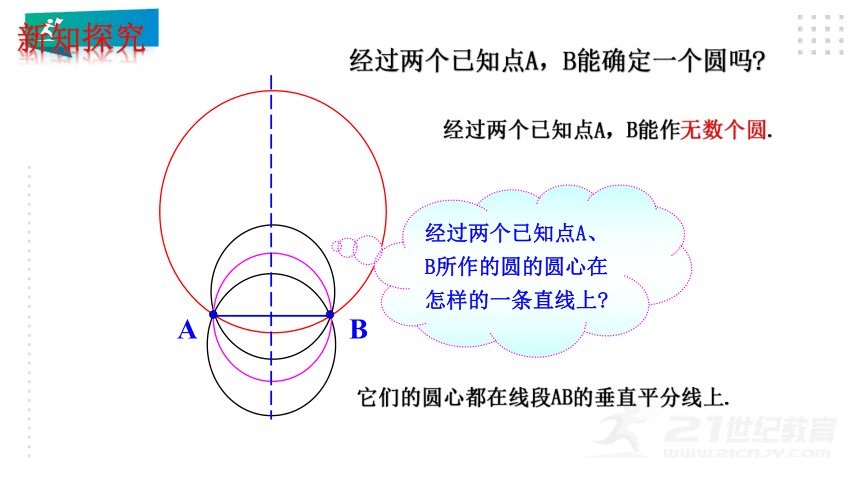
经过两个已知点A,B能确定一个圆吗
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的垂直平分线上.
经过两个已知点A,B能作无数个圆.
新知探究
过已知点A,B作圆,可以作无数个圆.
1.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
2.以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
你准备如何(确定圆心,半径)作圆?
其圆心的分布有什么特点 与线段AB有什么关系?
●A
●B
●O
●O
●O
●O
结论:
新知探究
刚才在解决牧民定居点问题时,我们发现:
经过三个不在同一直线上的点A,B,C能确定一个圆.
接下来我们就来探讨一下作图方法.
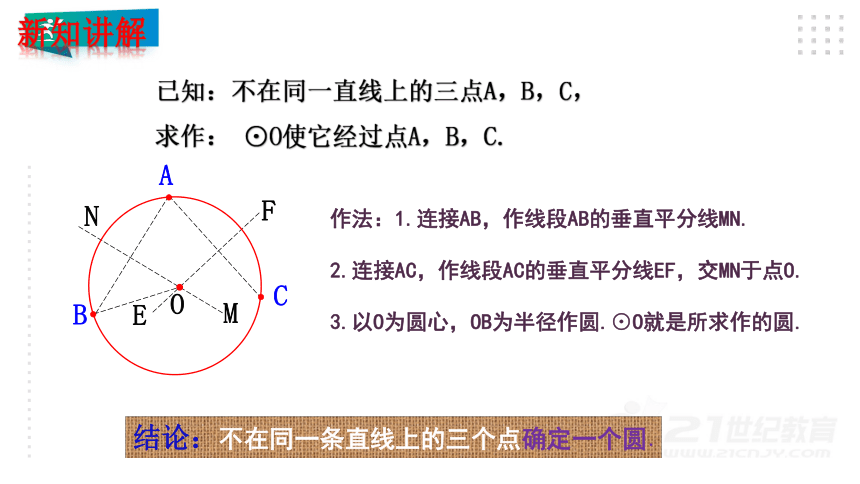
已知:不在同一直线上的三点A,B,C,
求作: ⊙O使它经过点A,B,C.
作法:1.连接AB,作线段AB的垂直平分线MN.
2.连接AC,作线段AC的垂直平分线EF,交MN于点O.
3.以O为圆心,OB为半径作圆.⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
新知讲解
结论:不在同一条直线上的三个点确定一个圆.
A
B
C
过如下三点能不能作一个圆 为什么
新知讲解
结论:如果三点在一条直线上,无法做圆.
新知讲解
三角形的外接圆
因此,三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆(circumcircle of triangle),外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心(circumcenter ).
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,
点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
你能确定一个圆形纸片的圆心吗 你有哪些方法 与同伴进行交流.
合作探究
方法一:将一个圆形纸片两次对折,其交点就是圆心的位置;
方法二:将一个直角三角板的直角顶点分两次放在圆周的不同位置上,画出斜边所在的直线,两条直线的交点即是圆心的位置;
方法三:尺规作图来确定圆心位置;
新知探究
已知下面的三个三角形,分别作出它们的外接圆.它们外心的位置有怎样的特点
外心在三角形内部
外心在三角形斜边上
外心在三角形外部
跟踪练习
1.下列条件,可以画出唯一一个圆的是( )
A.已知圆心 B.已知半径
C.已知直径 D.已知不在同一条直线上的三个点
2.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
D
B
3.在同一平面上有A,B,C三点,若经过A,B,C这三点画圆,则可画( )
A.0个 B.1个
C.0个或1个 D.无数个
C
4.如图,⊙O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
A.22° B.26° C.32° D.68°
A
跟踪练习
1. 己知AB=4cm,以3cm长为半径作圆,使它经过点A和点B.这样的圆能作出几个
2. 经过不在同一条直线上的四个点是否一定能作一个圆"举例说明.
解析:如图,以O1为圆心,O1A为半径可以画一个;再以O2为圆心,O2B为半径可以再画一个。一共两个.
解析:不一定,只有当四个点围成的四边形,其中一对儿对角互补时,四个点才能在同一个圆上.(如右图A,B,C,D)
拓展探究
3.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用
( )次,就可以找到圆形工件的圆心.
A、1 B、2 C、3 D、4
B
拓展探究
1.(2019·衡阳)如图,已知圆的半径是6,则圆内接正三角形的边长是 .
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
6√3
B
D
课堂练习
3.已知点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100°
C.40°或140° D.40°或100°
C
课堂练习
1.通过本课的学习,你有什么收获?还有什么问题?
2.确定圆的条件——
不在同一直线上的三点
圆心、半径
3. 锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边上
钝角三角形 在三角形的外部
北师版九年级下册 圆
§3.5 圆周角与圆心角的关系
1.了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法.
2.了解三角形的外接圆、三角形的外心等概念并会简单应用.
3.经历不在同一直线上的若干个点确定一个圆的探索过程,培养学生的探索能力.
草原上有三个放牧点,要修建一个牧民定居点,使得它到三个放牧点距离相等,你能帮忙画出定居点的位置吗?
情境导入
结论:绿色点就是所求的牧民定居点.
思考:那以牧民定居点为圆心,定居点到任意放牧点距离长为半径画一个圆,三个放牧点会在一个圆上吗?这样的圆能画几个?.
经过两点只能作一条直线.
经过一点可以作无数条直线.
新知探究
那么过几点可以确定一个圆呢?一个点,二个点,三个点, ......
经过一个已知点A能确定一个圆吗
A
经过一点可作无数个圆.
新知探究
经过两个已知点A,B能确定一个圆吗
A
B
经过两个已知点A、B所作的圆的圆心在怎样的一条直线上
它们的圆心都在线段AB的垂直平分线上.
经过两个已知点A,B能作无数个圆.
新知探究
过已知点A,B作圆,可以作无数个圆.
1.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
2.以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.
你准备如何(确定圆心,半径)作圆?
其圆心的分布有什么特点 与线段AB有什么关系?
●A
●B
●O
●O
●O
●O
结论:
新知探究
刚才在解决牧民定居点问题时,我们发现:
经过三个不在同一直线上的点A,B,C能确定一个圆.
接下来我们就来探讨一下作图方法.
已知:不在同一直线上的三点A,B,C,
求作: ⊙O使它经过点A,B,C.
作法:1.连接AB,作线段AB的垂直平分线MN.
2.连接AC,作线段AC的垂直平分线EF,交MN于点O.
3.以O为圆心,OB为半径作圆.⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
新知讲解
结论:不在同一条直线上的三个点确定一个圆.
A
B
C
过如下三点能不能作一个圆 为什么
新知讲解
结论:如果三点在一条直线上,无法做圆.
新知讲解
三角形的外接圆
因此,三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆(circumcircle of triangle),外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心(circumcenter ).
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,
点O是△ABC的外心
外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
C
A
B
O
你能确定一个圆形纸片的圆心吗 你有哪些方法 与同伴进行交流.
合作探究
方法一:将一个圆形纸片两次对折,其交点就是圆心的位置;
方法二:将一个直角三角板的直角顶点分两次放在圆周的不同位置上,画出斜边所在的直线,两条直线的交点即是圆心的位置;
方法三:尺规作图来确定圆心位置;
新知探究
已知下面的三个三角形,分别作出它们的外接圆.它们外心的位置有怎样的特点
外心在三角形内部
外心在三角形斜边上
外心在三角形外部
跟踪练习
1.下列条件,可以画出唯一一个圆的是( )
A.已知圆心 B.已知半径
C.已知直径 D.已知不在同一条直线上的三个点
2.如图,在5×5的正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是( )
A.点P
B.点Q
C.点R
D.点M
D
B
3.在同一平面上有A,B,C三点,若经过A,B,C这三点画圆,则可画( )
A.0个 B.1个
C.0个或1个 D.无数个
C
4.如图,⊙O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
A.22° B.26° C.32° D.68°
A
跟踪练习
1. 己知AB=4cm,以3cm长为半径作圆,使它经过点A和点B.这样的圆能作出几个
2. 经过不在同一条直线上的四个点是否一定能作一个圆"举例说明.
解析:如图,以O1为圆心,O1A为半径可以画一个;再以O2为圆心,O2B为半径可以再画一个。一共两个.
解析:不一定,只有当四个点围成的四边形,其中一对儿对角互补时,四个点才能在同一个圆上.(如右图A,B,C,D)
拓展探究
3.如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用
( )次,就可以找到圆形工件的圆心.
A、1 B、2 C、3 D、4
B
拓展探究
1.(2019·衡阳)如图,已知圆的半径是6,则圆内接正三角形的边长是 .
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
6√3
B
D
课堂练习
3.已知点O是△ABC的外心,若∠BOC=80°,则∠BAC的度数为( )
A.40° B.100°
C.40°或140° D.40°或100°
C
课堂练习
1.通过本课的学习,你有什么收获?还有什么问题?
2.确定圆的条件——
不在同一直线上的三点
圆心、半径
3. 锐角三角形 在三角形的内部
直角三角形 --外心的位置--- 在斜边上
钝角三角形 在三角形的外部
