3.4.2 圆周角与圆心角的关系 课件(共21张PPT)
文档属性
| 名称 | 3.4.2 圆周角与圆心角的关系 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 64.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览





文档简介
(共21张PPT)
北师版九年级下册 圆
§3.4.2 圆周角与圆心角的关系
1.进一步探索直径所对的圆周角的特征,并能应用其进行简单的计算与证
明.(重点)
2.掌握圆内接四边形的有关概念及推论.(难点)
3、引导学生掌握两种常用的解题方法:
(1)善于寻找(构造)同弧所对圆周角;(2)“见直径,构造直角三角形”
要点回顾
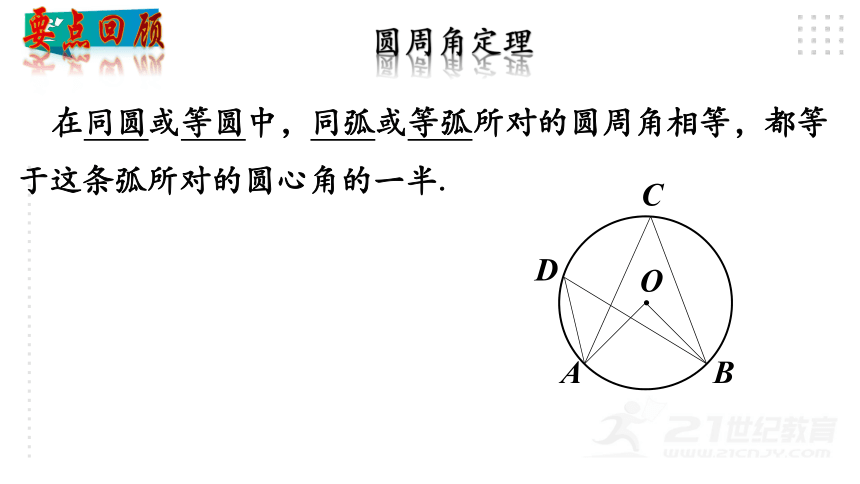
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
·
C
D
A
B
O
1.如图(1),BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗
2.如图(2),圆周角∠BAC =90 ,弦BC经过圆心O吗?为什么?
B
C
O
A
图(1)
F
E
●
B
C
A
图(2)
O
合作探究
圆周角定理的推论2
直径所对的圆周角是直角;90°的圆周角所对的弦是直径.(如下图)
新知讲解
A
O
B
C1
C2
C3
归纳总结
推论1:同弧或等弧所对的圆周角相等;
推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
推论:
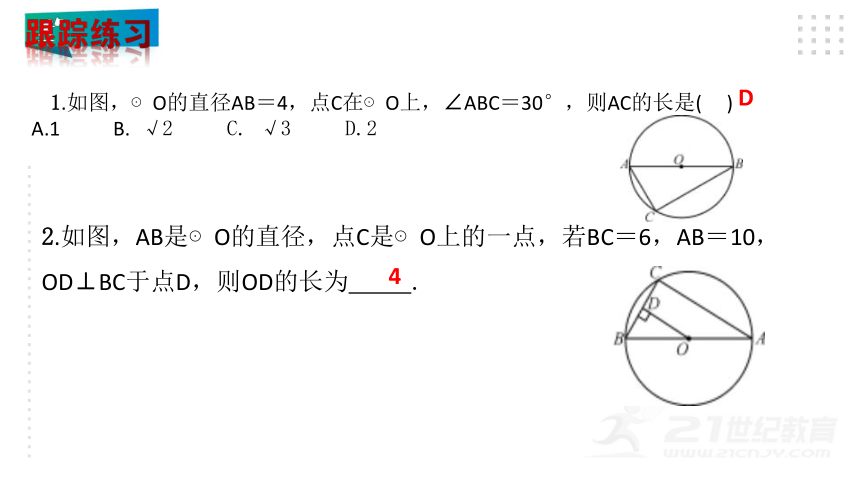
1.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是( )
A.1 B. √2 C. √3 D.2
2.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
D
4
跟踪练习
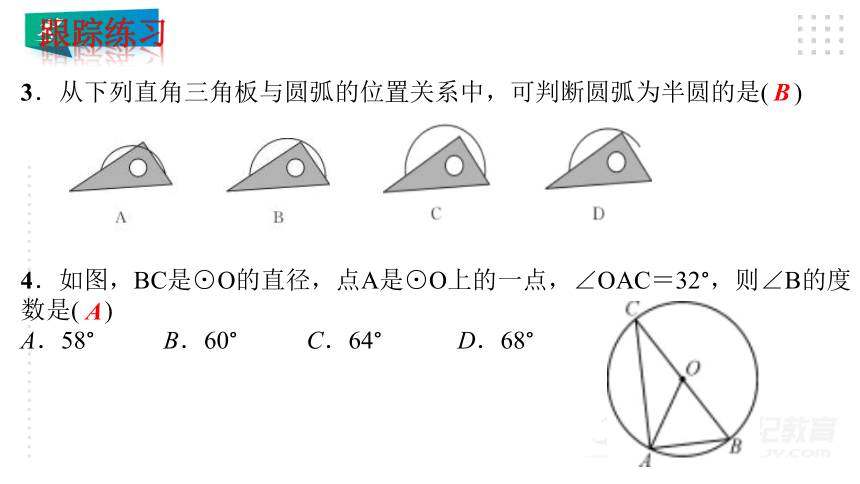
3.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
4.如图,BC是⊙O的直径,点A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )
A.58° B.60° C.64° D.68°
B
A
跟踪练习
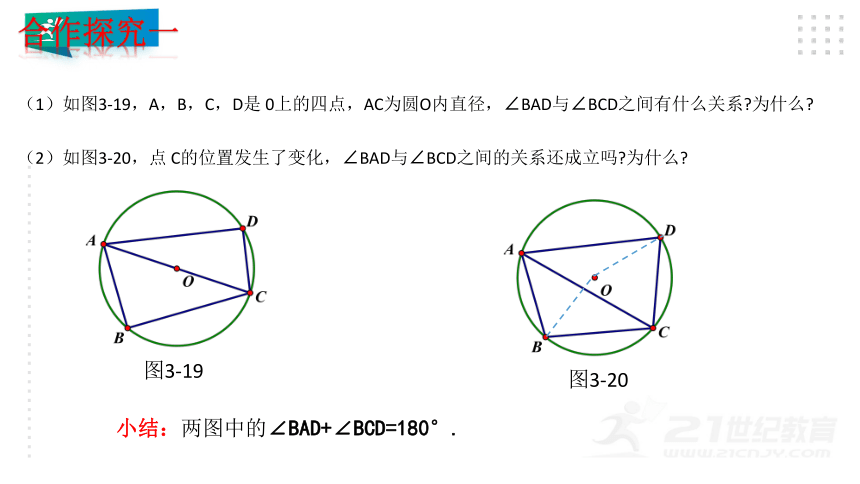
(1)如图3-19,A,B,C,D是 0上的四点,AC为圆O内直径,∠BAD与∠BCD之间有什么关系 为什么
(2)如图3-20,点 C的位置发生了变化,∠BAD与∠BCD之间的关系还成立吗 为什么
图3-19
图3-20
合作探究一
小结:两图中的∠BAD+∠BCD=180°.
在图3-19、图3-20中,四边形ABCD的四个顶点都在圆O上,
像这样的四边形叫做圆内接四边形(inscribed quadrilateral),
这个圆叫做四边形的外接圆∶
新知讲解
推论1:圆内接四边形对角互补.
如图3-21,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有什么关系
合作探究二
解:∵四边形ABCD为圆O的内接四边形
∴∠A+∠BCD=180°.
又∵∠DCE+∠BCD=180°.
∴∠DCE=∠A.
推论2:任何一个外角都等于它的内对角。
图3-21
1.如图,在⊙O的内接四边形ABCD中,∠BCD=110°,则∠BOD= .
140°
跟踪练习
2.如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为
4∶3∶5,∠D的度数是 .
120°
4.(2020·盐城)如图,在⊙O中,点A在弧BC上,∠BOC=100°,则∠BAC= .
130°
3.(2020·聊城)如图,在⊙O中,四边形OABC为菱形,点D在弧AmC上,则∠ADC的度数是 .
60°
跟踪练习
1.(10分)如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.求⊙C的半径.
解:∵四边形ABMO内接于⊙C,
∴∠BAO+∠BMO=180°.
∵∠BMO=120°,
∴∠BAO=60°.
在Rt△ABO中,AO=4,∠BAO=60°,∴AB=8.
∵∠AOB=90°,
∴AB为⊙C的直径.
∴⊙C的半径为4.
综合提升
2.如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=
,AC=5,AD=4,求⊙O的直径AE.
综合提升
解析∶由圆周角定理可知,∠E=∠C.
∵∠ABE=∠ADC=90°,∠E= ∠C, ∴△ABE∽△ADC,AB:AD=AE:AC.
∵AB=4√2,AC=5,AD=4, 4√2:4=AE:5.
AE=5√2.
(2019·河南)如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是弧BD上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:△ADF≌△BDG;
(2)填空:
①若AB=4,且点E是弧BD的中点,则DF的长为 ;
②取弧AE的中点H,当∠EAB的度数为 时,四边形OBEH为菱形.
中考实战
(1)求证:△ADF≌△BDG;
解析:由题意可知:
因为AB为直径,所以∠AEB=∠ADB=∠GDB=90°
又因为∠ABC=90°,AB=AC,所以∠DAB=45°,所以AD=DB.又因为∠DAF=∠DBG.
因此可证△ADF≌△BDG
证明 略
①若AB=4,且点E是弧BD的中点,则DF的长为 ;
解析:在等腰直角三角形ADB中
因为AB=4,所以AD=DB=2√2
因为E为弧DB的中点,所以∠GAE=∠BAE.又因为AE⊥GB
所以△GAB为等腰三角形,AG=AB.
所以DF=DG=4-2√2
②取弧AE的中点H,当∠EAB的度数为 时,四边形OBEH为菱形.
H
解析:如右图,连接OE.
若四边形OBEH是菱形,则OB=EB,又因为OE=OB,所以△OEB是等边三角形.∠EBA=60°
所以∠EAB=90°-∠EAB=30°.
18.(9分)(2016 河南)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;(2)填空:
①若AB=6,当AD=2DM时,DE= ;
②连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
中考实战
【点评】本题考查圆内接四边形性质、直角三角形斜边中线性质、菱形的判定等知识,解题的关键是灵活运用这些知识解决问题,记住菱形的三种判定方法,属于中考常考题型.
2
60°
1.要理解好圆周角定理的推论.
2.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:
(1)构造直径上的圆周角.
(2)构造(寻找)同弧所对的圆周角.
3.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周角也是常用方法之一.
北师版九年级下册 圆
§3.4.2 圆周角与圆心角的关系
1.进一步探索直径所对的圆周角的特征,并能应用其进行简单的计算与证
明.(重点)
2.掌握圆内接四边形的有关概念及推论.(难点)
3、引导学生掌握两种常用的解题方法:
(1)善于寻找(构造)同弧所对圆周角;(2)“见直径,构造直角三角形”
要点回顾
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
·
C
D
A
B
O
1.如图(1),BC是⊙O的直径,A是⊙O上任一点,你能确定∠BAC的度数吗
2.如图(2),圆周角∠BAC =90 ,弦BC经过圆心O吗?为什么?
B
C
O
A
图(1)
F
E
●
B
C
A
图(2)
O
合作探究
圆周角定理的推论2
直径所对的圆周角是直角;90°的圆周角所对的弦是直径.(如下图)
新知讲解
A
O
B
C1
C2
C3
归纳总结
推论1:同弧或等弧所对的圆周角相等;
推论2:直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
推论:
1.如图,⊙O的直径AB=4,点C在⊙O上,∠ABC=30°,则AC的长是( )
A.1 B. √2 C. √3 D.2
2.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
D
4
跟踪练习
3.从下列直角三角板与圆弧的位置关系中,可判断圆弧为半圆的是( )
4.如图,BC是⊙O的直径,点A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )
A.58° B.60° C.64° D.68°
B
A
跟踪练习
(1)如图3-19,A,B,C,D是 0上的四点,AC为圆O内直径,∠BAD与∠BCD之间有什么关系 为什么
(2)如图3-20,点 C的位置发生了变化,∠BAD与∠BCD之间的关系还成立吗 为什么
图3-19
图3-20
合作探究一
小结:两图中的∠BAD+∠BCD=180°.
在图3-19、图3-20中,四边形ABCD的四个顶点都在圆O上,
像这样的四边形叫做圆内接四边形(inscribed quadrilateral),
这个圆叫做四边形的外接圆∶
新知讲解
推论1:圆内接四边形对角互补.
如图3-21,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有什么关系
合作探究二
解:∵四边形ABCD为圆O的内接四边形
∴∠A+∠BCD=180°.
又∵∠DCE+∠BCD=180°.
∴∠DCE=∠A.
推论2:任何一个外角都等于它的内对角。
图3-21
1.如图,在⊙O的内接四边形ABCD中,∠BCD=110°,则∠BOD= .
140°
跟踪练习
2.如图,在圆内接四边形ABCD中,若∠A,∠B,∠C的度数之比为
4∶3∶5,∠D的度数是 .
120°
4.(2020·盐城)如图,在⊙O中,点A在弧BC上,∠BOC=100°,则∠BAC= .
130°
3.(2020·聊城)如图,在⊙O中,四边形OABC为菱形,点D在弧AmC上,则∠ADC的度数是 .
60°
跟踪练习
1.(10分)如图,⊙C经过坐标原点,且与两坐标轴分别交于点A与点B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.求⊙C的半径.
解:∵四边形ABMO内接于⊙C,
∴∠BAO+∠BMO=180°.
∵∠BMO=120°,
∴∠BAO=60°.
在Rt△ABO中,AO=4,∠BAO=60°,∴AB=8.
∵∠AOB=90°,
∴AB为⊙C的直径.
∴⊙C的半径为4.
综合提升
2.如图,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=
,AC=5,AD=4,求⊙O的直径AE.
综合提升
解析∶由圆周角定理可知,∠E=∠C.
∵∠ABE=∠ADC=90°,∠E= ∠C, ∴△ABE∽△ADC,AB:AD=AE:AC.
∵AB=4√2,AC=5,AD=4, 4√2:4=AE:5.
AE=5√2.
(2019·河南)如图,在△ABC中,BA=BC,∠ABC=90°,以AB为直径的半圆O交AC于点D,点E是弧BD上不与点B,D重合的任意一点,连接AE交BD于点F,连接BE并延长交AC于点G.
(1)求证:△ADF≌△BDG;
(2)填空:
①若AB=4,且点E是弧BD的中点,则DF的长为 ;
②取弧AE的中点H,当∠EAB的度数为 时,四边形OBEH为菱形.
中考实战
(1)求证:△ADF≌△BDG;
解析:由题意可知:
因为AB为直径,所以∠AEB=∠ADB=∠GDB=90°
又因为∠ABC=90°,AB=AC,所以∠DAB=45°,所以AD=DB.又因为∠DAF=∠DBG.
因此可证△ADF≌△BDG
证明 略
①若AB=4,且点E是弧BD的中点,则DF的长为 ;
解析:在等腰直角三角形ADB中
因为AB=4,所以AD=DB=2√2
因为E为弧DB的中点,所以∠GAE=∠BAE.又因为AE⊥GB
所以△GAB为等腰三角形,AG=AB.
所以DF=DG=4-2√2
②取弧AE的中点H,当∠EAB的度数为 时,四边形OBEH为菱形.
H
解析:如右图,连接OE.
若四边形OBEH是菱形,则OB=EB,又因为OE=OB,所以△OEB是等边三角形.∠EBA=60°
所以∠EAB=90°-∠EAB=30°.
18.(9分)(2016 河南)如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;(2)填空:
①若AB=6,当AD=2DM时,DE= ;
②连接OD,OE,当∠A的度数为 时,四边形ODME是菱形.
中考实战
【点评】本题考查圆内接四边形性质、直角三角形斜边中线性质、菱形的判定等知识,解题的关键是灵活运用这些知识解决问题,记住菱形的三种判定方法,属于中考常考题型.
2
60°
1.要理解好圆周角定理的推论.
2.构造直径所对的圆周角是圆中的常用方法.引辅助线的方法:
(1)构造直径上的圆周角.
(2)构造(寻找)同弧所对的圆周角.
3.要多观察图形,善于识别圆周角与圆心角,构造同弧所对的圆周角也是常用方法之一.
