2021-2022学年青岛版七年级上册数学 第5章 代数式与函数的初步认识 单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年青岛版七年级上册数学 第5章 代数式与函数的初步认识 单元测试卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览



文档简介
2021-2022学年青岛新版七年级上册数学《第5章 代数式与函数的初步认识》单元测试卷
一.选择题
1.在下列各式中,不是代数式的是( )
A.7 B.3>2 C. D. x2+y2
2.已知代数式x+2y的值是2,则代数式1﹣2x﹣4y的值是( )
A.﹣1 B.﹣3 C.﹣5 D.﹣8
3.在圆的周长计算公式C=2πR中,对于变量和常量的说法正确的是( )
A.2是常量,C,π,R是变量 B.2,π是常量,C,R是变量
C.2,C,π是常量,R是变量 D.2,π,R是常量,C是变量
4.已知6头大象1天的食品可供500只老鼠吃300天,假定每头大象的食量都一样,每只老鼠的食量也相等,那么t头大象1天的食品可供100只老鼠吃( )天.
A.250t B.300t C.500t D.600t
5.已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )
A.31 B.﹣31 C.41 D.﹣41
6.代数式的意义是( )
A.x除以y加3
B.y加3除x
C.y与3的和除以x
D.x除以y与3的和所得的商
7.点O,A,B,C在数轴上的位置如图所示,其中O为原点,BC=2,OA=OB,若C点所表示的数为x,则A点所表示的数为( )
A.﹣x+2 B.﹣x﹣2 C.x+2 D.﹣2
8.将正整数按如图所示的规律排列,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示123的有序数对是( )
A.(16,3) B.(15,3) C.(16,14) D.(15,13)
9.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.0.6元/千瓦时是自变量,y是因变量
C.y是自变量,x是因变量
D.x是自变量,y是因变量,0.6元/千瓦时是常量
10.下列各式:①1x;②2 3;③20%x;④a﹣b÷c;⑤;⑥x﹣5;其中,不符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
二.填空题
11.下列各式:①1x;②2 3;③20%x;④a﹣b÷c;⑤;⑥x﹣5;其中,不符合代数式书写要求的有 (填写序号)
12.已知代数式m+2n=1,则代数式3m+6n+5的值为 .
13.如图,是一种数值转换机的运算程序.若输入的数为5,则第100次输出的数是 .
14.某超市的苹果价格如图,试说明代数式100﹣9.8x的实际意义 .
15.一个两位数,其十位数字是x,个位数字为y,则这个两位数可表示为: .
16.快餐每盒5元,买n盒需付m元,则其中常量是 .
17.观察下面的变化规律:=1﹣,=﹣,=,=,…根据上面的规律计算: +++…+= .
18.某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是 .
年份 第一年 第二年 第三年 第四年 第五年
分枝数 1 1 2 3 5
19.举例说明代数式8a3的意义: .
20.某种水果的售价为每千克a元(a≤30),用面值为100元的人民币购买了3千克这种水果,应找回 元(用含a的代数式表示).
三.解答题
21.说出下列代数式的意义:
(1)2(a+3);
(2)a2+b2;
(3).
22.为鼓励居民节约用水,某市自来水公司实施阶梯水价:如果每月用水不超过8吨,按每吨2.3元收费;如果每月用水量超过8吨,则超出部分按每吨3.5元收费,设每月用水量为x吨.
(1)当每月用水量不超过8吨时,用含x的代数式表示用水费用为 元;
(2)当每月用水超过8吨时,需交水费多少元?(用含x的代数式表示)
(3)若小红家8月份用水12吨,则需交水费多少元?
23.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、b、c满足(c﹣5)2+|a+b|=0.
(1)a= ,b= ,c= .
(2)若将数轴折叠,使得A点与C点重合,则点B与表示数 的点重合;
(3)点A、B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= (用含t的代数式表示)
(4)请问:3BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
24.(1)根据生活经验,对代数式3x+2y作出解释.
(2)两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
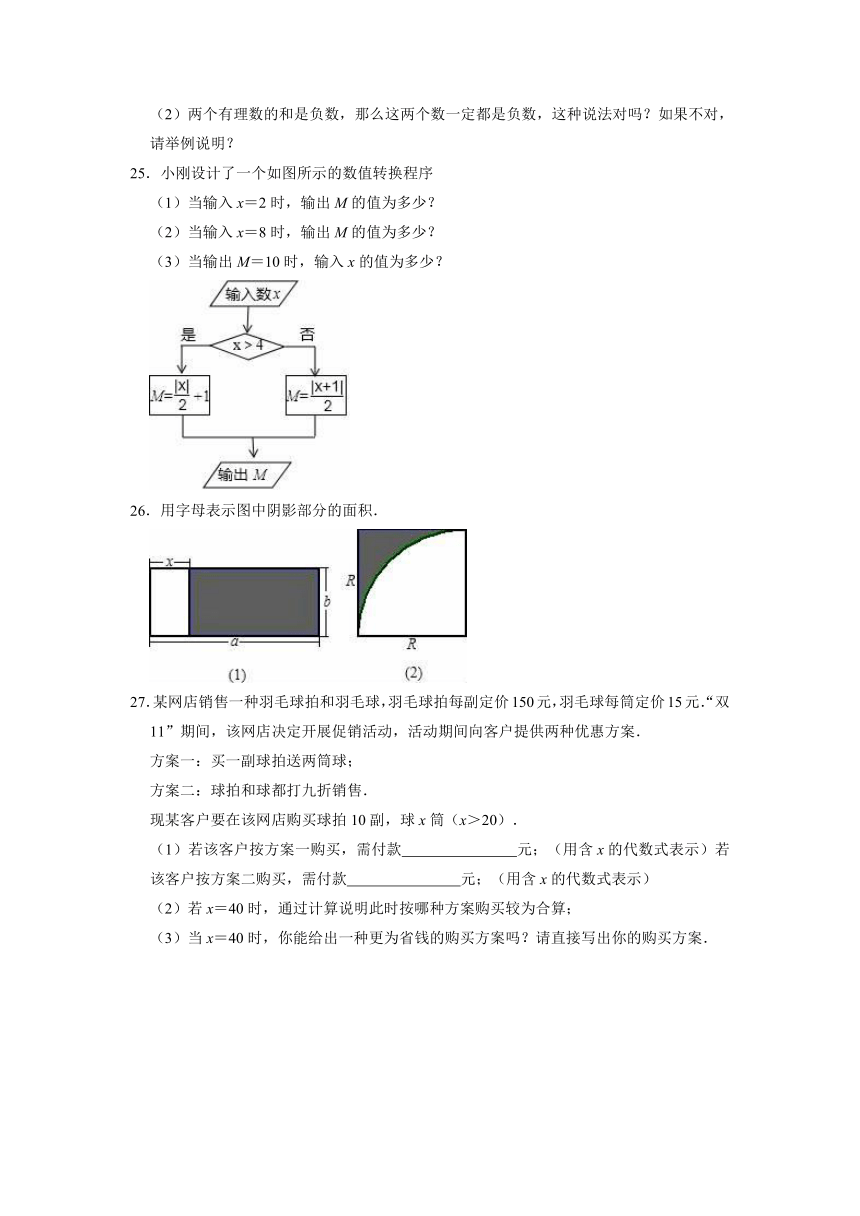
25.小刚设计了一个如图所示的数值转换程序
(1)当输入x=2时,输出M的值为多少?
(2)当输入x=8时,输出M的值为多少?
(3)当输出M=10时,输入x的值为多少?
26.用字母表示图中阴影部分的面积.
27.某网店销售一种羽毛球拍和羽毛球,羽毛球拍每副定价150元,羽毛球每筒定价15元.“双11”期间,该网店决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副球拍送两筒球;
方案二:球拍和球都打九折销售.
现某客户要在该网店购买球拍10副,球x筒(x>20).
(1)若该客户按方案一购买,需付款 元;(用含x的代数式表示)若该客户按方案二购买,需付款 元;(用含x的代数式表示)
(2)若x=40时,通过计算说明此时按哪种方案购买较为合算;
(3)当x=40时,你能给出一种更为省钱的购买方案吗?请直接写出你的购买方案.
参考答案与试题解析
一.选择题
1.解:A、C、D、是代数式,B是不等式,不是代数式.
故选:B.
2.解:根据题意得:
x+2y=2,
方程两边同时乘以﹣2得:﹣2x﹣4y=﹣4,
方程两边同时加上1得:1﹣2x﹣4y=1﹣4=﹣3,
故选:B.
3.解:在圆的周长计算公式C=2πR中,C和R是变量,2、π是常量,
故选:B.
4.解:∵6头大象1天的食品可供500只老鼠吃300天,
∴1头大象1天的食品可供500只老鼠吃50天,
∴t头大象1天的食品可供100只老鼠吃250t天.
故选:A.
5.解:∵x2﹣3x﹣12=0,
∴x2﹣3x=12.
原式=﹣3(x2﹣3x)+5=﹣3×12+5=﹣36+5=﹣31.
故选:B.
6.解:的意义是x除以y与3的和所得的商.
故选:D.
7.解:∵BC=2,C点所表示的数为x,
∴B点表示的数是x﹣2,
又∵OA=OB,
∴B点和A点表示的数互为相反数,
∴A点所表示的数是﹣(x﹣2),即﹣x+2.
故选:A.
8.解:由图可知,
第一排1个数,
第二排2个数,数字从大到小排列,
第三排3个数,数字从小到大排列,
第四排4个数,数字从大到小排列,
…,
则前n排的数字共有个数,
∵当n=15时,=120,
∴表示123的有序数对是(16,14),
故选:C.
9.解:在这个问题中,x是自变量,y是因变量,0.6元/千瓦时是常数.
故选:D.
10.解:①1x分数不能为带分数;
②2 3数与数相乘不能用“ ”;
③20%x,书写正确;
④a﹣b÷c不能出现除号;
⑤,书写正确;
⑥x﹣5,书写正确,
不符合代数式书写要求的有①②④共3个.
故选:C.
二.填空题
11.解:①1x分数不能为带分数;
②2 3数与数相乘不能用“ ”;
③20%x,书写正确;
④a﹣b÷c,书写错误;
⑤;书写正确;
⑥x﹣5,书写正确,
不符合代数式书写要求的有①②④共3个.
故答案为:①②④.
12.解:∵m+2n=1,
∴3m+6n+5=3(m+2n)+5=3×1+5=3+5=8.
故答案为:8.
13.解:当第1次输入的数为x=5时,
第一次输出5+3=8,
第二次输出8×=4,
第三次输出4×=2,
第四次输出2×=1,
第五次输出1+3=4,
除去前1次,以4,2,1循环,三个一循环,则第100次输出的数为1;
故答案为:1.
14.解:代数式100﹣9.8x的实际意义为:用100元买每斤9.8元的苹果x斤余下的钱.
故答案为:用100元买每斤9.8元的苹果x斤余下的钱.
15.解:根据两位数的表示方法得:
这个两位数表示为:10x+y.
故答案为:10x+y.
16.解:单价5元固定,是常量.
故答案为:5.
17.解:原式=1﹣+﹣+﹣+﹣+…+﹣
=1﹣
=.
故答案为:.
18.解:根据所给的具体数据发现:
从第三个数据开始,每一个数据是前面两个数据的和,则第6年的时候是3+5=8个.
自变量是年份,因变量是分枝数,
故答案为:8,年份,分枝数.
19.解:如一个正方体的棱长是a,一个正方体的体积是a3,那么8个正方体的体积是8a3.
故答案为:如一个正方体的棱长是a,一个正方体的体积是a3,那么8个正方体的体积是8a3.
20.解:∵购买这种售价是每千克a元的水果3千克需3a元,
∴根据题意,应找回(100﹣3a)元.
故答案为:(100﹣3a).
三.解答题
21.解:(1)2(a+3)的意义是2与(a+3)的积;
(2)a2+b2的意义是a,b的平方的和;
(3)的意义是(n+1)除以(n﹣1)的商.
22.解:(1)当x不超过8吨时,这个月的水费为:2.3x;
故答案为:2.3x.
(2)当x超过8吨时,
这个月的水费为:8×2.3+(x﹣8)×3.5=18.4+3.5x﹣28=3.5x﹣9.6,
∴需交水费(3.5x﹣9.6)元.
(3)当x=12时,
3.5×12﹣9.6=42﹣9.6=32.4(元)
∴用水12吨需交水费32.4元.
23.解:(1)∵(c﹣5)2+|a+b|=0,
∴a+b=0,c﹣5=0,
解得a=﹣b,c=5,
∵b是最小的正整数,
∴b=1;a=﹣1
故答案为:﹣1,1,5;
(2)点A与点C的中点对应的数为:=2,
点B到2的距离为1,所以与点B重合的数是:2+1=3.
故答案为:3;
(3)AB=t+2t+2=3t+2,AC=t+3t+6=4t+6,BC=t+4;
故答案为:3t+2,4t+6,t+4.
(4)∵3BC﹣AB=3(t+4)﹣(3t+2)=10,
∴3BC﹣AB的值不随着时间t的变化而改变,其值为10.
24.解:(1)根据生活经验,对代数式3x+2y作出解释.
某水果超市推出两款促销水果,其中苹果每斤x元,香蕉每斤y元,小明买了3斤苹果和2斤香蕉,共花去(3x+2y)元钱.
(2)两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
这种说法不正确,例如:﹣4+3=﹣1.
25.解:(1)当x=2时,M==;
(2)当x=8时,M=+1=5;
(3)若+1=10,则x=18或x=﹣18(舍);
若=10,则x=19(舍)或x=﹣21;
综上,当输出M=10时,输入x的值为18或﹣21.
26.解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2﹣πR2.
27.解:(1)根据题意,得
方案一:1500+15(x﹣20)=15x+1200
方案二:(150×10+15x)×90%=13.5x+1350
故答案为15x+1200;13.5x+1350.
(2)当x=40时,
方案一:15x+1200=15×40+1200=1800(元)
方案二:13.5x+1350=13.5×40+1350=1890(元)
∵1890>1800
∴按方案一购买较合算.
(3)先按方案一购买10副球拍获赠20筒球,再按方案二购买20筒球
则需付款1500+20×15×90%=1770(元),
比方案一和方案二都省钱.
一.选择题
1.在下列各式中,不是代数式的是( )
A.7 B.3>2 C. D. x2+y2
2.已知代数式x+2y的值是2,则代数式1﹣2x﹣4y的值是( )
A.﹣1 B.﹣3 C.﹣5 D.﹣8
3.在圆的周长计算公式C=2πR中,对于变量和常量的说法正确的是( )
A.2是常量,C,π,R是变量 B.2,π是常量,C,R是变量
C.2,C,π是常量,R是变量 D.2,π,R是常量,C是变量
4.已知6头大象1天的食品可供500只老鼠吃300天,假定每头大象的食量都一样,每只老鼠的食量也相等,那么t头大象1天的食品可供100只老鼠吃( )天.
A.250t B.300t C.500t D.600t
5.已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )
A.31 B.﹣31 C.41 D.﹣41
6.代数式的意义是( )
A.x除以y加3
B.y加3除x
C.y与3的和除以x
D.x除以y与3的和所得的商
7.点O,A,B,C在数轴上的位置如图所示,其中O为原点,BC=2,OA=OB,若C点所表示的数为x,则A点所表示的数为( )
A.﹣x+2 B.﹣x﹣2 C.x+2 D.﹣2
8.将正整数按如图所示的规律排列,若有序数对(n,m)表示第n排,从左到右第m个数,如(4,2)表示9,则表示123的有序数对是( )
A.(16,3) B.(15,3) C.(16,14) D.(15,13)
9.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.0.6元/千瓦时是自变量,y是因变量
C.y是自变量,x是因变量
D.x是自变量,y是因变量,0.6元/千瓦时是常量
10.下列各式:①1x;②2 3;③20%x;④a﹣b÷c;⑤;⑥x﹣5;其中,不符合代数式书写要求的有( )
A.5个 B.4个 C.3个 D.2个
二.填空题
11.下列各式:①1x;②2 3;③20%x;④a﹣b÷c;⑤;⑥x﹣5;其中,不符合代数式书写要求的有 (填写序号)
12.已知代数式m+2n=1,则代数式3m+6n+5的值为 .
13.如图,是一种数值转换机的运算程序.若输入的数为5,则第100次输出的数是 .
14.某超市的苹果价格如图,试说明代数式100﹣9.8x的实际意义 .
15.一个两位数,其十位数字是x,个位数字为y,则这个两位数可表示为: .
16.快餐每盒5元,买n盒需付m元,则其中常量是 .
17.观察下面的变化规律:=1﹣,=﹣,=,=,…根据上面的规律计算: +++…+= .
18.某种树木的分枝生长规律如图所示,则预计到第6年时,树木的分枝数为 ,其中自变量是 ,因变量是 .
年份 第一年 第二年 第三年 第四年 第五年
分枝数 1 1 2 3 5
19.举例说明代数式8a3的意义: .
20.某种水果的售价为每千克a元(a≤30),用面值为100元的人民币购买了3千克这种水果,应找回 元(用含a的代数式表示).
三.解答题
21.说出下列代数式的意义:
(1)2(a+3);
(2)a2+b2;
(3).
22.为鼓励居民节约用水,某市自来水公司实施阶梯水价:如果每月用水不超过8吨,按每吨2.3元收费;如果每月用水量超过8吨,则超出部分按每吨3.5元收费,设每月用水量为x吨.
(1)当每月用水量不超过8吨时,用含x的代数式表示用水费用为 元;
(2)当每月用水超过8吨时,需交水费多少元?(用含x的代数式表示)
(3)若小红家8月份用水12吨,则需交水费多少元?
23.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、b、c满足(c﹣5)2+|a+b|=0.
(1)a= ,b= ,c= .
(2)若将数轴折叠,使得A点与C点重合,则点B与表示数 的点重合;
(3)点A、B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= (用含t的代数式表示)
(4)请问:3BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
24.(1)根据生活经验,对代数式3x+2y作出解释.
(2)两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
25.小刚设计了一个如图所示的数值转换程序
(1)当输入x=2时,输出M的值为多少?
(2)当输入x=8时,输出M的值为多少?
(3)当输出M=10时,输入x的值为多少?
26.用字母表示图中阴影部分的面积.
27.某网店销售一种羽毛球拍和羽毛球,羽毛球拍每副定价150元,羽毛球每筒定价15元.“双11”期间,该网店决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一副球拍送两筒球;
方案二:球拍和球都打九折销售.
现某客户要在该网店购买球拍10副,球x筒(x>20).
(1)若该客户按方案一购买,需付款 元;(用含x的代数式表示)若该客户按方案二购买,需付款 元;(用含x的代数式表示)
(2)若x=40时,通过计算说明此时按哪种方案购买较为合算;
(3)当x=40时,你能给出一种更为省钱的购买方案吗?请直接写出你的购买方案.
参考答案与试题解析
一.选择题
1.解:A、C、D、是代数式,B是不等式,不是代数式.
故选:B.
2.解:根据题意得:
x+2y=2,
方程两边同时乘以﹣2得:﹣2x﹣4y=﹣4,
方程两边同时加上1得:1﹣2x﹣4y=1﹣4=﹣3,
故选:B.
3.解:在圆的周长计算公式C=2πR中,C和R是变量,2、π是常量,
故选:B.
4.解:∵6头大象1天的食品可供500只老鼠吃300天,
∴1头大象1天的食品可供500只老鼠吃50天,
∴t头大象1天的食品可供100只老鼠吃250t天.
故选:A.
5.解:∵x2﹣3x﹣12=0,
∴x2﹣3x=12.
原式=﹣3(x2﹣3x)+5=﹣3×12+5=﹣36+5=﹣31.
故选:B.
6.解:的意义是x除以y与3的和所得的商.
故选:D.
7.解:∵BC=2,C点所表示的数为x,
∴B点表示的数是x﹣2,
又∵OA=OB,
∴B点和A点表示的数互为相反数,
∴A点所表示的数是﹣(x﹣2),即﹣x+2.
故选:A.
8.解:由图可知,
第一排1个数,
第二排2个数,数字从大到小排列,
第三排3个数,数字从小到大排列,
第四排4个数,数字从大到小排列,
…,
则前n排的数字共有个数,
∵当n=15时,=120,
∴表示123的有序数对是(16,14),
故选:C.
9.解:在这个问题中,x是自变量,y是因变量,0.6元/千瓦时是常数.
故选:D.
10.解:①1x分数不能为带分数;
②2 3数与数相乘不能用“ ”;
③20%x,书写正确;
④a﹣b÷c不能出现除号;
⑤,书写正确;
⑥x﹣5,书写正确,
不符合代数式书写要求的有①②④共3个.
故选:C.
二.填空题
11.解:①1x分数不能为带分数;
②2 3数与数相乘不能用“ ”;
③20%x,书写正确;
④a﹣b÷c,书写错误;
⑤;书写正确;
⑥x﹣5,书写正确,
不符合代数式书写要求的有①②④共3个.
故答案为:①②④.
12.解:∵m+2n=1,
∴3m+6n+5=3(m+2n)+5=3×1+5=3+5=8.
故答案为:8.
13.解:当第1次输入的数为x=5时,
第一次输出5+3=8,
第二次输出8×=4,
第三次输出4×=2,
第四次输出2×=1,
第五次输出1+3=4,
除去前1次,以4,2,1循环,三个一循环,则第100次输出的数为1;
故答案为:1.
14.解:代数式100﹣9.8x的实际意义为:用100元买每斤9.8元的苹果x斤余下的钱.
故答案为:用100元买每斤9.8元的苹果x斤余下的钱.
15.解:根据两位数的表示方法得:
这个两位数表示为:10x+y.
故答案为:10x+y.
16.解:单价5元固定,是常量.
故答案为:5.
17.解:原式=1﹣+﹣+﹣+﹣+…+﹣
=1﹣
=.
故答案为:.
18.解:根据所给的具体数据发现:
从第三个数据开始,每一个数据是前面两个数据的和,则第6年的时候是3+5=8个.
自变量是年份,因变量是分枝数,
故答案为:8,年份,分枝数.
19.解:如一个正方体的棱长是a,一个正方体的体积是a3,那么8个正方体的体积是8a3.
故答案为:如一个正方体的棱长是a,一个正方体的体积是a3,那么8个正方体的体积是8a3.
20.解:∵购买这种售价是每千克a元的水果3千克需3a元,
∴根据题意,应找回(100﹣3a)元.
故答案为:(100﹣3a).
三.解答题
21.解:(1)2(a+3)的意义是2与(a+3)的积;
(2)a2+b2的意义是a,b的平方的和;
(3)的意义是(n+1)除以(n﹣1)的商.
22.解:(1)当x不超过8吨时,这个月的水费为:2.3x;
故答案为:2.3x.
(2)当x超过8吨时,
这个月的水费为:8×2.3+(x﹣8)×3.5=18.4+3.5x﹣28=3.5x﹣9.6,
∴需交水费(3.5x﹣9.6)元.
(3)当x=12时,
3.5×12﹣9.6=42﹣9.6=32.4(元)
∴用水12吨需交水费32.4元.
23.解:(1)∵(c﹣5)2+|a+b|=0,
∴a+b=0,c﹣5=0,
解得a=﹣b,c=5,
∵b是最小的正整数,
∴b=1;a=﹣1
故答案为:﹣1,1,5;
(2)点A与点C的中点对应的数为:=2,
点B到2的距离为1,所以与点B重合的数是:2+1=3.
故答案为:3;
(3)AB=t+2t+2=3t+2,AC=t+3t+6=4t+6,BC=t+4;
故答案为:3t+2,4t+6,t+4.
(4)∵3BC﹣AB=3(t+4)﹣(3t+2)=10,
∴3BC﹣AB的值不随着时间t的变化而改变,其值为10.
24.解:(1)根据生活经验,对代数式3x+2y作出解释.
某水果超市推出两款促销水果,其中苹果每斤x元,香蕉每斤y元,小明买了3斤苹果和2斤香蕉,共花去(3x+2y)元钱.
(2)两个有理数的和是负数,那么这两个数一定都是负数,这种说法对吗?如果不对,请举例说明?
这种说法不正确,例如:﹣4+3=﹣1.
25.解:(1)当x=2时,M==;
(2)当x=8时,M=+1=5;
(3)若+1=10,则x=18或x=﹣18(舍);
若=10,则x=19(舍)或x=﹣21;
综上,当输出M=10时,输入x的值为18或﹣21.
26.解:(1)阴影部分的面积=ab﹣bx;
(2)阴影部分的面积=R2﹣πR2.
27.解:(1)根据题意,得
方案一:1500+15(x﹣20)=15x+1200
方案二:(150×10+15x)×90%=13.5x+1350
故答案为15x+1200;13.5x+1350.
(2)当x=40时,
方案一:15x+1200=15×40+1200=1800(元)
方案二:13.5x+1350=13.5×40+1350=1890(元)
∵1890>1800
∴按方案一购买较合算.
(3)先按方案一购买10副球拍获赠20筒球,再按方案二购买20筒球
则需付款1500+20×15×90%=1770(元),
比方案一和方案二都省钱.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
