2021-2022学年人教版九年级数学下册27.1图形的相似 同步达标测评(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册27.1图形的相似 同步达标测评(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 11:13:56 | ||
图片预览


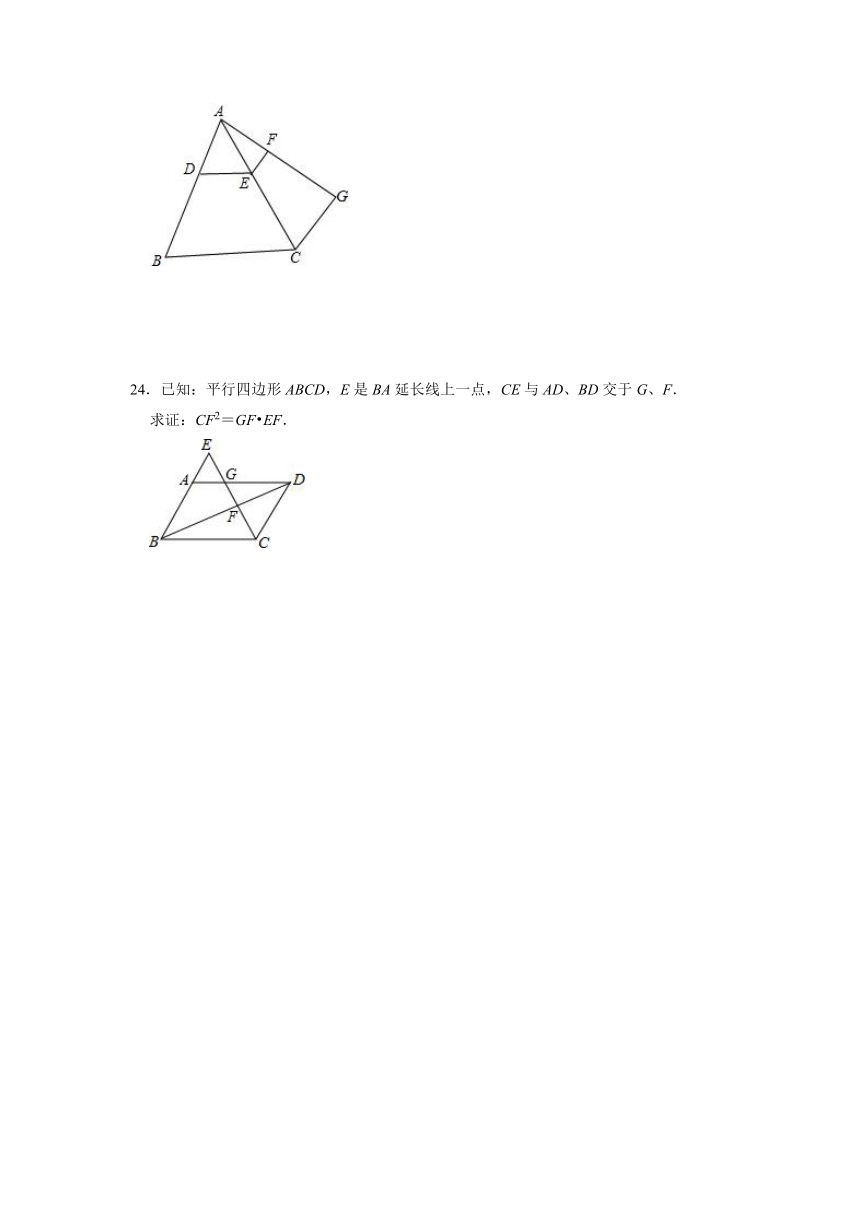
文档简介
2021-2022学年人教版九年级数学下册《27.1图形的相似》
同步达标测评(附答案)
一.选择题(共12小题,满分48分)
1.若=,则的值为( )
A.1 B. C. D.
2.已知,则的值是( )
A. B. C. D.
3.已知2x=3y(y≠0),则下面结论成立的是( )
A.= B.= C.= D.=
4.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
5.已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长( )
A.18cm B.5cm C.6cm D.±6cm
6.在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是( )
A.1250km B.125km C.12.5km D.1.25km
7.已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )
A.AB2=AC2+BC2 B.BC2=AC BA
C. D.
8.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
9.如图所示,△ABC中若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
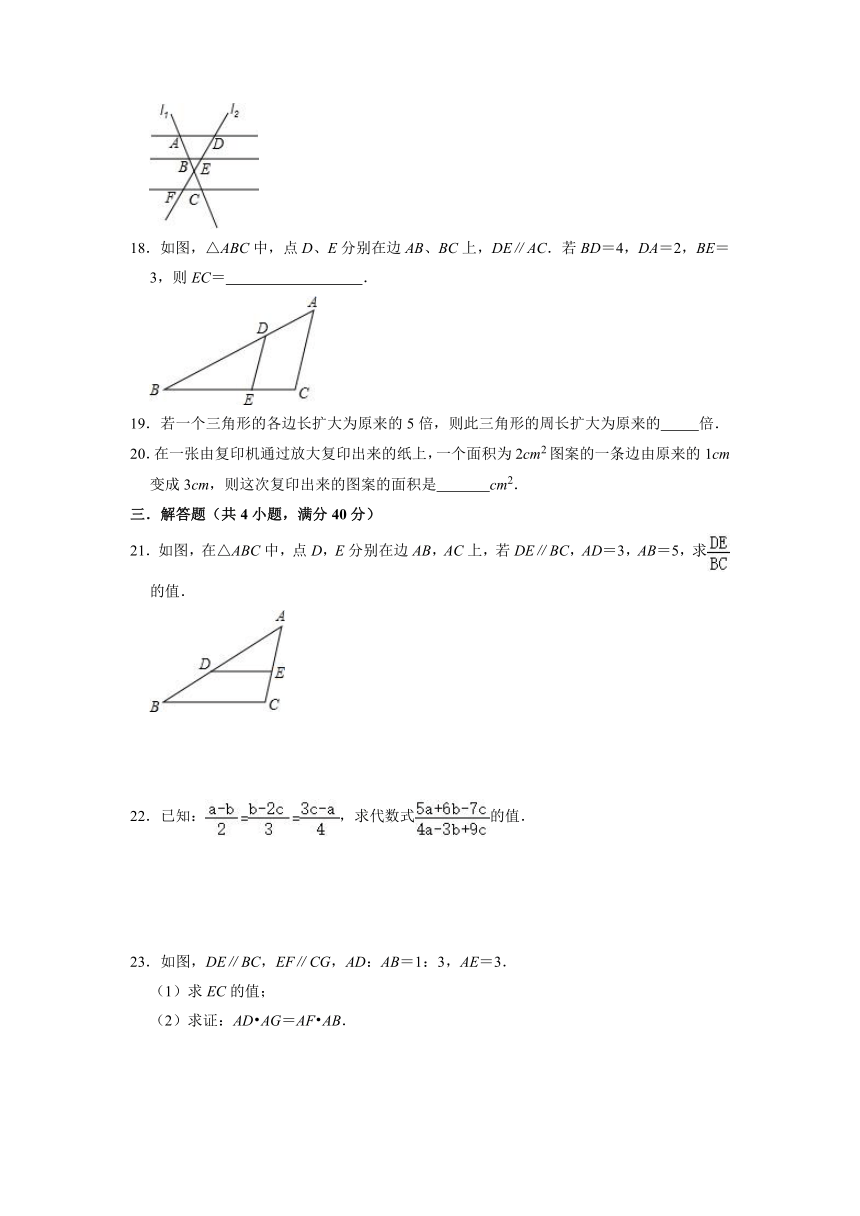
10.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A. B. C. D.
11.下列图形一定是相似图形的是( )
A.两个矩形 B.两个正方形
C.两个直角三角形 D.两个等腰三角形
12.用一个2倍放大镜照一个△ABC,下面说法中错误的是( )
A.△ABC放大后,面积是原来的2倍
B.△ABC放大后,各边长是原来的2倍
C.△ABC放大后,周长是原来的2倍
D.△ABC放大后,面积是原来的4倍
二.填空题(共8小题,满分32分)
13.已知=,则的值为 .
14.若a:b:c=1:3:2,且a+b+c=24,则a+b﹣c= .
15.已知线段a=2cm,b=8cm,那么线段a和b的比例中项为 cm.
16.已知三个数:1,2,,请你添上一个数,使它们能构成一个比例式,则这个数是 (只填一个).
17.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,=,DE=6,则EF= .
18.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
19.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
20.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是 cm2.
三.解答题(共4小题,满分40分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求的值.
22.已知:,求代数式的值.
23.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
24.已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.
求证:CF2=GF EF.
参考答案
一.选择题(共12小题,满分48分)
1.解:∵=,
∴==.
故选:D.
2.解:由,得
a=b,
==﹣,
故选:D.
3.解:A、因为2x=3y,两边都除以2y,得=,故A符合题意;
B、两边除以不同的整式,故B不符合题意;
C、因为2x=3y,两边都除以2y,得=,故C不符合题意;
D、两边除以不同的整式,故D不符合题意;
故选:A.
4.解:根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
所给选项中,只有D符合,3×18=6×9,故选:D.
5.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=4×9,解得c=±6(线段是正数,负值舍去),
故选:C.
6.解:设甲、乙两地间的实际距离为x,则:
=,
解得x=125000cm=1.25km.
故选:D.
7.解:根据黄金分割的定义可知:.
故选:C.
8.解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
9.解:∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DE=BF,BD=EF;
∵DE∥BC,
∴==,
==,
∵EF∥AB,
∴=,=,
∴,
故选:C.
10.解:∵l1∥l2∥l3,,
∴===,
故选:D.
11.解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意;
B、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题意;
C、两个直角三角形,只有一个直角相同,锐角不一定相等,故不符合题意;
D、两个等腰三角形顶角不一定相等,故不符合题意.
故选:B.
12.解:∵放大前后的三角形相似,
∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍.
故选:A.
二.填空题(共8小题,满分32分)
13.解:∵=,
∴设x=k,y=3k,
∴==﹣,
故答案为:﹣.
14.解:∵a:b:c=1:3:2,
∴设a=k,则b=3k,c=2k,
又∵a+b+c=24,
∴k+3k+2k=24,
∴k=4,
∴a+b﹣c=k+3k﹣2k=2k=2×4=8.
故答案是:8.
15.解:根据比例中项的概念结合比例的基本性质,
得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则x2=2×8,x=±4(线段是正数,负值舍去).
故答案为4.
16.解:根据比例式的概念,可得:
1×÷2=;
2×÷1=2
或1×2÷=等.
答案不唯一.
17.解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
18.解:∵DE∥AC,
∴,
即,
解得:EC=.
故答案为:.
19.解:∵一个三角形的各边长扩大为原来的5倍,
∴扩大后的三角形与原三角形相似,
∵相似三角形的周长的比等于相似比,
∴这个三角形的周长扩大为原来的5倍,
故答案为:5.
20.解:∵在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,
∴相似比=1:3,
∴面积比=(1:3)2=1:9,
∴这次复印出来的图案的面积=2×9=18(cm2).
故答案为18.
三.解答题(共4小题,满分40分)
21.解:∵DE∥BC,
∴=,
∵AD=3,AB=5,
∴=.
22.解:设=t,
∴,
解得,,
∴==.
23.(1)解:
∵DE∥BC,
∴=,
又=,AE=3,
∴=,
解得AC=9,
∴EC=AC﹣AE=9﹣3=6;
(2)证明:
∵DE∥BC,EF∥CG,
∴==,
∴AD AG=AF AB.
24.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴=,=,
∴=,
即CF2=GF EF.
同步达标测评(附答案)
一.选择题(共12小题,满分48分)
1.若=,则的值为( )
A.1 B. C. D.
2.已知,则的值是( )
A. B. C. D.
3.已知2x=3y(y≠0),则下面结论成立的是( )
A.= B.= C.= D.=
4.下列线段中,能成比例的是( )
A.3cm、6cm、8cm、9cm B.3cm、5cm、6cm、9cm
C.3cm、6cm、7cm、9cm D.3cm、6cm、9cm、18cm
5.已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长( )
A.18cm B.5cm C.6cm D.±6cm
6.在比例尺为1:5000的地图上,量得甲、乙两地的距离为25cm,则甲、乙两地间的实际距离是( )
A.1250km B.125km C.12.5km D.1.25km
7.已知如图,点C是线段AB的黄金分割点(AC>BC),则下列结论中正确的是( )
A.AB2=AC2+BC2 B.BC2=AC BA
C. D.
8.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )
A.1 B.2 C.3 D.4
9.如图所示,△ABC中若DE∥BC,EF∥AB,则下列比例式正确的是( )
A. B. C. D.
10.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为( )
A. B. C. D.
11.下列图形一定是相似图形的是( )
A.两个矩形 B.两个正方形
C.两个直角三角形 D.两个等腰三角形
12.用一个2倍放大镜照一个△ABC,下面说法中错误的是( )
A.△ABC放大后,面积是原来的2倍
B.△ABC放大后,各边长是原来的2倍
C.△ABC放大后,周长是原来的2倍
D.△ABC放大后,面积是原来的4倍
二.填空题(共8小题,满分32分)
13.已知=,则的值为 .
14.若a:b:c=1:3:2,且a+b+c=24,则a+b﹣c= .
15.已知线段a=2cm,b=8cm,那么线段a和b的比例中项为 cm.
16.已知三个数:1,2,,请你添上一个数,使它们能构成一个比例式,则这个数是 (只填一个).
17.如图,AD∥BE∥CF,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F,=,DE=6,则EF= .
18.如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
19.若一个三角形的各边长扩大为原来的5倍,则此三角形的周长扩大为原来的 倍.
20.在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是 cm2.
三.解答题(共4小题,满分40分)
21.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,AD=3,AB=5,求的值.
22.已知:,求代数式的值.
23.如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
(1)求EC的值;
(2)求证:AD AG=AF AB.
24.已知:平行四边形ABCD,E是BA延长线上一点,CE与AD、BD交于G、F.
求证:CF2=GF EF.
参考答案
一.选择题(共12小题,满分48分)
1.解:∵=,
∴==.
故选:D.
2.解:由,得
a=b,
==﹣,
故选:D.
3.解:A、因为2x=3y,两边都除以2y,得=,故A符合题意;
B、两边除以不同的整式,故B不符合题意;
C、因为2x=3y,两边都除以2y,得=,故C不符合题意;
D、两边除以不同的整式,故D不符合题意;
故选:A.
4.解:根据如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
所给选项中,只有D符合,3×18=6×9,故选:D.
5.解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.
所以c2=4×9,解得c=±6(线段是正数,负值舍去),
故选:C.
6.解:设甲、乙两地间的实际距离为x,则:
=,
解得x=125000cm=1.25km.
故选:D.
7.解:根据黄金分割的定义可知:.
故选:C.
8.解:∵DE∥BC,
∴,
即,
解得:EC=2,
故选:B.
9.解:∵DE∥BC,EF∥AB,
∴四边形DEFB是平行四边形,
∴DE=BF,BD=EF;
∵DE∥BC,
∴==,
==,
∵EF∥AB,
∴=,=,
∴,
故选:C.
10.解:∵l1∥l2∥l3,,
∴===,
故选:D.
11.解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意;
B、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题意;
C、两个直角三角形,只有一个直角相同,锐角不一定相等,故不符合题意;
D、两个等腰三角形顶角不一定相等,故不符合题意.
故选:B.
12.解:∵放大前后的三角形相似,
∴放大后三角形的内角度数不变,面积为原来的4倍,周长和边长均为原来的2倍.
故选:A.
二.填空题(共8小题,满分32分)
13.解:∵=,
∴设x=k,y=3k,
∴==﹣,
故答案为:﹣.
14.解:∵a:b:c=1:3:2,
∴设a=k,则b=3k,c=2k,
又∵a+b+c=24,
∴k+3k+2k=24,
∴k=4,
∴a+b﹣c=k+3k﹣2k=2k=2×4=8.
故答案是:8.
15.解:根据比例中项的概念结合比例的基本性质,
得:比例中项的平方等于两条线段的乘积.
设它们的比例中项是x,则x2=2×8,x=±4(线段是正数,负值舍去).
故答案为4.
16.解:根据比例式的概念,可得:
1×÷2=;
2×÷1=2
或1×2÷=等.
答案不唯一.
17.解:∵AD∥BE∥CF,
∴=,即=,
∴EF=9.
故答案为9.
18.解:∵DE∥AC,
∴,
即,
解得:EC=.
故答案为:.
19.解:∵一个三角形的各边长扩大为原来的5倍,
∴扩大后的三角形与原三角形相似,
∵相似三角形的周长的比等于相似比,
∴这个三角形的周长扩大为原来的5倍,
故答案为:5.
20.解:∵在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,
∴相似比=1:3,
∴面积比=(1:3)2=1:9,
∴这次复印出来的图案的面积=2×9=18(cm2).
故答案为18.
三.解答题(共4小题,满分40分)
21.解:∵DE∥BC,
∴=,
∵AD=3,AB=5,
∴=.
22.解:设=t,
∴,
解得,,
∴==.
23.(1)解:
∵DE∥BC,
∴=,
又=,AE=3,
∴=,
解得AC=9,
∴EC=AC﹣AE=9﹣3=6;
(2)证明:
∵DE∥BC,EF∥CG,
∴==,
∴AD AG=AF AB.
24.证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴=,=,
∴=,
即CF2=GF EF.
