2021-2022学年苏科版八年级数学上册 第5章平面直角坐标系 单元综合测评(Word版 含解析)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册 第5章平面直角坐标系 单元综合测评(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 147.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 11:15:57 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学上册《第5章平面直角坐标系》单元综合测评(附答案)
一.选择题(共8小题,满分40分)
1.已知点P(0,m)在y轴的负半轴上,则点M(﹣m,﹣m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知点A(m2﹣2,5m+4)在第一象限的角平分线上,则m的值为( )
A.6 B.﹣1 C.﹣1或6 D.2或3
3.下列说法中正确的有( )个.
①(﹣1,﹣x2)位于第三象限;②的平方根是3;③若x+y=0,则点P(x,y)在第二、四象限角平分线上;④点A(2,a)和点B(b,﹣3)关于x轴对称,则a+b的值为5;⑤点N(1,n)到x轴的距离为n.
A.1 B.2 C.3 D.4
4.在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(1,3)或(﹣9,3) D.(﹣4,8)或(﹣4,﹣2)
5.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3) B.(3,2) C.(0,3) D.(1,3)
6.点P(1﹣m,m)不可能在第( )象限.
A.一 B.二 C.三 D.四
7.如图,A,B两点的坐标分别为(4,0),(0,2),将线段AB平移到线段A1B1的位置.若A1,B1两点的坐标分别为(b,2),(2,a),则a+b的值为( )
A.4 B.6 C.8 D.10
8.在平面直角坐标系中,把点P(2,3)绕原点旋转90°得到点P1,则点P1的坐标是( )
A.(﹣3,2) B.(﹣2,3)
C.(﹣2,3)或(2,﹣3) D.(﹣3,2)或(3,﹣2)
二.填空题(共8小题,满分40分)
9.已知点A(m,﹣5),B(3,m+1),且直线AB∥x轴,则m的值是 .
10.在平面直角坐标系中,点M在第四象限,且点M到y轴的距离是3,到x轴的距离是1,则点M的坐标是 .
11.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是 .
12.若将教室里第5行、第3列的座位表示为(5,3),则第4行、第6列的座位表示为 .
13.已知点P(a,2a+3)点在第二、四象限的角平分线上,则a= .
14.如图,在平面直角坐标系中,点A和B的坐标分别为(2,0),(0,﹣4),若将线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为 .
15.点A(5,﹣2)关于x轴对称的点的坐标为 .
16.如图第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
三.解答题(共5小题,满分40分)
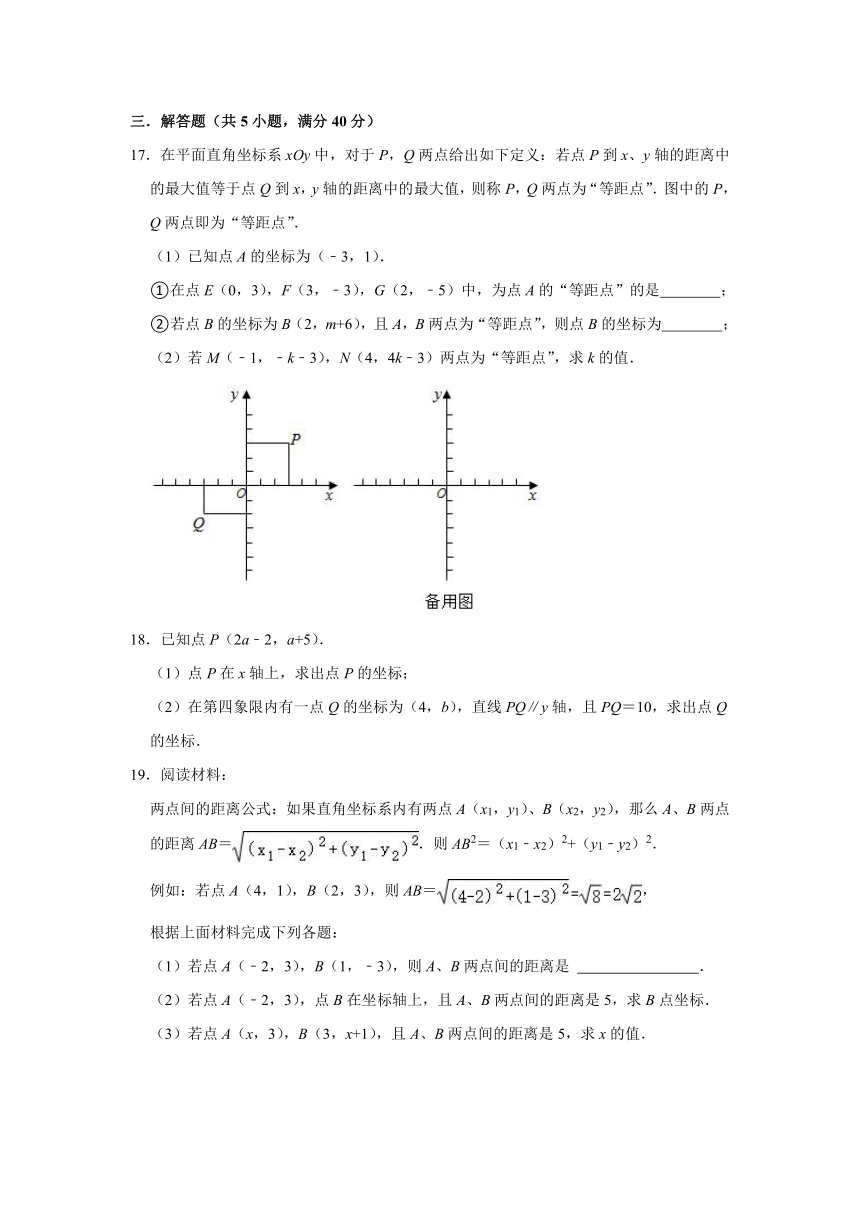
17.在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”.图中的P,Q两点即为“等距点”.
(1)已知点A的坐标为(﹣3,1).
①在点E(0,3),F(3,﹣3),G(2,﹣5)中,为点A的“等距点”的是 ;
②若点B的坐标为B(2,m+6),且A,B两点为“等距点”,则点B的坐标为 ;
(2)若M(﹣1,﹣k﹣3),N(4,4k﹣3)两点为“等距点”,求k的值.
18.已知点P(2a﹣2,a+5).
(1)点P在x轴上,求出点P的坐标;
(2)在第四象限内有一点Q的坐标为(4,b),直线PQ∥y轴,且PQ=10,求出点Q的坐标.
19.阅读材料:
两点间的距离公式:如果直角坐标系内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离AB=.则AB2=(x1﹣x2)2+(y1﹣y2)2.
例如:若点A(4,1),B(2,3),则AB=,
根据上面材料完成下列各题:
(1)若点A(﹣2,3),B(1,﹣3),则A、B两点间的距离是 .
(2)若点A(﹣2,3),点B在坐标轴上,且A、B两点间的距离是5,求B点坐标.
(3)若点A(x,3),B(3,x+1),且A、B两点间的距离是5,求x的值.
20.已知点A(a,﹣5),B(8,b) 根据下列要求确定a,b的值
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB∥y轴
(4)A,B两点在第二、第四象限的角平分线上.
21.已知点P(3m﹣6,m+1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大5;
(4)点P在过点A(﹣1,2),且与x轴平行的直线上.
参考答案
一.选择题(共8小题,满分40分)
1.解:由点P(0,m)在y轴的负半轴上,得
m<0.
由不等式的性质,得
﹣m>0,﹣m+1>1,
则点M(﹣m,﹣m+1)在第一象限,
故选:A.
2.解:∵点A(m2﹣2,5m+4)在第一象限的角平分线上,
∴m2﹣2=5m+4,
∴m2﹣5m﹣6=0,
解得m1=﹣1,m2=6,
当m=﹣1时,m2﹣2=﹣1,
点A(﹣1,﹣1)在第三象限,不符合题意,
所以m的值为6.
故选:A.
3.解:当x=0时,(﹣1,﹣x2)位于x轴上,故①说法错误;
的平方根是±3,故②说法错误;
若x+y=0,则点P(x,y)在第二、四象限角平分线上,故③说法正确;
∵点A(2,a)与点B(b,﹣3)关于x轴对称,
∴a=3,b=2,
∴a+b的值是:3+2=5.故④说法正确;
⑤点N(1,n)到x轴的距离为|n|.故⑤说法错误;
说法中正确的有③④,共2个.
故选:B.
4.解:∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8).
故选:D.
5.解:如图所示:棋子“炮”的点的坐标为:(1,3).
故选:D.
6.解:当m<0时,1﹣m>0,此时点P在第四象限,故选项D不合题意;
当0<m<1时,1﹣m>0,此时点P在第一象限,故选项A不合题意;
当m>1时,1﹣m<0,此时点P在第二象限,故选项B不合题意;
当m=0时,点P在x轴上;当m=1时,点P在y轴上;
∴点P(1﹣m,m)不可能在第三象限.
故选:C.
7.解:由题意,线段AB,向右平移2个单位,再向上平移2个单位得到A1B1,
∴a=4,b=6,
∴a+b=10,
故选:D.
8.解:如图,满足条件的点P1的坐标为(﹣3,2)或(3,﹣2),
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵点A(m,﹣5),B(3,m+1),直线AB∥x轴,
∴m+1=﹣5,
解得m=﹣6.
故答案为:﹣6.
10.解:∵点P在第四象限,且点M到y轴的距离是3,到x轴的距离是1,
∴点P的横坐标是3,纵坐标是﹣1,即点P的坐标为(3,﹣1).
故答案为:(3,﹣1).
11.解:将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是(2﹣1,6+2),
即(1,8).
故答案是:(1,8).
12.解:将教室里第5行、第3列的座位表示为(5,3),则第4行、第6列的座位表示为(4,6);
故答案为:(4,6).
13.解:由点P(a,2a+3)点在第二、四象限的角平分线上,得
a+2a+3=0,
解得a=﹣1,
故答案为:﹣1.
14.解:如图,过点C作CH⊥x轴于H.
∵A(2,0),B(0,4),
∴OA=2,OB=4,
∵∠AHC=∠AOB=∠BCA=90°,
∴∠CAH+∠BAO=90°,∠ABO+∠BAO=90°,
∴∠CAH=∠ABO,
在△AOB和△CHA中,
,
∴△AOB≌△CHA(AAS),
∴CH=OA=2,AH=OB=4,
∴OH=AH﹣OA=2,
∴C(﹣2,2).
故答案为:(﹣2,2).
15.解:∵点A(5,﹣2),
∴点A关于x轴对称的点的坐标为 (5,2).
故答案为:(5,2).
16.解:设平移后点P、Q的对应点分别是P′、Q′.
分两种情况:
①P′在y轴上,Q′在x轴上,
则P′横坐标为0,Q′纵坐标为0,
∵0﹣(n﹣3)=﹣n+3,
∴n﹣n+3=3,
∴点P平移后的对应点的坐标是(0,3);
②P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∵0﹣m=﹣m,
∴m﹣4﹣m=﹣4,
∴点P平移后的对应点的坐标是(﹣4,0);
综上可知,点P平移后的对应点的坐标是(0,3)或(﹣4,0).
故答案为:(0,3)或(﹣4,0).
三.解答题(共5小题,满分40分)
17.解:(1)①∵点A的坐标为(﹣3,1),
∴点A到x、y轴的距离中的最大值等于3,
∵点E到x、y轴的距离中的最大值等于3,
点F到x、y轴的距离中的最大值等于3,
点G到x、y轴的距离中的最大值等于5,
∴为点A的“等距点”的是E,F,
故答案为:E,F;
②∵A,B两点为“等距点”,
∴|m+6|=3,
∴m+6=±3,
∴点B的坐标为(2,3)或(2,﹣3),
故答案为:(2,3)或(2,﹣3);
(2)∵N(4,4k﹣3)到x轴的距离为|4k﹣3|,到y轴的距离为4,
若|4k﹣3|≤4,即,
则有|﹣k﹣3|=4,
解得k=﹣7或k=1,
∵k=﹣7不合题意,舍去,
∴k=1,
若|4k﹣3|>4,即或,
则|﹣k﹣3|=|4k﹣3|,
解得:k=0,或k=2,
∵k=0不合题意,舍去,
∴k=2,
综上,k的值为1或2.
18.解:(1)因为p在x轴上,
所以a+5=0,
所以a=﹣5.
∴2a﹣2=﹣12,
所以P(﹣12,0);
(2)因为直线PQ||y轴,
所以2a﹣2=4,
所以a=3.
所以a+5=8.
所以P(4,8),
∵点Q在第四象限,且PQ=10,
∴b=8﹣10=﹣2,
∴Q(4,﹣2).
19.解:(1)∵点A(﹣2,3),B(1,﹣3),
∴AB==3;
故答案为3;
(2)当B点在x轴上,设B(t,0),
而点A(﹣2,3),A、B两点间的距离是5,
∴(﹣2﹣t)2+(0﹣3)2=52,解得t=2或﹣6,
此时B点坐标为(2,0)或(﹣6,0);
当B点在y轴上,设B(0,m),
而点A(﹣2,3),A、B两点间的距离是5,
∴(0+2)2+(m﹣3)2=52,解得m=3+或3﹣,
此时B点坐标为(0,3+)或(0,3﹣);
综上所述,B点坐标为(2,0)或(﹣6,0)或(0,3+)或(0,3﹣);
(3)∵点A(x,3),B(3,x+1),且A、B两点间的距离是5,
∴(x﹣3)2+(3﹣x﹣1)2=52,
整理得x2﹣5x﹣6=0,
解得x1=﹣1,x2=6,
即x的值为﹣1或6.
20.解:(1)∵点A(a,﹣5),B(8,b)关于y轴对称,
∴a=﹣8,b=﹣5;
(2))∵点A(a,﹣5),B(8,b)关于x轴对称,
∴a=8,b=5;
(3)∵AB∥y轴,
∴a=8,b为不等于﹣5的实数;
(4)∵A,B两点在第二、第四象限的角平分线上,
∴a=5,b=﹣8.
21.解:(1)∵点P(3m﹣6,m+1)在y轴上,
∴3m﹣6=0,
解得m=2,
∴m+1=2+1=3,
∴点P的坐标为(0,3);
(2)点P(3m﹣6,m+1)在x轴上,
∴m+1=0,
解得m=﹣1,
∴3m﹣6=3×(﹣1)﹣6=﹣9,
∴点P的坐标为(﹣9,0);
(3)∵点P(3m﹣6,m+1)的纵坐标比横坐标大5,
∴m+1﹣(3m﹣6)=5,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
m+1=1+1=2,
∴点P的坐标为(﹣3,2);
(4)∵点P(3m﹣6,m+1)在过点A(﹣1,2)且与x轴平行的直线上,
∴m+1=2,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
m+1=1+1=2,
∴点P的坐标为(﹣3,2).
一.选择题(共8小题,满分40分)
1.已知点P(0,m)在y轴的负半轴上,则点M(﹣m,﹣m+1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知点A(m2﹣2,5m+4)在第一象限的角平分线上,则m的值为( )
A.6 B.﹣1 C.﹣1或6 D.2或3
3.下列说法中正确的有( )个.
①(﹣1,﹣x2)位于第三象限;②的平方根是3;③若x+y=0,则点P(x,y)在第二、四象限角平分线上;④点A(2,a)和点B(b,﹣3)关于x轴对称,则a+b的值为5;⑤点N(1,n)到x轴的距离为n.
A.1 B.2 C.3 D.4
4.在平面直角坐标系中,点A的坐标为(﹣4,3),AB∥y轴,AB=5,则点B的坐标为( )
A.(1,3) B.(﹣4,8)
C.(1,3)或(﹣9,3) D.(﹣4,8)或(﹣4,﹣2)
5.象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(﹣3,3) B.(3,2) C.(0,3) D.(1,3)
6.点P(1﹣m,m)不可能在第( )象限.
A.一 B.二 C.三 D.四
7.如图,A,B两点的坐标分别为(4,0),(0,2),将线段AB平移到线段A1B1的位置.若A1,B1两点的坐标分别为(b,2),(2,a),则a+b的值为( )
A.4 B.6 C.8 D.10
8.在平面直角坐标系中,把点P(2,3)绕原点旋转90°得到点P1,则点P1的坐标是( )
A.(﹣3,2) B.(﹣2,3)
C.(﹣2,3)或(2,﹣3) D.(﹣3,2)或(3,﹣2)
二.填空题(共8小题,满分40分)
9.已知点A(m,﹣5),B(3,m+1),且直线AB∥x轴,则m的值是 .
10.在平面直角坐标系中,点M在第四象限,且点M到y轴的距离是3,到x轴的距离是1,则点M的坐标是 .
11.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是 .
12.若将教室里第5行、第3列的座位表示为(5,3),则第4行、第6列的座位表示为 .
13.已知点P(a,2a+3)点在第二、四象限的角平分线上,则a= .
14.如图,在平面直角坐标系中,点A和B的坐标分别为(2,0),(0,﹣4),若将线段AB绕点A顺时针旋转90°得到线段AC,则点C的坐标为 .
15.点A(5,﹣2)关于x轴对称的点的坐标为 .
16.如图第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
三.解答题(共5小题,满分40分)
17.在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x、y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”.图中的P,Q两点即为“等距点”.
(1)已知点A的坐标为(﹣3,1).
①在点E(0,3),F(3,﹣3),G(2,﹣5)中,为点A的“等距点”的是 ;
②若点B的坐标为B(2,m+6),且A,B两点为“等距点”,则点B的坐标为 ;
(2)若M(﹣1,﹣k﹣3),N(4,4k﹣3)两点为“等距点”,求k的值.
18.已知点P(2a﹣2,a+5).
(1)点P在x轴上,求出点P的坐标;
(2)在第四象限内有一点Q的坐标为(4,b),直线PQ∥y轴,且PQ=10,求出点Q的坐标.
19.阅读材料:
两点间的距离公式:如果直角坐标系内有两点A(x1,y1)、B(x2,y2),那么A、B两点的距离AB=.则AB2=(x1﹣x2)2+(y1﹣y2)2.
例如:若点A(4,1),B(2,3),则AB=,
根据上面材料完成下列各题:
(1)若点A(﹣2,3),B(1,﹣3),则A、B两点间的距离是 .
(2)若点A(﹣2,3),点B在坐标轴上,且A、B两点间的距离是5,求B点坐标.
(3)若点A(x,3),B(3,x+1),且A、B两点间的距离是5,求x的值.
20.已知点A(a,﹣5),B(8,b) 根据下列要求确定a,b的值
(1)A,B两点关于y轴对称;
(2)A,B两点关于x轴对称;
(3)AB∥y轴
(4)A,B两点在第二、第四象限的角平分线上.
21.已知点P(3m﹣6,m+1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P在x轴上;
(3)点P的纵坐标比横坐标大5;
(4)点P在过点A(﹣1,2),且与x轴平行的直线上.
参考答案
一.选择题(共8小题,满分40分)
1.解:由点P(0,m)在y轴的负半轴上,得
m<0.
由不等式的性质,得
﹣m>0,﹣m+1>1,
则点M(﹣m,﹣m+1)在第一象限,
故选:A.
2.解:∵点A(m2﹣2,5m+4)在第一象限的角平分线上,
∴m2﹣2=5m+4,
∴m2﹣5m﹣6=0,
解得m1=﹣1,m2=6,
当m=﹣1时,m2﹣2=﹣1,
点A(﹣1,﹣1)在第三象限,不符合题意,
所以m的值为6.
故选:A.
3.解:当x=0时,(﹣1,﹣x2)位于x轴上,故①说法错误;
的平方根是±3,故②说法错误;
若x+y=0,则点P(x,y)在第二、四象限角平分线上,故③说法正确;
∵点A(2,a)与点B(b,﹣3)关于x轴对称,
∴a=3,b=2,
∴a+b的值是:3+2=5.故④说法正确;
⑤点N(1,n)到x轴的距离为|n|.故⑤说法错误;
说法中正确的有③④,共2个.
故选:B.
4.解:∵AB∥y轴,
∴A、B两点的横坐标相同,
又AB=5,
∴B点纵坐标为:3+5=8或3﹣5=﹣2,
∴B点的坐标为:(﹣4,﹣2)或(﹣4,8).
故选:D.
5.解:如图所示:棋子“炮”的点的坐标为:(1,3).
故选:D.
6.解:当m<0时,1﹣m>0,此时点P在第四象限,故选项D不合题意;
当0<m<1时,1﹣m>0,此时点P在第一象限,故选项A不合题意;
当m>1时,1﹣m<0,此时点P在第二象限,故选项B不合题意;
当m=0时,点P在x轴上;当m=1时,点P在y轴上;
∴点P(1﹣m,m)不可能在第三象限.
故选:C.
7.解:由题意,线段AB,向右平移2个单位,再向上平移2个单位得到A1B1,
∴a=4,b=6,
∴a+b=10,
故选:D.
8.解:如图,满足条件的点P1的坐标为(﹣3,2)或(3,﹣2),
故选:D.
二.填空题(共8小题,满分40分)
9.解:∵点A(m,﹣5),B(3,m+1),直线AB∥x轴,
∴m+1=﹣5,
解得m=﹣6.
故答案为:﹣6.
10.解:∵点P在第四象限,且点M到y轴的距离是3,到x轴的距离是1,
∴点P的横坐标是3,纵坐标是﹣1,即点P的坐标为(3,﹣1).
故答案为:(3,﹣1).
11.解:将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是(2﹣1,6+2),
即(1,8).
故答案是:(1,8).
12.解:将教室里第5行、第3列的座位表示为(5,3),则第4行、第6列的座位表示为(4,6);
故答案为:(4,6).
13.解:由点P(a,2a+3)点在第二、四象限的角平分线上,得
a+2a+3=0,
解得a=﹣1,
故答案为:﹣1.
14.解:如图,过点C作CH⊥x轴于H.
∵A(2,0),B(0,4),
∴OA=2,OB=4,
∵∠AHC=∠AOB=∠BCA=90°,
∴∠CAH+∠BAO=90°,∠ABO+∠BAO=90°,
∴∠CAH=∠ABO,
在△AOB和△CHA中,
,
∴△AOB≌△CHA(AAS),
∴CH=OA=2,AH=OB=4,
∴OH=AH﹣OA=2,
∴C(﹣2,2).
故答案为:(﹣2,2).
15.解:∵点A(5,﹣2),
∴点A关于x轴对称的点的坐标为 (5,2).
故答案为:(5,2).
16.解:设平移后点P、Q的对应点分别是P′、Q′.
分两种情况:
①P′在y轴上,Q′在x轴上,
则P′横坐标为0,Q′纵坐标为0,
∵0﹣(n﹣3)=﹣n+3,
∴n﹣n+3=3,
∴点P平移后的对应点的坐标是(0,3);
②P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∵0﹣m=﹣m,
∴m﹣4﹣m=﹣4,
∴点P平移后的对应点的坐标是(﹣4,0);
综上可知,点P平移后的对应点的坐标是(0,3)或(﹣4,0).
故答案为:(0,3)或(﹣4,0).
三.解答题(共5小题,满分40分)
17.解:(1)①∵点A的坐标为(﹣3,1),
∴点A到x、y轴的距离中的最大值等于3,
∵点E到x、y轴的距离中的最大值等于3,
点F到x、y轴的距离中的最大值等于3,
点G到x、y轴的距离中的最大值等于5,
∴为点A的“等距点”的是E,F,
故答案为:E,F;
②∵A,B两点为“等距点”,
∴|m+6|=3,
∴m+6=±3,
∴点B的坐标为(2,3)或(2,﹣3),
故答案为:(2,3)或(2,﹣3);
(2)∵N(4,4k﹣3)到x轴的距离为|4k﹣3|,到y轴的距离为4,
若|4k﹣3|≤4,即,
则有|﹣k﹣3|=4,
解得k=﹣7或k=1,
∵k=﹣7不合题意,舍去,
∴k=1,
若|4k﹣3|>4,即或,
则|﹣k﹣3|=|4k﹣3|,
解得:k=0,或k=2,
∵k=0不合题意,舍去,
∴k=2,
综上,k的值为1或2.
18.解:(1)因为p在x轴上,
所以a+5=0,
所以a=﹣5.
∴2a﹣2=﹣12,
所以P(﹣12,0);
(2)因为直线PQ||y轴,
所以2a﹣2=4,
所以a=3.
所以a+5=8.
所以P(4,8),
∵点Q在第四象限,且PQ=10,
∴b=8﹣10=﹣2,
∴Q(4,﹣2).
19.解:(1)∵点A(﹣2,3),B(1,﹣3),
∴AB==3;
故答案为3;
(2)当B点在x轴上,设B(t,0),
而点A(﹣2,3),A、B两点间的距离是5,
∴(﹣2﹣t)2+(0﹣3)2=52,解得t=2或﹣6,
此时B点坐标为(2,0)或(﹣6,0);
当B点在y轴上,设B(0,m),
而点A(﹣2,3),A、B两点间的距离是5,
∴(0+2)2+(m﹣3)2=52,解得m=3+或3﹣,
此时B点坐标为(0,3+)或(0,3﹣);
综上所述,B点坐标为(2,0)或(﹣6,0)或(0,3+)或(0,3﹣);
(3)∵点A(x,3),B(3,x+1),且A、B两点间的距离是5,
∴(x﹣3)2+(3﹣x﹣1)2=52,
整理得x2﹣5x﹣6=0,
解得x1=﹣1,x2=6,
即x的值为﹣1或6.
20.解:(1)∵点A(a,﹣5),B(8,b)关于y轴对称,
∴a=﹣8,b=﹣5;
(2))∵点A(a,﹣5),B(8,b)关于x轴对称,
∴a=8,b=5;
(3)∵AB∥y轴,
∴a=8,b为不等于﹣5的实数;
(4)∵A,B两点在第二、第四象限的角平分线上,
∴a=5,b=﹣8.
21.解:(1)∵点P(3m﹣6,m+1)在y轴上,
∴3m﹣6=0,
解得m=2,
∴m+1=2+1=3,
∴点P的坐标为(0,3);
(2)点P(3m﹣6,m+1)在x轴上,
∴m+1=0,
解得m=﹣1,
∴3m﹣6=3×(﹣1)﹣6=﹣9,
∴点P的坐标为(﹣9,0);
(3)∵点P(3m﹣6,m+1)的纵坐标比横坐标大5,
∴m+1﹣(3m﹣6)=5,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
m+1=1+1=2,
∴点P的坐标为(﹣3,2);
(4)∵点P(3m﹣6,m+1)在过点A(﹣1,2)且与x轴平行的直线上,
∴m+1=2,
解得m=1,
∴3m﹣6=3×1﹣6=﹣3,
m+1=1+1=2,
∴点P的坐标为(﹣3,2).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
