人教七上数学1.2.1有理数有理数分类课件(19张ppt)
文档属性
| 名称 | 人教七上数学1.2.1有理数有理数分类课件(19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
知识回顾
1、在-2;+1/2;-3.5;11中,正数
是 ;负数是 。
2、+1350米表示高于海平面1350米,
低于海平面200米,记作 。
3、如果上升10米,记作+10米,
那么下降12米,记作 。
4、如果规定向西走30米,记作+30米,
那么-40米,表示 。
+1/2、 11
-2、 -3.5
向东走了40米
-12
米
-200
米
有理数
12.96,
182.5,
110,
12.91,
1.1,
-52
0,
+75,
122.5,
+10.
-7.5,
18,
305,
1.在以上各数中,哪些是在小学里学过的数 它们可以分为哪几类
2.在小学里学过的数中,有没有哪类数在上面没有出现 请举例说明.
3.用计算器计算下列各分数的值,说明所有分数都可以化作什么数
同桌探究
4.由前面的结论,小学里学的数可以分为哪几类
5.引入负数后,整数除了小学学的整数外,还包含其它的整数吗?
分数除了小学学的分数外,还包含其它的分数吗?
综合归纳 形成新知
活动2
零:
负分数:
-52, -67, -1,-2,…
0
正整数:
负整数:
正整数集合
正分数:
5
1
2
3
4
+10,18,29,+75,
12.96,
正分数集合
182.5,
12.91,
1.1,
-7.5,
110,305,1,2,3,…
182.5,
12.91,
1.1,
负整数集合
零
负分数集合
-7.5,
0
负分数
正分数
负整数
正整数
零
整数
分数
有理数
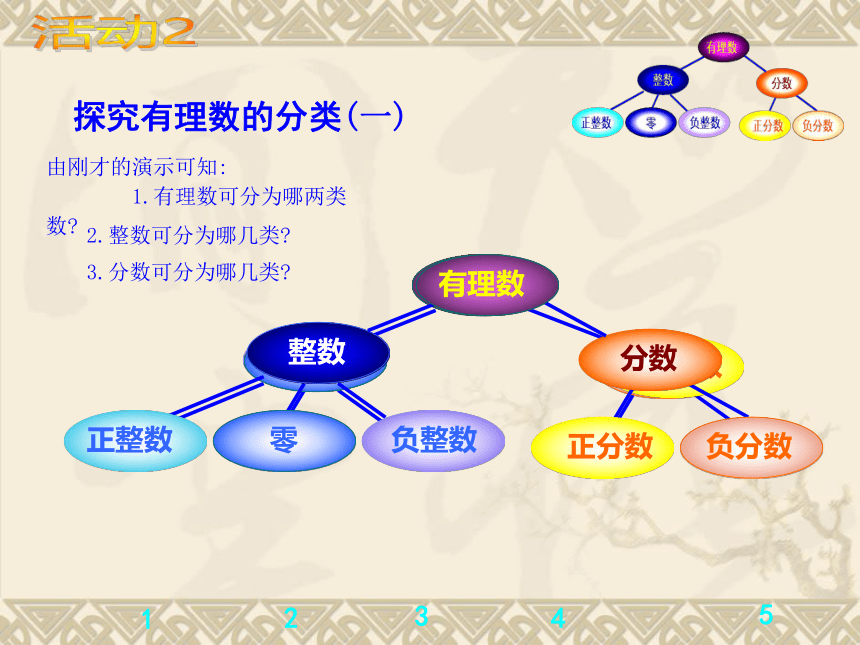
由刚才的演示可知:
1.有理数可分为哪两类数
探究有理数的分类(一)
2.整数可分为哪几类
3.分数可分为哪几类
1
2
3
4
5
负分数
正分数
负整数
正整数
零
整数
分数
有理数
1
2
3
6
5
4
-4
-2
-1
-3
0
-6
-5
⑧
①
②
③
④
⑤
⑥
⑦
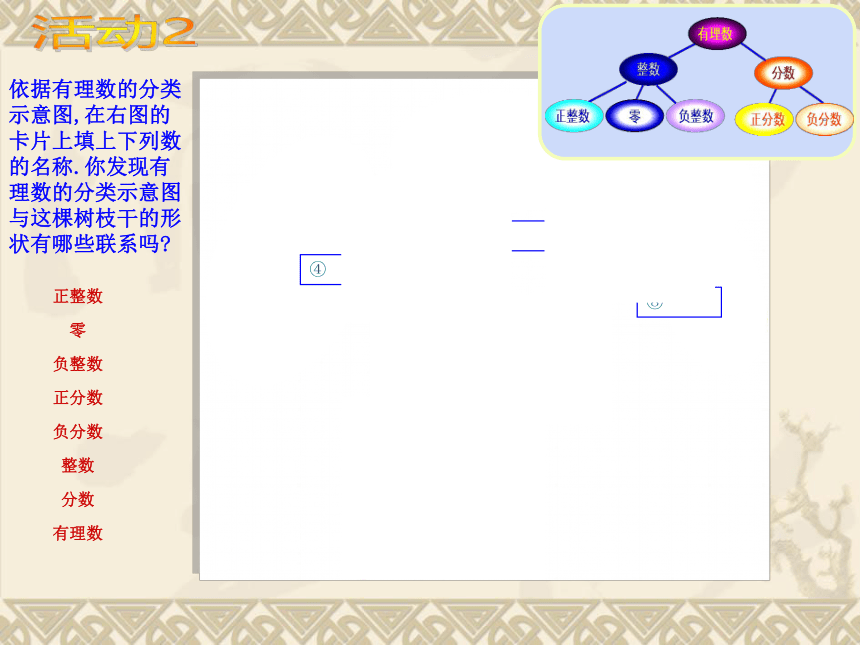
依据有理数的分类示意图,在右图的卡片上填上下列数的名称.你发现有理数的分类示意图与这棵树枝干的形状有哪些联系吗
正整数
零
负整数
正分数
负分数
整数
分数
有理数
分析探究 拓展新知
活动3
1.在左图的有理数中,正整数有:__________;负分数有:_____________________________;整数有:_______________________________;分数有:_______________________________.
探究有理数的分类(二)
1
2
3
4
5
2. 在做第1题时,发现了新的分类方法:带“+”的数分为一类,带“-”的数分为一类,数的前面没有符号的作为一类.你认为这种分类方法对吗 若对,你认为怎么命名?
小组探究
回归生活 应用新知
活动4
知识应用
1、把下列各数填入相应的集合内。
12/7,-3.1416,0,2008,-8/5, -0.23456,10%,10.1,0.67,-89
……
……
正数集合
负数集合
……
……
整数集合
分数集合
2008
10.1
0.67
-3.1416
-8/5
-0.23456
-89
12/7
10%
0
2008
-89
12/7
-3.1416
-8/5
-0.23456
10%
10.1
0.67
2、以下是两位同学给出的有理数的分类 方法,你认为他们的分类正确吗 ?
有理数
正有理数
负有理数
正整数
正分数
负整数
负分数
有
理
数
正数
整数
分数
负数
零
不能忘了零哦!
分类要有标准哦!
3、下列关于零的说法,正确的有 ( )
①0是最小的正整数
②0是最小的有理数
③0不是负数
④0既是非正数也是非负数
B
A、1个 B、2个 C、3个 D、4个
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
4、判 断
5、如果用一个字母表示一个数,那a可能是什么样的数?一定是正数吗?
答:不一定,a可能是正数,可能是负数,也可能是0。
探 究
巩固练习
2.填空:
(1)既是分数又是负数的数是_______;
(2)非负数包括________和_______;
(3)非正数包括________和_______;
(4)非负整数包括________和_______;又称为________;
(5)非负分数包括________和_______;
(6)非正分数包括________和_______;
(7)最小的正整数是______,最大的负整数是_____,所有大于-4的负整数有________,不大于3的非负整数有____________。
负分数
正数
0
0
负数
自然数
正整数
0
整数
正分数
整数
负分数
1
-1
-1,-2,-3
0,1,2,3
“分数=小数”成立吗?
1、分数与有限小数和无限循环小数可以互化。
例:31/5 = 6.2 , 10/3=3.33……
0.24 =6/25 , 0.66……=2/3
2、无限不循环小数不能化成分数;
分数也不可能化成无限不循环小数。
例: 不能化成分数。
3.010010001……也不能化成分数。
分数与小数是不一样的。
课堂小结
这节课我们的收获:
1、有理数的概念。
2、有理数的分类。
3、数学方法:分类思想。
我努力我成功
知识回顾
1、在-2;+1/2;-3.5;11中,正数
是 ;负数是 。
2、+1350米表示高于海平面1350米,
低于海平面200米,记作 。
3、如果上升10米,记作+10米,
那么下降12米,记作 。
4、如果规定向西走30米,记作+30米,
那么-40米,表示 。
+1/2、 11
-2、 -3.5
向东走了40米
-12
米
-200
米
有理数
12.96,
182.5,
110,
12.91,
1.1,
-52
0,
+75,
122.5,
+10.
-7.5,
18,
305,
1.在以上各数中,哪些是在小学里学过的数 它们可以分为哪几类
2.在小学里学过的数中,有没有哪类数在上面没有出现 请举例说明.
3.用计算器计算下列各分数的值,说明所有分数都可以化作什么数
同桌探究
4.由前面的结论,小学里学的数可以分为哪几类
5.引入负数后,整数除了小学学的整数外,还包含其它的整数吗?
分数除了小学学的分数外,还包含其它的分数吗?
综合归纳 形成新知
活动2
零:
负分数:
-52, -67, -1,-2,…
0
正整数:
负整数:
正整数集合
正分数:
5
1
2
3
4
+10,18,29,+75,
12.96,
正分数集合
182.5,
12.91,
1.1,
-7.5,
110,305,1,2,3,…
182.5,
12.91,
1.1,
负整数集合
零
负分数集合
-7.5,
0
负分数
正分数
负整数
正整数
零
整数
分数
有理数
由刚才的演示可知:
1.有理数可分为哪两类数
探究有理数的分类(一)
2.整数可分为哪几类
3.分数可分为哪几类
1
2
3
4
5
负分数
正分数
负整数
正整数
零
整数
分数
有理数
1
2
3
6
5
4
-4
-2
-1
-3
0
-6
-5
⑧
①
②
③
④
⑤
⑥
⑦
依据有理数的分类示意图,在右图的卡片上填上下列数的名称.你发现有理数的分类示意图与这棵树枝干的形状有哪些联系吗
正整数
零
负整数
正分数
负分数
整数
分数
有理数
分析探究 拓展新知
活动3
1.在左图的有理数中,正整数有:__________;负分数有:_____________________________;整数有:_______________________________;分数有:_______________________________.
探究有理数的分类(二)
1
2
3
4
5
2. 在做第1题时,发现了新的分类方法:带“+”的数分为一类,带“-”的数分为一类,数的前面没有符号的作为一类.你认为这种分类方法对吗 若对,你认为怎么命名?
小组探究
回归生活 应用新知
活动4
知识应用
1、把下列各数填入相应的集合内。
12/7,-3.1416,0,2008,-8/5, -0.23456,10%,10.1,0.67,-89
……
……
正数集合
负数集合
……
……
整数集合
分数集合
2008
10.1
0.67
-3.1416
-8/5
-0.23456
-89
12/7
10%
0
2008
-89
12/7
-3.1416
-8/5
-0.23456
10%
10.1
0.67
2、以下是两位同学给出的有理数的分类 方法,你认为他们的分类正确吗 ?
有理数
正有理数
负有理数
正整数
正分数
负整数
负分数
有
理
数
正数
整数
分数
负数
零
不能忘了零哦!
分类要有标准哦!
3、下列关于零的说法,正确的有 ( )
①0是最小的正整数
②0是最小的有理数
③0不是负数
④0既是非正数也是非负数
B
A、1个 B、2个 C、3个 D、4个
(1)0是整数( )
(2)自然数一定是整数( )
(3)0一定是正整数( )
(4)整数一定是自然数( )
√
√
×
×
4、判 断
5、如果用一个字母表示一个数,那a可能是什么样的数?一定是正数吗?
答:不一定,a可能是正数,可能是负数,也可能是0。
探 究
巩固练习
2.填空:
(1)既是分数又是负数的数是_______;
(2)非负数包括________和_______;
(3)非正数包括________和_______;
(4)非负整数包括________和_______;又称为________;
(5)非负分数包括________和_______;
(6)非正分数包括________和_______;
(7)最小的正整数是______,最大的负整数是_____,所有大于-4的负整数有________,不大于3的非负整数有____________。
负分数
正数
0
0
负数
自然数
正整数
0
整数
正分数
整数
负分数
1
-1
-1,-2,-3
0,1,2,3
“分数=小数”成立吗?
1、分数与有限小数和无限循环小数可以互化。
例:31/5 = 6.2 , 10/3=3.33……
0.24 =6/25 , 0.66……=2/3
2、无限不循环小数不能化成分数;
分数也不可能化成无限不循环小数。
例: 不能化成分数。
3.010010001……也不能化成分数。
分数与小数是不一样的。
课堂小结
这节课我们的收获:
1、有理数的概念。
2、有理数的分类。
3、数学方法:分类思想。
我努力我成功
