人教版 六年级上册数学 专题复习—计算 学案(无答案)
文档属性
| 名称 | 人教版 六年级上册数学 专题复习—计算 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 218.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 13:45:46 | ||
图片预览




文档简介
1、一个200米的跑道,分为4圈,每圈的宽度为1米,那么第一圈比第二圈多多少米?(π取3.14)
2、某市居民每月每户用水缴费方案如下表:
用水量 20立方米及以下 20立方米以上部分
收费标准 每立方米2.30元 每立方米3.45
根据以上有关信息完成:王大伯家今年5月份用水30立方米,王大伯家这个应缴水费多少元?
3、为了学生的卫生安全,学校给每个学生配一个水杯,每只水杯3元,美好家园打九折,汇集超市“买八送一”。学校想买180只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由。
4、一个旅游团共有287人,要租车到某地旅游,有两种车可供选择。54座的大巴车每辆租车费用432元,24座的中巴车每辆租车费用204元。要使每个旅客有有座位,又最省钱,应租多少大巴车,多少辆中巴车?
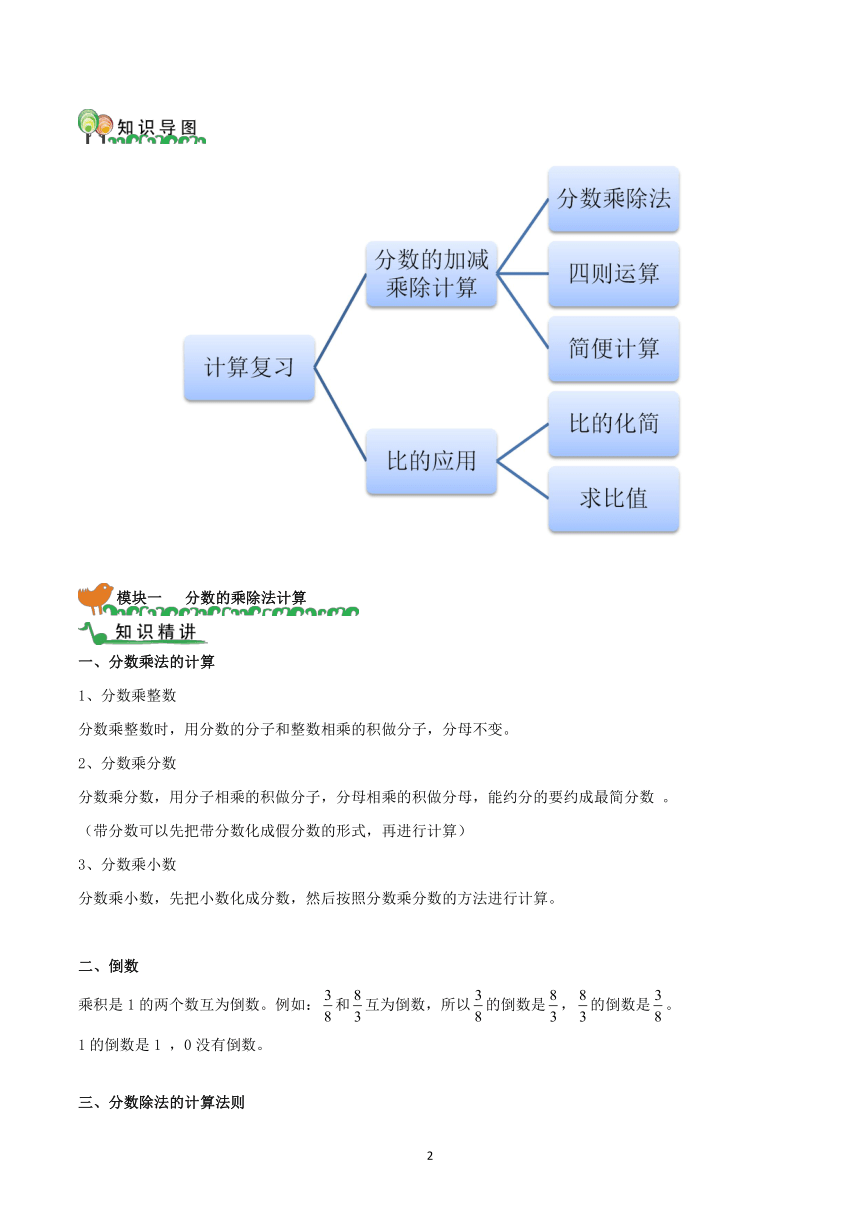
一、分数乘法的计算
1、分数乘整数
分数乘整数时,用分数的分子和整数相乘的积做分子,分母不变。
2、分数乘分数
分数乘分数,用分子相乘的积做分子,分母相乘的积做分母,能约分的要约成最简分数 。
(带分数可以先把带分数化成假分数的形式,再进行计算)
3、分数乘小数
分数乘小数,先把小数化成分数,然后按照分数乘分数的方法进行计算。
二、倒数
乘积是1的两个数互为倒数。例如:和互为倒数,所以的倒数是,的倒数是。
1的倒数是1 ,0没有倒数。
三、分数除法的计算法则
甲数除以乙数(0除外),就等于甲数乘乙数的倒数
1、分数除以整数时,被除数不变,乘号变为除号,整数变为它的倒数
2、分数除以分数时,被除数不变,乘号变为除号,除数变为它的倒数(带分数的先化为假分数)
3、分数除以小数时,先把小数化为分数,再乘这个分数的倒数
重难点:带分数或小数作为小数时,要先把带分数或小数化为分数后再利用分数乘除法法则进行计算。
易错点:分数计算结果要约分,假分数要化成带分数;除号变为乘号时,除数要相应地变为倒数,被除数不用化成倒数。
分数乘法的计算
分数乘整数
× 2 = × 4= ×5=
分数乘小数
× 7.5= ×2.4= ×2.5=
分数乘分数
× = 1× = 4× =
多个因数的分数乘法
×0.75× ×× 13 × ×
×5.7 × ××16 × ×
【巩固1】
×15= ×21= ×4=
×3.4= ×1.5= ×7.8=
×= × = ×=
×12× 2.4 ×× ××
倒数的认识
(1)( )的两个数叫做互为倒数, 的倒数是( );7的倒数是( );
( )没有倒数;1的倒数是( )。
(2)( )× = 9×( )=( )× = 1×( )= a×( )(a≠0)
(3)两个自然数的倒数的和为,这两个数分别是( )和( )。
【巩固2】 当a( )时,a的倒数一定大于a;当a( )时,a的倒数一定小于a;
当a( )时,a的倒数一定等a。
分数除法的计算
分数除以整数
= =
分数除以分数
分数除以小数
÷0.4= ÷1.9= ÷0.25=
【巩固3】
0.6÷= ÷0.6= ÷1.8=
分数的四则运算顺序和整数小数的运算顺序相同。有括号时,先算括号里面的再算括号外面的;无括号时,先算乘除再算加减;同级运算,先算前面的再算后面的。
重点:在混合运算中,同时出现分数和小数时,要注意统一化成分数或者小数。
易错点:涉及多个除数时,把乘号化成除号,把除数化成倒数容易遗漏其中一个
分数混合运算
3× ÷ ÷
[-(+)]÷ ×÷(-)
【巩固】分数混合运算
35× 14×÷14×
一、整数、小数、分数的简便计算同样可以用如下的运算定律、运算性质
运算定律 运算性质
加法交换律:a+b=b+a 减法运算性质:a-b-c=a-(b+c) a-(b-c)=a-b+c
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a 乘法结合律:a×b×c=a×(b×c) 乘法分配律:a×(b+c)=ab+ac 除法运算性质:a÷b÷c=a÷(b×c) a÷(b÷c)=a÷b×c (a+b)÷c=a÷c+b÷c (a-b)÷c=a÷c-b÷c
二、拆分法(也叫裂项法、拆项法)进行分数的简便运算。
运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。
(1)减法裂项:母积子差
=-;
=(-),
(2)加法裂项:母积子和
=+
加减法简算
【巩固5】加减法简算
分配律
×+ ×-
【巩固6】
乘法分配律的逆用
×37
【巩固7】×8 35×
减法裂项
(1)+++…..+
(2) +++…+
+++…+
加法裂项
比的基本性质
1、根据比、除法、分数的关系:
商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数时(0除外),分数值不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、最简整数比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
3、根据比的基本性质,可以把比化成最简单的整数比。
4.化简比和求比值的方法和区别:
计算方法 计算结果
化简比 用比的前项和后项同时除以它们的最大公因数。 用两个分数的比:用前项后项同时乘分母的最小公倍数,再按化简整数比的方法来化简。 两个小数的比:向右移动小数点的位置,先化成整数比再化简 是一个比 (通常化成最简单的整数比)
求比值 用比的前项除以后项 是一个数,可以是整数、分数或小数
重难点:化简比
易错点:化简比和求比值得区别
比的基本性质
(1)
(2)3:5的前项增加15,要使比值不变,后项应增加( ); 3:8的后项加上32,要使比值不变,前项应增加( )。
【巩固10】(1)4:5的前项扩大到原来的5倍,要使比值不变,后项应该( ),如果前项缩小到原来的3倍,要使比值不变,后项应该( )。
(2)2:7 的前项增加14,要使比值不变,后项应增加( );5∶12的前项增加15,要使比值不变,后项应增加( )。
化简比
21∶35 24∶32 ∶ ∶
0.8:0.32 0.3:0.15 0.6∶ 0.4∶
0.3吨∶150千克 0.4米∶60厘米 40分钟:小时
【巩固11】
54:45 1:0.5 9.1:182
:2.5 : 1.5 :16
20千克:吨 30分钟:小时 308立方厘米:2立方分米
求比值
36:18 24:30 0.6:0.24
: :
【巩固】35:120 0.7:0.42 :
0.3: 0.45: :0.75
四则运算:
× ×
简算:
×+ ×-
裂项
(1)+++ (2)
化简并求比值
0.7:0.42 :0.75
× = ××10 = ÷6= ×÷× =
×[(—)÷]
7.46×36+74.6×6.4
36×
+ ++ … + +++…+
先化简再求比值
105:135 9.1:18.2 :27
:2.5 0.625:1 480厘米:0.6米
500毫升:1.2升 20千克:吨 45分钟:小时
6
15
2、某市居民每月每户用水缴费方案如下表:
用水量 20立方米及以下 20立方米以上部分
收费标准 每立方米2.30元 每立方米3.45
根据以上有关信息完成:王大伯家今年5月份用水30立方米,王大伯家这个应缴水费多少元?
3、为了学生的卫生安全,学校给每个学生配一个水杯,每只水杯3元,美好家园打九折,汇集超市“买八送一”。学校想买180只水杯,请你当“参谋”,算一算:到哪家购买较合算?请写出你的理由。
4、一个旅游团共有287人,要租车到某地旅游,有两种车可供选择。54座的大巴车每辆租车费用432元,24座的中巴车每辆租车费用204元。要使每个旅客有有座位,又最省钱,应租多少大巴车,多少辆中巴车?
一、分数乘法的计算
1、分数乘整数
分数乘整数时,用分数的分子和整数相乘的积做分子,分母不变。
2、分数乘分数
分数乘分数,用分子相乘的积做分子,分母相乘的积做分母,能约分的要约成最简分数 。
(带分数可以先把带分数化成假分数的形式,再进行计算)
3、分数乘小数
分数乘小数,先把小数化成分数,然后按照分数乘分数的方法进行计算。
二、倒数
乘积是1的两个数互为倒数。例如:和互为倒数,所以的倒数是,的倒数是。
1的倒数是1 ,0没有倒数。
三、分数除法的计算法则
甲数除以乙数(0除外),就等于甲数乘乙数的倒数
1、分数除以整数时,被除数不变,乘号变为除号,整数变为它的倒数
2、分数除以分数时,被除数不变,乘号变为除号,除数变为它的倒数(带分数的先化为假分数)
3、分数除以小数时,先把小数化为分数,再乘这个分数的倒数
重难点:带分数或小数作为小数时,要先把带分数或小数化为分数后再利用分数乘除法法则进行计算。
易错点:分数计算结果要约分,假分数要化成带分数;除号变为乘号时,除数要相应地变为倒数,被除数不用化成倒数。
分数乘法的计算
分数乘整数
× 2 = × 4= ×5=
分数乘小数
× 7.5= ×2.4= ×2.5=
分数乘分数
× = 1× = 4× =
多个因数的分数乘法
×0.75× ×× 13 × ×
×5.7 × ××16 × ×
【巩固1】
×15= ×21= ×4=
×3.4= ×1.5= ×7.8=
×= × = ×=
×12× 2.4 ×× ××
倒数的认识
(1)( )的两个数叫做互为倒数, 的倒数是( );7的倒数是( );
( )没有倒数;1的倒数是( )。
(2)( )× = 9×( )=( )× = 1×( )= a×( )(a≠0)
(3)两个自然数的倒数的和为,这两个数分别是( )和( )。
【巩固2】 当a( )时,a的倒数一定大于a;当a( )时,a的倒数一定小于a;
当a( )时,a的倒数一定等a。
分数除法的计算
分数除以整数
= =
分数除以分数
分数除以小数
÷0.4= ÷1.9= ÷0.25=
【巩固3】
0.6÷= ÷0.6= ÷1.8=
分数的四则运算顺序和整数小数的运算顺序相同。有括号时,先算括号里面的再算括号外面的;无括号时,先算乘除再算加减;同级运算,先算前面的再算后面的。
重点:在混合运算中,同时出现分数和小数时,要注意统一化成分数或者小数。
易错点:涉及多个除数时,把乘号化成除号,把除数化成倒数容易遗漏其中一个
分数混合运算
3× ÷ ÷
[-(+)]÷ ×÷(-)
【巩固】分数混合运算
35× 14×÷14×
一、整数、小数、分数的简便计算同样可以用如下的运算定律、运算性质
运算定律 运算性质
加法交换律:a+b=b+a 减法运算性质:a-b-c=a-(b+c) a-(b-c)=a-b+c
加法结合律:a+b+c=a+(b+c)
乘法交换律:a×b=b×a 乘法结合律:a×b×c=a×(b×c) 乘法分配律:a×(b+c)=ab+ac 除法运算性质:a÷b÷c=a÷(b×c) a÷(b÷c)=a÷b×c (a+b)÷c=a÷c+b÷c (a-b)÷c=a÷c-b÷c
二、拆分法(也叫裂项法、拆项法)进行分数的简便运算。
运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。
(1)减法裂项:母积子差
=-;
=(-),
(2)加法裂项:母积子和
=+
加减法简算
【巩固5】加减法简算
分配律
×+ ×-
【巩固6】
乘法分配律的逆用
×37
【巩固7】×8 35×
减法裂项
(1)+++…..+
(2) +++…+
+++…+
加法裂项
比的基本性质
1、根据比、除法、分数的关系:
商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数时(0除外),分数值不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、最简整数比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
3、根据比的基本性质,可以把比化成最简单的整数比。
4.化简比和求比值的方法和区别:
计算方法 计算结果
化简比 用比的前项和后项同时除以它们的最大公因数。 用两个分数的比:用前项后项同时乘分母的最小公倍数,再按化简整数比的方法来化简。 两个小数的比:向右移动小数点的位置,先化成整数比再化简 是一个比 (通常化成最简单的整数比)
求比值 用比的前项除以后项 是一个数,可以是整数、分数或小数
重难点:化简比
易错点:化简比和求比值得区别
比的基本性质
(1)
(2)3:5的前项增加15,要使比值不变,后项应增加( ); 3:8的后项加上32,要使比值不变,前项应增加( )。
【巩固10】(1)4:5的前项扩大到原来的5倍,要使比值不变,后项应该( ),如果前项缩小到原来的3倍,要使比值不变,后项应该( )。
(2)2:7 的前项增加14,要使比值不变,后项应增加( );5∶12的前项增加15,要使比值不变,后项应增加( )。
化简比
21∶35 24∶32 ∶ ∶
0.8:0.32 0.3:0.15 0.6∶ 0.4∶
0.3吨∶150千克 0.4米∶60厘米 40分钟:小时
【巩固11】
54:45 1:0.5 9.1:182
:2.5 : 1.5 :16
20千克:吨 30分钟:小时 308立方厘米:2立方分米
求比值
36:18 24:30 0.6:0.24
: :
【巩固】35:120 0.7:0.42 :
0.3: 0.45: :0.75
四则运算:
× ×
简算:
×+ ×-
裂项
(1)+++ (2)
化简并求比值
0.7:0.42 :0.75
× = ××10 = ÷6= ×÷× =
×[(—)÷]
7.46×36+74.6×6.4
36×
+ ++ … + +++…+
先化简再求比值
105:135 9.1:18.2 :27
:2.5 0.625:1 480厘米:0.6米
500毫升:1.2升 20千克:吨 45分钟:小时
6
15
