2021-2022学年华东师大版数学八年级上册13.5.2线段的垂直平分线 课件(共17张ppt)
文档属性
| 名称 | 2021-2022学年华东师大版数学八年级上册13.5.2线段的垂直平分线 课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 898.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 12:25:40 | ||
图片预览





文档简介
(共17张PPT)
线段的垂直平分线
如图,小聪在A处,小明在B处,他们两人做抢礼物的游戏,请问:礼物放在何处游戏才公平?
创设情景 引入新知
2.尺规作已知线段AB的垂直平分线MN.
1.线段垂直平分线的定义:
并且 一条线段的直线称为这条线段的垂直平分线.
垂直 平分
如图:直线MN是线段AB的垂直平分线,
则MN⊥AB AO=BO
N
A
B
M
O
知 识 回 顾
A
B
PA=PB
Q
QA=QB
……
M
N
C
1.作线段AB的垂直平分线MN,垂足为C;
由此你能得出什么规律?
3.量一量PA、PB的长,你能发现什么?
2.在MN上任取一点P,连结PA、PB;
P
动手操作 探索新知
A
B
P
M
N
C
PA=PB
已知:如图,直线MN⊥AB,垂足为C, AC=CB,点P在MN上.
求证:
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB=90°
在 ΔPAC和Δ PBC中,
AC=BC
∠PCA=∠PCB
PC=PC
∴ ΔPAC ≌ΔPBC
∴PA=PB
猜想:线段垂直平分线上的点到线段两端点的距离相等.
验证猜想 探索性质
A
B
P
M
N
C
PA=PB
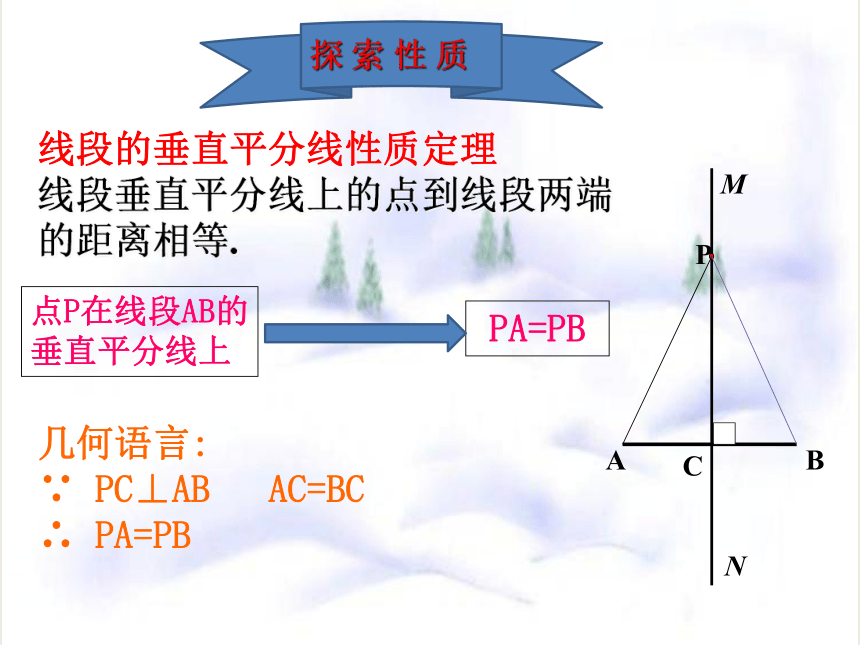
点P在线段AB的垂直平分线上
几何语言:
∵ PC⊥AB AC=BC
∴ PA=PB
线段的垂直平分线性质定理
线段垂直平分线上的点到线段两端的距离相等.
探 索 性 质
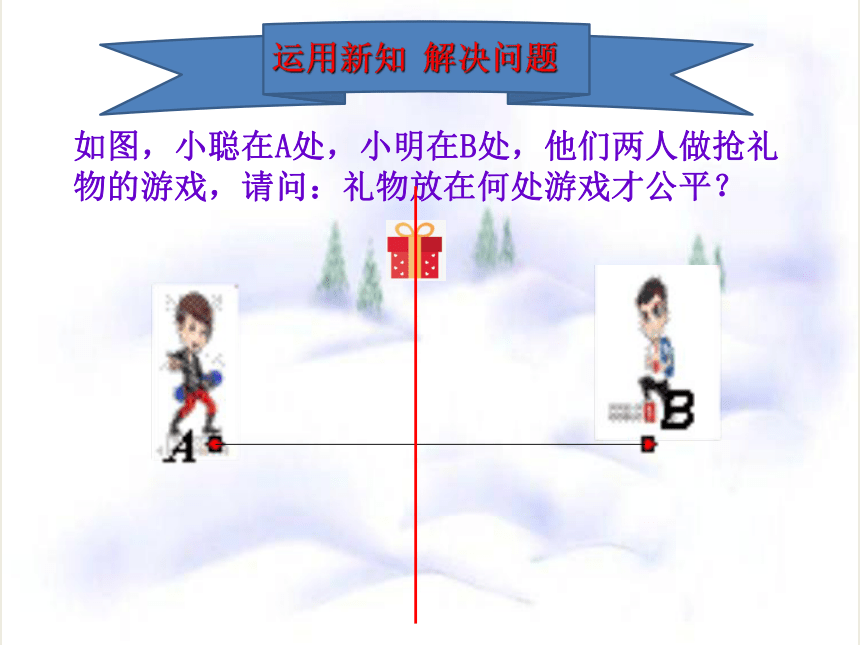
如图,小聪在A处,小明在B处,他们两人做抢礼物的游戏,请问:礼物放在何处游戏才公平?
运用新知 解决问题
性质定理逆命题:
到线段两端距离相等的点在线段的垂直平分线上
条件 结论
性质定理
逆命题
一个点在一条线段的垂直平分线上
该点到线段两端点的距离相等
一点到线段两端点的距离相等
该点在这条线段的垂直平分线上
你能写出线段垂直平分线性质定理的逆命题吗?
真命题
前 知 运 用
已知:如图,QA=QB.
求证:点P在线段AB的垂直平分线上.
N
A
B
Q
M
C
∴点Q在线段AB的垂直平分线上.
证明:过点Q作MN⊥AB,垂足为C,
则∠QCA=∠QCB=90°.
在Rt△QCA和Rt△QCB中
∵QA=QB
QC=QC
∴Rt△QCA≌Rt△QCB (H.L. ).
∴AC=BC(全等三角形的对应边相等).
到线段两端距离相等的点在线段的垂直平分线上
逆定理
剪一个三角形纸片通过折叠找出每条边的垂直平分线,你有什么发现?
动手做一做,你能发现什么?
点拨:要证明三条垂直平分线相交于一点,只要证明其中两条垂直平分线的交点在第三条直线上即可
A
O
C
B
m
n
l
三角形三条边的垂直平分线相交于一点.
命题:三角形三条边的垂直平分线相交于一点.
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点P
求证:点P也在AC的垂直平分线上
证明:连接AP,BP,CP.
∵点P在线段AB的垂直平分线上,
∴PA=PB
同理,PB=PC.
∴PA=PC.
∴点P在线段AB的垂直平分线上,
∴AB,BC,AC的垂直平分线相交于一点.
A
B
C
P
某市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等
A
B
C
运用新知 解决问题
B
A
C
求作一点P,使它到△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题中的数学思想
2.如图,BD⊥AC,垂足为点E,AE=CE.
求证:AB+CD=AD+BC.
3. 如图,在△ABC中,已知点D在BC上,且BD+AD=BC.
求证:点D在AC的垂直平分线上.
A
B
D
C
学 以 致 用
小 结
这节课你学习了什么 有何收获 有何困惑
线段垂直平分线上的点到线段两端的距离相等.
到线段两端距离相等的点在线段的垂直平分线上
互逆定理
※ 线段的垂直平分线可以看作是点到线段两端点 距离相等的所有点的集合.
※ 三角形三边的垂直平分线交于一点.
作 业
书面作业:
1.逆定理的证明(作平分,证垂直)
2.课本105页12题
预习作业:
课本96-98页,《角平分线》,初步了解角平分线的性质定理及判断定理.
谢谢指导!
线段的垂直平分线
如图,小聪在A处,小明在B处,他们两人做抢礼物的游戏,请问:礼物放在何处游戏才公平?
创设情景 引入新知
2.尺规作已知线段AB的垂直平分线MN.
1.线段垂直平分线的定义:
并且 一条线段的直线称为这条线段的垂直平分线.
垂直 平分
如图:直线MN是线段AB的垂直平分线,
则MN⊥AB AO=BO
N
A
B
M
O
知 识 回 顾
A
B
PA=PB
Q
QA=QB
……
M
N
C
1.作线段AB的垂直平分线MN,垂足为C;
由此你能得出什么规律?
3.量一量PA、PB的长,你能发现什么?
2.在MN上任取一点P,连结PA、PB;
P
动手操作 探索新知
A
B
P
M
N
C
PA=PB
已知:如图,直线MN⊥AB,垂足为C, AC=CB,点P在MN上.
求证:
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB=90°
在 ΔPAC和Δ PBC中,
AC=BC
∠PCA=∠PCB
PC=PC
∴ ΔPAC ≌ΔPBC
∴PA=PB
猜想:线段垂直平分线上的点到线段两端点的距离相等.
验证猜想 探索性质
A
B
P
M
N
C
PA=PB
点P在线段AB的垂直平分线上
几何语言:
∵ PC⊥AB AC=BC
∴ PA=PB
线段的垂直平分线性质定理
线段垂直平分线上的点到线段两端的距离相等.
探 索 性 质
如图,小聪在A处,小明在B处,他们两人做抢礼物的游戏,请问:礼物放在何处游戏才公平?
运用新知 解决问题
性质定理逆命题:
到线段两端距离相等的点在线段的垂直平分线上
条件 结论
性质定理
逆命题
一个点在一条线段的垂直平分线上
该点到线段两端点的距离相等
一点到线段两端点的距离相等
该点在这条线段的垂直平分线上
你能写出线段垂直平分线性质定理的逆命题吗?
真命题
前 知 运 用
已知:如图,QA=QB.
求证:点P在线段AB的垂直平分线上.
N
A
B
Q
M
C
∴点Q在线段AB的垂直平分线上.
证明:过点Q作MN⊥AB,垂足为C,
则∠QCA=∠QCB=90°.
在Rt△QCA和Rt△QCB中
∵QA=QB
QC=QC
∴Rt△QCA≌Rt△QCB (H.L. ).
∴AC=BC(全等三角形的对应边相等).
到线段两端距离相等的点在线段的垂直平分线上
逆定理
剪一个三角形纸片通过折叠找出每条边的垂直平分线,你有什么发现?
动手做一做,你能发现什么?
点拨:要证明三条垂直平分线相交于一点,只要证明其中两条垂直平分线的交点在第三条直线上即可
A
O
C
B
m
n
l
三角形三条边的垂直平分线相交于一点.
命题:三角形三条边的垂直平分线相交于一点.
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点P
求证:点P也在AC的垂直平分线上
证明:连接AP,BP,CP.
∵点P在线段AB的垂直平分线上,
∴PA=PB
同理,PB=PC.
∴PA=PC.
∴点P在线段AB的垂直平分线上,
∴AB,BC,AC的垂直平分线相交于一点.
A
B
C
P
某市政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等
A
B
C
运用新知 解决问题
B
A
C
求作一点P,使它到△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题中的数学思想
2.如图,BD⊥AC,垂足为点E,AE=CE.
求证:AB+CD=AD+BC.
3. 如图,在△ABC中,已知点D在BC上,且BD+AD=BC.
求证:点D在AC的垂直平分线上.
A
B
D
C
学 以 致 用
小 结
这节课你学习了什么 有何收获 有何困惑
线段垂直平分线上的点到线段两端的距离相等.
到线段两端距离相等的点在线段的垂直平分线上
互逆定理
※ 线段的垂直平分线可以看作是点到线段两端点 距离相等的所有点的集合.
※ 三角形三边的垂直平分线交于一点.
作 业
书面作业:
1.逆定理的证明(作平分,证垂直)
2.课本105页12题
预习作业:
课本96-98页,《角平分线》,初步了解角平分线的性质定理及判断定理.
谢谢指导!
