华师大版九年级数学26.2.3求二次函数的表达式(word版含答案)
文档属性
| 名称 | 华师大版九年级数学26.2.3求二次函数的表达式(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 51.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览

文档简介
华师大版九年级数学26章 专题求二次函数的表达式 含答案
1.抛物线的函数表达式为y=3(x-2)2+1,若将x轴向上平移2个单位长度,将y轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )
A.y=3(x+1)2+3 B.y=3(x-5)2+3
C.3(x-5)2-1 D.y=3(x+1)2-1
2.已知二次函数的图象过(-1,5)、(1,1)和(3,5)三个点,则这个二次函数的表达式为( )
3.已知抛物线的顶点坐标为(-1,-2),且过点(1,10),则这条抛物线的表达式为( )
A.y=3(x-1)2-2 B.y=3(x+1)2+2
C.y=3(x+1)2-2 D.y=-3(x+1)2+3
4.把函数y=(x-1)2+2的图象向右平移1个单位长度,平移后图象的函数表达式为( )
A.y=x2+2 B.y=(x-1)2+1 C.y=(x-2)2+2 D.y=(x-1)2+3
5.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线的表达式应变为 ( )
A.y=(x-2)2+3 B.y=(x-2)2+5 C. y=x2-1 D.y=x2+4
6.抛物线y=ax2+bx+c经过点(3,0)和(2,3),且以直线x=1为对称轴,则它的表达式为 ( )
A.y=x2-2x-3 B.y=x2-2x-3 C.y=x2-2x+3 D.y=-x2+2x-3
7.以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14 B.y=x2-8x+14 C.y=x2+4x+3 D.y=x2-4x+3
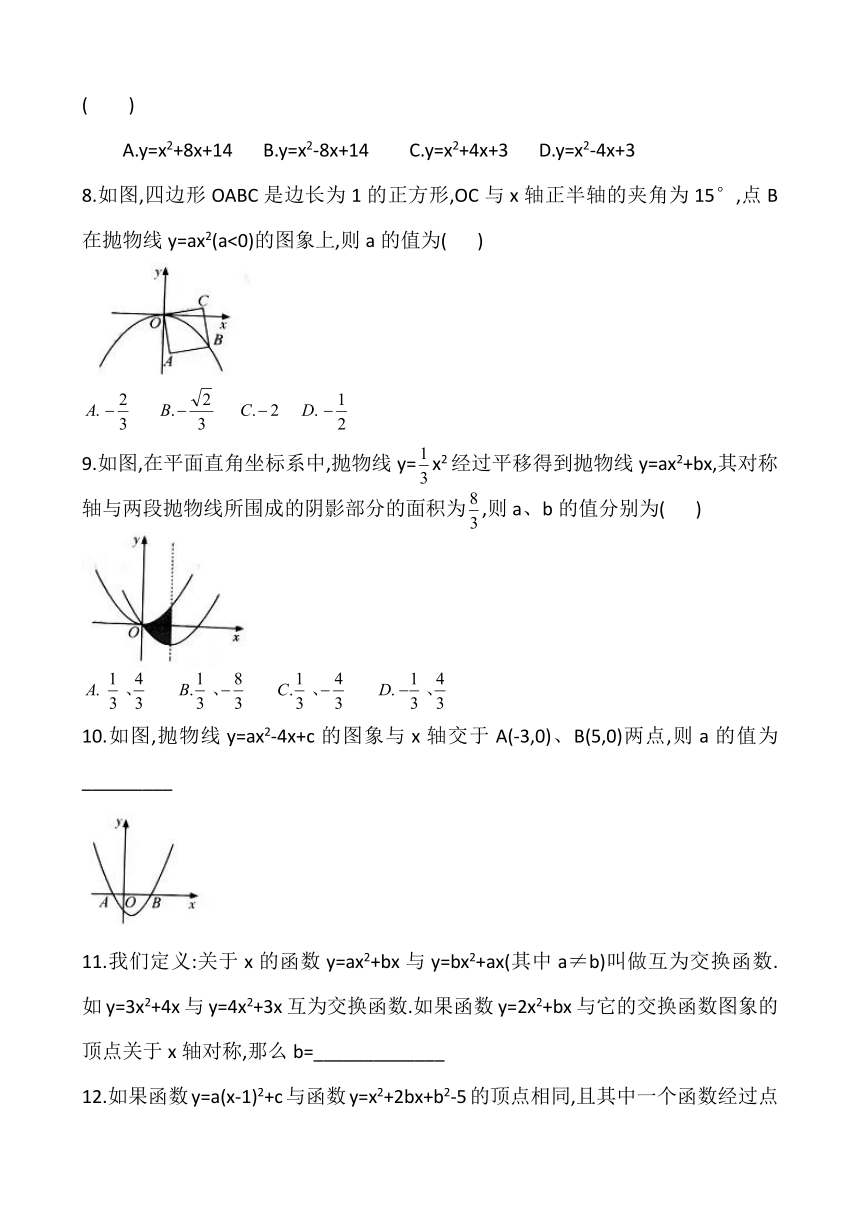
8.如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
9.如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为,则a、b的值分别为( )
10.如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为_________
11.我们定义:关于x的函数y=ax2+bx与y=bx2+ax(其中a≠b)叫做互为交换函数.如y=3x2+4x与y=4x2+3x互为交换函数.如果函数y=2x2+bx与它的交换函数图象的顶点关于x轴对称,那么b=_____________
12.如果函数y=a(x-1)2+c与函数y=x2+2bx+b2-5的顶点相同,且其中一个函数经过点(2,7),求这两个函数的表达式__________
13.如图,抛物线y=-x2+bx+5与x轴交于A、B两点
(1)若过点C的直线x=2是抛物线的对称轴,求抛物线的表达式
(2)当b≥4,0≤x≤2时,函数值y的最大值满足3≤y≤15,求b的取值范围
14.已知抛物线y=ax2-4ax-5a(a>0)与x轴交于A、B两点,点A在点B的左侧
(1)求抛物线的对称轴和点A、B的坐标
(2)当3≤x≤4时,y有最小值为-4,求抛物线的表达式
(3)已知点E(-1,1)、F(6,4a+1),且抛物线与线段EF只有一个公共点,请求出a的取值范围
答案
1.C
2.B
3.C
4.C
5.C
6.B
7.A
8.B
9.C
10.2
11.-2
12.y=12x2-24x+7.
13.y=-x2+4x+5
14.解:(1)点A的坐标为(-1,0),点B的坐标为(5,0)
(2)
(3)a的取值范围为a≥
1.抛物线的函数表达式为y=3(x-2)2+1,若将x轴向上平移2个单位长度,将y轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )
A.y=3(x+1)2+3 B.y=3(x-5)2+3
C.3(x-5)2-1 D.y=3(x+1)2-1
2.已知二次函数的图象过(-1,5)、(1,1)和(3,5)三个点,则这个二次函数的表达式为( )
3.已知抛物线的顶点坐标为(-1,-2),且过点(1,10),则这条抛物线的表达式为( )
A.y=3(x-1)2-2 B.y=3(x+1)2+2
C.y=3(x+1)2-2 D.y=-3(x+1)2+3
4.把函数y=(x-1)2+2的图象向右平移1个单位长度,平移后图象的函数表达式为( )
A.y=x2+2 B.y=(x-1)2+1 C.y=(x-2)2+2 D.y=(x-1)2+3
5.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线的表达式应变为 ( )
A.y=(x-2)2+3 B.y=(x-2)2+5 C. y=x2-1 D.y=x2+4
6.抛物线y=ax2+bx+c经过点(3,0)和(2,3),且以直线x=1为对称轴,则它的表达式为 ( )
A.y=x2-2x-3 B.y=x2-2x-3 C.y=x2-2x+3 D.y=-x2+2x-3
7.以矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A.y=x2+8x+14 B.y=x2-8x+14 C.y=x2+4x+3 D.y=x2-4x+3
8.如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )
9.如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为,则a、b的值分别为( )
10.如图,抛物线y=ax2-4x+c的图象与x轴交于A(-3,0)、B(5,0)两点,则a的值为_________
11.我们定义:关于x的函数y=ax2+bx与y=bx2+ax(其中a≠b)叫做互为交换函数.如y=3x2+4x与y=4x2+3x互为交换函数.如果函数y=2x2+bx与它的交换函数图象的顶点关于x轴对称,那么b=_____________
12.如果函数y=a(x-1)2+c与函数y=x2+2bx+b2-5的顶点相同,且其中一个函数经过点(2,7),求这两个函数的表达式__________
13.如图,抛物线y=-x2+bx+5与x轴交于A、B两点
(1)若过点C的直线x=2是抛物线的对称轴,求抛物线的表达式
(2)当b≥4,0≤x≤2时,函数值y的最大值满足3≤y≤15,求b的取值范围
14.已知抛物线y=ax2-4ax-5a(a>0)与x轴交于A、B两点,点A在点B的左侧
(1)求抛物线的对称轴和点A、B的坐标
(2)当3≤x≤4时,y有最小值为-4,求抛物线的表达式
(3)已知点E(-1,1)、F(6,4a+1),且抛物线与线段EF只有一个公共点,请求出a的取值范围
答案
1.C
2.B
3.C
4.C
5.C
6.B
7.A
8.B
9.C
10.2
11.-2
12.y=12x2-24x+7.
13.y=-x2+4x+5
14.解:(1)点A的坐标为(-1,0),点B的坐标为(5,0)
(2)
(3)a的取值范围为a≥
