4.3.2.1等比数列的前n项和(知识梳理+例题+变式+练习)(解析版)
文档属性
| 名称 | 4.3.2.1等比数列的前n项和(知识梳理+例题+变式+练习)(解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 16:01:58 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
4.3.2.1等比数列的前n项和
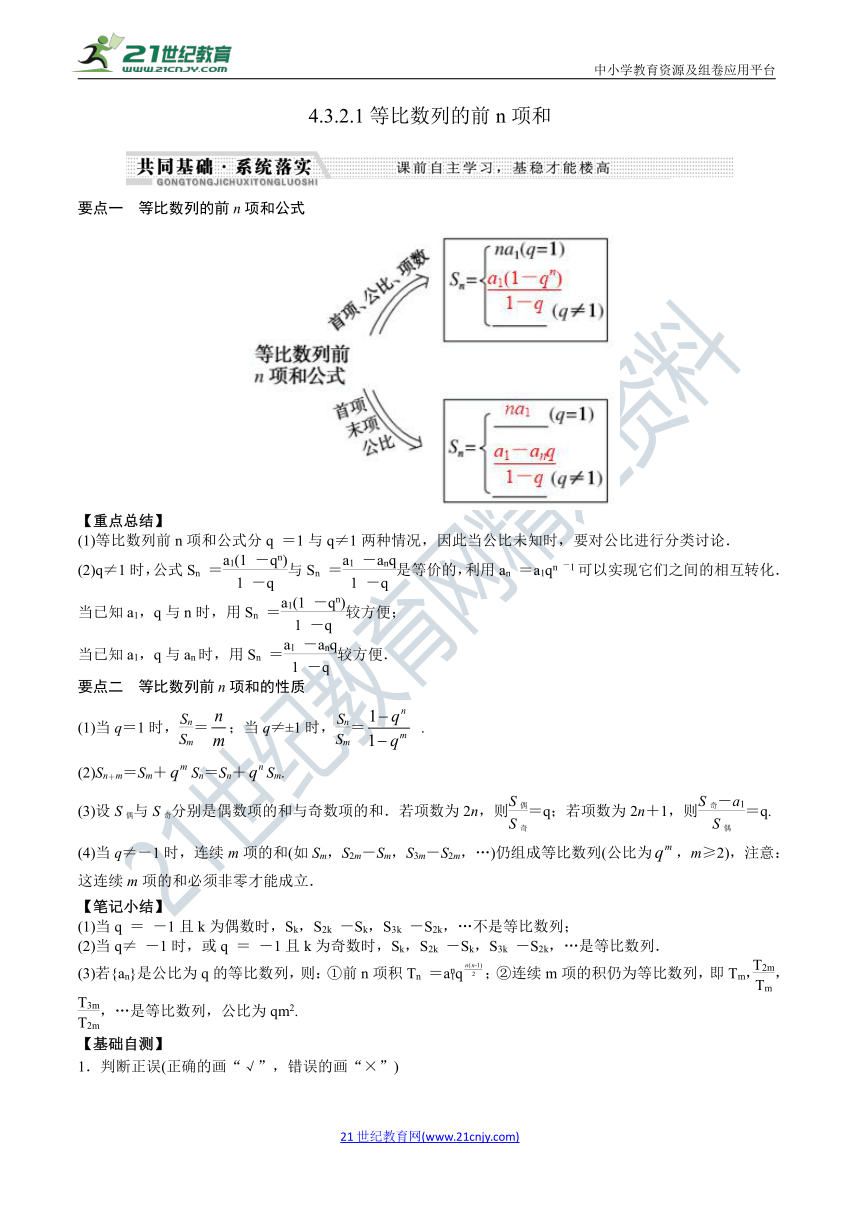
要点一 等比数列的前n项和公式
【重点总结】
(1)等比数列前n项和公式分q =1与q≠1两种情况,因此当公比未知时,要对公比进行分类讨论.
(2)q≠1时,公式Sn =与Sn =是等价的,利用an =a1qn -1可以实现它们之间的相互转化.
当已知a1,q与n时,用Sn =较方便;
当已知a1,q与an时,用Sn =较方便.
要点二 等比数列前n项和的性质
(1)当q=1时,=;当q≠±1时,= .
(2)Sn+m=Sm+Sn=Sn+Sm.
(3)设S偶与S奇分别是偶数项的和与奇数项的和.若项数为2n,则=q;若项数为2n+1,则=q.
(4)当q≠-1时,连续m项的和(如Sm,S2m-Sm,S3m-S2m,…)仍组成等比数列(公比为,m≥2),注意:这连续m项的和必须非零才能成立.
【笔记小结】
(1)当q = -1且k为偶数时,Sk,S2k -Sk,S3k -S2k,…不是等比数列;
(2)当q≠ -1时,或q = -1且k为奇数时,Sk,S2k -Sk,S3k -S2k,…是等比数列.
(3)若{an}是公比为q的等比数列,则:①前n项积Tn =aq;②连续m项的积仍为等比数列,即Tm,,,…是等比数列,公比为qm2.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)求等比数列{an}的前n项和时可直接套用公式Sn=来求.( )
(2)若首项为a的数列既是等差数列又是等比数列,则其前n项和为Sn=na.( )
(3)若某数列的前n项和公式为Sn=-aqn+a(a≠0,q≠0且q≠1,n∈N*),则此数列一定是等比数列.( )
(4)若Sn为等比数列的前n项和,则S3,S6,S9成等比数列.( )
【答案】(1)×(2)√(3)√(4)×
2.已知等比数列{an}的首项a1=3,公比q=2,则S5等于( )
A.93 B.-93
C.45 D.-45
【答案】A
【解析】S5===93.故选A.
3.已知等比数列{an}的前n项和为Sn,若S3=1,S6=9,则公比q=________.
【答案】2
【解析】S6-S3=a4+a5+a6=(a1+a2+a3)q3=S3·q3=1×q3=8.∴q=2.
题型一 等比数列前n项和的基本运算
【例1】在等比数列{an}中,
(1)S2=30,S3=155,求Sn;
(2)a1+a3=10,a4+a6=,求S5;
(3)a1+an=66,a2an-1=128,Sn=126,求q.
【解析】(1)由题意知
解得或
从而Sn=×5n+1-或Sn=
(2)法一:由题意知
解得从而S5==.
法二:由(a1+a3)q3=a4+a6,
得q3=,从而q=.
又a1+a3=a1(1+q2)=10,
所以a1=8,从而S5==.
(3)因为a2an-1=a1an=128,
所以a1,an是方程x2-66x+128=0的两根.
从而或
又Sn==126,所以q为2或.
【方法归纳】
(1)在等比数列{an}的五个量a1,q,an,n,Sn中,已知其中的三个量,通过列方程组,就能求出另外两个量,这是方程思想与整体思想在数列中的具体应用.
(2)在解决与前n项和有关的问题时,首先要对公比q=1或q≠1进行判断,若两种情况都有可能,则要分类讨论.
【跟踪训练】在等比数列{an}中,
(1)若a1=,an=16,Sn=11,求n和q;
(2)已知S4=1,S8=17,求an.
【解析】(1)由Sn=得11=,∴q=-2,
又由an=a1qn-1得16=(-2)n-1,∴n=5.
(2)若q=1,则S8=2S4,不合题意,
∴q≠1,∴S4==1,S8==17,
两式相除得=17=1+q4,
∴q=2或q=-2,∴a1=或a1=-,
∴an=·2n-1或-·(-2)n-1.
题型二 等比数列前n项和性质的应用
【例2】等比数列{an}的前n项和为Sn,S2=7,S6=91,则S4为( )
A.28 B.32
C.21 D.28或-21
【解析】∵{an}为等比数列,∴S2,S4-S2,S6-S4也为等比数列,
即7,S4-7,91-S4成等比数列,
∴(S4-7)2=7(91-S4),解得S4=28或S4=-21.
∵S4=a1+a2+a3+a4=a1+a2+a1q2+a2q2
=(a1+a2)(1+q2)=S2(1+q2)>S2,∴S4=28.故选A.
【变式训练1】将本例中“S2=7,S6=91”换为“正数等比数列中Sn=2,S3n=14”,则S4n=________.
【答案】30
【解析】设S2n=x,S4n=y,则2,x-2,14-x,y-14成等比数列,所以
所以或(舍去),所以S4n=30.
【例3】等比数列{an}中,公比q=3,S80=32,则a2+a4+a6+…+a80=________.
【答案】24
【解析】设S1=a2+a4+a6+…+a80,
S2=a1+a3+a5+…+a79.则=q=3,即S1=3S2.
又S1+S2=S80=32,∴S1=32,解得S1=24.
即a2+a4+a6+…+a80=24.
【方法技巧】考虑 =q,及S2n =S奇 +S偶.
【变式探究2】本例中的“q=3,S80=32.”改为“项数为偶数的等比数列,它的偶数项之和是奇数项之和的,又它的首项为,且中间两项的和为”,则等比数列的项数为________.
【答案】12
【解析】设等比数列为{an},项数为2n,一个项数为2n的等比数列中,=q,则q=,
又an和an+1为中间两项,则an+an+1=,即a1qn-1+a1qn=,又a1=,q=,
∴·n-1+·n= ·n-1·= n=6.
∴项数为2n=12.
则此等比数列的项数为12.
【方法归纳】
(1)在涉及奇数项和S奇与偶数项和S偶时,常考虑其差或比进行简化运算.若项数为2n,则=q(S奇≠0);若项数为2n+1,则=q(S偶≠0).
(2)等比数列前n项和为Sn(且Sn≠0),则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn(q≠-1).
题型三 an与Sn关系的应用
【例4】设数列{an}的前n项和为Sn.已知a1=1,a2=2,且an+2=3Sn-Sn+1+3,
(1)证明:an+2=3an;
(2)求Sn.
【解析】(1)证明:由已知,an+2=3Sn-Sn+1+3,
因而对任意n∈N*,n≥2,有
an+1=3Sn-1-Sn+3.
两式相减,得an+2-an+1=3an-an+1,
即an+2=3an,n≥2.
又因为a1=1,a2=2,所以a3=3S1-S2+3=3a1-(a1+a2)+3=3a1.
故对一切n∈N*,an+2=3an.
(2)由(1)知,an≠0,所以=3,
于是数列{a2n-1}是首项a1=1,公比为3的等比数列;数列{a2n}是首项a2=2,公比为3的等比数列.因此a2n-1=3n-1,a2n=2×3n-1.
于是S2n=a1+a2+…+a2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)=(1+3+…+3n-1)+2(1+3+…+3n-1)=3(1+3+…+3n-1)=,从而S2n-1=S2n-a2n=-2×3n-1=(5×3n-2-1).
综上所述,Sn=
【方法归纳】
由an=Sn-Sn-1(n≥2),进行转化,得到an+2=3an.
由an+2=3an知{an}是由两个等比数列构成,所以求Sn时要分奇数项与偶数项和,并且要注意对n是奇数和偶数时讨论.
【跟踪训练2】若数列{an}的前n项和Sn=an+,则an=________.
【答案】(-2)n-1
【解析】由an=Sn-Sn-1(n≥2)
得an=-2an-1(n≥2)
∴=-2(n≥2)
又a1=1,∴an=(-2)n-1,
经检验当n=1时,上式也适合,∴an=(-2)n-1.
【易错辨析】忽略对公比q的讨论致误
【例5】已知等比数列{an}中,a1=2,S3=6,a3=________.
【答案】2或8
【解析】若q=1,则S3=3a1=6,符合题意,此时a3=a1=2.
若q≠1时,则 S3===6,
解得q=-2,此时a3=a1q2=2×(-2)2=8.
综上a3的值为2或8.
【易错警示】
1出错原因
忽略了对公比q的讨论,直接使用了等比数列的前n项和公式Sn=,从而漏解致误.
2.纠错心得
解答有关等比数列求和问题时,应考虑公比q两种情况q=1或q≠1,否则容易出错.
一、单选题
1.已知等比数列的前n项和为,若,,则( )
A.-2或3 B.-2 C.3 D.
【答案】C
【分析】
用等比数列的基本量表示出,然后代入条件计算得答案.
【解析】
由题可知,
∵,,,
∴,,
∵,,
∴,
∴,
∴.
故选:C.
2.数列,满足,,,则数列的前10项和为( )
A. B.
C. D.
【答案】B
【分析】
根据题干所给条件写出数列,的通项公式,并写出数列,得知数列是等比数列,再用等比数列的前n项和公式即可.
【解析】
∵数列,满足,,,
∴数列是等差数列,首项是2且公差是2,是等比数列,首项是2且公比是2,
∴数列的通项公式为,
数列的通项公式为,
则数列为,设,则,
∴数列是等比数列,且公比为4,首项为4.
则数列的前10项和为,
即数列的前10项和为.
故选:B.
3.设为等比数列的前项和,已知,,则公比( )
A.3 B.4 C.5 D.6
【答案】B
【分析】
根据题干所给条件列式并联立计算即可.
【解析】
设等比数列的第一项为,则,,
因为,则,得①
因为,则,得②
式子①-②,得,显然,,则.
故选:B.
4.数列中,,对任意,若,则( )
A.2 B.3 C.4 D.5
【答案】C
【分析】
取,可得出数列是等比数列,求得数列的通项公式,利用等比数列求和公式可得出关于的等式,由可求得的值.
【解析】
在等式中,令,可得,,
所以,数列是以为首项,以为公比的等比数列,则,
,
,则,解得.
故选:C.
5.设数列满足,则数列的前n项和为( )
A. B.
C. D.
【答案】C
【分析】
由题得(1), ,(2),两式相减求出即得解.
【解析】
由题得(1),
又 (2),
(2)-(1)得适合.
所以,所以数列是以为首项,以的等比数列,
所以.
故选:C
6.定义表示不超过的最大整数,如,.若数列的通项公式为,则( )
A. B. C. D.
【答案】A
【分析】
由题可得当时,含有个数列中的项,又,再利用错位相减法即求.
【解析】
由题知当时,含有个数列中的项,
又,
所以,
两边同乘以,得,
两式相减,得
,
所以.
故选:.
7.给出命题:若(,,都是与无关的常数)等比数列的前项和,则.在这个命题的逆命题、否命题、逆否命题中,真命题的个数是( )
A. B. C. D.
【答案】C
【分析】
根据公式得到原命题为真,故逆否命题为真,举出反例恒等于得到逆命题和否命题为假,得到答案.
【解析】
因为,所以;
当时,,
由于是等比数列,所以对也适合,
所以,化简得,所以原命题是真命题,
因此逆否命题也是真命题;
反之,当时,满足,但此时恒等于,不可能是等比数列的前项和,所以逆命题是假命题,因此,否命题也是假命题.
故选:C.
8.已知数列的前项和为,且满足,若对于任意的,不等式恒成立,则实数的取值范围为( )
A. B.
C. D.
【答案】A
【分析】
首先根据题意求出,从而得到;再由对于任意的,不等式恒成立,得到不等式在时恒成立,从而得到,通过解不等式组即可求出实数的取值范围.
【解析】
因为,所以时,,
两式相减,得,即,
又时,,所以,
因为也适合,所以.
所以,
因为对于任意的,不等式恒成立,
所以对于任意的,不等式恒成立,
即对于任意的,不等式恒成立,
所以只需,即,解得或.
所以实数的取值范围为.
故选:A.
二、多选题
9.在等比数列中,公比,是数列的前n项和,若,,则下列结论正确的是( )
A. B.
C.数列是等比数列 D.数列是公差为2的等差数列
【答案】BC
【分析】
利用已知结合等比数列的通项公式求公比,进而写出通项公式、前n项和公式,结合各选项判断正误即可.
【解析】
由题设,,即,
由可得:,
∴,,
∴且公差为;且.
综上,A、D错误,B、C正确.
故选:BC
10.分形几何学是一门以不规则几何形态为研究对象的几何学,分形几何具有自身相似性,从它的任何一个局部经过放大,都可以得到一个和整体全等的图形如下图的雪花曲线,将一个边长为的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3),记为第个图形的边长,记为第个图形的周长,为的前项和,则下列说法正确的是( )
A.
B.
C.若,为中的不同两项,且,则最小值是
D.若恒成立,则的最小值为
【答案】AD
【分析】
本题考查等比数列的通项公式和等比数列的应用,属于较难题目.
设第个图形的边数为,可得为等比数列,求得其通项公式,并求得的通项公式,进而得到和的通项公式,即可对,作出判定;利用等比数列的性质得到,进而求得的最小值,判断C选项;根据的单调性和范围求得单调性和范围,从而求得的最小值,从而判断D选项.
【解析】
由题意可知,下一个图形的边长是上一个图边长的,边数是上一个图形的4倍,
可得周长的递推关系式为,由图知,
,选项A正确;
从第2个图形起,每一个图形的边长均为上一个图形边长的,
所以数列是1为首项, 为公比的等比数列,
所以,选项B错误;
由, 得,
计算得
所以,当且仅当 时取“=”.
因为题中要求,所以选项C错误;
根据选项B中的分析, ,所以
即
设,则在 上单调递增.
所以时,
所以的最小值是.选项D正确.
故选:AD.
11.(多选题)如果有穷数列a1,a2,a3,…,am(m为正整数)满足a1=am,a2=am-1,…,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,
8都是“对称数列”.设{bn}是项数为2m(m>1,m∈N*)的“对称数列”,且1,2,22,23,…,2m-1依次为该数列中连续的前m项,则数列{bn}的前100项和S100可能的取值为( )
A.2100-1 B.251-2
C.226-4 D.2m+1-22m-100-1
【答案】ABD
【分析】
依题意可得数列{bn}为1,2,22,23,…,,,…,23,22,2,1,再对分类讨论,利用等比数列的求和公式计算可得;
【解析】
解:由题意知数列{bn}为1,2,22,23,…,,,…,23,22,2,1.
若,则,故B正确;
若,则,故D正确.
若,则,故A正确.
故选:ABD
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
12.若等比数列的前n项和为,且,则__________.
【答案】5
【分析】
根据题意和等比数列的求和公式,求得,结合求和公式,即可求解.
【解析】
因为,若时,可得,故,
所以,化简得,
整理得,解得或,
因为,解得,所以.
故答案为:.
13.已知数列满足,则的前项和__________.
【答案】
【分析】
根据等比数列前项和的公式求出数列的通项,再利用分组求和法即可求出答案.
【解析】
解:∵,
∴.
故答案为:.
14.在等比数列中,,,记数列的前项和 前项积分别为,,若对任意正整数都成立,则实数的最小值为___________.
【答案】
【分析】
先求出,,再求出,即对任意正整数都成立,求出函数的最大值即得解.
【解析】
因为,,
所以公比,
所以,
所以,,,,要,
即对任意正整数都成立,
只要,
又,
所以或时,取最大值,
所以,的最小值为.
故答案为:8
四、解答题
15.已知等比数列的各项均为正数,成等差数列,且满足,数列的前n项和,且.
(1)求数列和的通项公式;
(2)设,求数列的前n项和.
【答案】
(1)();()
(2)()
【分析】
(1)设等比数列公比q,由给定条件求出q及a1即可得的通项;
由结合“当时,”即可得的通项.
(2)利用(1)的结论分类讨论,借助分组求和方法及等差等比数列求和公式即可计算得解.
(1)
设正项等比数列公比q,因成等差数列,则,即,
,而,解得,又,即,,解得,
所以数列的通项公式是,;
,数列的前n项和,当时,,
整理得:,于是得数列是常数数列,则,得,
所以数列的通项公式是,.
(2)
由(1)知,,
当n为偶数时,
,
当n为奇数时,,
所以数列的前n项和().
【点睛】
思路点睛:给出Sn与an的递推关系,求an,常用思路是:一是转化为an的递推关系,再求其通项公式;二是转化为 Sn的递推关系,先求出Sn与n之间的关系,再求an.
16.科学数据证明,当前严重威胁人类生存与发展的气候变化主要是工业革命以来人类活动造成的二氧化碳排放所致.应对气候变化的关键在于“控碳”,其必由之路是先实现碳达峰,而后实现碳中和.2020年第七十五届联合国大会上,我国向世界郑重承诺力争在2030年前实现碳达峰,努力争取在2060年前实现碳中和.2021年全国两会的政府工作报告明确提出要扎实做好碳达峰和碳中和的各项工作,某地为响应国家号召,大力发展清洁电能,根据规划,2021年度火电发电量为8亿千瓦时,以后每年比上一年减少20%,2021年度清洁电能发电量为4亿千瓦时,以后每年比上一年增长25%.
(1)设从2021年开始的年内火电发电总量为亿千瓦时,清洁电能总发电量为亿千瓦时,求,(约定时为2021年);
(2)从哪一年开始,清洁电能总发电量将会超过火电发电总量?
【答案】
(1);.
(2)2025
【分析】
(1)设2021年起,每年的火力发电量构成数列,每年的清洁电能发电量构成数列,则根据题意得数列是等比数列,公比为,首项为,数列是等比数列,公比为,首项为,再根据等比数列求和即可得答案;
(2)根据题意解即可得答案.
(1)
解:设2021年度火电发电量为亿千瓦时,以后每年度的火力发电量为,
因为根据规划,2021年度以后,火电发电量每年比上一年减少20%,
所以2021年起,每年的火力发电量构成数列,且满足,,
所以数列是等比数列,公比为,首项为,
所以,则,
设2021年度清洁电能发电量为亿千瓦时,以后每年度的清洁电能发电量为,
因为根据规划,2021年度以后清洁电能发电量每年比上一年增长25% ,
所以2021年起,每年的清洁电能发电量构成数列,且满足,,
所以数列是等比数列,公比为,首项为,
所以,则,
(2)
解:根据题意,假设第年清洁电能总发电量将会超过火电发电总量,
所以,即,
整理得,
令,则,即,解得或(舍)
所以,即
故当时,,
即从2025年开始,清洁电能总发电量将会超过火电发电总量
17.已知等差数列满足,
(1)求数列的通项;
(2)无穷等比数列的前n项和为,且,再从条件①、条件②、条件③,这三个条件中选择两个作为已知条件,求满足的最小正整数n.
条件①:;
条件②:;
条件③:.
【答案】
(1);
(2).
【分析】
(1)由等差数列通项公式可构造方程组求得,由此可得;
(2)(i)选择①②时,结合等比数列通项公式和可求得,利用等比数列求和公式求得,由且可解不等式求得结果;
(ii)选择①③时,结合等比数列通项公式和可求得,利用等比数列求和公式求得,由且可解不等式求得结果;
(iii)选择②③时,利用等比数列求和公式和可求得,利用等比数列求和公式求得,由且可解不等式求得结果.
(1)
设等差数列的公差为,则,解得:,
;
(2)
(i)选择①②:
由(1)可知:,,,则.
设等比数列的公比为,,,解得:,
又,,,,
由且得:,则满足的最小正整数;
(ii)选择①③:
由(1)可知:,,,则.
设等比数列的公比为,,,解得:,
又,,解得:,,,
由且得:,则满足的最小正整数;
(iii)选择②③:
由(1)可知:,,,则.
设等比数列的公比为,由得:或.
又,,,,
由且得:,则满足的最小正整数.
21世纪教育网(www.21cnjy.com)
4.3.2.1等比数列的前n项和
要点一 等比数列的前n项和公式
【重点总结】
(1)等比数列前n项和公式分q =1与q≠1两种情况,因此当公比未知时,要对公比进行分类讨论.
(2)q≠1时,公式Sn =与Sn =是等价的,利用an =a1qn -1可以实现它们之间的相互转化.
当已知a1,q与n时,用Sn =较方便;
当已知a1,q与an时,用Sn =较方便.
要点二 等比数列前n项和的性质
(1)当q=1时,=;当q≠±1时,= .
(2)Sn+m=Sm+Sn=Sn+Sm.
(3)设S偶与S奇分别是偶数项的和与奇数项的和.若项数为2n,则=q;若项数为2n+1,则=q.
(4)当q≠-1时,连续m项的和(如Sm,S2m-Sm,S3m-S2m,…)仍组成等比数列(公比为,m≥2),注意:这连续m项的和必须非零才能成立.
【笔记小结】
(1)当q = -1且k为偶数时,Sk,S2k -Sk,S3k -S2k,…不是等比数列;
(2)当q≠ -1时,或q = -1且k为奇数时,Sk,S2k -Sk,S3k -S2k,…是等比数列.
(3)若{an}是公比为q的等比数列,则:①前n项积Tn =aq;②连续m项的积仍为等比数列,即Tm,,,…是等比数列,公比为qm2.
【基础自测】
1.判断正误(正确的画“√”,错误的画“×”)
(1)求等比数列{an}的前n项和时可直接套用公式Sn=来求.( )
(2)若首项为a的数列既是等差数列又是等比数列,则其前n项和为Sn=na.( )
(3)若某数列的前n项和公式为Sn=-aqn+a(a≠0,q≠0且q≠1,n∈N*),则此数列一定是等比数列.( )
(4)若Sn为等比数列的前n项和,则S3,S6,S9成等比数列.( )
【答案】(1)×(2)√(3)√(4)×
2.已知等比数列{an}的首项a1=3,公比q=2,则S5等于( )
A.93 B.-93
C.45 D.-45
【答案】A
【解析】S5===93.故选A.
3.已知等比数列{an}的前n项和为Sn,若S3=1,S6=9,则公比q=________.
【答案】2
【解析】S6-S3=a4+a5+a6=(a1+a2+a3)q3=S3·q3=1×q3=8.∴q=2.
题型一 等比数列前n项和的基本运算
【例1】在等比数列{an}中,
(1)S2=30,S3=155,求Sn;
(2)a1+a3=10,a4+a6=,求S5;
(3)a1+an=66,a2an-1=128,Sn=126,求q.
【解析】(1)由题意知
解得或
从而Sn=×5n+1-或Sn=
(2)法一:由题意知
解得从而S5==.
法二:由(a1+a3)q3=a4+a6,
得q3=,从而q=.
又a1+a3=a1(1+q2)=10,
所以a1=8,从而S5==.
(3)因为a2an-1=a1an=128,
所以a1,an是方程x2-66x+128=0的两根.
从而或
又Sn==126,所以q为2或.
【方法归纳】
(1)在等比数列{an}的五个量a1,q,an,n,Sn中,已知其中的三个量,通过列方程组,就能求出另外两个量,这是方程思想与整体思想在数列中的具体应用.
(2)在解决与前n项和有关的问题时,首先要对公比q=1或q≠1进行判断,若两种情况都有可能,则要分类讨论.
【跟踪训练】在等比数列{an}中,
(1)若a1=,an=16,Sn=11,求n和q;
(2)已知S4=1,S8=17,求an.
【解析】(1)由Sn=得11=,∴q=-2,
又由an=a1qn-1得16=(-2)n-1,∴n=5.
(2)若q=1,则S8=2S4,不合题意,
∴q≠1,∴S4==1,S8==17,
两式相除得=17=1+q4,
∴q=2或q=-2,∴a1=或a1=-,
∴an=·2n-1或-·(-2)n-1.
题型二 等比数列前n项和性质的应用
【例2】等比数列{an}的前n项和为Sn,S2=7,S6=91,则S4为( )
A.28 B.32
C.21 D.28或-21
【解析】∵{an}为等比数列,∴S2,S4-S2,S6-S4也为等比数列,
即7,S4-7,91-S4成等比数列,
∴(S4-7)2=7(91-S4),解得S4=28或S4=-21.
∵S4=a1+a2+a3+a4=a1+a2+a1q2+a2q2
=(a1+a2)(1+q2)=S2(1+q2)>S2,∴S4=28.故选A.
【变式训练1】将本例中“S2=7,S6=91”换为“正数等比数列中Sn=2,S3n=14”,则S4n=________.
【答案】30
【解析】设S2n=x,S4n=y,则2,x-2,14-x,y-14成等比数列,所以
所以或(舍去),所以S4n=30.
【例3】等比数列{an}中,公比q=3,S80=32,则a2+a4+a6+…+a80=________.
【答案】24
【解析】设S1=a2+a4+a6+…+a80,
S2=a1+a3+a5+…+a79.则=q=3,即S1=3S2.
又S1+S2=S80=32,∴S1=32,解得S1=24.
即a2+a4+a6+…+a80=24.
【方法技巧】考虑 =q,及S2n =S奇 +S偶.
【变式探究2】本例中的“q=3,S80=32.”改为“项数为偶数的等比数列,它的偶数项之和是奇数项之和的,又它的首项为,且中间两项的和为”,则等比数列的项数为________.
【答案】12
【解析】设等比数列为{an},项数为2n,一个项数为2n的等比数列中,=q,则q=,
又an和an+1为中间两项,则an+an+1=,即a1qn-1+a1qn=,又a1=,q=,
∴·n-1+·n= ·n-1·= n=6.
∴项数为2n=12.
则此等比数列的项数为12.
【方法归纳】
(1)在涉及奇数项和S奇与偶数项和S偶时,常考虑其差或比进行简化运算.若项数为2n,则=q(S奇≠0);若项数为2n+1,则=q(S偶≠0).
(2)等比数列前n项和为Sn(且Sn≠0),则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn(q≠-1).
题型三 an与Sn关系的应用
【例4】设数列{an}的前n项和为Sn.已知a1=1,a2=2,且an+2=3Sn-Sn+1+3,
(1)证明:an+2=3an;
(2)求Sn.
【解析】(1)证明:由已知,an+2=3Sn-Sn+1+3,
因而对任意n∈N*,n≥2,有
an+1=3Sn-1-Sn+3.
两式相减,得an+2-an+1=3an-an+1,
即an+2=3an,n≥2.
又因为a1=1,a2=2,所以a3=3S1-S2+3=3a1-(a1+a2)+3=3a1.
故对一切n∈N*,an+2=3an.
(2)由(1)知,an≠0,所以=3,
于是数列{a2n-1}是首项a1=1,公比为3的等比数列;数列{a2n}是首项a2=2,公比为3的等比数列.因此a2n-1=3n-1,a2n=2×3n-1.
于是S2n=a1+a2+…+a2n=(a1+a3+…+a2n-1)+(a2+a4+…+a2n)=(1+3+…+3n-1)+2(1+3+…+3n-1)=3(1+3+…+3n-1)=,从而S2n-1=S2n-a2n=-2×3n-1=(5×3n-2-1).
综上所述,Sn=
【方法归纳】
由an=Sn-Sn-1(n≥2),进行转化,得到an+2=3an.
由an+2=3an知{an}是由两个等比数列构成,所以求Sn时要分奇数项与偶数项和,并且要注意对n是奇数和偶数时讨论.
【跟踪训练2】若数列{an}的前n项和Sn=an+,则an=________.
【答案】(-2)n-1
【解析】由an=Sn-Sn-1(n≥2)
得an=-2an-1(n≥2)
∴=-2(n≥2)
又a1=1,∴an=(-2)n-1,
经检验当n=1时,上式也适合,∴an=(-2)n-1.
【易错辨析】忽略对公比q的讨论致误
【例5】已知等比数列{an}中,a1=2,S3=6,a3=________.
【答案】2或8
【解析】若q=1,则S3=3a1=6,符合题意,此时a3=a1=2.
若q≠1时,则 S3===6,
解得q=-2,此时a3=a1q2=2×(-2)2=8.
综上a3的值为2或8.
【易错警示】
1出错原因
忽略了对公比q的讨论,直接使用了等比数列的前n项和公式Sn=,从而漏解致误.
2.纠错心得
解答有关等比数列求和问题时,应考虑公比q两种情况q=1或q≠1,否则容易出错.
一、单选题
1.已知等比数列的前n项和为,若,,则( )
A.-2或3 B.-2 C.3 D.
【答案】C
【分析】
用等比数列的基本量表示出,然后代入条件计算得答案.
【解析】
由题可知,
∵,,,
∴,,
∵,,
∴,
∴,
∴.
故选:C.
2.数列,满足,,,则数列的前10项和为( )
A. B.
C. D.
【答案】B
【分析】
根据题干所给条件写出数列,的通项公式,并写出数列,得知数列是等比数列,再用等比数列的前n项和公式即可.
【解析】
∵数列,满足,,,
∴数列是等差数列,首项是2且公差是2,是等比数列,首项是2且公比是2,
∴数列的通项公式为,
数列的通项公式为,
则数列为,设,则,
∴数列是等比数列,且公比为4,首项为4.
则数列的前10项和为,
即数列的前10项和为.
故选:B.
3.设为等比数列的前项和,已知,,则公比( )
A.3 B.4 C.5 D.6
【答案】B
【分析】
根据题干所给条件列式并联立计算即可.
【解析】
设等比数列的第一项为,则,,
因为,则,得①
因为,则,得②
式子①-②,得,显然,,则.
故选:B.
4.数列中,,对任意,若,则( )
A.2 B.3 C.4 D.5
【答案】C
【分析】
取,可得出数列是等比数列,求得数列的通项公式,利用等比数列求和公式可得出关于的等式,由可求得的值.
【解析】
在等式中,令,可得,,
所以,数列是以为首项,以为公比的等比数列,则,
,
,则,解得.
故选:C.
5.设数列满足,则数列的前n项和为( )
A. B.
C. D.
【答案】C
【分析】
由题得(1), ,(2),两式相减求出即得解.
【解析】
由题得(1),
又 (2),
(2)-(1)得适合.
所以,所以数列是以为首项,以的等比数列,
所以.
故选:C
6.定义表示不超过的最大整数,如,.若数列的通项公式为,则( )
A. B. C. D.
【答案】A
【分析】
由题可得当时,含有个数列中的项,又,再利用错位相减法即求.
【解析】
由题知当时,含有个数列中的项,
又,
所以,
两边同乘以,得,
两式相减,得
,
所以.
故选:.
7.给出命题:若(,,都是与无关的常数)等比数列的前项和,则.在这个命题的逆命题、否命题、逆否命题中,真命题的个数是( )
A. B. C. D.
【答案】C
【分析】
根据公式得到原命题为真,故逆否命题为真,举出反例恒等于得到逆命题和否命题为假,得到答案.
【解析】
因为,所以;
当时,,
由于是等比数列,所以对也适合,
所以,化简得,所以原命题是真命题,
因此逆否命题也是真命题;
反之,当时,满足,但此时恒等于,不可能是等比数列的前项和,所以逆命题是假命题,因此,否命题也是假命题.
故选:C.
8.已知数列的前项和为,且满足,若对于任意的,不等式恒成立,则实数的取值范围为( )
A. B.
C. D.
【答案】A
【分析】
首先根据题意求出,从而得到;再由对于任意的,不等式恒成立,得到不等式在时恒成立,从而得到,通过解不等式组即可求出实数的取值范围.
【解析】
因为,所以时,,
两式相减,得,即,
又时,,所以,
因为也适合,所以.
所以,
因为对于任意的,不等式恒成立,
所以对于任意的,不等式恒成立,
即对于任意的,不等式恒成立,
所以只需,即,解得或.
所以实数的取值范围为.
故选:A.
二、多选题
9.在等比数列中,公比,是数列的前n项和,若,,则下列结论正确的是( )
A. B.
C.数列是等比数列 D.数列是公差为2的等差数列
【答案】BC
【分析】
利用已知结合等比数列的通项公式求公比,进而写出通项公式、前n项和公式,结合各选项判断正误即可.
【解析】
由题设,,即,
由可得:,
∴,,
∴且公差为;且.
综上,A、D错误,B、C正确.
故选:BC
10.分形几何学是一门以不规则几何形态为研究对象的几何学,分形几何具有自身相似性,从它的任何一个局部经过放大,都可以得到一个和整体全等的图形如下图的雪花曲线,将一个边长为的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图(2),如此继续下去,得图(3),记为第个图形的边长,记为第个图形的周长,为的前项和,则下列说法正确的是( )
A.
B.
C.若,为中的不同两项,且,则最小值是
D.若恒成立,则的最小值为
【答案】AD
【分析】
本题考查等比数列的通项公式和等比数列的应用,属于较难题目.
设第个图形的边数为,可得为等比数列,求得其通项公式,并求得的通项公式,进而得到和的通项公式,即可对,作出判定;利用等比数列的性质得到,进而求得的最小值,判断C选项;根据的单调性和范围求得单调性和范围,从而求得的最小值,从而判断D选项.
【解析】
由题意可知,下一个图形的边长是上一个图边长的,边数是上一个图形的4倍,
可得周长的递推关系式为,由图知,
,选项A正确;
从第2个图形起,每一个图形的边长均为上一个图形边长的,
所以数列是1为首项, 为公比的等比数列,
所以,选项B错误;
由, 得,
计算得
所以,当且仅当 时取“=”.
因为题中要求,所以选项C错误;
根据选项B中的分析, ,所以
即
设,则在 上单调递增.
所以时,
所以的最小值是.选项D正确.
故选:AD.
11.(多选题)如果有穷数列a1,a2,a3,…,am(m为正整数)满足a1=am,a2=am-1,…,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,
8都是“对称数列”.设{bn}是项数为2m(m>1,m∈N*)的“对称数列”,且1,2,22,23,…,2m-1依次为该数列中连续的前m项,则数列{bn}的前100项和S100可能的取值为( )
A.2100-1 B.251-2
C.226-4 D.2m+1-22m-100-1
【答案】ABD
【分析】
依题意可得数列{bn}为1,2,22,23,…,,,…,23,22,2,1,再对分类讨论,利用等比数列的求和公式计算可得;
【解析】
解:由题意知数列{bn}为1,2,22,23,…,,,…,23,22,2,1.
若,则,故B正确;
若,则,故D正确.
若,则,故A正确.
故选:ABD
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
12.若等比数列的前n项和为,且,则__________.
【答案】5
【分析】
根据题意和等比数列的求和公式,求得,结合求和公式,即可求解.
【解析】
因为,若时,可得,故,
所以,化简得,
整理得,解得或,
因为,解得,所以.
故答案为:.
13.已知数列满足,则的前项和__________.
【答案】
【分析】
根据等比数列前项和的公式求出数列的通项,再利用分组求和法即可求出答案.
【解析】
解:∵,
∴.
故答案为:.
14.在等比数列中,,,记数列的前项和 前项积分别为,,若对任意正整数都成立,则实数的最小值为___________.
【答案】
【分析】
先求出,,再求出,即对任意正整数都成立,求出函数的最大值即得解.
【解析】
因为,,
所以公比,
所以,
所以,,,,要,
即对任意正整数都成立,
只要,
又,
所以或时,取最大值,
所以,的最小值为.
故答案为:8
四、解答题
15.已知等比数列的各项均为正数,成等差数列,且满足,数列的前n项和,且.
(1)求数列和的通项公式;
(2)设,求数列的前n项和.
【答案】
(1)();()
(2)()
【分析】
(1)设等比数列公比q,由给定条件求出q及a1即可得的通项;
由结合“当时,”即可得的通项.
(2)利用(1)的结论分类讨论,借助分组求和方法及等差等比数列求和公式即可计算得解.
(1)
设正项等比数列公比q,因成等差数列,则,即,
,而,解得,又,即,,解得,
所以数列的通项公式是,;
,数列的前n项和,当时,,
整理得:,于是得数列是常数数列,则,得,
所以数列的通项公式是,.
(2)
由(1)知,,
当n为偶数时,
,
当n为奇数时,,
所以数列的前n项和().
【点睛】
思路点睛:给出Sn与an的递推关系,求an,常用思路是:一是转化为an的递推关系,再求其通项公式;二是转化为 Sn的递推关系,先求出Sn与n之间的关系,再求an.
16.科学数据证明,当前严重威胁人类生存与发展的气候变化主要是工业革命以来人类活动造成的二氧化碳排放所致.应对气候变化的关键在于“控碳”,其必由之路是先实现碳达峰,而后实现碳中和.2020年第七十五届联合国大会上,我国向世界郑重承诺力争在2030年前实现碳达峰,努力争取在2060年前实现碳中和.2021年全国两会的政府工作报告明确提出要扎实做好碳达峰和碳中和的各项工作,某地为响应国家号召,大力发展清洁电能,根据规划,2021年度火电发电量为8亿千瓦时,以后每年比上一年减少20%,2021年度清洁电能发电量为4亿千瓦时,以后每年比上一年增长25%.
(1)设从2021年开始的年内火电发电总量为亿千瓦时,清洁电能总发电量为亿千瓦时,求,(约定时为2021年);
(2)从哪一年开始,清洁电能总发电量将会超过火电发电总量?
【答案】
(1);.
(2)2025
【分析】
(1)设2021年起,每年的火力发电量构成数列,每年的清洁电能发电量构成数列,则根据题意得数列是等比数列,公比为,首项为,数列是等比数列,公比为,首项为,再根据等比数列求和即可得答案;
(2)根据题意解即可得答案.
(1)
解:设2021年度火电发电量为亿千瓦时,以后每年度的火力发电量为,
因为根据规划,2021年度以后,火电发电量每年比上一年减少20%,
所以2021年起,每年的火力发电量构成数列,且满足,,
所以数列是等比数列,公比为,首项为,
所以,则,
设2021年度清洁电能发电量为亿千瓦时,以后每年度的清洁电能发电量为,
因为根据规划,2021年度以后清洁电能发电量每年比上一年增长25% ,
所以2021年起,每年的清洁电能发电量构成数列,且满足,,
所以数列是等比数列,公比为,首项为,
所以,则,
(2)
解:根据题意,假设第年清洁电能总发电量将会超过火电发电总量,
所以,即,
整理得,
令,则,即,解得或(舍)
所以,即
故当时,,
即从2025年开始,清洁电能总发电量将会超过火电发电总量
17.已知等差数列满足,
(1)求数列的通项;
(2)无穷等比数列的前n项和为,且,再从条件①、条件②、条件③,这三个条件中选择两个作为已知条件,求满足的最小正整数n.
条件①:;
条件②:;
条件③:.
【答案】
(1);
(2).
【分析】
(1)由等差数列通项公式可构造方程组求得,由此可得;
(2)(i)选择①②时,结合等比数列通项公式和可求得,利用等比数列求和公式求得,由且可解不等式求得结果;
(ii)选择①③时,结合等比数列通项公式和可求得,利用等比数列求和公式求得,由且可解不等式求得结果;
(iii)选择②③时,利用等比数列求和公式和可求得,利用等比数列求和公式求得,由且可解不等式求得结果.
(1)
设等差数列的公差为,则,解得:,
;
(2)
(i)选择①②:
由(1)可知:,,,则.
设等比数列的公比为,,,解得:,
又,,,,
由且得:,则满足的最小正整数;
(ii)选择①③:
由(1)可知:,,,则.
设等比数列的公比为,,,解得:,
又,,解得:,,,
由且得:,则满足的最小正整数;
(iii)选择②③:
由(1)可知:,,,则.
设等比数列的公比为,由得:或.
又,,,,
由且得:,则满足的最小正整数.
21世纪教育网(www.21cnjy.com)
