2021-2022学年人教版七年级数学上册4.2.2 线段长短的比较与运算 课件(29张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册4.2.2 线段长短的比较与运算 课件(29张) |  | |
| 格式 | zip | ||
| 文件大小 | 416.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 14:50:05 | ||
图片预览






文档简介
(共29张PPT)
人教版 七年级上
4.2.2 线段长短的比较与运算
学习目标
1.会画一条线段等于已知线段,会比较两条线段的大小;
2.通过实例体会两点之间线段最短的性质,并能初步应用;
3.了解两点间的距离、线段的中点以及线段的三等分点的意义。
情境引入
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以上办法.
情境引入
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
160cm
170cm
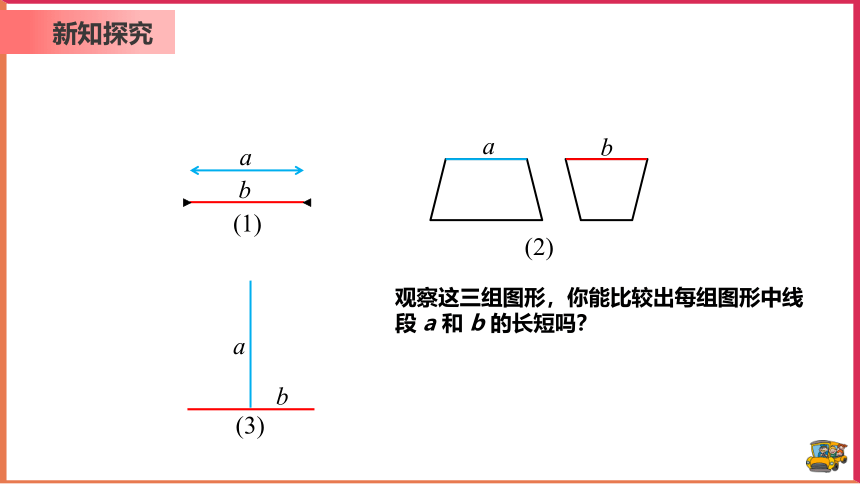
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
(1)
(2)
(3)
a
b
a
a
b
b
新知探究
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
三组图形中,线段a与b的长度均相等
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
(1)
(2)
(3)
a
b
a
a
b
b
新知探究
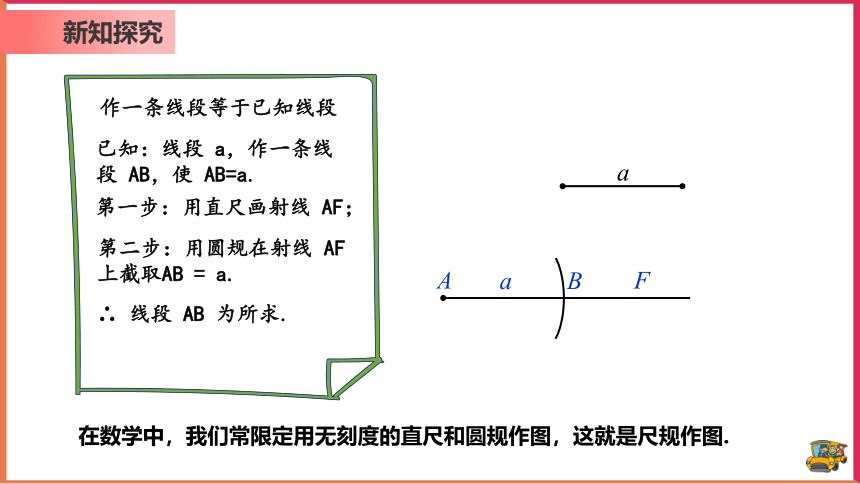
作一条线段等于已知线段
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取AB = a.
∴ 线段 AB 为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
新知探究
叠合法比较两条线段的大小:
AB<CD
什么情况下,AB>CD?
AB=CD呢?
新知探究
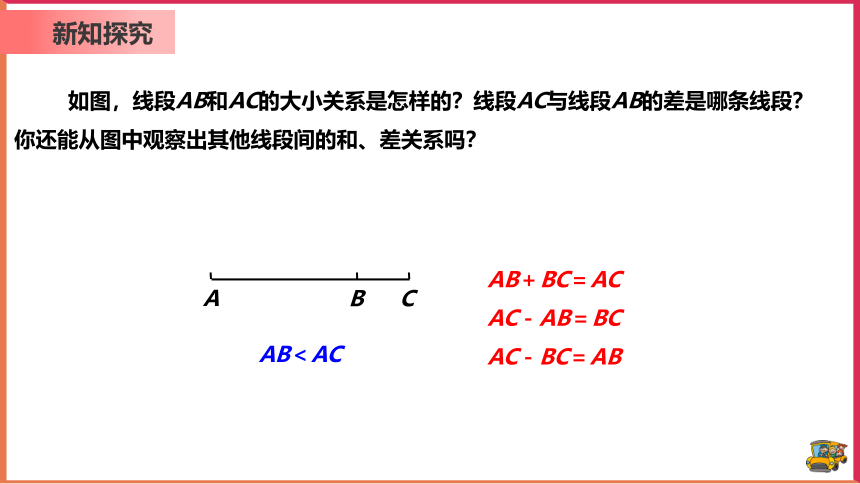
如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗?
A
B
C
AB<AC
AB+BC=AC
AC-AB=BC
AC-BC=AB
新知探究
新知探究
还记得刚开始讨论的对比两位同学身高的方法吗?
160cm
170cm
比较两个同学高矮的方法:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的数值进行比较.
——度量法.
新知探究
如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
CB=a-b
新知探究
符号语言:
∵M是AB的中点
∴AM=BM= AB
如图,已知线段a,求作线段AB=2a.
a
AB=2a
M
B
a
A
P
a
点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点.
想一想:什么是三等分点?四等分点呢?
新知探究
A
B
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
两点的所有连线中,线段最短. 简单地说:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
怎样走最近?
新知探究
过关练习
1.如图,下列关系式中与图不符的是( )
A.AD-CD=AC B. AB+BC=AC
C.BD-BC=AB+BC D. AD-BD=AC-BC
2.如图,点P是线段AB的中点,点Q是线段AP的中点,如果PQ=2 cm,则BQ的长为( )
A.2 cm B.4 cm C.6 cm D.8 cm
C
C
过关练习
3.如图,由A到B有①②③
三条路线,则最短的路线是
_______(填序号),理由是
_________________.
4.下列说法正确的是( )
A.连接两点的线段叫做两点间的距离
B.两点间连线的长度叫做两点间的距离
C.连接两点的直线的长度叫做两点间的距离
D.连接两点的线段的长度叫做两点间的距离
②
两点之间,线段最短
D
过关练习
5.如图,已知点C在线段AB上,线段AC=12,BC=8,点M,N分别是AC,BC的中点,求线段MN的长度;
根据上面的计算过程与结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?用简练的语言表述你发现的规律.
过关练习
5.如图,已知点C在线段AB上,线段AC=12,BC=8,点M,N分别是AC,BC的中点,求线段MN的长度;
根据的计算过程与结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?用简练的语言表述你发现的规律.
要点1 线段长短的比较
比较两条线段的长短.我们可以用刻度尺分别测量出它们的 来比较,即度量法;或用圆规把其中一条线段移到另一条线段上作比较,即叠合法.
要点2 线段的中点
把一条线段分成 的两条线段的点,叫做线段的中点.
要点3 线段的性质
1. 线段的基本事实:两点之间, 最短.
2. 两点的距离是指连接两点间的线段的 .
要点1 长度 要点2 相等 要点3 1. 线段 2. 长度
课堂小结
体验收获
今天我们学习了哪些知识?
1.如何画一条线段等于已知线段?
2.怎样比较两条线段的大小?
3.什么是线段的中点?(三等分点等)
4.关于线段的基本事实是什么?
5.说一说两点的距离的定义?
1. 已知线段AB和线段CD,使端点A与C重合,若点D在线段AB的延长线上,则有( )
A. AB>CD B. AB=CD C. ABC
达标检测
2.A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
C
方法总结:无图时求线段的长,应注意分类讨论,一般分以下两种情况:点在某一线段上;点在该线段的延长线.
达标检测
3. 如果点C是线段AB的中点,那么(1)AB=2AC;(2)2BC=AB;(3)AC=BC;(4)AC+BC=AB,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
D
达标检测
4. 下列四个生活、生产现象:
①在地基上画线时,先在地上钉两根木桩,就可以拉上一条线,沿线用石灰画上白线;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程.
其中可用基本事实“两点之间,线段最短”来解释的现象有( )
A. ①② B. ①③ C. ②④ D. ③④
D
达标检测
5. 如图:AB = 4 cm,BC = 3 cm,如果点O 是线段 AC 的中点.求线段 OB 的长度.
A
B
C
O
解:∵ AC = AB + BC = 4+3=7 (cm),
点O 为线段 AC 的中点,
∴ OC = AC= ×7 = 3.5 (cm),
∴ OB = OC-BC = 3.5-3 = 0.5 (cm).
达标检测
6. 已知线段AB=6cm,试讨论下列问题:
(1)平面内是否存在一点C,使它到A,B两点的距离之和最小?若存在,C点的位置在哪里?最小距离之和是多少?
(2)当点C到A,B两点之间的距离之和大于6cm,C点的位置在什么地方?试举例说明.
(3)由(2)和(3),你能得出一个什么结论?
解:(1)存在点C到A,B两点的距离之和最小,此时,点C应在线段AB上,这个最小的距离之和是6cm.
达标检测
6. 已知线段AB=6cm,试讨论下列问题:
(1)平面内是否存在一点C,使它到A,B两点的距离之和最小?若存在,C点的位置在哪里?最小距离之和是多少?
(2)当点C到A,B两点之间的距离之和大于6cm,C点的位置在什么地方?试举例说明.
(3)由(2)和(3),你能得出一个什么结论?
解: (2)当点C到A,B两点的距离之和大于6cm时,点C的位置在线段外或在其延长线上.例如:如图①,②,③点C分别在线段AB的延长线、反向延长线和线段外,均满足AC+BC>6cm.
达标检测
6. 已知线段AB=6cm,试讨论下列问题:
(1)平面内是否存在一点C,使它到A,B两点的距离之和最小?若存在,C点的位置在哪里?最小距离之和是多少?
(2)当点C到A,B两点之间的距离之和大于6cm,C点的位置在什么地方?试举例说明.
(3)由(2)和(3),你能得出一个什么结论?
(3)平面上,到线段AB两个端点的距离之和最小的点必在线段AB上.
达标检测
作业布置
课后练习册
人教版 七年级上
4.2.2 线段长短的比较与运算
学习目标
1.会画一条线段等于已知线段,会比较两条线段的大小;
2.通过实例体会两点之间线段最短的性质,并能初步应用;
3.了解两点间的距离、线段的中点以及线段的三等分点的意义。
情境引入
做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以上办法.
情境引入
你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
160cm
170cm
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
(1)
(2)
(3)
a
b
a
a
b
b
新知探究
观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗?
三组图形中,线段a与b的长度均相等
很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法.
(1)
(2)
(3)
a
b
a
a
b
b
新知探究
作一条线段等于已知线段
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取AB = a.
∴ 线段 AB 为所求.
a
A F
a
B
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
新知探究
叠合法比较两条线段的大小:
AB<CD
什么情况下,AB>CD?
AB=CD呢?
新知探究
如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗?
A
B
C
AB<AC
AB+BC=AC
AC-AB=BC
AC-BC=AB
新知探究
新知探究
还记得刚开始讨论的对比两位同学身高的方法吗?
160cm
170cm
比较两个同学高矮的方法:
——叠合法.
②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.
①用卷尺分别度量出两个同学的身高,将所得的数值进行比较.
——度量法.
新知探究
如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?
b
a
B
C
a
b
A
P
B
C
a
b
A
P
AC=a+b
CB=a-b
新知探究
符号语言:
∵M是AB的中点
∴AM=BM= AB
如图,已知线段a,求作线段AB=2a.
a
AB=2a
M
B
a
A
P
a
点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点.
想一想:什么是三等分点?四等分点呢?
新知探究
A
B
如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线.
两点的所有连线中,线段最短. 简单地说:两点之间,线段最短.
连接两点间的线段的长度,叫做这两点的距离.
怎样走最近?
新知探究
过关练习
1.如图,下列关系式中与图不符的是( )
A.AD-CD=AC B. AB+BC=AC
C.BD-BC=AB+BC D. AD-BD=AC-BC
2.如图,点P是线段AB的中点,点Q是线段AP的中点,如果PQ=2 cm,则BQ的长为( )
A.2 cm B.4 cm C.6 cm D.8 cm
C
C
过关练习
3.如图,由A到B有①②③
三条路线,则最短的路线是
_______(填序号),理由是
_________________.
4.下列说法正确的是( )
A.连接两点的线段叫做两点间的距离
B.两点间连线的长度叫做两点间的距离
C.连接两点的直线的长度叫做两点间的距离
D.连接两点的线段的长度叫做两点间的距离
②
两点之间,线段最短
D
过关练习
5.如图,已知点C在线段AB上,线段AC=12,BC=8,点M,N分别是AC,BC的中点,求线段MN的长度;
根据上面的计算过程与结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?用简练的语言表述你发现的规律.
过关练习
5.如图,已知点C在线段AB上,线段AC=12,BC=8,点M,N分别是AC,BC的中点,求线段MN的长度;
根据的计算过程与结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?用简练的语言表述你发现的规律.
要点1 线段长短的比较
比较两条线段的长短.我们可以用刻度尺分别测量出它们的 来比较,即度量法;或用圆规把其中一条线段移到另一条线段上作比较,即叠合法.
要点2 线段的中点
把一条线段分成 的两条线段的点,叫做线段的中点.
要点3 线段的性质
1. 线段的基本事实:两点之间, 最短.
2. 两点的距离是指连接两点间的线段的 .
要点1 长度 要点2 相等 要点3 1. 线段 2. 长度
课堂小结
体验收获
今天我们学习了哪些知识?
1.如何画一条线段等于已知线段?
2.怎样比较两条线段的大小?
3.什么是线段的中点?(三等分点等)
4.关于线段的基本事实是什么?
5.说一说两点的距离的定义?
1. 已知线段AB和线段CD,使端点A与C重合,若点D在线段AB的延长线上,则有( )
A. AB>CD B. AB=CD C. AB
达标检测
2.A,B,C三点在同一直线上,线段AB=5cm,BC=4cm,那么A,C两点的距离是( )
A.1cm B.9cm
C.1cm或9cm D.以上答案都不对
C
方法总结:无图时求线段的长,应注意分类讨论,一般分以下两种情况:点在某一线段上;点在该线段的延长线.
达标检测
3. 如果点C是线段AB的中点,那么(1)AB=2AC;(2)2BC=AB;(3)AC=BC;(4)AC+BC=AB,其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
D
达标检测
4. 下列四个生活、生产现象:
①在地基上画线时,先在地上钉两根木桩,就可以拉上一条线,沿线用石灰画上白线;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;
③从A地到B地架设电线,总是尽可能沿着线段AB架设;
④把弯曲的公路改直,就能缩短路程.
其中可用基本事实“两点之间,线段最短”来解释的现象有( )
A. ①② B. ①③ C. ②④ D. ③④
D
达标检测
5. 如图:AB = 4 cm,BC = 3 cm,如果点O 是线段 AC 的中点.求线段 OB 的长度.
A
B
C
O
解:∵ AC = AB + BC = 4+3=7 (cm),
点O 为线段 AC 的中点,
∴ OC = AC= ×7 = 3.5 (cm),
∴ OB = OC-BC = 3.5-3 = 0.5 (cm).
达标检测
6. 已知线段AB=6cm,试讨论下列问题:
(1)平面内是否存在一点C,使它到A,B两点的距离之和最小?若存在,C点的位置在哪里?最小距离之和是多少?
(2)当点C到A,B两点之间的距离之和大于6cm,C点的位置在什么地方?试举例说明.
(3)由(2)和(3),你能得出一个什么结论?
解:(1)存在点C到A,B两点的距离之和最小,此时,点C应在线段AB上,这个最小的距离之和是6cm.
达标检测
6. 已知线段AB=6cm,试讨论下列问题:
(1)平面内是否存在一点C,使它到A,B两点的距离之和最小?若存在,C点的位置在哪里?最小距离之和是多少?
(2)当点C到A,B两点之间的距离之和大于6cm,C点的位置在什么地方?试举例说明.
(3)由(2)和(3),你能得出一个什么结论?
解: (2)当点C到A,B两点的距离之和大于6cm时,点C的位置在线段外或在其延长线上.例如:如图①,②,③点C分别在线段AB的延长线、反向延长线和线段外,均满足AC+BC>6cm.
达标检测
6. 已知线段AB=6cm,试讨论下列问题:
(1)平面内是否存在一点C,使它到A,B两点的距离之和最小?若存在,C点的位置在哪里?最小距离之和是多少?
(2)当点C到A,B两点之间的距离之和大于6cm,C点的位置在什么地方?试举例说明.
(3)由(2)和(3),你能得出一个什么结论?
(3)平面上,到线段AB两个端点的距离之和最小的点必在线段AB上.
达标检测
作业布置
课后练习册
