2021--2022学年人教版七年级数学上册1.5.1 乘方(1)课件(27张)
文档属性
| 名称 | 2021--2022学年人教版七年级数学上册1.5.1 乘方(1)课件(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 17:50:51 | ||
图片预览






文档简介
(共27张PPT)
人教版 七年级上
1.5.1 乘方1
学习目标
1、理解有理数的加、减、乘、除混合运算顺序;正确熟练地进行有理数的混合运算;
2、培养学生解题的良好习惯;
3、在观察、实践的过程中,获得有理数四则混合运算的初步经验。
情境导入一
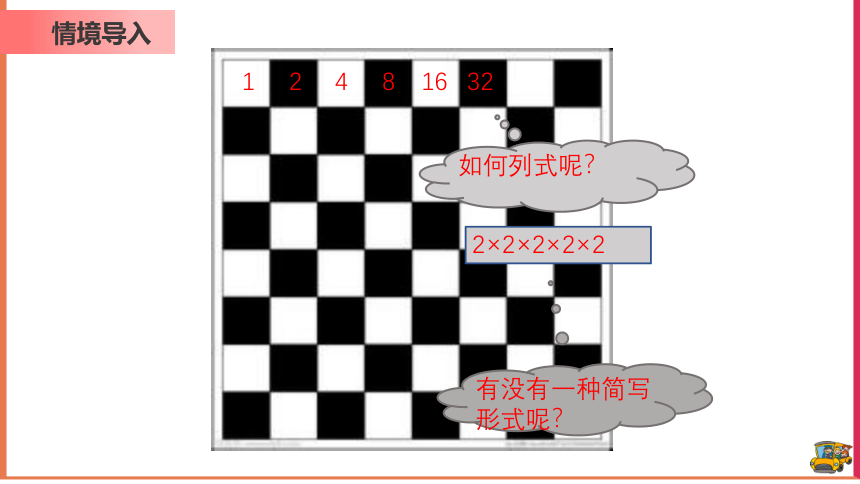
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧,第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒,…,一直到第64格.”“你真傻!就要这么一点米?” 国王哈哈大笑.这位大臣说:“就怕您的国库里没有这么多米!”
棋盘上的学问
情境导入
1
2
4
8
16
如何列式呢?
32
2×2×2×2×2
有没有一种简写形式呢?
情境导入二
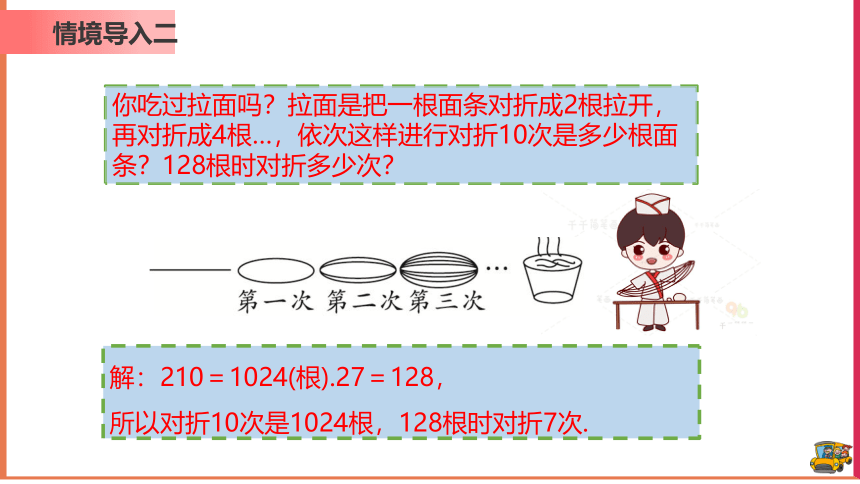
你吃过拉面吗?拉面是把一根面条对折成2根拉开,再对折成4根…,依次这样进行对折10次是多少根面条?128根时对折多少次?
解:210=1024(根).27=128,
所以对折10次是1024根,128根时对折7次.
新知探究1
2×2记作:
边长为2cm的正方形的面积是:____________
列式计算:
2×2=4(cm )
棱长为2cm的正方体的体积是:____________
2×2×2=8(cm )
都是相同因数的乘法,有没有简写形式呢?
2
2×2×2记作:
2
读作:2的平方或2的二次方
读作:2的立方或2的三次方
新知探究1
2×2记作:
2
2×2×2记作:
2
读作:2的平方或2的二次方
读作:2的立方或2的三次方
(-2)×(-2)×(-2)×(-2)记作:
读作:-2的四次方
(-2)4
记作:
读作: 的五次方
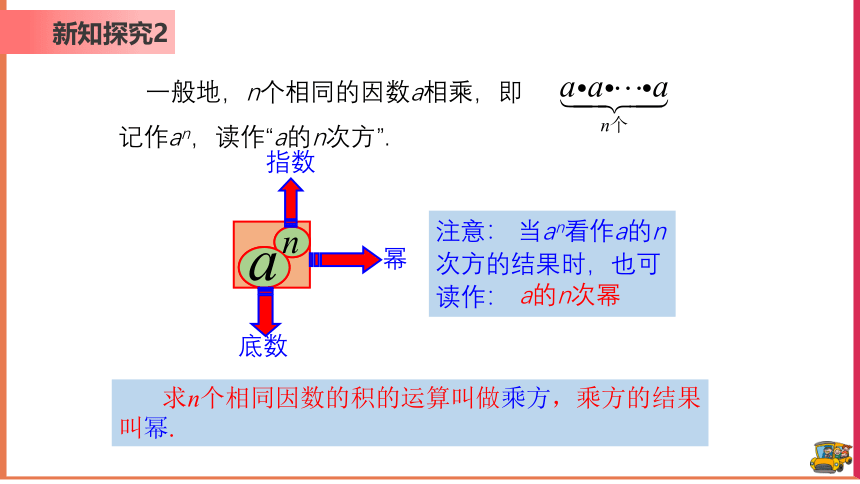
一般地,n个相同的因数a相乘,即
记作an,读作“a的n次方”.
过关练习1
填空:
记作:___________,读作:________________
记作:___________,读作:________________
-24
2的四次方的相反数
想一想:(-2)4与-24一样吗?为什么?
新知探究2
一般地,n个相同的因数a相乘,即
记作an,读作“a的n次方”.
求n个相同因数的积的运算叫做乘方,乘方的结果叫幂.
幂
指数
底数
注意: 当an看作a的n次方的结果时,也可读作:
a的n次幂
过关练习2
填空:
(1)在94中,底数是______, 指数是______,
读作: ______________或_________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(2)在5中,底数是______, 指数是______,
5
1
5=51
指数1通常省略不写
课堂小结
幂
指数
因数的个数
底数
因数
an
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方
乘方的意义
新知探究3
例1 计算:
(1) (-4)3; (2) (-2)4; (3) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
乘方运算转化为乘法运算.
表示3个-4相乘.
过关练习3
计算:
解:
新知探究4
观察:
(-2)4 =16;
(-4)3 =-64;
当指数是______数时,负数的幂是______数;
当指数是______数时,负数的幂是______数.
奇
负
偶
正
课堂小结过关练习4
1.任何一个有理数的偶数次幂( )
A.一定是正数 B.一定是负数
C.一定不是负数 D.一定大于它的绝对值
C
一个数偶次幂总是非负数(正数或0).
如:a2≥0
2.若|x+2|+(y-3)2=0,则 x y 的值为( )
A.8 B.-8 C.9 D.-9
分析:∵ |x+2|≥0,(y-3)2 ≥0
又∵ |x+2|+(y-3)2=0
∴ x+2=0,y-3=0
∴ x =-2,y=3
∴ xy =(-2)3=-8
B
课堂小结
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,
0的任何正整数次幂都是0.
应用提高
1
2
4
8
16
32
26
27
28
29
210
211
212
216=65536
1000粒大米的重在18至23克, 1kg大米约50000粒左右.
213
214
215
216
超过1kg了!
226
226 =67108864
你认为国王的国库里有这么多米吗?
25
……
……
……
超过1t了!
应用提高
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
所以(-8)5=-32768,(-3)6=729.
课堂小结
要点1 有理数的乘方的意义
求n个相同因数的 的运算,叫做乘方.乘方的结果叫做幂.在an中,a叫做 ,n叫做 .当an看作a的运算时,读作“ ”,当an看作a的n次方的结果时,也可读作“ ”.
积
底数
指数
a的n次方
a的n次幂
课堂小结
要点2 有理数乘方的运算
1. 正数的任何次幂都是 ;负数的奇次幂是 .负数的偶次幂是 ;0的任何正整数次幂都是 .
2. 有理数乘方的性质是确定乘方结果的 ,最终的结果还要结合乘方的意义进行计算.
要点3 利用计算器计算有理数的乘方
用计算器计算时,要弄清计算器的每个按键的作用,结合有理数运算的顺序,进行计算.
正数
负数
正数
0
符号
体验收获
今天我们学习了哪些知识?
1.什么是乘方、幂、底数、指数?
2.如何进行有理数的乘方运算?
达标检测
C
B
达标检测
D
C
B
达标测试
6.当n是正整数时,(-1)2n+1-(-1)2n的值是( )
A.2 B.-2 C.0 D.2或-2
7.a是任意有理数,下列说法正确的是( )
A.(a+1)2的值总是正数
B.a2+1的值总是正数
C.-(a+1)2的值总是负数
D.a2+1的值中最大的是1
B
B
达标测试
解:
达标测试
9.规定“☆”是一种运算符号,且a☆b=ab-ba,
例如:2☆3=23-32=8-9=-1,
试计算4☆(3☆2)的值.
4☆(3☆2)=4☆(32-23)
=4☆1
=41-14
=3
解:
所以4☆(3☆2)的值是3.
布置作业
教材47页习题1.4第1题
人教版 七年级上
1.5.1 乘方1
学习目标
1、理解有理数的加、减、乘、除混合运算顺序;正确熟练地进行有理数的混合运算;
2、培养学生解题的良好习惯;
3、在观察、实践的过程中,获得有理数四则混合运算的初步经验。
情境导入一
古时候,有个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋.为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧,第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒,…,一直到第64格.”“你真傻!就要这么一点米?” 国王哈哈大笑.这位大臣说:“就怕您的国库里没有这么多米!”
棋盘上的学问
情境导入
1
2
4
8
16
如何列式呢?
32
2×2×2×2×2
有没有一种简写形式呢?
情境导入二
你吃过拉面吗?拉面是把一根面条对折成2根拉开,再对折成4根…,依次这样进行对折10次是多少根面条?128根时对折多少次?
解:210=1024(根).27=128,
所以对折10次是1024根,128根时对折7次.
新知探究1
2×2记作:
边长为2cm的正方形的面积是:____________
列式计算:
2×2=4(cm )
棱长为2cm的正方体的体积是:____________
2×2×2=8(cm )
都是相同因数的乘法,有没有简写形式呢?
2
2×2×2记作:
2
读作:2的平方或2的二次方
读作:2的立方或2的三次方
新知探究1
2×2记作:
2
2×2×2记作:
2
读作:2的平方或2的二次方
读作:2的立方或2的三次方
(-2)×(-2)×(-2)×(-2)记作:
读作:-2的四次方
(-2)4
记作:
读作: 的五次方
一般地,n个相同的因数a相乘,即
记作an,读作“a的n次方”.
过关练习1
填空:
记作:___________,读作:________________
记作:___________,读作:________________
-24
2的四次方的相反数
想一想:(-2)4与-24一样吗?为什么?
新知探究2
一般地,n个相同的因数a相乘,即
记作an,读作“a的n次方”.
求n个相同因数的积的运算叫做乘方,乘方的结果叫幂.
幂
指数
底数
注意: 当an看作a的n次方的结果时,也可读作:
a的n次幂
过关练习2
填空:
(1)在94中,底数是______, 指数是______,
读作: ______________或_________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(2)在5中,底数是______, 指数是______,
5
1
5=51
指数1通常省略不写
课堂小结
幂
指数
因数的个数
底数
因数
an
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方
乘方的意义
新知探究3
例1 计算:
(1) (-4)3; (2) (-2)4; (3) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
乘方运算转化为乘法运算.
表示3个-4相乘.
过关练习3
计算:
解:
新知探究4
观察:
(-2)4 =16;
(-4)3 =-64;
当指数是______数时,负数的幂是______数;
当指数是______数时,负数的幂是______数.
奇
负
偶
正
课堂小结过关练习4
1.任何一个有理数的偶数次幂( )
A.一定是正数 B.一定是负数
C.一定不是负数 D.一定大于它的绝对值
C
一个数偶次幂总是非负数(正数或0).
如:a2≥0
2.若|x+2|+(y-3)2=0,则 x y 的值为( )
A.8 B.-8 C.9 D.-9
分析:∵ |x+2|≥0,(y-3)2 ≥0
又∵ |x+2|+(y-3)2=0
∴ x+2=0,y-3=0
∴ x =-2,y=3
∴ xy =(-2)3=-8
B
课堂小结
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,
0的任何正整数次幂都是0.
应用提高
1
2
4
8
16
32
26
27
28
29
210
211
212
216=65536
1000粒大米的重在18至23克, 1kg大米约50000粒左右.
213
214
215
216
超过1kg了!
226
226 =67108864
你认为国王的国库里有这么多米吗?
25
……
……
……
超过1t了!
应用提高
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
所以(-8)5=-32768,(-3)6=729.
课堂小结
要点1 有理数的乘方的意义
求n个相同因数的 的运算,叫做乘方.乘方的结果叫做幂.在an中,a叫做 ,n叫做 .当an看作a的运算时,读作“ ”,当an看作a的n次方的结果时,也可读作“ ”.
积
底数
指数
a的n次方
a的n次幂
课堂小结
要点2 有理数乘方的运算
1. 正数的任何次幂都是 ;负数的奇次幂是 .负数的偶次幂是 ;0的任何正整数次幂都是 .
2. 有理数乘方的性质是确定乘方结果的 ,最终的结果还要结合乘方的意义进行计算.
要点3 利用计算器计算有理数的乘方
用计算器计算时,要弄清计算器的每个按键的作用,结合有理数运算的顺序,进行计算.
正数
负数
正数
0
符号
体验收获
今天我们学习了哪些知识?
1.什么是乘方、幂、底数、指数?
2.如何进行有理数的乘方运算?
达标检测
C
B
达标检测
D
C
B
达标测试
6.当n是正整数时,(-1)2n+1-(-1)2n的值是( )
A.2 B.-2 C.0 D.2或-2
7.a是任意有理数,下列说法正确的是( )
A.(a+1)2的值总是正数
B.a2+1的值总是正数
C.-(a+1)2的值总是负数
D.a2+1的值中最大的是1
B
B
达标测试
解:
达标测试
9.规定“☆”是一种运算符号,且a☆b=ab-ba,
例如:2☆3=23-32=8-9=-1,
试计算4☆(3☆2)的值.
4☆(3☆2)=4☆(32-23)
=4☆1
=41-14
=3
解:
所以4☆(3☆2)的值是3.
布置作业
教材47页习题1.4第1题
