华东师大版数学八年级上册 13.5.2线段的垂直平分线 课件(共22张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 13.5.2线段的垂直平分线 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 528.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 23:15:05 | ||
图片预览






文档简介
(共22张PPT)
线段的垂直平分线
张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
单元导入 明确目标
A
B
L
实际问题2
在济青高速公路L(淄博段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
济 青 高 速 公 路
单元导入 明确目标
学习目标:
1.理解线段垂直平分线的性质定理及其逆定理;
2.理解并掌握线段垂直平分线性质定理和逆定理的证明过程;
3.会运用两个定理进行有关证明和计算。
单元导入 明确目标
自学指导 合作探究
PA=PB
P1A=P1B
……
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。这个命题成立吗?
1、动手操作:作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
自主学习:阅读教材P94__95
2、这个命题的逆命题是什么?逆命题成立吗?
P
A
C
N
M
B
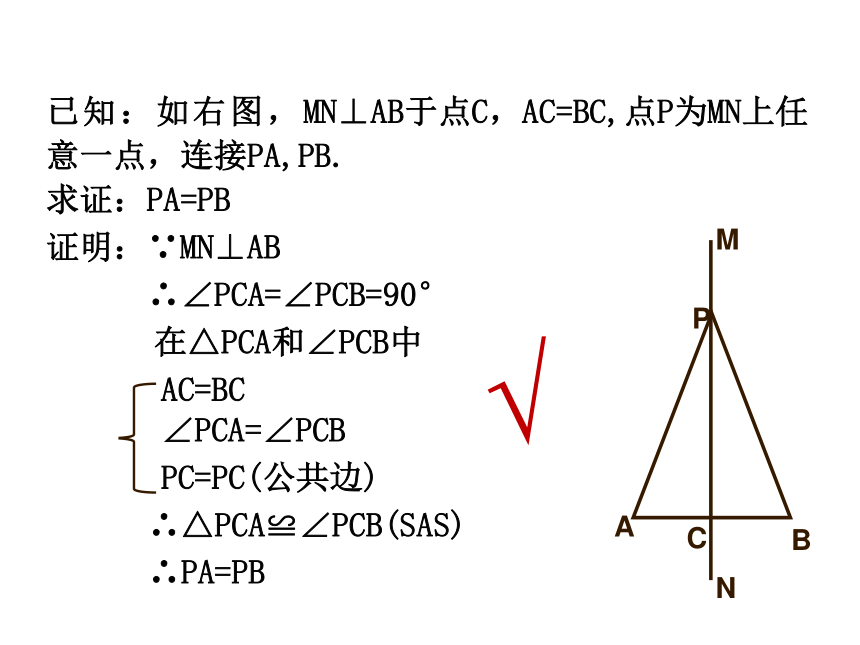
已知:如右图,MN⊥AB于点C,AC=BC,点P为MN上任意一点,连接PA,PB.
求证:PA=PB
∴△PCA≌∠PCB(SAS)
证明:∵MN⊥AB
在△PCA和∠PCB中
∴∠PCA=∠PCB=90°
AC=BC
∠PCA=∠PCB
PC=PC(公共边)
∴PA=PB
√
大组汇报 教师点拨
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等
大组汇报 教师点拨
性质定理的逆命题是什么?
逆命题是否成立?
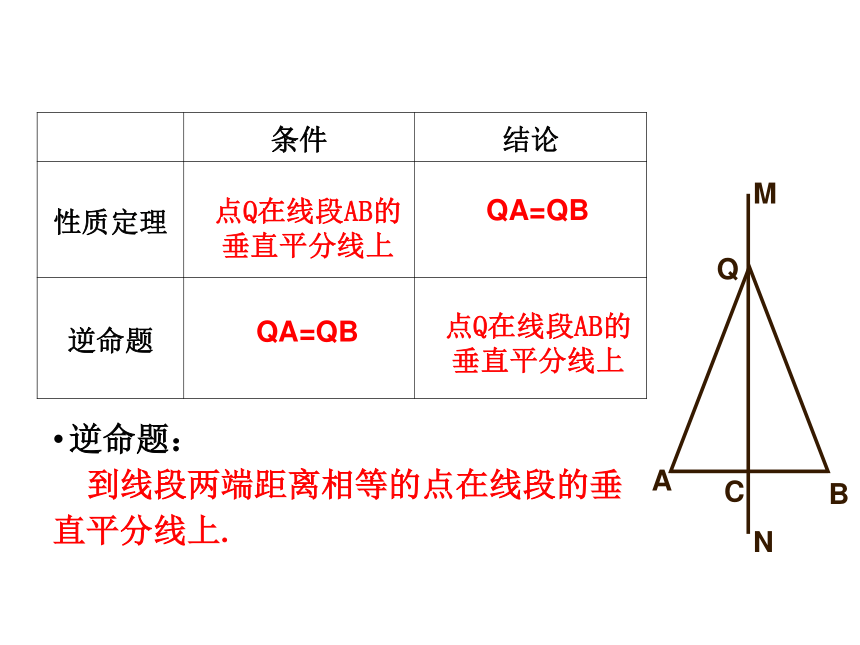
逆命题:
到线段两端距离相等的点在线段的垂
直平分线上.
条件 结论
性质定理
逆命题
点Q在线段AB的垂直平分线上
QA=QB
点Q在线段AB的垂直平分线上
QA=QB
Q
A
C
N
M
B
大组汇报 教师点拨
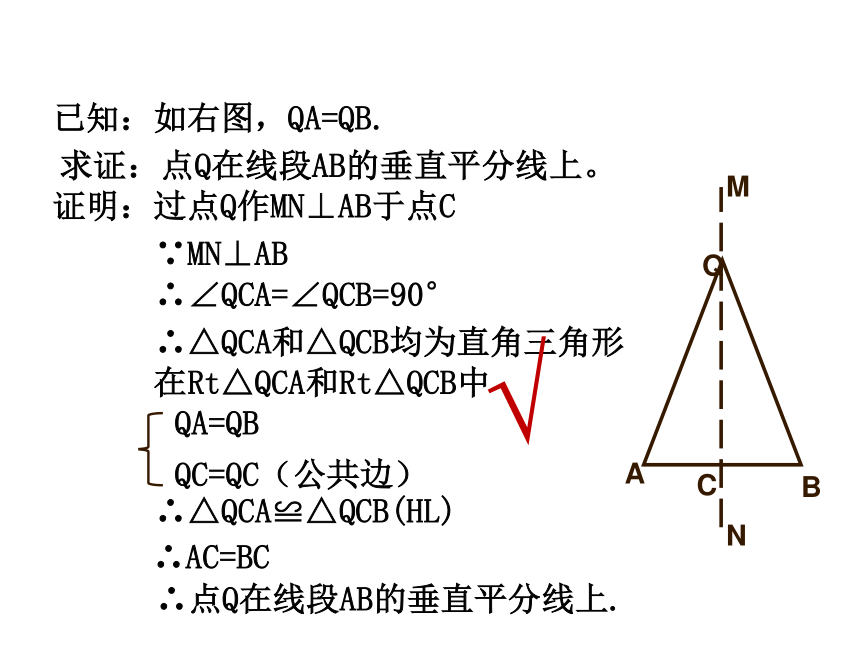
已知:如右图,QA=QB.
求证:点Q在线段AB的垂直平分线上。
Q
A
C
N
M
B
证明:过点Q作MN⊥AB于点C
∵MN⊥AB
∴∠QCA=∠QCB=90°
∴△QCA和△QCB均为直角三角形
在Rt△QCA和Rt△QCB中
QA=QB
QC=QC(公共边)
∴△QCA≌△QCB(HL)
∴AC=BC
∴点Q在线段AB的垂直平分线上.
大组汇报 教师点拨
√
于是得到定理:
到线段两端距离相等的点在线段的垂直平分线上
大组汇报 教师点拨
上述两条定理的关系:互为逆定理
大组汇报 教师点拨
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;
B
A
C
M
N
M’
N’
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。
你能依据例1得到什么结论?
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:PA=PB=PC;
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理 PB=PC.
∴PA=PB=PC.
B
A
C
M
N
M’
N’
P
张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
单元导入 明确目标
B
A
C
巩固练习 拓展提高
1、求作一点P,使它和到△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题1
A
B
L
实际问题2
在济青高速公路L(淄博段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
济 青 高 速 公 路
单元导入 明确目标
巩固练习 拓展提高
2、如图,在直线L上求作一点P,使PA=PB.
L
A
B
实际问题
数学化
实际问题2
p
PA=PB
数学问题源于生活实践,反过来数学又为生活实践服务
1.已知CD为线段AB的垂直平分线,E为直线CD上一点,AE=5cm,∠A=40°,
BE=_______,∠B=_______.
A
B
C
D
E
F
40°
5cm
巩固练习 拓展提高
2.在四边形ABCD中,已知
AB=AD,BC=DC,AC与BD交于点O,
则点A在BD的__________线上,
点C在BD的__________线上,
AC与BD的关系是___________________
A
C
D
B
O
巩固练习 拓展提高
垂直平分
AC为BD的垂直平分线
垂直平分
3.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为24,BC=10,求AB的长。
D
E
A
B
C
分析
因为AB=AC,所以求AB的长即求AC的长,又因为AC=AE+EC,再根据垂直平分线的性质定理和题中的已知条件即可求出
证明:∵DE是AB的垂直平分线
∴EA=EB(垂直平分线的性质定理)
∵△BCE的周长=EB+BC+EC=20,BC=10 ∴EB+EC=20-BC=20-10=10
又∵EA=EB
∴AC=EA+EC
=EB+EC=10
∴AB=10
垂直平分线的性质定理
巩固练习 拓展提高
4.在四边形ABCD中,AB=AD,BC边上的垂直平分线MN经过点A,求证:点A在CD的垂直平分线上
A
C
D
B
M
N
证明:连结AC
∵BC边上的垂直平分线MN经过点A
∴AB=AC(线段垂直平分线的性质定理)
又∵AB=AD
∴AC=AD
∴点A在线段CD的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上)
巩固练习 拓展提高
我们这节课需要重点掌握的两个定理
1.线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等
2.其逆定理:
到线段两端距离相等的点在线段的垂直平分线上
课堂小结 单元回归
线段的垂直平分线
张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
单元导入 明确目标
A
B
L
实际问题2
在济青高速公路L(淄博段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
济 青 高 速 公 路
单元导入 明确目标
学习目标:
1.理解线段垂直平分线的性质定理及其逆定理;
2.理解并掌握线段垂直平分线性质定理和逆定理的证明过程;
3.会运用两个定理进行有关证明和计算。
单元导入 明确目标
自学指导 合作探究
PA=PB
P1A=P1B
……
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。这个命题成立吗?
1、动手操作:作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
自主学习:阅读教材P94__95
2、这个命题的逆命题是什么?逆命题成立吗?
P
A
C
N
M
B
已知:如右图,MN⊥AB于点C,AC=BC,点P为MN上任意一点,连接PA,PB.
求证:PA=PB
∴△PCA≌∠PCB(SAS)
证明:∵MN⊥AB
在△PCA和∠PCB中
∴∠PCA=∠PCB=90°
AC=BC
∠PCA=∠PCB
PC=PC(公共边)
∴PA=PB
√
大组汇报 教师点拨
线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等
大组汇报 教师点拨
性质定理的逆命题是什么?
逆命题是否成立?
逆命题:
到线段两端距离相等的点在线段的垂
直平分线上.
条件 结论
性质定理
逆命题
点Q在线段AB的垂直平分线上
QA=QB
点Q在线段AB的垂直平分线上
QA=QB
Q
A
C
N
M
B
大组汇报 教师点拨
已知:如右图,QA=QB.
求证:点Q在线段AB的垂直平分线上。
Q
A
C
N
M
B
证明:过点Q作MN⊥AB于点C
∵MN⊥AB
∴∠QCA=∠QCB=90°
∴△QCA和△QCB均为直角三角形
在Rt△QCA和Rt△QCB中
QA=QB
QC=QC(公共边)
∴△QCA≌△QCB(HL)
∴AC=BC
∴点Q在线段AB的垂直平分线上.
大组汇报 教师点拨
√
于是得到定理:
到线段两端距离相等的点在线段的垂直平分线上
大组汇报 教师点拨
上述两条定理的关系:互为逆定理
大组汇报 教师点拨
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:PA=PB=PC;
B
A
C
M
N
M’
N’
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
分析:
结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。
你能依据例1得到什么结论?
例1 已知:如图,在ΔABC中,边AB,BC的垂直平分 线交于P.
求证:PA=PB=PC;
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理 PB=PC.
∴PA=PB=PC.
B
A
C
M
N
M’
N’
P
张店区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
实际问题1
单元导入 明确目标
B
A
C
巩固练习 拓展提高
1、求作一点P,使它和到△ABC的三个顶点距离相等.
实际问题
数学化
p
PA=PB=PC
实际问题1
A
B
L
实际问题2
在济青高速公路L(淄博段)的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
济 青 高 速 公 路
单元导入 明确目标
巩固练习 拓展提高
2、如图,在直线L上求作一点P,使PA=PB.
L
A
B
实际问题
数学化
实际问题2
p
PA=PB
数学问题源于生活实践,反过来数学又为生活实践服务
1.已知CD为线段AB的垂直平分线,E为直线CD上一点,AE=5cm,∠A=40°,
BE=_______,∠B=_______.
A
B
C
D
E
F
40°
5cm
巩固练习 拓展提高
2.在四边形ABCD中,已知
AB=AD,BC=DC,AC与BD交于点O,
则点A在BD的__________线上,
点C在BD的__________线上,
AC与BD的关系是___________________
A
C
D
B
O
巩固练习 拓展提高
垂直平分
AC为BD的垂直平分线
垂直平分
3.如图,在△ABC中,AB=AC,DE是AB的垂直平分线,△BCE的周长为24,BC=10,求AB的长。
D
E
A
B
C
分析
因为AB=AC,所以求AB的长即求AC的长,又因为AC=AE+EC,再根据垂直平分线的性质定理和题中的已知条件即可求出
证明:∵DE是AB的垂直平分线
∴EA=EB(垂直平分线的性质定理)
∵△BCE的周长=EB+BC+EC=20,BC=10 ∴EB+EC=20-BC=20-10=10
又∵EA=EB
∴AC=EA+EC
=EB+EC=10
∴AB=10
垂直平分线的性质定理
巩固练习 拓展提高
4.在四边形ABCD中,AB=AD,BC边上的垂直平分线MN经过点A,求证:点A在CD的垂直平分线上
A
C
D
B
M
N
证明:连结AC
∵BC边上的垂直平分线MN经过点A
∴AB=AC(线段垂直平分线的性质定理)
又∵AB=AD
∴AC=AD
∴点A在线段CD的垂直平分线上
(到线段两端距离相等的点在线段的垂直平分线上)
巩固练习 拓展提高
我们这节课需要重点掌握的两个定理
1.线段垂直平分线的性质定理:
线段垂直平分线上的点到线段两端的距离相等
2.其逆定理:
到线段两端距离相等的点在线段的垂直平分线上
课堂小结 单元回归
