人教版初中数学九年级上册 24.1.1 圆 课件(共25张PPT)
文档属性
| 名称 | 人教版初中数学九年级上册 24.1.1 圆 课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 12:09:11 | ||
图片预览








文档简介
(共25张PPT)
24.1.1圆
生活图片欣赏
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于半径.
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
·
r
O
A
固定的端点O叫做圆心
线段OA叫做半径
以点O为圆心的圆,记作“⊙O ”,读作“圆O ”.
圆的定义
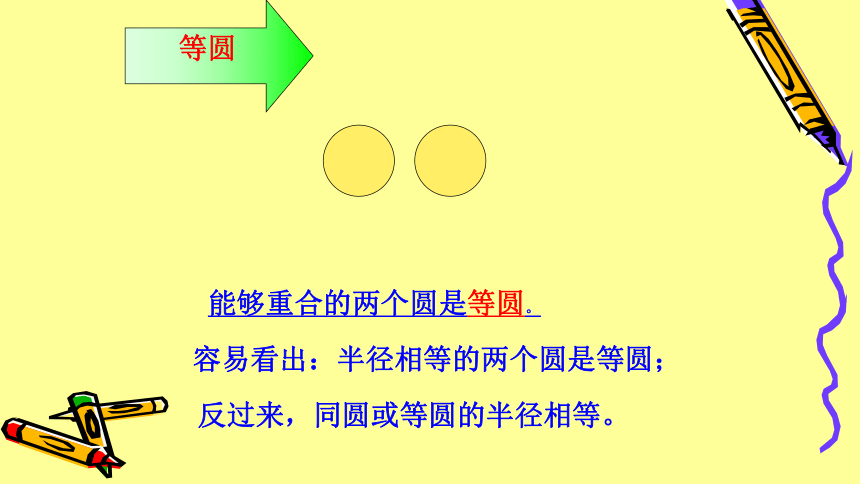
能够重合的两个圆是等圆。
容易看出:半径相等的两个圆是等圆;
反过来,同圆或等圆的半径相等。
等圆
圆心相同半径不同的圆叫做同心圆
同心圆
●
要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
O
(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);
归纳:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形.
从画圆的过程可以看出:
(2)到定点的距离等于定长的点都在同一个圆上.
圆的两种定义
动态:如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形.
根据圆的定义,“圆”指的是“ 圆周 ”,而不是“圆面”。
议一议、说一说
1、车轮为什么做成圆形的?
试想一下,如果车轮不是圆的(比如三角形或正方形),坐车的人会是什么感觉?
议一议、说一说
2、如果车轮做成三角形或正方形的,坐车的人会是什么感觉?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道理。圆上的点到圆心的距离是一个定值
车轮为什么做成圆形的?
归纳总结
·
C
O
A
与圆有关的概念
弦
B
连接圆上任意两点的线段(如图AC)叫做弦,
经过圆心的弦(如图中的AB)叫做直径.
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
O
A
B
⌒
AB
·
B
O
A
弧
大于半圆的弧(用三个字母表示,如图中的 )叫做优弧.
小于半圆的弧(如图中的 )叫做劣弧;
·
C
O
A
B
劣弧与优弧
⌒
⌒
ABC
AC
·
B
O1
A
等弧
在同圆或等圆中,能够互相重合的弧叫做等弧。
·
D
O2
F
E
C
.
O
A
D
Q
C
B
P
H
G
F
E
1、 如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
课堂练习
●
O
B
C
A
2、(1).如图,弧有:_________
⌒
ACB
⌒
BCA
它们一样么?
(2 ).劣弧有:
优弧有:
课堂练习
3、圆中最长的弦长为12cm,则该圆的半径为 。
4、下列说法错误的有( )个
①经过P点的圆有无数个。
②以P为圆心的圆有无数个。
③半径为3cm且经过P点的圆有无数个。
④以P为圆心,以3cm为半径的圆有无数个。
A、1 B、2 C、3 D、4
A
6cm
课堂练习
思考题
已知:矩形ABCD的对角线AC、BD相交于O。
求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴AO=OC;OB=OD;
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为半径的圆上。
例:如图,若AD,BE都是△ABC的高。讨论A、B、D、E四点在同一个圆上吗?
A
A
A
B
C
D
E
O
议一议
课堂小结
1、今天的学习,你有什么收获?
2、圆在生活中运用的道理
2、一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个 怎样安装 请说明理由.
作业
1、同步练习册第一课时
24.1.1圆
生活图片欣赏
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于半径.
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
·
r
O
A
固定的端点O叫做圆心
线段OA叫做半径
以点O为圆心的圆,记作“⊙O ”,读作“圆O ”.
圆的定义
能够重合的两个圆是等圆。
容易看出:半径相等的两个圆是等圆;
反过来,同圆或等圆的半径相等。
等圆
圆心相同半径不同的圆叫做同心圆
同心圆
●
要确定一个圆,必须确定圆的____和____
圆心
半径
圆心确定圆的位置,半径确定圆的大小.
O
(1)圆上各点到定点(圆心O)的距离都等于定长(半径r);
归纳:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形.
从画圆的过程可以看出:
(2)到定点的距离等于定长的点都在同一个圆上.
圆的两种定义
动态:如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
静态:圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r 的点组成的图形.
根据圆的定义,“圆”指的是“ 圆周 ”,而不是“圆面”。
议一议、说一说
1、车轮为什么做成圆形的?
试想一下,如果车轮不是圆的(比如三角形或正方形),坐车的人会是什么感觉?
议一议、说一说
2、如果车轮做成三角形或正方形的,坐车的人会是什么感觉?
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感到非常平稳,这就是车轮都做成圆形的数学道理。圆上的点到圆心的距离是一个定值
车轮为什么做成圆形的?
归纳总结
·
C
O
A
与圆有关的概念
弦
B
连接圆上任意两点的线段(如图AC)叫做弦,
经过圆心的弦(如图中的AB)叫做直径.
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
O
A
B
⌒
AB
·
B
O
A
弧
大于半圆的弧(用三个字母表示,如图中的 )叫做优弧.
小于半圆的弧(如图中的 )叫做劣弧;
·
C
O
A
B
劣弧与优弧
⌒
⌒
ABC
AC
·
B
O1
A
等弧
在同圆或等圆中,能够互相重合的弧叫做等弧。
·
D
O2
F
E
C
.
O
A
D
Q
C
B
P
H
G
F
E
1、 如图(1)直径是_______;
(2)弦是_____________;
(3) PQ是直径吗 ______;
(4)线段EF、GH是弦吗?_______.
K
AB
CD、DK、AB
不是
不是
课堂练习
●
O
B
C
A
2、(1).如图,弧有:_________
⌒
ACB
⌒
BCA
它们一样么?
(2 ).劣弧有:
优弧有:
课堂练习
3、圆中最长的弦长为12cm,则该圆的半径为 。
4、下列说法错误的有( )个
①经过P点的圆有无数个。
②以P为圆心的圆有无数个。
③半径为3cm且经过P点的圆有无数个。
④以P为圆心,以3cm为半径的圆有无数个。
A、1 B、2 C、3 D、4
A
6cm
课堂练习
思考题
已知:矩形ABCD的对角线AC、BD相交于O。
求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴AO=OC;OB=OD;
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为半径的圆上。
例:如图,若AD,BE都是△ABC的高。讨论A、B、D、E四点在同一个圆上吗?
A
A
A
B
C
D
E
O
议一议
课堂小结
1、今天的学习,你有什么收获?
2、圆在生活中运用的道理
2、一个8×10米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个 怎样安装 请说明理由.
作业
1、同步练习册第一课时
同课章节目录
