3.3 对数函数y=logax的图象和性质 题组训练 -2021-2022学年高一上学期数学北师大版(2019)必修第一册 第四章(含答案)
文档属性
| 名称 | 3.3 对数函数y=logax的图象和性质 题组训练 -2021-2022学年高一上学期数学北师大版(2019)必修第一册 第四章(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 10:53:23 | ||
图片预览



文档简介
3.3 对数函数y=logax的图象和性质
基础过关练
题组一 比较函数值的大小
1.下列不等式错误的是( )
A.log0.52.2>log0.52.3 B.log34>log65
C.log310>log520 D.logπe>logeπ
2.设a=log412,b=log515,c=log618,则( )
A.a>b>c B.b>c>a
C.a>c>b D.c>b>a
3.(四川资阳高一月考)设a=60.4,b=log0.40.5,c=log80.4,则a,b,c的大小关系是( )
A.aC.c4.(山东日照高一校际联考)已知a=,b=log2,c=lo,则( )
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
题组二 对数型函数的图象及其应用
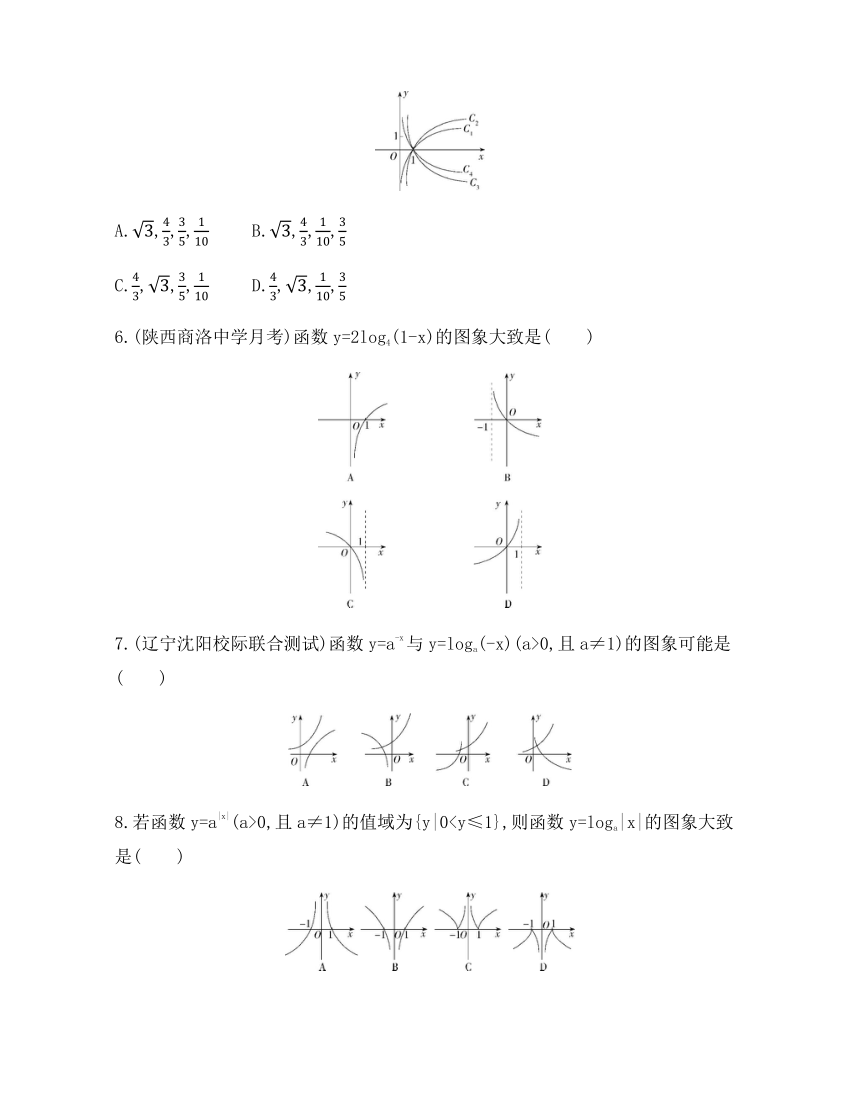
5.(云南大理高一期中)对数函数f(x)=logax的图象如图所示,已知a取,,,,则对应曲线C1,C2,C3,C4的a的值依次为( )
A.,,, B.,,,
C.,,, D.,,,
6.(陕西商洛中学月考)函数y=2log4(1-x)的图象大致是( )
7.(辽宁沈阳校际联合测试)函数y=a-x与y=loga(-x)(a>0,且a≠1)的图象可能是( )
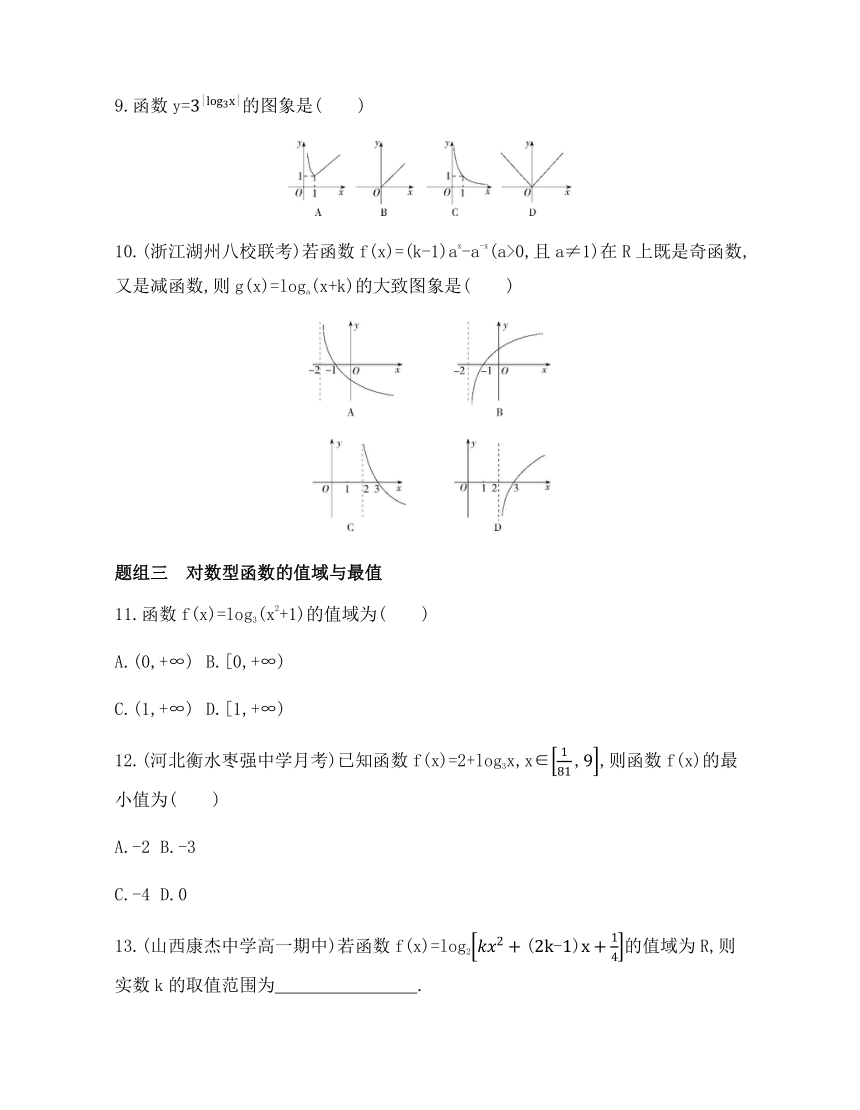
8.若函数y=a|x|(a>0,且a≠1)的值域为{y|09.函数y=的图象是( )
10.(浙江湖州八校联考)若函数f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的大致图象是( )
题组三 对数型函数的值域与最值
11.函数f(x)=log3(x2+1)的值域为( )
A.(0,+∞) B.[0,+∞)
C.(1,+∞) D.[1,+∞)
12.(河北衡水枣强中学月考)已知函数f(x)=2+log3x,x∈,则函数f(x)的最小值为( )
A.-2 B.-3
C.-4 D.0
13.(山西康杰中学高一期中)若函数f(x)=log2的值域为R,则实数k的取值范围为 .
14.(贵州贵阳高一质量检测)设函数f(x)=log2(ax-bx),且f(1)=1,f(2)=log212.
(1)求a,b的值;
(2)当x∈[1,3]时,求f(x)的最大值.
题组四 对数型函数的单调性及其应用
15.(湖南长沙一中高一期中模考)若函数y=loga|x-2|(a>0,且a≠1)在区间(1,2)上是增函数,则f(x)在区间(2,+∞)上( )
A.先增后减 B.先减后增
C.单调递增 D.单调递减
16.若函数f(x)=loga(6-ax)(a>0,且a≠1)在区间[0,2]上为减函数,则a的取值范围是( )
A.(0,1) B.(1,3)
C.(1,3] D.[3,+∞)
17.(江苏南京高一质检)若函数f(x)=对任意x1≠x2,都有<0,则实数a的取值范围是( )
A.(0,1) B.
C. D.
18.已知loga(3a-1)恒为正,则a的取值范围是 .
19.若函数f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上单调递减,则a的取值范围为 .
20.(黑龙江双鸭山一中高一期中)已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是 .
21.求函数y=ln 的单调区间.
22.(辽宁省实验中学高一期中)已知f(x)=lo(x2-ax-a).
(1)当a=-1时,求f(x)的单调区间及值域;
(2)若f(x)在上为增函数,求实数a的取值范围.
题组五 对数不等式
23.若loga(a2+1)A.(0,1) B.
C. D.(0,1)∪(1,+∞)
24.(河北衡水一中模拟)函数f(x)=
若f(a)>f(-a),则实数a的取值范围是( )
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
25.已知函数f(x)=lg(x+1),则不等式026.若f(x)=lg x,g(x)=f(|x|),则当g(lg x)>g(1)时,x的取值范围是 .
27.(河南洛阳高一模拟)已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,f(x)=lox.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
能力提升练
题组一 对数型函数的图象及其应用
1.(河北辛集中学高一期中,)函数y=e|ln x|-|x-1|的图象大致是( )
2.(安徽阜阳太和一中高一上学期期末,)函数f(x)=ln的图象大致为( )
3.(多选)()下列命题中正确的是( )
A.函数f(x)=loga(2x-1)-1(a>0,且a≠1)的图象恒过点(1,-1)
B.函数f(x)=loga|x|(a>0,且a≠1)在(0,+∞)上单调递增,则f(-2)C.若f(x+2)是偶函数,且函数f(x)的图象与x轴有2 017个交点,分别为(x1,0),(x2,0),…,(x2 017,0),则x1+x2+…+x2 017=2 017
D.函数f(x)=lg 的图象关于坐标原点对称
4.(天津塘沽高一模拟,)已知函数y=loga的图象恒过点P,则点P的坐标为 .
题组二 对数型函数的性质及其应用
5.(陕西西安一中高一期中,)已知m=0.95.1,n=5.10.9,p=log0.55.1,则m,n,p的大小关系是( )
A.mC.p6.(山东曲阜实验中学模拟,)已知x∈(e-1,1),a=ln x,b=,c=eln x,则a,b,c的大小关系为( )
A.c>b>a B.b>c>a C.a>b>c D.b>a>c
7.(福建福州高一期中模拟,)已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+f(loa)≤2f(1),则a的取值范围是( )
A.[1,2] B.
C. D.(0,2]
8.(河南平顶山模拟,)函数f(x)=loga|x+1|(a>0,且a≠1),当x∈(-1,0)时,恒有f(x)>0,则( )
A. f(x)在(-∞,0)上是减函数
B. f(x)在(-∞,-1)上是减函数
C. f(x)在(0,+∞)上是增函数
D. f(x)在(-∞,-1)上是增函数
9.(广东东莞高一月考,)若函数f(x)=lo(2x+1)在上恒有f(x)>0,则实数a的取值范围是 .
10.(山东淄博一中月考,)已知函数f(x)=ln(ax2+2x+1).
(1)若f(x)的定义域为R,求实数a的取值范围;
(2)若f(x)的值域为R,求实数a的取值范围.
11.(山东滕州第一中学高一月考,)已知函数f(x)=lg(102x+1)-kx是偶函数.
(1)求k的值;
(2)当a>0时,设g(x)=lg(a·10x-2a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
题组三 对数型函数的综合应用
12.(山东泰安一中期中,)已知函数f(x)=ln(-3x)+1,则
f(lg 2)+f=( )
A.-1 B.0 C.1 D.2
13.(山东青岛高一上期中,)已知函数f(x)=若f(x0)>2,则x0的取值范围是( )
A.-14 B.x0<-1或x0>4
C.014.(吉林白山高一期中,)已知函数y=ex的图象与函数y=f(x)的图象关于直线y=x对称,则( )
A. f(2x)=e2x(x∈R)
B. f(2x)=ln 2·ln x(x>0)
C. f(2x)=2ex(x∈R)
D. f(2x)=ln x+ln 2(x>0)
15.(重庆求精中学高一月考,)函数f(x)=|log2x|,若0A.[4,+∞) B.(4,+∞)
C.[5,+∞) D.(5,+∞)
16.(多选)(广东仲元中学高一期中,)已知函数f(x)=(log2x)2-log2x2-3,则下列说法正确的是( )
A. f(4)=-3
B.函数y=f(x)的图象与x轴有两个交点
C.函数y=f(x)的最小值为-4
D.函数y=f(x)的最大值为4
17.(山东潍坊高一期末,)已知函数f(x)=,函数y=g(x)为函数y=f(x)的反函数.
(1)求函数y=g(x)的解析式;
(2)若方程g(x)=ln[(a-3)x+2a-4]恰有一个实根,求实数a的取值范围;
(3)设a>0,若对任意b∈,当x1,x2∈[b,b+1]时,满足|g(x1)-g(x2)|≤ln 4,求实数a的取值范围.
18.(安徽六安第一中学高三月考,)已知a∈R,函数f(x)=log2.
(1)当a=1时,解不等式f(x)<1;
(2)若函数y=f(x)+1为奇函数,试求a的值;
(3)若关于x的方程f(x+1)-log2[(a-4)x+2a-5]=0的解集中有且只有一个元素,求a的取值范围.
答案全解全析
基础过关练
1.D 函数y=logπx在定义域上单调递增,e<π,则logπelogee=1,所以logπe2.A 易知a=1+log43,b=1+log53,c=1+log63,
∵log43>log53>log63,∴a>b>c.
3.B 因为a=60.4>1,b=log0.40.5∈(0,1),c=log80.4<0,所以a>b>c.故选B.
4.C 因为a=,所以01,所以c>1>a>0>b,即c>a>b.故选C.
5.A 作直线y=1与四个图象分别交于四点,四点的横坐标即为对应对数的底数,从左至右依次增大,可知选A.
6.C 函数y=2log4(1-x)的定义域为(-∞,1),排除A,B;又函数y=2log4(1-x)在定义域内单调递减,排除D.故选C.
7.C 在y=loga(-x)中,易知-x>0,∴x<0,
∴图象只能在y轴的左侧,故排除A、D;当a>1时,y=loga(-x)是减函数,y=a-x=是减函数,故排除B;当08.A ∵函数y=a|x|(a>0,且a≠1)的值域为{y|09.A y==
即y=由解析式可以得出,函数图象先是反比例函数图象的一部分,然后是直线y=x的一部分,观察四个选项,只有A选项符合题意,故选A.
10.A ∵f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上是奇函数,∴f(0)=(k-1)a0-a0=k-2=0,∴k=2.又∵f(x)是减函数,∴0∴g(x)=loga(x+k)的图象是选项A中的图象.
11.B 因为x2+1≥1,且y=log3u在[1,+∞)上单调递增,所以log3(x2+1)≥log31=0,故函数f(x)的值域为[0,+∞).
12.A ∵≤x≤9,∴log3≤log3x≤log39,即-4≤log3x≤2,∴-2≤2+log3x≤4.
∴当x=时, f(x)min=-2.
13.答案 ∪[1,+∞)
解析 设u=kx2+(2k-1)x+的值域为A,y=log2u的定义域为B,易知B=(0,+∞),
当k=0时,u=-x+,A=R,则A∩B=(0,+∞),函数f(x)的值域为R,符合题意;
当k≠0时,依题意得k>0,B A,因此(2k-1)2-4×k×≥0,解得k≤或k≥1,
此时k的取值范围是∪[1,+∞).
综上所述,实数k的取值范围为∪[1,+∞).
14.解析 (1)由得
∴
即∴
(2)由(1)知f(x)=log2(4x-2x),设t=2x,∵x∈[1,3],∴t∈[2,8].
令u=4x-2x=t2-t=-,
∴当t=8,即x=3时,u最大,umax=56,
又y=log2u单调递增,∴当u最大时,y也最大,
故f(x)的最大值为3+log27.
15.D 当116.B 函数由y=logau,u=6-ax复合而成,因为a>0,所以u=6-ax是减函数,因为函数f(x)在[0,2]上为减函数,所以函数y=logau是增函数,所以a>1,因为u=6-ax在[0,2]上为减函数,所以当x=2时,u=6-ax取得最小值,令6-2a>0,解得a<3,所以117.D 由<0得, f(x)在R上是减函数,则有解得≤a<,故选D.
18.答案
解析 由题意知loga(3a-1)>0=loga1恒成立.
当a>1时,y=logax是增函数,
∴解得a>,∴a>1;
当0∴解得综上所述,a的取值范围是a1.
19.答案 [1,2)
解析 令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,图象的对称轴为直线x=a,要使函数在(-∞,1]上单调递减,则有即
解得1≤a<2,即a∈[1,2).
20.答案
解析 当a>1时, f(x)=loga(8-ax)在[1,2]上是减函数,
由f(x)>1恒成立,得f(x)min=loga(8-2a)>1,解得1当0由f(x)>1恒成立,得f(x)min=loga(8-a)>1,即8-2a<0,所以a>4,又0综上,实数a的取值范围是.
21.解析 函数y=ln 的定义域为(1,+∞),在区间(1,+∞)上,函数y=为减函数,
∴函数y=ln 为减函数.
∴函数y=ln 的单调递减区间为(1,+∞),没有单调递增区间.
22.解析 (1)当a=-1时,
f(x)=lo(x2+x+1),
∵x2+x+1=+≥,
∴lo(x2+x+1)≤lo=2-log23,
∴f(x)的值域为(-∞,2-log23].
∵y=x2+x+1在上单调递减,在上单调递增,y=lox在(0,+∞)上单调递减,
∴f(x)的增区间为,减区间为.
(2)令u(x)=x2-ax-a=--a,
∵f(x)在上为单调递增函数,
且y=lou(x)为单调递减函数,
∴u(x)在上为单调递减函数,且u(x)>0在上恒成立.
∴即解得-1≤a≤.
故实数a的取值范围是.
23.C 由题意得a>0且a≠1,故必有a2+1>2a,又loga(a2+1)同时2a>1,所以a>.综上,a∈.
24.C 当a>0时,由f(a)>f(-a)得log2a>lo[-(-a)],即log2a>0,解得a>1;
当a<0时,由f(a)>f(-a)得lo(-a)>log2(-a),即log2(-a)<0,解得0<-a<1,即-125.答案
解析 不等式0即0由得-1由0因为x+1>0,所以x+1<2-2x<10x+10,解得-综上,不等式的解集为.
26.答案 ∪(10,+∞)
解析 当g(lg x)>g(1)时, f(|lg x|)>f(1),由f(x)为增函数得|lg x|>1,从而lg x<-1或lg x>1,解得010.
27.解析 (1)当x<0时,-x>0,则f(-x)=lo(-x).
因为函数f(x)是偶函数,所以f(-x)=f(x).
所以当x<0时, f(x)=lo(-x),
所以函数f(x)的解析式为f(x)=
(2)因为f(4)=lo4=-2, f(x)是偶函数,
所以不等式f(x2-1)>-2可化为f(|x2-1|)>f(4).
又因为函数f(x)在(0,+∞)上是减函数,所以0<|x2-1|<4,
解得-而当x2-1=0时, f(0)=0>-2成立,
所以-即不等式的解集为(-,).
能力提升练
1.D 当x≥1时,ln x≥0,x-1≥0,因此y=eln x-(x-1)=1,排除C;
当00,排除B,故选D.
2.B 易知f(x)的定义域为(-1,0)∪(1,+∞),故选项A和选项D错误;又因为f(x)在定义域内恒为增函数,故选项C错误.故选B.
3.ABD 由得则函数f(x)的图象恒过点(1,-1),因此A正确;依题意得f(x)是偶函数,且a>1,因此f(-2)=f(2)0,解得x>1或x<-1,函数的定义域关于原点对称,且f(-x)=lg=lg=lg=-lg=-f(x),则f(x)是奇函数,图象关于坐标原点对称,因此D正确.故选ABD.
4.答案 (-2,0)
解析 由loga1=0得解得故y=loga的图象恒过点P(-2,0).
5.C ∵0<0.95.1<0.90=1,5.10.9>5.10=1,log0.55.16.B ∵x∈(e-1,1),∴ln x∈(-1,0),∴a∈(-1,0),b∈(1,2),c∈(e-1,1),∴b>c>a,故选B.
7.C ∵f(x)为偶函数,
∴f(loa)=f(-log2a)=f(log2a),
∴原不等式可化为f(log2a)≤f(1).
又f(x)在区间[0,+∞)上单调递增,
∴|log2a|≤1,∴-1≤log2a≤1,
∴≤a≤2.
8.D 由题意得,函数f(x)的图象关于直线x=-1对称,当x∈(-1,0)时,恒有f(x)>0,即|x+1|∈(0,1), f(x)>0,则09.答案 (-,-1)∪(1,)
解析 因为x∈,
所以2x+1∈(0,1),且lo(2x+1)>0,
所以0所以实数a的取值范围是(-,-1)∪(1,).
10.解析 (1)若f(x)的定义域为R,则y=ax2+2x+1的图象恒在x轴的上方,
所以所以a>1.
(2)若f(x)的值域为R,则y=ax2+2x+1的图象一定要与x轴有交点,且能取得y轴正半轴的任一值,所以a=0或所以0≤a≤1.
11.解析 (1)因为f(x)为偶函数,所以f(-x)=f(x),即
lg(10-2x+1)+kx=lg(102x+1)-kx,
∴2kx=lg=lg102x=2x,∴k=1.
(2)由已知得,方程lg(a·10x-2a)=lg(102x+1)-x=lg有且只有一个解,
∴方程a(10x-2)=有且只有一个解,且满足10x>2,
整理得(a-1)102x-2a·10x-1=0,
令t=10x(t>2),则方程(a-1)t2-2at-1=0在(2,+∞)内有且只有一个实根或有两个相等的实根.
当a=1时,t=-,不满足题意,舍去;
当a>1时,设方程对应的二次函数为u(t)=(a-1)t2-2at-1,
函数的图象开口向上,对称轴为直线t=,且>0,u(0)=-1<0,
只需u(2)<0,则方程只有一个大于2的根,
而u(2)=-5<0,即a>1时满足题意;
当0对称轴为直线t=,且<0,u(0)=-1<0,
此时方程无大于2的实根.
综上,实数a的取值范围是a>1.
D 易知函数f(x)的定义域为R, f(x)+f(-x)=ln(-3x)+ln(+3x)+2=ln(1+9x2-9x2)+2=ln 1+2=2,由上式关系知,
f(lg 2)+f=f(lg 2)+f(-lg 2)=2.
13.A 当x0≤0时,f(x0)>2化为>2,
即x0+2>1,解得x0>-1,∴-1当x0>0时,不等式化为log2x0>2,解得x0>4.综上,x0的取值范围是-14,故选A.
14.D 由y=ex得f(x)=ln x,∴f(2x)=ln 2x=ln 2+ln x(x>0).
15.D 因为0所以log2(ba)=1,所以ab=2.所以y=a+2b=a+(0易知y=a+在(0,1)上为减函数,所以y>1+=5,
所以a+2b的取值范围为(5,+∞),故选D.
16.ABC 对于A, f(4)=-log242-3=-3,正确;
对于B,因为f(x)=-2log2x-3,x∈(0,+∞),所以令f(x)=0,得(log2x+1)·(log2x-3)=0,即得log2x=-1或log2x=3,所以x=或x=8,
即f(x)的图象与x轴有两个交点,正确;
对于C,因为f(x)=-4,x∈(0,+∞),所以当log2x=1,即x=2时,
f(x)min=-4,正确;
对于D,由上可知, f(x)没有最大值.故选ABC.
17.解析 (1)因为y=g(x)为函数y=f(x)的反函数,所以x=,
得y=ln,所以g(x)=ln.
(2)由ln=ln[(a-3)x+2a-4]得(a-3)x2+(a-4)x-1=0,
当a=3时,x=-1,经检验,满足题意;
当a=2时,x1=x2=-1,经检验,满足题意;
当a≠2且a≠3时,x1=,x2=-1,x1≠x2,
若x1是原方程的解,则+a>0,即a>.
若x2是原方程的解,则+a>0,即a>1,于是满足题意的a∈.
综上,a的取值范围为∪{2,3}.
(3)不妨令b≤x1则+a>+a,
即函数g(x)=ln在[b,b+1]上为减函数,
所以g(x)max=ln,g(x)min=ln.
因为当x1,x2∈[b,b+1]时,满足|g(x1)-g(x2)|≤ln 4,
故只需ln-ln≤ln 4,
即3ab2+3(a+1)b-1≥0对任意b∈恒成立.
因为a>0,所以函数y=3ab2+3(a+1)b-1≥0在b∈上单调递增,
当b=时,y有最小值,ymin=a+(a+1)-1=-,
由-≥0,得a≥.
故a的取值范围为.
18.解析 (1)当a=1时,log2<1 0<+1<2
∴不等式的解集为{x|x<0或x>2}.
(2)∵函数y=f(x)+1为奇函数,
∴f(-x)+1=-f(x)-1对定义域内的一切x恒成立,
即log2+1=-log2-1,
∴log2+log2=-2,
即log2=-2,
即=,
即x2-(a-1)2+=0对定义域内的一切x恒成立,
则
解得a=.
(3)依题意知log2=log2[(a-4)x+2a-5],
∴+a=(a-4)x+2a-5>0,①
可得(a-4)x2+(a-5)x-1=0,
即(x+1)·[(a-4)x-1]=0.②
当a=4时,方程②的解为x=-1,代入①式,成立;
当a=3时,方程②的解为x=-1,代入①式,成立;
当a≠3且a≠4时,方程②的解为x=-1或,
若x=-1为①的解,则+a=a-1>0,即a>1;
若x=为①的解,则+a=2a-4>0,即a>2,要使①有且仅有一个解,则1综上,若原方程的解集有且只有一个元素,
则a的取值范围为1
基础过关练
题组一 比较函数值的大小
1.下列不等式错误的是( )
A.log0.52.2>log0.52.3 B.log34>log65
C.log310>log520 D.logπe>logeπ
2.设a=log412,b=log515,c=log618,则( )
A.a>b>c B.b>c>a
C.a>c>b D.c>b>a
3.(四川资阳高一月考)设a=60.4,b=log0.40.5,c=log80.4,则a,b,c的大小关系是( )
A.a
A.a>b>c B.a>c>b
C.c>a>b D.c>b>a
题组二 对数型函数的图象及其应用
5.(云南大理高一期中)对数函数f(x)=logax的图象如图所示,已知a取,,,,则对应曲线C1,C2,C3,C4的a的值依次为( )
A.,,, B.,,,
C.,,, D.,,,
6.(陕西商洛中学月考)函数y=2log4(1-x)的图象大致是( )
7.(辽宁沈阳校际联合测试)函数y=a-x与y=loga(-x)(a>0,且a≠1)的图象可能是( )
8.若函数y=a|x|(a>0,且a≠1)的值域为{y|0
10.(浙江湖州八校联考)若函数f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的大致图象是( )
题组三 对数型函数的值域与最值
11.函数f(x)=log3(x2+1)的值域为( )
A.(0,+∞) B.[0,+∞)
C.(1,+∞) D.[1,+∞)
12.(河北衡水枣强中学月考)已知函数f(x)=2+log3x,x∈,则函数f(x)的最小值为( )
A.-2 B.-3
C.-4 D.0
13.(山西康杰中学高一期中)若函数f(x)=log2的值域为R,则实数k的取值范围为 .
14.(贵州贵阳高一质量检测)设函数f(x)=log2(ax-bx),且f(1)=1,f(2)=log212.
(1)求a,b的值;
(2)当x∈[1,3]时,求f(x)的最大值.
题组四 对数型函数的单调性及其应用
15.(湖南长沙一中高一期中模考)若函数y=loga|x-2|(a>0,且a≠1)在区间(1,2)上是增函数,则f(x)在区间(2,+∞)上( )
A.先增后减 B.先减后增
C.单调递增 D.单调递减
16.若函数f(x)=loga(6-ax)(a>0,且a≠1)在区间[0,2]上为减函数,则a的取值范围是( )
A.(0,1) B.(1,3)
C.(1,3] D.[3,+∞)
17.(江苏南京高一质检)若函数f(x)=对任意x1≠x2,都有<0,则实数a的取值范围是( )
A.(0,1) B.
C. D.
18.已知loga(3a-1)恒为正,则a的取值范围是 .
19.若函数f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上单调递减,则a的取值范围为 .
20.(黑龙江双鸭山一中高一期中)已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是 .
21.求函数y=ln 的单调区间.
22.(辽宁省实验中学高一期中)已知f(x)=lo(x2-ax-a).
(1)当a=-1时,求f(x)的单调区间及值域;
(2)若f(x)在上为增函数,求实数a的取值范围.
题组五 对数不等式
23.若loga(a2+1)
C. D.(0,1)∪(1,+∞)
24.(河北衡水一中模拟)函数f(x)=
若f(a)>f(-a),则实数a的取值范围是( )
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
25.已知函数f(x)=lg(x+1),则不等式0
27.(河南洛阳高一模拟)已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,f(x)=lox.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
能力提升练
题组一 对数型函数的图象及其应用
1.(河北辛集中学高一期中,)函数y=e|ln x|-|x-1|的图象大致是( )
2.(安徽阜阳太和一中高一上学期期末,)函数f(x)=ln的图象大致为( )
3.(多选)()下列命题中正确的是( )
A.函数f(x)=loga(2x-1)-1(a>0,且a≠1)的图象恒过点(1,-1)
B.函数f(x)=loga|x|(a>0,且a≠1)在(0,+∞)上单调递增,则f(-2)
D.函数f(x)=lg 的图象关于坐标原点对称
4.(天津塘沽高一模拟,)已知函数y=loga的图象恒过点P,则点P的坐标为 .
题组二 对数型函数的性质及其应用
5.(陕西西安一中高一期中,)已知m=0.95.1,n=5.10.9,p=log0.55.1,则m,n,p的大小关系是( )
A.m
A.c>b>a B.b>c>a C.a>b>c D.b>a>c
7.(福建福州高一期中模拟,)已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log2a)+f(loa)≤2f(1),则a的取值范围是( )
A.[1,2] B.
C. D.(0,2]
8.(河南平顶山模拟,)函数f(x)=loga|x+1|(a>0,且a≠1),当x∈(-1,0)时,恒有f(x)>0,则( )
A. f(x)在(-∞,0)上是减函数
B. f(x)在(-∞,-1)上是减函数
C. f(x)在(0,+∞)上是增函数
D. f(x)在(-∞,-1)上是增函数
9.(广东东莞高一月考,)若函数f(x)=lo(2x+1)在上恒有f(x)>0,则实数a的取值范围是 .
10.(山东淄博一中月考,)已知函数f(x)=ln(ax2+2x+1).
(1)若f(x)的定义域为R,求实数a的取值范围;
(2)若f(x)的值域为R,求实数a的取值范围.
11.(山东滕州第一中学高一月考,)已知函数f(x)=lg(102x+1)-kx是偶函数.
(1)求k的值;
(2)当a>0时,设g(x)=lg(a·10x-2a),若函数f(x)与g(x)的图象有且只有一个公共点,求实数a的取值范围.
题组三 对数型函数的综合应用
12.(山东泰安一中期中,)已知函数f(x)=ln(-3x)+1,则
f(lg 2)+f=( )
A.-1 B.0 C.1 D.2
13.(山东青岛高一上期中,)已知函数f(x)=若f(x0)>2,则x0的取值范围是( )
A.-1
C.0
A. f(2x)=e2x(x∈R)
B. f(2x)=ln 2·ln x(x>0)
C. f(2x)=2ex(x∈R)
D. f(2x)=ln x+ln 2(x>0)
15.(重庆求精中学高一月考,)函数f(x)=|log2x|,若0
C.[5,+∞) D.(5,+∞)
16.(多选)(广东仲元中学高一期中,)已知函数f(x)=(log2x)2-log2x2-3,则下列说法正确的是( )
A. f(4)=-3
B.函数y=f(x)的图象与x轴有两个交点
C.函数y=f(x)的最小值为-4
D.函数y=f(x)的最大值为4
17.(山东潍坊高一期末,)已知函数f(x)=,函数y=g(x)为函数y=f(x)的反函数.
(1)求函数y=g(x)的解析式;
(2)若方程g(x)=ln[(a-3)x+2a-4]恰有一个实根,求实数a的取值范围;
(3)设a>0,若对任意b∈,当x1,x2∈[b,b+1]时,满足|g(x1)-g(x2)|≤ln 4,求实数a的取值范围.
18.(安徽六安第一中学高三月考,)已知a∈R,函数f(x)=log2.
(1)当a=1时,解不等式f(x)<1;
(2)若函数y=f(x)+1为奇函数,试求a的值;
(3)若关于x的方程f(x+1)-log2[(a-4)x+2a-5]=0的解集中有且只有一个元素,求a的取值范围.
答案全解全析
基础过关练
1.D 函数y=logπx在定义域上单调递增,e<π,则logπe
∵log43>log53>log63,∴a>b>c.
3.B 因为a=60.4>1,b=log0.40.5∈(0,1),c=log80.4<0,所以a>b>c.故选B.
4.C 因为a=,所以0
5.A 作直线y=1与四个图象分别交于四点,四点的横坐标即为对应对数的底数,从左至右依次增大,可知选A.
6.C 函数y=2log4(1-x)的定义域为(-∞,1),排除A,B;又函数y=2log4(1-x)在定义域内单调递减,排除D.故选C.
7.C 在y=loga(-x)中,易知-x>0,∴x<0,
∴图象只能在y轴的左侧,故排除A、D;当a>1时,y=loga(-x)是减函数,y=a-x=是减函数,故排除B;当0
即y=由解析式可以得出,函数图象先是反比例函数图象的一部分,然后是直线y=x的一部分,观察四个选项,只有A选项符合题意,故选A.
10.A ∵f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上是奇函数,∴f(0)=(k-1)a0-a0=k-2=0,∴k=2.又∵f(x)是减函数,∴0
11.B 因为x2+1≥1,且y=log3u在[1,+∞)上单调递增,所以log3(x2+1)≥log31=0,故函数f(x)的值域为[0,+∞).
12.A ∵≤x≤9,∴log3≤log3x≤log39,即-4≤log3x≤2,∴-2≤2+log3x≤4.
∴当x=时, f(x)min=-2.
13.答案 ∪[1,+∞)
解析 设u=kx2+(2k-1)x+的值域为A,y=log2u的定义域为B,易知B=(0,+∞),
当k=0时,u=-x+,A=R,则A∩B=(0,+∞),函数f(x)的值域为R,符合题意;
当k≠0时,依题意得k>0,B A,因此(2k-1)2-4×k×≥0,解得k≤或k≥1,
此时k的取值范围是∪[1,+∞).
综上所述,实数k的取值范围为∪[1,+∞).
14.解析 (1)由得
∴
即∴
(2)由(1)知f(x)=log2(4x-2x),设t=2x,∵x∈[1,3],∴t∈[2,8].
令u=4x-2x=t2-t=-,
∴当t=8,即x=3时,u最大,umax=56,
又y=log2u单调递增,∴当u最大时,y也最大,
故f(x)的最大值为3+log27.
15.D 当1
18.答案
解析 由题意知loga(3a-1)>0=loga1恒成立.
当a>1时,y=logax是增函数,
∴解得a>,∴a>1;
当0
19.答案 [1,2)
解析 令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,图象的对称轴为直线x=a,要使函数在(-∞,1]上单调递减,则有即
解得1≤a<2,即a∈[1,2).
20.答案
解析 当a>1时, f(x)=loga(8-ax)在[1,2]上是减函数,
由f(x)>1恒成立,得f(x)min=loga(8-2a)>1,解得1
21.解析 函数y=ln 的定义域为(1,+∞),在区间(1,+∞)上,函数y=为减函数,
∴函数y=ln 为减函数.
∴函数y=ln 的单调递减区间为(1,+∞),没有单调递增区间.
22.解析 (1)当a=-1时,
f(x)=lo(x2+x+1),
∵x2+x+1=+≥,
∴lo(x2+x+1)≤lo=2-log23,
∴f(x)的值域为(-∞,2-log23].
∵y=x2+x+1在上单调递减,在上单调递增,y=lox在(0,+∞)上单调递减,
∴f(x)的增区间为,减区间为.
(2)令u(x)=x2-ax-a=--a,
∵f(x)在上为单调递增函数,
且y=lou(x)为单调递减函数,
∴u(x)在上为单调递减函数,且u(x)>0在上恒成立.
∴即解得-1≤a≤.
故实数a的取值范围是.
23.C 由题意得a>0且a≠1,故必有a2+1>2a,又loga(a2+1)
24.C 当a>0时,由f(a)>f(-a)得log2a>lo[-(-a)],即log2a>0,解得a>1;
当a<0时,由f(a)>f(-a)得lo(-a)>log2(-a),即log2(-a)<0,解得0<-a<1,即-1
解析 不等式0
26.答案 ∪(10,+∞)
解析 当g(lg x)>g(1)时, f(|lg x|)>f(1),由f(x)为增函数得|lg x|>1,从而lg x<-1或lg x>1,解得0
27.解析 (1)当x<0时,-x>0,则f(-x)=lo(-x).
因为函数f(x)是偶函数,所以f(-x)=f(x).
所以当x<0时, f(x)=lo(-x),
所以函数f(x)的解析式为f(x)=
(2)因为f(4)=lo4=-2, f(x)是偶函数,
所以不等式f(x2-1)>-2可化为f(|x2-1|)>f(4).
又因为函数f(x)在(0,+∞)上是减函数,所以0<|x2-1|<4,
解得-
所以-
能力提升练
1.D 当x≥1时,ln x≥0,x-1≥0,因此y=eln x-(x-1)=1,排除C;
当0
2.B 易知f(x)的定义域为(-1,0)∪(1,+∞),故选项A和选项D错误;又因为f(x)在定义域内恒为增函数,故选项C错误.故选B.
3.ABD 由得则函数f(x)的图象恒过点(1,-1),因此A正确;依题意得f(x)是偶函数,且a>1,因此f(-2)=f(2)
4.答案 (-2,0)
解析 由loga1=0得解得故y=loga的图象恒过点P(-2,0).
5.C ∵0<0.95.1<0.90=1,5.10.9>5.10=1,log0.55.1
7.C ∵f(x)为偶函数,
∴f(loa)=f(-log2a)=f(log2a),
∴原不等式可化为f(log2a)≤f(1).
又f(x)在区间[0,+∞)上单调递增,
∴|log2a|≤1,∴-1≤log2a≤1,
∴≤a≤2.
8.D 由题意得,函数f(x)的图象关于直线x=-1对称,当x∈(-1,0)时,恒有f(x)>0,即|x+1|∈(0,1), f(x)>0,则0
解析 因为x∈,
所以2x+1∈(0,1),且lo(2x+1)>0,
所以0
10.解析 (1)若f(x)的定义域为R,则y=ax2+2x+1的图象恒在x轴的上方,
所以所以a>1.
(2)若f(x)的值域为R,则y=ax2+2x+1的图象一定要与x轴有交点,且能取得y轴正半轴的任一值,所以a=0或所以0≤a≤1.
11.解析 (1)因为f(x)为偶函数,所以f(-x)=f(x),即
lg(10-2x+1)+kx=lg(102x+1)-kx,
∴2kx=lg=lg102x=2x,∴k=1.
(2)由已知得,方程lg(a·10x-2a)=lg(102x+1)-x=lg有且只有一个解,
∴方程a(10x-2)=有且只有一个解,且满足10x>2,
整理得(a-1)102x-2a·10x-1=0,
令t=10x(t>2),则方程(a-1)t2-2at-1=0在(2,+∞)内有且只有一个实根或有两个相等的实根.
当a=1时,t=-,不满足题意,舍去;
当a>1时,设方程对应的二次函数为u(t)=(a-1)t2-2at-1,
函数的图象开口向上,对称轴为直线t=,且>0,u(0)=-1<0,
只需u(2)<0,则方程只有一个大于2的根,
而u(2)=-5<0,即a>1时满足题意;
当0
此时方程无大于2的实根.
综上,实数a的取值范围是a>1.
D 易知函数f(x)的定义域为R, f(x)+f(-x)=ln(-3x)+ln(+3x)+2=ln(1+9x2-9x2)+2=ln 1+2=2,由上式关系知,
f(lg 2)+f=f(lg 2)+f(-lg 2)=2.
13.A 当x0≤0时,f(x0)>2化为>2,
即x0+2>1,解得x0>-1,∴-1
14.D 由y=ex得f(x)=ln x,∴f(2x)=ln 2x=ln 2+ln x(x>0).
15.D 因为0
所以a+2b的取值范围为(5,+∞),故选D.
16.ABC 对于A, f(4)=-log242-3=-3,正确;
对于B,因为f(x)=-2log2x-3,x∈(0,+∞),所以令f(x)=0,得(log2x+1)·(log2x-3)=0,即得log2x=-1或log2x=3,所以x=或x=8,
即f(x)的图象与x轴有两个交点,正确;
对于C,因为f(x)=-4,x∈(0,+∞),所以当log2x=1,即x=2时,
f(x)min=-4,正确;
对于D,由上可知, f(x)没有最大值.故选ABC.
17.解析 (1)因为y=g(x)为函数y=f(x)的反函数,所以x=,
得y=ln,所以g(x)=ln.
(2)由ln=ln[(a-3)x+2a-4]得(a-3)x2+(a-4)x-1=0,
当a=3时,x=-1,经检验,满足题意;
当a=2时,x1=x2=-1,经检验,满足题意;
当a≠2且a≠3时,x1=,x2=-1,x1≠x2,
若x1是原方程的解,则+a>0,即a>.
若x2是原方程的解,则+a>0,即a>1,于是满足题意的a∈.
综上,a的取值范围为∪{2,3}.
(3)不妨令b≤x1
即函数g(x)=ln在[b,b+1]上为减函数,
所以g(x)max=ln,g(x)min=ln.
因为当x1,x2∈[b,b+1]时,满足|g(x1)-g(x2)|≤ln 4,
故只需ln-ln≤ln 4,
即3ab2+3(a+1)b-1≥0对任意b∈恒成立.
因为a>0,所以函数y=3ab2+3(a+1)b-1≥0在b∈上单调递增,
当b=时,y有最小值,ymin=a+(a+1)-1=-,
由-≥0,得a≥.
故a的取值范围为.
18.解析 (1)当a=1时,log2<1 0<+1<2
∴不等式的解集为{x|x<0或x>2}.
(2)∵函数y=f(x)+1为奇函数,
∴f(-x)+1=-f(x)-1对定义域内的一切x恒成立,
即log2+1=-log2-1,
∴log2+log2=-2,
即log2=-2,
即=,
即x2-(a-1)2+=0对定义域内的一切x恒成立,
则
解得a=.
(3)依题意知log2=log2[(a-4)x+2a-5],
∴+a=(a-4)x+2a-5>0,①
可得(a-4)x2+(a-5)x-1=0,
即(x+1)·[(a-4)x-1]=0.②
当a=4时,方程②的解为x=-1,代入①式,成立;
当a=3时,方程②的解为x=-1,代入①式,成立;
当a≠3且a≠4时,方程②的解为x=-1或,
若x=-1为①的解,则+a=a-1>0,即a>1;
若x=为①的解,则+a=2a-4>0,即a>2,要使①有且仅有一个解,则1
则a的取值范围为1
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
