八年级数学16.2.3 整数指数幂
文档属性
| 名称 | 八年级数学16.2.3 整数指数幂 |

|
|
| 格式 | zip | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-10 17:02:33 | ||
图片预览




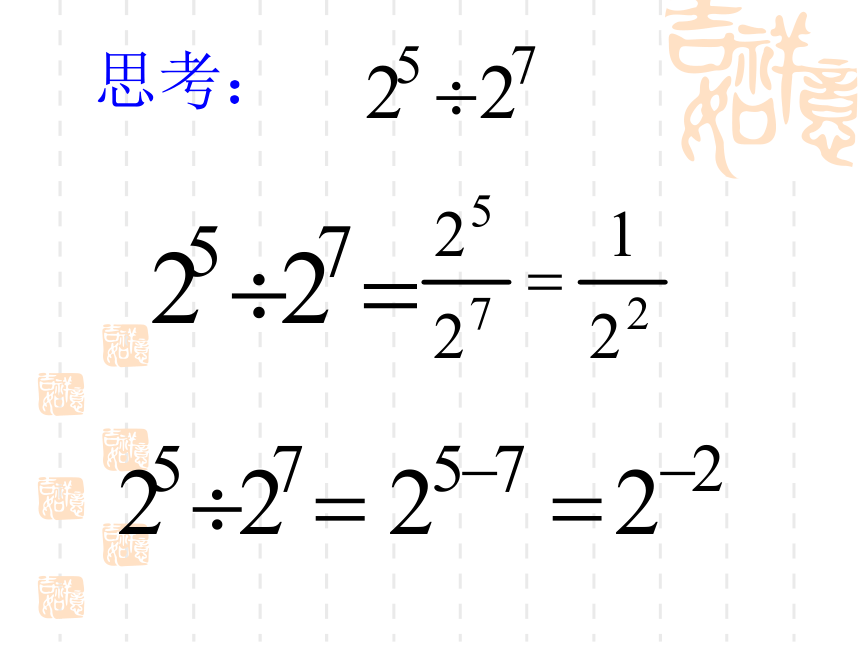
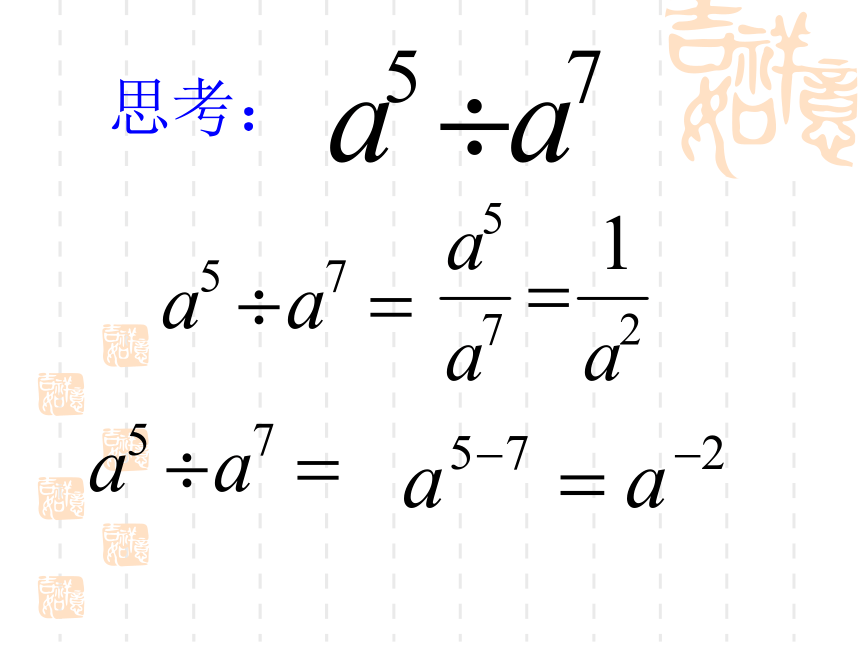

文档简介
(共18张PPT)
复 习
幂的意义是什么?
an=a·a·a········a(n个a相乘)
复习回顾-----幂的有关运算性质
1.同底数幂相乘:
3.积的乘方:
2.幂的乘方:
4.同底数幂相除:
5.分式的乘方:
特别的:
思考:
一般地,
中指数m可以是负整数吗
如果可以,
表示什么
那么负整数指数幂
思考:
思考:
其中a≠0,n是正整数
这就是说:a-n(a≠0)是an 的倒数
例1 填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .
(1)32=_____, 30=___,
3-2=_____;
(2)(-3)2=____,(-3)0=___,
(-3)-2=_____;
练
习
例2、把下列各式转化为只含有正整数指数幂的形式
1、a-3
2、x3y-2
3、2(m+n)-2
4、
5、
6、
正整数指数幂的运算性质是否适合负指数呢?
a-3·a-9=
(a-3)2=
(ab)-3=
a-3÷a-5=
例题:
(1) (a-1b2)3;
(2) a-2b2× (a2b-2)-3
跟踪练习:
(1) x2y-3(x-1y)3;
(2) (2ab2c-3)-2÷(a-2b)3
(对)
(对)
思考:
1、当x为何值时,有意义?
2、当x为何值时,无意义?
3、当x为何值时,值为零?
4、当X为何值时,值为正?
2.已知:10m=5,10n=4,求
102m-3n+1.
复 习
幂的意义是什么?
an=a·a·a········a(n个a相乘)
复习回顾-----幂的有关运算性质
1.同底数幂相乘:
3.积的乘方:
2.幂的乘方:
4.同底数幂相除:
5.分式的乘方:
特别的:
思考:
一般地,
中指数m可以是负整数吗
如果可以,
表示什么
那么负整数指数幂
思考:
思考:
其中a≠0,n是正整数
这就是说:a-n(a≠0)是an 的倒数
例1 填空:
(1) 2-1=___, 3-1=___, x-1=___.
(2) (-2) -1=___, (-3) -1=___, (-x) -1=___.
(3) 4-2=___, (-4) -2=___, -4-2= .
(1)32=_____, 30=___,
3-2=_____;
(2)(-3)2=____,(-3)0=___,
(-3)-2=_____;
练
习
例2、把下列各式转化为只含有正整数指数幂的形式
1、a-3
2、x3y-2
3、2(m+n)-2
4、
5、
6、
正整数指数幂的运算性质是否适合负指数呢?
a-3·a-9=
(a-3)2=
(ab)-3=
a-3÷a-5=
例题:
(1) (a-1b2)3;
(2) a-2b2× (a2b-2)-3
跟踪练习:
(1) x2y-3(x-1y)3;
(2) (2ab2c-3)-2÷(a-2b)3
(对)
(对)
思考:
1、当x为何值时,有意义?
2、当x为何值时,无意义?
3、当x为何值时,值为零?
4、当X为何值时,值为正?
2.已知:10m=5,10n=4,求
102m-3n+1.
