2021-2022学年高一上学期数学苏教版(2019)必修第一册第四讲 函数最值问题辅导讲义
文档属性
| 名称 | 2021-2022学年高一上学期数学苏教版(2019)必修第一册第四讲 函数最值问题辅导讲义 |  | |
| 格式 | docx | ||
| 文件大小 | 513.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 14:36:03 | ||
图片预览




文档简介
第四讲
函数最值问题
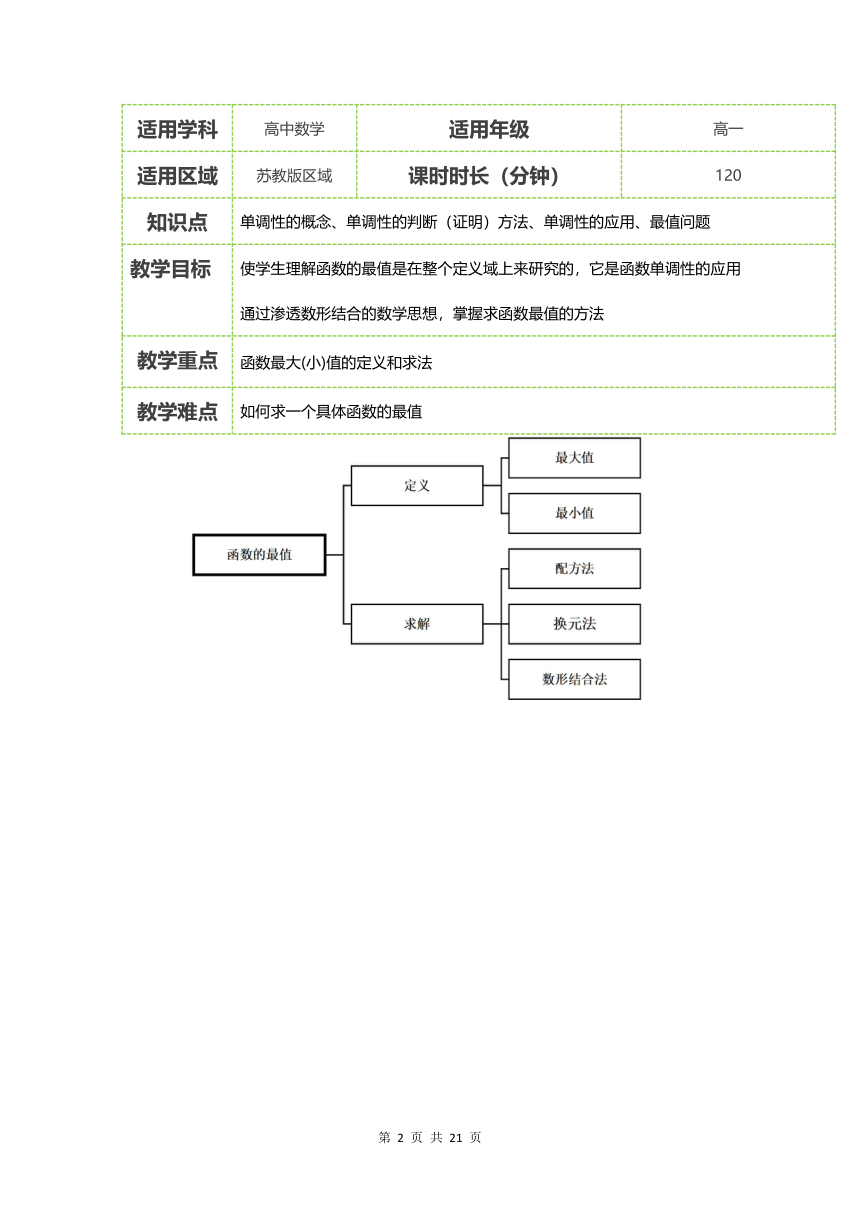
适用学科 高中数学 适用年级 高一
适用区域 苏教版区域 课时时长(分钟) 120
知识点 单调性的概念、单调性的判断(证明)方法、单调性的应用、最值问题
教学目标 使学生理解函数的最值是在整个定义域上来研究的,它是函数单调性的应用 通过渗透数形结合的数学思想,掌握求函数最值的方法
教学重点 函数最大(小)值的定义和求法
教学难点 如何求一个具体函数的最值
教学过程
导入
知识讲解
知识点1 最值的定义
前提 设函数的定义域为,如果存在实数满足
条件 ①对于任意,都有; ②存在,使得 ①对于任意,都有; ②存在,使得
结论 M为最大值 M为最小值
知识点2 函数的最大值
函数图象上任意点的坐标的意义:横坐标是自变量的取值,纵坐标是自变量为时对应的函数值的大小.
(1)图象上最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
(2)由于点C是函数图象上的最高点,则点A在点C的下方,即对定义域内任意,都有,即,也就是对函数的定义域内任意,均有成立.
(3)一般地,设函数的定义域为,如果存在实数满足:
①对于任意的,都有;
②存在,使得.
那么,称是函数的最大值.
(4) 反映了函数的所有函数值不大于实数;这个函数的特征是图象有最高点,并且最高点的纵坐标是.
(5)函数,没有最大值,因为函数,的图象没有最高点.
(6)讨论函数的最大值,要坚持定义域优先的原则;函数图象上有最高点时,这个函数才存在最大值,最高点必须是函数图象上的点.
知识点3 函数的最小值
(1)函数最小值的定义是:
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
①对于任意的x∈I,都有f(x)≥M;
②存在x0∈I,使得f(x0)=M.
那么,称M是函数y=f(x)的最小值。
函数最小值的几何意义:函数图象上最低点的纵坐标.
(2)讨论函数的最小值,也要坚持定义域优先的原则;函数图象上有最低点时,这个函数才存在最小值,最低点必须是函数图象上的点.
三、例题解析
【教学建议】
此处内容主要用于教师课堂的精讲,每个题目结合试题本身、答案和解析部分,教师有的放矢的进行讲授或与学生互动练习。
类型一 单调区间的判断并求最值
例一
画出函数y=-x2+2|x|+3的图象,指出函数的单调区间和最大值.
类型二 通过单调性求函数最值
例二
求函数在区间上的最大值和最小值.
类型三 求抽象函数最值
例三
已知函数对于任意,总有,且当时,, .
(1)求证:在上是减函数;
(2) 求在上的最大值和最小值.
类型四 函数最值的应用
例四
将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
四、课堂运用
基础
1.若函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是________.
2.已知函数y=x+,下列说法正确的是________.(填序号)
①有最小值,无最大值;
②有最大值,无最小值;
③有最小值,最大值2;
④无最大值,也无最小值.
3.已知函数y=x2-2x+3在区间[0,m]上有最大值3,最小值2,则m的取值范围是________.
巩固
4.函数y=-x2+6x+9在区间[a,b](a5.若,则函数的最大值为________.
6.已知,求函数的最值.
7.求函数的最大值.
8.如果函数定义在区间上,求的最小值.
拔高
9.已知函数f(x)=x2-2x+2.
(1)求f(x)在区间上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
10.若二次函数满足f(x+1)-f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上不等式f(x)>2x+m恒成立,求实数m的取值范围.
11. 已知,求的最小值.
12. 已知函数在区间上的最大值为4,求实数的值.
课堂小结
利用单调性求函数的最大(小)值:
(1)定义最大值:设函数的定义域为I,如果存在实数M满足:对于任意的x∈I,都有≤M;存在x0∈I,使得 = M. 那么,称M是函数的最大值(MaximumValue). 仿照最大值定义,可以给出最小值(MinimumValue)的定义.
(2)配方法:研究二次函数的最大(小)值,先配方成后,当时,函数取最小值为;当时,函数取最大值.
(3)单调法:一些函数的单调性,比较容易观察出来,或者可以先证明出函数的单调性,再利用函数的单调性求函数的最大值或最小值.
(4)图象法:先作出其函数图象后,然后观察图象得到函数的最大值或最小值.
五、课后作业
1.如果函数f(x)=x2+bx+c对任意的实数x,都有f(1+x)=f(-x),那么f(-2),f(0), f(2)的大小关系为________.
2.函数y=|x-3|-|x+1|的________.(填序号)
①最小值是0,最大值是4;
②最小值是-4,最大值是0;
③最小值是-4,最大值是4;
④没有最大值也没有最小值.
3.函数的最大值是________.
4. 求函数的最大值.
5. 已知,且,求函数的最值.
6. 已知,当时,求的最大值.
7. 求函数在上的最大值.
8.已知函数f(x)=ax2-|x|+2a-1,其中a≥0,a∈R.
(1)若a=1,作函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.
已知函数在区间上的最小值是最大值是,求,的值.
已知的值域为,求函数的值域.
答案
例一【解析】:函数图象如图所示.
由图象得,函数的图象在区间(-∞,-1)和[0,1]上是上升的,在[-1,0]和(1,+∞)上是下降的,最高点是(±1,4),故函数在(-∞,-1),[0,1]上是增函数;函数在[-1,0],(1,+∞)上是减函数,最大值是4.
例二
【解析】设,则有 .
∵,∴,.
∴,即函数在区间上是减函数.
∴当时,函数在区间上取得最大值;
当时,函数在区间上取得最小值.
例三
【解析】(1)方法一:∵函数对于任意,总有,
令,得.再令,得.在上任取,则,,
又∵时,.而,∴.因此在上是减函数.
方法二:在上任取,,不妨设,
则,
又∵时,,而,
∴,即.
因此在上是减函数.
(2)∵在上为减函数,
∴在上也为减函数,
∴在上的最大值为、最小值为,
而,∵,
∴,
因此,在上的最大值为2,最小值为-2.
例四
答案】为了赚取最大利润,售价应定为70元
【解析】设利润为元,每个售价为元,则每个涨元,从而销售量减少 个,共售出个
∴
∴时,元
四、课堂运用
答案与解析
1.【答案】(-∞,-3]
【解析】由二次函数的性质,可知4≤-(a-1),
解得a≤-3.
2.【答案】①
【解析】∵在定义域上是增函数,
∴,即函数最小值为,无最大值.
3.【答案】[1,2]
【解析】由y=x2-2x+3=(x-1)2+2知,
当x=1时,y的最小值为2,
当y=3时,x2-2x+3=3,解得x=0或x=2.
由y=x2-2x+3的图象知,当m∈[1,2]时,能保证y的最大值为3,最小值为2.
4.【答案】-2 0
【解析】y=-(x-3)2+18,∵a∴函数y在区间[a,b]上单调递增,即-b2+6b+9=9,
得b=0(b=6不合题意,舍去)
-a2+6a+9=-7,得a=-2(a=8不合题意,舍去).
5.【答案】2
【解析】函数在上是单调递增函数,
故.
6.【答案】
【解析】由已知,可得,即函数是定义在区间上的二次函数.将二次函数配方得,其对称轴方程,顶点坐标,且图象开口向上.显然其顶点横坐标不在区间内,如图所示。函数的最小值为,最大值为.
7.【答案】
【解析】令 有,则 ,
8.【答案】
【解析】函数,其对称轴方程为,顶点坐标为,图象开口向上.
如图1所示,若顶点横坐标在区间左侧时,有,此时,当时,函数取得最小值.
图1
如图2所示,若顶点横坐标在区间上时,有,即。当时,函数取得最小值.
图2
如图3所示,若顶点横坐标在区间右侧时,有,即。当时,函数取得最小值.
综上讨论,
图3
9.【答案】同解析
【解析】(1)∵f(x)=x2-2x+2=(x-1)2+1,,
∴f(x)的最小值是f(1)=1,
又, f(3)=5,
所以,f(x)的最大值是f(3)=5,
即f(x)在区间上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2,
∴或,即m≤2或m≥6.
故m的取值范围是(-∞,2]∪[6,+∞).
10.【答案】同解析
【解析】(1)设f(x)=ax2+bx+c(a≠0),由f(0)=1,∴c=1,
∴f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x, ∴2ax+a+b=2x,
∴∴f(x)=x2-x+1.
(2)由题意:x2-x+1>2x+m在[-1,1]上恒成立,
即x2-3x+1-m>0在[-1,1]上恒成立.
令,
其对称轴为,
∴g(x)在区间[-1,1]上是减函数, ∴g(x)min=g(1)=1-3+1-m>0,
∴m<-1.
11.【答案】
【解析】将代入中,得
,即时,
,即时,
所以 .
12.【答案】或
【解析】
(1)若,不符合题意.
(2)若则,由,得.
(3)若时,则,由,得.
综上知或.
课后作业
1.【答案】f(0)【解析】依题意,由f(1+x)=f(-x)知,
二次函数的对称轴为x=,
因为f(x)=x2+bx+c开口向上,
且f(0)=f(1),f(-2)=f(3),
由函数f(x)的图象可知,[,+∞)为f(x)的增区间,
所以f(1)2.【答案】③
【解析】y=|x-3|-|x+1|=.
因为[-1,3)是函数y=-2x+2的减区间,
所以-4≤y≤4,综上可知③正确.
3.【答案】
【解析】
4.【答案】
【解析】令
原函数得最大值为
5.【答案】函数的最小值是,最大值是.
【解析】由已知有,于是函数是定义在区间上的二次函数,将配方得:.
二次函数的对称轴方程是顶点坐标为,图象开口向上
由可得,显然其顶点横坐标在区间的左侧或左端点上.
函数的最小值是,最大值是.
6.【答案】
【解析】:由已知可求对称轴为.
(1)当时,.
(2)当,即时,.
根据对称性,若即时,.
若即时,.
(3)当即时,.
综上,
7.【答案】
【解析】函数图象的对称轴方程为,应分,,即,和这三种情形讨论,下列三图分别为
(1);由图可知
(2);由图可知
(3) 时;由图可知
;即
8.【答案】同解析
【解析】(1)当a=1时,f(x)=x2-|x|+1
=
作图(如右所示)
(2)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,
g(a)=f(2)=-3.
若a>0,则
f(x)图象的对称轴是直线x=.
当0<<1,即a>时,f(x)在区间[1,2]上是增函数,
g(a)=f(1)=3a-2.
当1≤≤2,即≤a≤时,
g(a)==,
当>2,即0g(a)=f(2)=6a-3.
综上可得g(a)=
9.【答案】
【解析】讨论对称轴中 与的位置关系。
①若,则,解得
②若,则,无解
③若,则,无解
④若,则,无解
综上,.
10.【答案】
【解析】令,得.
由于,得.因此.
.
当时有最小值;当时有最大值.
故的值域为.
函数最值问题
适用学科 高中数学 适用年级 高一
适用区域 苏教版区域 课时时长(分钟) 120
知识点 单调性的概念、单调性的判断(证明)方法、单调性的应用、最值问题
教学目标 使学生理解函数的最值是在整个定义域上来研究的,它是函数单调性的应用 通过渗透数形结合的数学思想,掌握求函数最值的方法
教学重点 函数最大(小)值的定义和求法
教学难点 如何求一个具体函数的最值
教学过程
导入
知识讲解
知识点1 最值的定义
前提 设函数的定义域为,如果存在实数满足
条件 ①对于任意,都有; ②存在,使得 ①对于任意,都有; ②存在,使得
结论 M为最大值 M为最小值
知识点2 函数的最大值
函数图象上任意点的坐标的意义:横坐标是自变量的取值,纵坐标是自变量为时对应的函数值的大小.
(1)图象上最高点的纵坐标是所有函数值中的最大值,即函数的最大值.
(2)由于点C是函数图象上的最高点,则点A在点C的下方,即对定义域内任意,都有,即,也就是对函数的定义域内任意,均有成立.
(3)一般地,设函数的定义域为,如果存在实数满足:
①对于任意的,都有;
②存在,使得.
那么,称是函数的最大值.
(4) 反映了函数的所有函数值不大于实数;这个函数的特征是图象有最高点,并且最高点的纵坐标是.
(5)函数,没有最大值,因为函数,的图象没有最高点.
(6)讨论函数的最大值,要坚持定义域优先的原则;函数图象上有最高点时,这个函数才存在最大值,最高点必须是函数图象上的点.
知识点3 函数的最小值
(1)函数最小值的定义是:
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
①对于任意的x∈I,都有f(x)≥M;
②存在x0∈I,使得f(x0)=M.
那么,称M是函数y=f(x)的最小值。
函数最小值的几何意义:函数图象上最低点的纵坐标.
(2)讨论函数的最小值,也要坚持定义域优先的原则;函数图象上有最低点时,这个函数才存在最小值,最低点必须是函数图象上的点.
三、例题解析
【教学建议】
此处内容主要用于教师课堂的精讲,每个题目结合试题本身、答案和解析部分,教师有的放矢的进行讲授或与学生互动练习。
类型一 单调区间的判断并求最值
例一
画出函数y=-x2+2|x|+3的图象,指出函数的单调区间和最大值.
类型二 通过单调性求函数最值
例二
求函数在区间上的最大值和最小值.
类型三 求抽象函数最值
例三
已知函数对于任意,总有,且当时,, .
(1)求证:在上是减函数;
(2) 求在上的最大值和最小值.
类型四 函数最值的应用
例四
将进货单价40元的商品按50元一个售出时,能卖出500个,若此商品每个涨价1元,其销售量减少10个,为了赚到最大利润,售价应定为多少?
四、课堂运用
基础
1.若函数f(x)=x2+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是________.
2.已知函数y=x+,下列说法正确的是________.(填序号)
①有最小值,无最大值;
②有最大值,无最小值;
③有最小值,最大值2;
④无最大值,也无最小值.
3.已知函数y=x2-2x+3在区间[0,m]上有最大值3,最小值2,则m的取值范围是________.
巩固
4.函数y=-x2+6x+9在区间[a,b](a
6.已知,求函数的最值.
7.求函数的最大值.
8.如果函数定义在区间上,求的最小值.
拔高
9.已知函数f(x)=x2-2x+2.
(1)求f(x)在区间上的最大值和最小值;
(2)若g(x)=f(x)-mx在[2,4]上是单调函数,求m的取值范围.
10.若二次函数满足f(x+1)-f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上不等式f(x)>2x+m恒成立,求实数m的取值范围.
11. 已知,求的最小值.
12. 已知函数在区间上的最大值为4,求实数的值.
课堂小结
利用单调性求函数的最大(小)值:
(1)定义最大值:设函数的定义域为I,如果存在实数M满足:对于任意的x∈I,都有≤M;存在x0∈I,使得 = M. 那么,称M是函数的最大值(MaximumValue). 仿照最大值定义,可以给出最小值(MinimumValue)的定义.
(2)配方法:研究二次函数的最大(小)值,先配方成后,当时,函数取最小值为;当时,函数取最大值.
(3)单调法:一些函数的单调性,比较容易观察出来,或者可以先证明出函数的单调性,再利用函数的单调性求函数的最大值或最小值.
(4)图象法:先作出其函数图象后,然后观察图象得到函数的最大值或最小值.
五、课后作业
1.如果函数f(x)=x2+bx+c对任意的实数x,都有f(1+x)=f(-x),那么f(-2),f(0), f(2)的大小关系为________.
2.函数y=|x-3|-|x+1|的________.(填序号)
①最小值是0,最大值是4;
②最小值是-4,最大值是0;
③最小值是-4,最大值是4;
④没有最大值也没有最小值.
3.函数的最大值是________.
4. 求函数的最大值.
5. 已知,且,求函数的最值.
6. 已知,当时,求的最大值.
7. 求函数在上的最大值.
8.已知函数f(x)=ax2-|x|+2a-1,其中a≥0,a∈R.
(1)若a=1,作函数f(x)的图象;
(2)设f(x)在区间[1,2]上的最小值为g(a),求g(a)的表达式.
已知函数在区间上的最小值是最大值是,求,的值.
已知的值域为,求函数的值域.
答案
例一【解析】:函数图象如图所示.
由图象得,函数的图象在区间(-∞,-1)和[0,1]上是上升的,在[-1,0]和(1,+∞)上是下降的,最高点是(±1,4),故函数在(-∞,-1),[0,1]上是增函数;函数在[-1,0],(1,+∞)上是减函数,最大值是4.
例二
【解析】设,则有 .
∵,∴,.
∴,即函数在区间上是减函数.
∴当时,函数在区间上取得最大值;
当时,函数在区间上取得最小值.
例三
【解析】(1)方法一:∵函数对于任意,总有,
令,得.再令,得.在上任取,则,,
又∵时,.而,∴.因此在上是减函数.
方法二:在上任取,,不妨设,
则,
又∵时,,而,
∴,即.
因此在上是减函数.
(2)∵在上为减函数,
∴在上也为减函数,
∴在上的最大值为、最小值为,
而,∵,
∴,
因此,在上的最大值为2,最小值为-2.
例四
答案】为了赚取最大利润,售价应定为70元
【解析】设利润为元,每个售价为元,则每个涨元,从而销售量减少 个,共售出个
∴
∴时,元
四、课堂运用
答案与解析
1.【答案】(-∞,-3]
【解析】由二次函数的性质,可知4≤-(a-1),
解得a≤-3.
2.【答案】①
【解析】∵在定义域上是增函数,
∴,即函数最小值为,无最大值.
3.【答案】[1,2]
【解析】由y=x2-2x+3=(x-1)2+2知,
当x=1时,y的最小值为2,
当y=3时,x2-2x+3=3,解得x=0或x=2.
由y=x2-2x+3的图象知,当m∈[1,2]时,能保证y的最大值为3,最小值为2.
4.【答案】-2 0
【解析】y=-(x-3)2+18,∵a
得b=0(b=6不合题意,舍去)
-a2+6a+9=-7,得a=-2(a=8不合题意,舍去).
5.【答案】2
【解析】函数在上是单调递增函数,
故.
6.【答案】
【解析】由已知,可得,即函数是定义在区间上的二次函数.将二次函数配方得,其对称轴方程,顶点坐标,且图象开口向上.显然其顶点横坐标不在区间内,如图所示。函数的最小值为,最大值为.
7.【答案】
【解析】令 有,则 ,
8.【答案】
【解析】函数,其对称轴方程为,顶点坐标为,图象开口向上.
如图1所示,若顶点横坐标在区间左侧时,有,此时,当时,函数取得最小值.
图1
如图2所示,若顶点横坐标在区间上时,有,即。当时,函数取得最小值.
图2
如图3所示,若顶点横坐标在区间右侧时,有,即。当时,函数取得最小值.
综上讨论,
图3
9.【答案】同解析
【解析】(1)∵f(x)=x2-2x+2=(x-1)2+1,,
∴f(x)的最小值是f(1)=1,
又, f(3)=5,
所以,f(x)的最大值是f(3)=5,
即f(x)在区间上的最大值是5,最小值是1.
(2)∵g(x)=f(x)-mx=x2-(m+2)x+2,
∴或,即m≤2或m≥6.
故m的取值范围是(-∞,2]∪[6,+∞).
10.【答案】同解析
【解析】(1)设f(x)=ax2+bx+c(a≠0),由f(0)=1,∴c=1,
∴f(x)=ax2+bx+1.
∵f(x+1)-f(x)=2x, ∴2ax+a+b=2x,
∴∴f(x)=x2-x+1.
(2)由题意:x2-x+1>2x+m在[-1,1]上恒成立,
即x2-3x+1-m>0在[-1,1]上恒成立.
令,
其对称轴为,
∴g(x)在区间[-1,1]上是减函数, ∴g(x)min=g(1)=1-3+1-m>0,
∴m<-1.
11.【答案】
【解析】将代入中,得
,即时,
,即时,
所以 .
12.【答案】或
【解析】
(1)若,不符合题意.
(2)若则,由,得.
(3)若时,则,由,得.
综上知或.
课后作业
1.【答案】f(0)
二次函数的对称轴为x=,
因为f(x)=x2+bx+c开口向上,
且f(0)=f(1),f(-2)=f(3),
由函数f(x)的图象可知,[,+∞)为f(x)的增区间,
所以f(1)
【解析】y=|x-3|-|x+1|=.
因为[-1,3)是函数y=-2x+2的减区间,
所以-4≤y≤4,综上可知③正确.
3.【答案】
【解析】
4.【答案】
【解析】令
原函数得最大值为
5.【答案】函数的最小值是,最大值是.
【解析】由已知有,于是函数是定义在区间上的二次函数,将配方得:.
二次函数的对称轴方程是顶点坐标为,图象开口向上
由可得,显然其顶点横坐标在区间的左侧或左端点上.
函数的最小值是,最大值是.
6.【答案】
【解析】:由已知可求对称轴为.
(1)当时,.
(2)当,即时,.
根据对称性,若即时,.
若即时,.
(3)当即时,.
综上,
7.【答案】
【解析】函数图象的对称轴方程为,应分,,即,和这三种情形讨论,下列三图分别为
(1);由图可知
(2);由图可知
(3) 时;由图可知
;即
8.【答案】同解析
【解析】(1)当a=1时,f(x)=x2-|x|+1
=
作图(如右所示)
(2)当x∈[1,2]时,f(x)=ax2-x+2a-1.
若a=0,则f(x)=-x-1在区间[1,2]上是减函数,
g(a)=f(2)=-3.
若a>0,则
f(x)图象的对称轴是直线x=.
当0<<1,即a>时,f(x)在区间[1,2]上是增函数,
g(a)=f(1)=3a-2.
当1≤≤2,即≤a≤时,
g(a)==,
当>2,即0
综上可得g(a)=
9.【答案】
【解析】讨论对称轴中 与的位置关系。
①若,则,解得
②若,则,无解
③若,则,无解
④若,则,无解
综上,.
10.【答案】
【解析】令,得.
由于,得.因此.
.
当时有最小值;当时有最大值.
故的值域为.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
