2021-2022学年冀教版八年级上册数学期中复习试卷(Word版,附答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级上册数学期中复习试卷(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 17:51:25 | ||
图片预览



文档简介
2021-2022学年冀教新版八年级上册数学期中复习试卷
一.选择题
1.在、、、、、+x中,分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
3.下列6个数中:﹣3,,﹣π,,0.12,﹣0.5050050005…(相邻两个5之间0的个数逐次加1).其中是无理数的有( )
A.2个 B.3个 C.4个 D.5个
4.下列计算正确的是( )
A.=x B.= C.2÷2﹣1=﹣1 D.a﹣3=(a3)﹣1
5.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠BAD=∠CAE B.AC=DE C.∠ABC=∠AED D.AB=AE
6.49的平方根等于( )
A. B.7 C.±7 D.±
7.已知,则的值等于( )
A.2 B.﹣2 C.4 D.﹣4
8.下列说法:①﹣3是的平方根;②﹣7是(﹣7)2的算术平方根;③125的立方根是±5;④﹣16的平方根是±4;⑤0没有算术平方根.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
9.下列说法正确的是( )
A.式子一定是二次根式
B.带二次根号的式子一定是二次根式
C.式子一定是二次根式
D.二次根式的值必定是无理数
10.要使有意义,则( )
A.x≥﹣5 B.x≤﹣5 C.x<﹣5 D.x>﹣5
11.下列计算正确的是( )
A.()2=2 B.=﹣2 C.=2 D.(﹣)2=﹣2
12.计算(+)=( )
A. + B. + C. + D. +
二.填空题
13.数轴上到﹣这点距离为的点表示的数是 .
14.已知:,m,n均为正整数,则mn的最小值为 .
15.如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
16.已知关于x的方程=3的解是非负数,则m的取值范围是 .
17.如果关于x的方程有增根,那么k= .
三.解答题
18.解方程.
(1)=.
(2)+2=.
19.已知与|b+2|互为相反数,求(a﹣b)2的值.
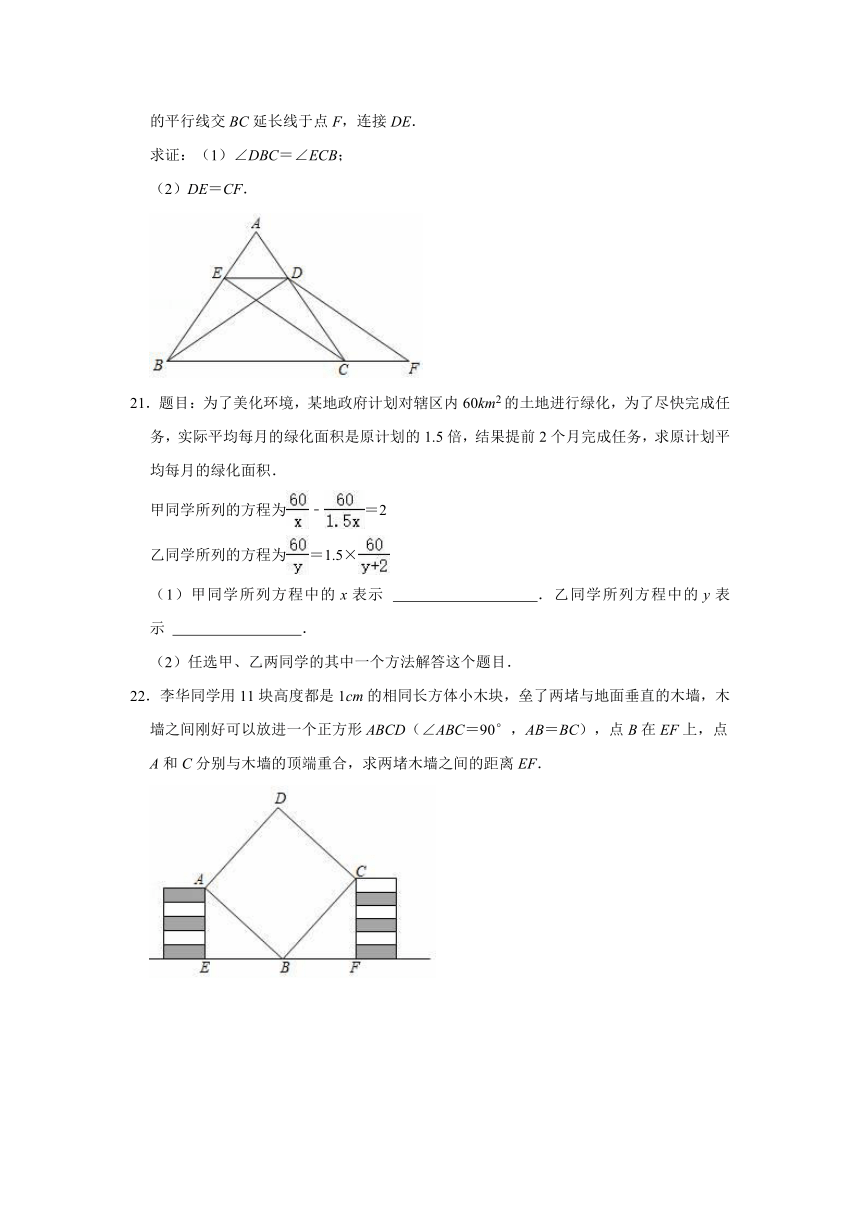
20.已知:如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,过点D作CE的平行线交BC延长线于点F,连接DE.
求证:(1)∠DBC=∠ECB;
(2)DE=CF.
21.题目:为了美化环境,某地政府计划对辖区内60km2的土地进行绿化,为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务,求原计划平均每月的绿化面积.
甲同学所列的方程为﹣=2
乙同学所列的方程为=1.5×
(1)甲同学所列方程中的x表示 .乙同学所列方程中的y表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
22.李华同学用11块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
参考答案与试题解析
一.选择题
1.解:、、+x是分式,
故选:B.
2.解:①有一个外角是120°的等腰三角形是等边三角形,命题正确;
②有两个外角相等的等腰三角形是等边三角形,命题错误;
③有一边上的高也是这边上的中线的三角形是等边三角形,命题错误;
④三个外角都相等的三角形是等边三角形,命题正确,
正确的命题有2个,
故选:C.
3.解:无理数有﹣π,,﹣0.5050050005…(相邻两个5之间0的个数逐次加1),共有3个,
故选:B.
4.解:A、,错误;
B、,错误;
C、2÷2﹣1=4,错误;
D、a﹣3=(a3)﹣1,正确;
故选:D.
5.解:A、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAD﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,本选项结论成立;
B、∵△ABC≌△ADE,
∴AC=AE,而AC与DE不一定相等,本选项结论不成立;
C、∵△ABC≌△ADE,
∴∠C=∠AED,而∠ABC与∠AED不一定相等,本选项结论不成立;
D、∵△ABC≌△ADE,
∴AB=AD,而AB与AE不一定相等,本选项结论不成立;
故选:A.
6.解:±=±7,
故选:C.
7.解:∵(x﹣1)2+=0,
∴x﹣1=0,y+4=0,
解得:x=1,y=﹣4,
===4.
故选:C.
8.解::①﹣3是的平方根;故①正确,
②7是(﹣7)2的算术平方根;故②错误,
③125的立方根是5,故③错误;
④负数没有平方根,故④错误,
⑤0的算术平方根是0,故⑤错误.
故选:A.
9.解:A、在实数范围内,2x2+1≥0,则式子一定是二次根式,故本选项正确;
B、若被开方数是负数,此时不是二次根式,故本选项错误;
C、当x=0时,无意义,则式子无意义,故本选项错误;
D、=2,此时不是无理数,故本选项错误;
故选:A.
10.解:由题意得,x+5≥0,
解得x≥﹣5.
故选:A.
11.解:A、()2=2,故此选项符合题意;
B、=2,故此选项不合题意;
C、=2,故此选项不合题意;
D、(﹣)2=2,故此选项不合题意;
故选:A.
12.解:原式=×+×=+,
故选:D.
二.填空题
13.解:数轴上到﹣这点距离为的点表示的数是0或﹣2,
故答案为:0或﹣2
14.解:原式=5﹣=m﹣n,
∵m,n均为正整数,
∴n的最小值为1,此时m最小值为5,
∴mn的最小值为5×1=5,
故答案为:5.
15.解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=60,
∴7t=60﹣3t,
解得:t=6,
∴AG=BE=3t=3×6=18;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=60,
∴3t=60﹣3t,
解得:t=10,
∴AG=BF=7t=7×10=70,
综上所述,AG=18或AG=70.
故答案为:18或70.
16.解:分式方程去分母得:2x+m=3x﹣9,
解得:x=m+9,
由分式方程的解是非负数,得到m+9≥0,且m+9≠3,
解得:m≥﹣9且m≠﹣6,
故答案为:m≥﹣9且m≠﹣6
17.解:,
去分母得:1=3(x﹣3)+k,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得1=3(3﹣3)+k,
解得k=1.
故答案为:1.
三.解答题
18.解:(1)去分母,得
5(2x+1)=x﹣1,
去括号,得
10x+5=x﹣1,
移项,合并同类项,得
9x=﹣6,
系数化为1,得
x=﹣,
检验:把x=﹣代入(x﹣1)(2x+1)≠0,
所以x=﹣是原方程的解;
(2)去分母,得
1+2(x﹣2)=x﹣1,
去括号,得
1+2x﹣4=x﹣1,
移项,合并同类项,得
x=2,
检验:把x=2代入x﹣2=0,
所以此方程无解.
19.解:∵与|b+2|互为相反数,
∴2a﹣2=0,b+2=0,
∴a=1,b=﹣2,
则(a﹣b)2=(1+2)2=9;
20.证明:(1)∵BD⊥AC于点D,CE⊥AB于点E,
∴∠AEC=∠ADB=90°,
在Rt△ACE和Rt△ABD中,
∴△ACE≌△ABD(AAS)
∴AE=AD,CE=BD,
∴∠AED=∠ADE,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠AED+∠ADE+∠A=∠ABC+∠ACB+∠A=180°,
∴∠AED=∠ABC,
∴ED∥BC,
∵CE∥FD,
∴四边形ECFD为平行四边形,∠ECB=∠F,
∴CE=FD,
∴BD=FD,
∴∠DBC=∠F,
∴∠DBC=∠ECB;
(2)∵四边形ECFD为平行四边形,
∴DE=CF.
21.解:(1)由题意可得,
甲同学所列方程中的x表示原计划平均每月的绿化面积,乙同学所列方程中的y表示实际完成这项工程需要的月数,
故答案为:原计划平均每月的绿化面积;实际完成这项工程需要的月数;
(2)按甲同学的作法解答,
﹣=2,
方程两边同乘以1.5x,得
90﹣60=3x,
解得,x=10,
经检验,x=10是原分式方程的解,
答:原计划平均每月的绿化面积是10km2.
22.解:∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,
∵∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=5cm,BE=CF=6cm,
∴EF=5+6=11(cm).
一.选择题
1.在、、、、、+x中,分式的个数有( )
A.2个 B.3个 C.4个 D.5个
2.在下列命题中:①有一个外角是120°的等腰三角形是等边三角形;②有两个外角相等的等腰三角形是等边三角形;③有一边上的高也是这边上的中线的三角形是等边三角形;④三个外角都相等的三角形是等边三角形.正确的命题有( )
A.4个 B.3个 C.2个 D.1个
3.下列6个数中:﹣3,,﹣π,,0.12,﹣0.5050050005…(相邻两个5之间0的个数逐次加1).其中是无理数的有( )
A.2个 B.3个 C.4个 D.5个
4.下列计算正确的是( )
A.=x B.= C.2÷2﹣1=﹣1 D.a﹣3=(a3)﹣1
5.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠BAD=∠CAE B.AC=DE C.∠ABC=∠AED D.AB=AE
6.49的平方根等于( )
A. B.7 C.±7 D.±
7.已知,则的值等于( )
A.2 B.﹣2 C.4 D.﹣4
8.下列说法:①﹣3是的平方根;②﹣7是(﹣7)2的算术平方根;③125的立方根是±5;④﹣16的平方根是±4;⑤0没有算术平方根.其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
9.下列说法正确的是( )
A.式子一定是二次根式
B.带二次根号的式子一定是二次根式
C.式子一定是二次根式
D.二次根式的值必定是无理数
10.要使有意义,则( )
A.x≥﹣5 B.x≤﹣5 C.x<﹣5 D.x>﹣5
11.下列计算正确的是( )
A.()2=2 B.=﹣2 C.=2 D.(﹣)2=﹣2
12.计算(+)=( )
A. + B. + C. + D. +
二.填空题
13.数轴上到﹣这点距离为的点表示的数是 .
14.已知:,m,n均为正整数,则mn的最小值为 .
15.如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为 .
16.已知关于x的方程=3的解是非负数,则m的取值范围是 .
17.如果关于x的方程有增根,那么k= .
三.解答题
18.解方程.
(1)=.
(2)+2=.
19.已知与|b+2|互为相反数,求(a﹣b)2的值.
20.已知:如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,过点D作CE的平行线交BC延长线于点F,连接DE.
求证:(1)∠DBC=∠ECB;
(2)DE=CF.
21.题目:为了美化环境,某地政府计划对辖区内60km2的土地进行绿化,为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务,求原计划平均每月的绿化面积.
甲同学所列的方程为﹣=2
乙同学所列的方程为=1.5×
(1)甲同学所列方程中的x表示 .乙同学所列方程中的y表示 .
(2)任选甲、乙两同学的其中一个方法解答这个题目.
22.李华同学用11块高度都是1cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形ABCD(∠ABC=90°,AB=BC),点B在EF上,点A和C分别与木墙的顶端重合,求两堵木墙之间的距离EF.
参考答案与试题解析
一.选择题
1.解:、、+x是分式,
故选:B.
2.解:①有一个外角是120°的等腰三角形是等边三角形,命题正确;
②有两个外角相等的等腰三角形是等边三角形,命题错误;
③有一边上的高也是这边上的中线的三角形是等边三角形,命题错误;
④三个外角都相等的三角形是等边三角形,命题正确,
正确的命题有2个,
故选:C.
3.解:无理数有﹣π,,﹣0.5050050005…(相邻两个5之间0的个数逐次加1),共有3个,
故选:B.
4.解:A、,错误;
B、,错误;
C、2÷2﹣1=4,错误;
D、a﹣3=(a3)﹣1,正确;
故选:D.
5.解:A、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAD﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,本选项结论成立;
B、∵△ABC≌△ADE,
∴AC=AE,而AC与DE不一定相等,本选项结论不成立;
C、∵△ABC≌△ADE,
∴∠C=∠AED,而∠ABC与∠AED不一定相等,本选项结论不成立;
D、∵△ABC≌△ADE,
∴AB=AD,而AB与AE不一定相等,本选项结论不成立;
故选:A.
6.解:±=±7,
故选:C.
7.解:∵(x﹣1)2+=0,
∴x﹣1=0,y+4=0,
解得:x=1,y=﹣4,
===4.
故选:C.
8.解::①﹣3是的平方根;故①正确,
②7是(﹣7)2的算术平方根;故②错误,
③125的立方根是5,故③错误;
④负数没有平方根,故④错误,
⑤0的算术平方根是0,故⑤错误.
故选:A.
9.解:A、在实数范围内,2x2+1≥0,则式子一定是二次根式,故本选项正确;
B、若被开方数是负数,此时不是二次根式,故本选项错误;
C、当x=0时,无意义,则式子无意义,故本选项错误;
D、=2,此时不是无理数,故本选项错误;
故选:A.
10.解:由题意得,x+5≥0,
解得x≥﹣5.
故选:A.
11.解:A、()2=2,故此选项符合题意;
B、=2,故此选项不合题意;
C、=2,故此选项不合题意;
D、(﹣)2=2,故此选项不合题意;
故选:A.
12.解:原式=×+×=+,
故选:D.
二.填空题
13.解:数轴上到﹣这点距离为的点表示的数是0或﹣2,
故答案为:0或﹣2
14.解:原式=5﹣=m﹣n,
∵m,n均为正整数,
∴n的最小值为1,此时m最小值为5,
∴mn的最小值为5×1=5,
故答案为:5.
15.解:设BE=3t,则BF=7t,因为∠A=∠B=90°,使△AEG与△BEF全等,可分两种情况:
情况一:当BE=AG,BF=AE时,
∵BF=AE,AB=60,
∴7t=60﹣3t,
解得:t=6,
∴AG=BE=3t=3×6=18;
情况二:当BE=AE,BF=AG时,
∵BE=AE,AB=60,
∴3t=60﹣3t,
解得:t=10,
∴AG=BF=7t=7×10=70,
综上所述,AG=18或AG=70.
故答案为:18或70.
16.解:分式方程去分母得:2x+m=3x﹣9,
解得:x=m+9,
由分式方程的解是非负数,得到m+9≥0,且m+9≠3,
解得:m≥﹣9且m≠﹣6,
故答案为:m≥﹣9且m≠﹣6
17.解:,
去分母得:1=3(x﹣3)+k,
由分式方程有增根,得到x﹣3=0,即x=3,
把x=3代入整式方程得1=3(3﹣3)+k,
解得k=1.
故答案为:1.
三.解答题
18.解:(1)去分母,得
5(2x+1)=x﹣1,
去括号,得
10x+5=x﹣1,
移项,合并同类项,得
9x=﹣6,
系数化为1,得
x=﹣,
检验:把x=﹣代入(x﹣1)(2x+1)≠0,
所以x=﹣是原方程的解;
(2)去分母,得
1+2(x﹣2)=x﹣1,
去括号,得
1+2x﹣4=x﹣1,
移项,合并同类项,得
x=2,
检验:把x=2代入x﹣2=0,
所以此方程无解.
19.解:∵与|b+2|互为相反数,
∴2a﹣2=0,b+2=0,
∴a=1,b=﹣2,
则(a﹣b)2=(1+2)2=9;
20.证明:(1)∵BD⊥AC于点D,CE⊥AB于点E,
∴∠AEC=∠ADB=90°,
在Rt△ACE和Rt△ABD中,
∴△ACE≌△ABD(AAS)
∴AE=AD,CE=BD,
∴∠AED=∠ADE,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠AED+∠ADE+∠A=∠ABC+∠ACB+∠A=180°,
∴∠AED=∠ABC,
∴ED∥BC,
∵CE∥FD,
∴四边形ECFD为平行四边形,∠ECB=∠F,
∴CE=FD,
∴BD=FD,
∴∠DBC=∠F,
∴∠DBC=∠ECB;
(2)∵四边形ECFD为平行四边形,
∴DE=CF.
21.解:(1)由题意可得,
甲同学所列方程中的x表示原计划平均每月的绿化面积,乙同学所列方程中的y表示实际完成这项工程需要的月数,
故答案为:原计划平均每月的绿化面积;实际完成这项工程需要的月数;
(2)按甲同学的作法解答,
﹣=2,
方程两边同乘以1.5x,得
90﹣60=3x,
解得,x=10,
经检验,x=10是原分式方程的解,
答:原计划平均每月的绿化面积是10km2.
22.解:∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠EAB+∠ABE=90°,
∵∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠EAB=∠CBF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF=5cm,BE=CF=6cm,
∴EF=5+6=11(cm).
同课章节目录
