2021-2022学年沪科新版九年级上册数学期中复习试卷(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年沪科新版九年级上册数学期中复习试卷(Word版,附答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 399.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 00:00:00 | ||
图片预览



文档简介
2021-2022学年沪科新版九年级上册数学期中复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.抛物线y=3(x+4)2+2的顶点坐标是( )
A.(2,4) B.(2,﹣4) C.(4,2) D.(﹣4,2)
2.a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,则线段d的长为( )
A.3cm B.4cm C.5cm D.6cm
3.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.= B.= C.= D.=
4.如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A. += B. += C. += D. +=
5.将抛物线y=﹣(x+1)2+3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为( )
A.y=﹣(x+3)2+1 B.y=﹣(x﹣1)2+5
C.y=﹣(x+1)2+5 D.y=﹣(x+3)2+5
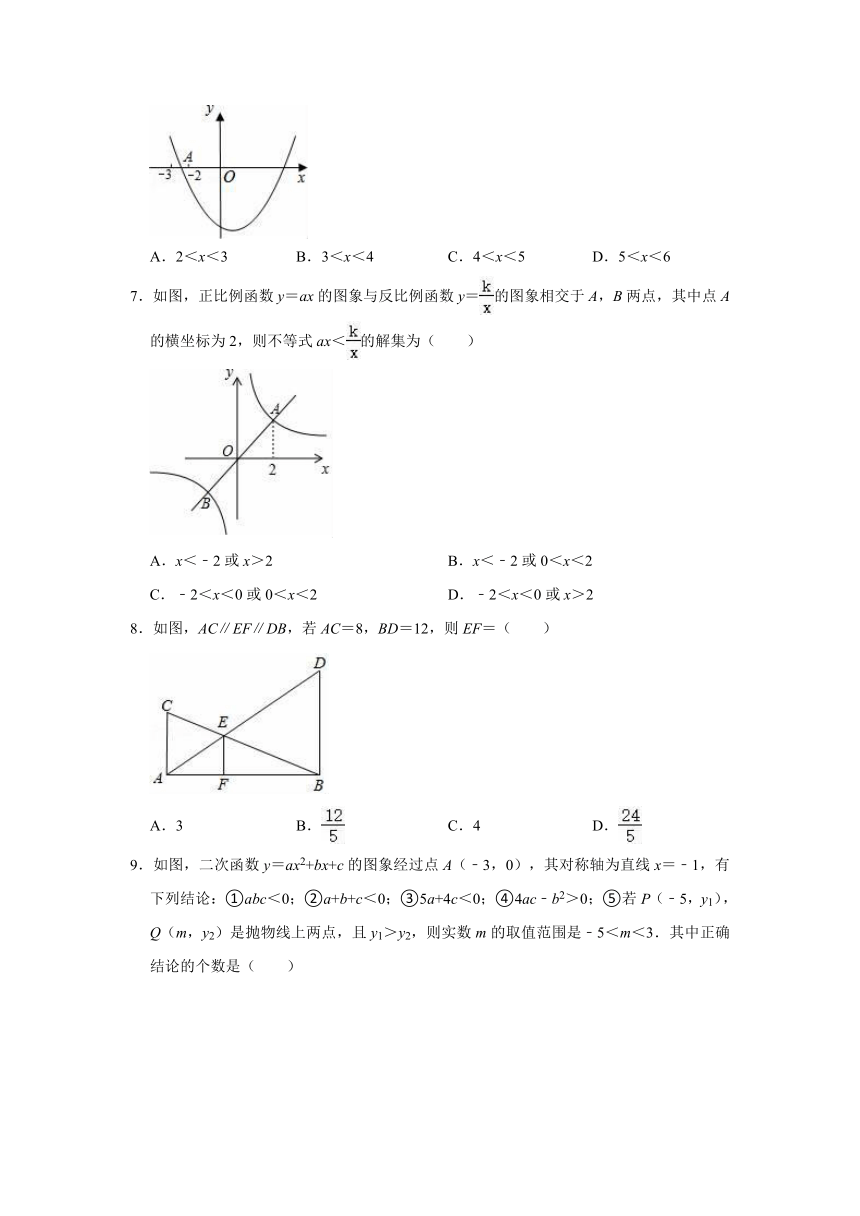
6.如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
7.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于A,B两点,其中点A的横坐标为2,则不等式ax<的解集为( )
A.x<﹣2或x>2 B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<2 D.﹣2<x<0或x>2
8.如图,AC∥EF∥DB,若AC=8,BD=12,则EF=( )
A.3 B. C.4 D.
9.如图,二次函数y=ax2+bx+c的图象经过点A(﹣3,0),其对称轴为直线x=﹣1,有下列结论:①abc<0;②a+b+c<0;③5a+4c<0;④4ac﹣b2>0;⑤若P(﹣5,y1),Q(m,y2)是抛物线上两点,且y1>y2,则实数m的取值范围是﹣5<m<3.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
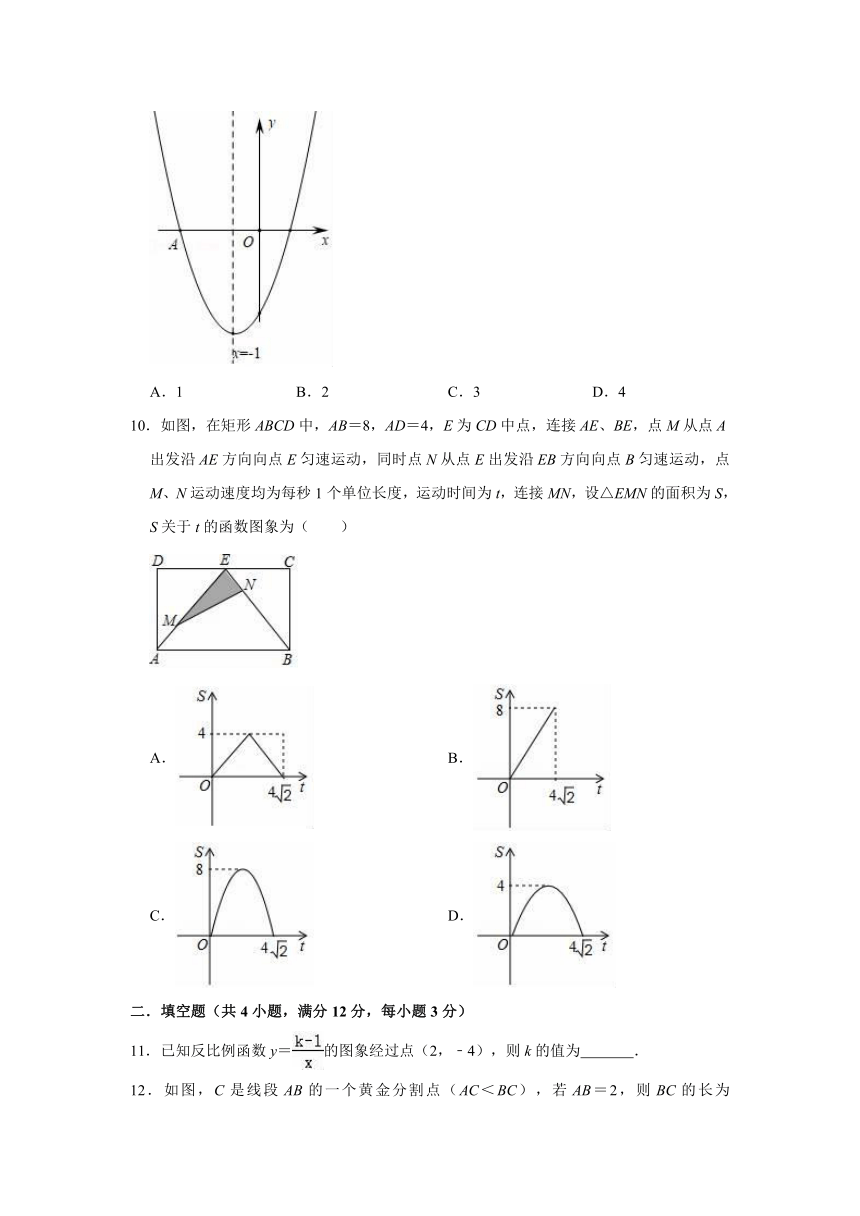
10.如图,在矩形ABCD中,AB=8,AD=4,E为CD中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,S关于t的函数图象为( )
A. B.
C. D.
二.填空题(共4小题,满分12分,每小题3分)
11.已知反比例函数y=的图象经过点(2,﹣4),则k的值为 .
12.如图,C是线段AB的一个黄金分割点(AC<BC),若AB=2,则BC的长为 (结果保留根号).
13.如图,在矩形ABCD中,AD>AB,AB=2.点E在矩形ABCD的边BC上,连接AE,将矩形ABCD沿AE翻折,翻折后的点B落在边AD上的点F处,得到矩形CDFE.若矩形CDFE与原矩形ABCD相似,则AD的长为 .
14.抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②m(am+b)<a+b(m≠1的实数);③﹣3a=c;④将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;⑤点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为+.其中正确的是 .
三.解答题(共2小题,满分16分,每小题8分)
15.(1)已知=,求x:y的值.
(2)已知线段a=3,b=6,求线段a,b的比例中项.
16.已知二次函数y=﹣x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
四.解答题(共2小题,满分16分,每小题8分)
17.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
18.如图,△ABC的三条中线相交于一点O,图中哪些三角形面积分别相等?为什么?
五.解答题(共2小题,满分20分,每小题10分)
19.我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓,我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台,经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低1元,就可多售出5台,若供货商规定这种空气净化器售价不低于330元/台,代理销售商每月要完成不低于450台的销售任务.
(1)若某月空气净化器售价降低30元,则该月可售出多少台?
(2)试确定月销售量y(台)与售价x(元/台)之间的函数关系式,并求出售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获的利润w(元)最大,最大利润是多少?
20.如图,已知直线y=﹣2x+3与抛物线y=x2相交于A,B两点,O为坐标原点.
(1)求点A和B的坐标;
(2)连接OA,OB,求△OAB的面积.
六.解答题(共1小题,满分12分,每小题12分)
21.如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
七.解答题(共1小题,满分12分,每小题12分)
22.某公司分别在A,B两城生产同种产品,共100件.A城生产产品的成本y(万元)与产品数量x(件)之间具有函数关系y=x2+20x+100,B城生产产品的每件成本为60万元.
(1)当A城生产多少件产品时,A,B两城生产这批产品成本的和最小,最小值是多少?
(2)从A城把该产品运往C,D两地的费用分别为1万元/件和3万元/件;从B城把该产品运往C,D两地的费用分别为1万元/件和2万元/件.C地需要90件,D地需要10件,在(1)的条件下,怎样调运可使A,B两城运费的和最小?
八.解答题(共1小题,满分12分,每小题12分)
23.如图,在Rt△ABC中,∠C=90°,D是AC边上的一点,DE⊥AB于点E.
(1)求证:△ABC∽△ADE;
(2)如果AC=4,BC=3,DE=2,求AD的长.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:∵y=3(x+4)2+2是抛物线解析式的顶点式,
∴根据顶点式的坐标特点可知,顶点坐标为(﹣4,2).
故选:D.
2.解:根据题意得a:b=c:d,即3:2=6:d,
所以d==4(cm).
故选:B.
3.解:∵∠BAC=∠D,,
∴△ABC∽△DEA.
故选:C.
4.解:∵AC∥EF,
∴,
∵EF∥DB,
∴,
∴=+===1,即=1,
∴.
故选:C.
5.解:抛物线y=﹣(x+1)2+3的顶点坐标为(﹣1,3),把点(﹣1,3)向右平移2个单位,向上平移2个单位得到对应点的坐标为(1,5),所以平移后的抛物线解析式为y=﹣(x﹣1)2+5,
故选:B.
6.解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
7.解:∵正比例函数y=ax的图象与反比例函数y=的图象相交于A,B两点,
∴A,B两点坐标关于原点对称,
∵点A的横坐标为2,
∴B点的横坐标为﹣2,
∵ax<,
∴在第一和第三象限,正比例函数y=ax的图象在反比例函数y=的图象的下方,
∴x<﹣2或0<x<2,
故选:B.
8.解:∵AC∥EF,
∴△BEF∽△BCA,
∴=,
同理,=,
∴+=+=1,
∴+=1,
解得,EF=,
故选:D.
9.解:①观察图象可知:
a>0,b>0,c<0,∴abc<0,
∴①正确;
②当x=1时,y=0,即a+b+c=0,
∴②错误;
③对称轴x=﹣1,即﹣=﹣1
得b=2a,
当x=时,y<0,
即a+b+c<0,
即a+2b+4c<0,
∴5a+4c<0.
∴③正确;
④因为抛物线与x轴有两个交点,
所以Δ>0,即b2﹣4ac>0,
∴4ac﹣b2<0.
∴④错误;
⑤∵(﹣5,y1)关于直线x=﹣1的对称点的坐标是(3,y1),
∴当y1>y2时,﹣5<m<3.
∴⑤正确.
故选:C.
10.
解:连MB
由勾股定理AE=BE=4
已知,AM=t,EN=t,ME=NB=4﹣t
∵
∴
∵
∴
∴
∵a=﹣0
∴当t=2时,S的最大值为4
故选:D.
二.填空题(共4小题,满分12分,每小题3分)
11.解:∵反比例函数y=的图象经过点(2,﹣4),
∴k﹣1=2×(﹣4)=﹣8,
解得k=﹣7.
故答案为﹣7.
12.解:∵C是线段AB的一个黄金分割点(AC<BC),AB=2,
∴BC=AB=×2=﹣1,
故答案为:﹣1.
13.解:∵矩形CDFE∽矩形ADCB,
∴=,即=,
整理得,AD2﹣2AD﹣4=0,
解得,AD1=1﹣(舍去),AD2=1+,
故答案为:1+.
14.解:①∵y=﹣x2+2x+m+1,
∴抛物线开口向下,对称轴为直线x=﹣=1,
∵抛物线与x轴的一个交点在2和3之间,顶点为B.
∴抛物线与x轴有两个交点,
∴关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;故①结论正确;
②∵抛物线开口向下,抛物线的对称轴为直线x=1,
∴函数的最大值为y=a+b+c,
∴当m≠1时,am2+bm+c<a+b+c,
∴m(am+b)<a+b(m≠1的实数),故②结论正确;
③∵抛物线的对称轴为直线x=1,与x轴的一个交点在2和3之间,
∴另一个交点在﹣1和0之间,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,
∵﹣=1,
∴b=﹣2a,
∴3a+c<0,
∴﹣3a>c,故③结论错误;
④将该抛物线向左平移2个单位,再向下平移2个单位,抛物线的解析式为:y=﹣(x+2)2+2(x+2)+m+1﹣2,即y=﹣(x+1)2+m,故④结论正确;
⑤当m=1时,抛物线的解析式为y=﹣x2+2x+2,
∴A(0,2),C(2,2),B(1,3),
如图,作点B关于y轴的对称点B'(﹣1,3),作C关于x轴的对称点C'(2,﹣2),
连接B'C',与x轴、y轴分别交于D、E点,则BE+ED+CD+BC=B'E+ED+C'D+BC,
根据两点之间线段最短,知B'C'最短,而BC的长度一定,此时四边形BCDE的周长最小,最小为+,故⑤正确.
故答案为①②④⑤.
三.解答题(共2小题,满分16分,每小题8分)
15.解:(1)∵=,
∴设x=3k,x+y=7k,
∴y=4k,
∴x:y=3k:4k=3:4;
(2)设线段x是线段a,b的比例中项,
∵a=3,b=6,
∴,
∴x2=ab=3×6=18,
∴x=±3(负值舍去).
∴线段a,b的比例中项是3.
16.解:(1)把A(2,0),B(2,﹣6)代入y=﹣x2+bx+c得,解得,
所以抛物线解析式为y=﹣x2+4x﹣6;
(2)抛物线的对称轴为直线x=﹣=4,则C(4,0),
所以△ABC的面积=×(4﹣2)×6=6.
四.解答题(共2小题,满分16分,每小题8分)
17.解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4),
PC⊥OB时,△CPB∽△OAB,根据勾股定理得,OB==10,
∵P(3,4)为OB的中点,
∴PB=OB=5,
∴=,
即=,
解得BC=,
AC=AB﹣BC=8﹣=,
此时点C的坐标为(6,),
综上所述,点C的坐标为(3,0),(6,4),(6,).
18.解:∵△ABC的三条中线相交于一点O,
∴AE=BE,BD=CD,AF=CF,AO=2OD,BO=2OF,OC=2OE,
∴S△ABD=S△ACD=S△BAF=S△BCF=S△CAE=S△CBE=S△ABC,
S△AOE=S△BOE,S△BOD=S△COD,S△AOF=S△COF,
∵点O为重心,
∴S△ABO=S△BCO=S△ACO,
∴S△AOE=S△BOE=S△BOD=S△COD=S△AOF=S△COF.
五.解答题(共2小题,满分20分,每小题10分)
19.解:(1)若某月空气净化器售价降低30元,该月可售出200+5×30=350台.
(2)由题意,得:y=200+5(400﹣x)=2200﹣5x.
∵售价不低于330元/台
∴x≥330
∵数量不低于450台
∴y≥450,
2200﹣5x≥450
x≤350
∴330≤x≤350.
答:y与x之间的函数关系式为:y=2200﹣5x;
(3)由题意,得:w=(x﹣200)(2200﹣5x)=﹣5(x﹣320)2+72000,
∵a=﹣5<0,
∴在对称轴的右侧w随x的增大而减小,
∴x=330时,w最大=71500.
答:当售价为330元/台时,月利润最大为71500元.
20.解:(1)如图,直线y=﹣2x+3与抛物线y=x2相交,
即x2=﹣2x+3,
解得x1=1,x2=﹣3,
因此交点坐标为A为(1,1),B为(﹣3,9);
(2)作AA1,BB1分别垂直于x轴,垂足为A1,B1,
∴S△OAB=S梯形AA1B1B﹣S△AA1O﹣S△BB1O,
=×(1+9)×(1+3)﹣×1×1﹣×9×3,
=6.
六.解答题(共1小题,满分12分,每小题12分)
21.解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
七.解答题(共1小题,满分12分,每小题12分)
22.解:(1)设A,B两城生产这批产品的总成本的和为W(万元),
则W=x2+20x+100+60(100﹣x)
=x2﹣40x+6100
=(x﹣20)2+5700,
∴当x=20时,W取得最小值,最小值为5700万元,
∴A城生产20件,A,B两城生产这批产品成本的和最小,最小值是5700万元;
(2)设从A城把该产品运往C地的产品数量为n件,则从A城把该产品运往D地的产品数量为(20﹣n)件;
从B城把该产品运往C地的产品数量为(90﹣n)件,则从B城把该产品运往D地的产品数量为(10﹣20+n)件,运费的和为P(万元),
由题意得:,
解得10≤n≤20,
P=n+3(20﹣n)+(90﹣n)+2(10﹣20+n)
=n+60﹣3n+90﹣n+2n﹣20
=n﹣2n+130
=﹣n+130,
根据一次函数的性质可得:
P随n的增大而减小,
∴当n=20时,P取得最小值,最小值为110,
∴从A城把该产品运往C地的产品数量为20件,则从A城把该产品运往D地的产品数量为0件;
从B城把该产品运往C地的产品数量为70件,则从B城把该产品运往D地的产品数量为10件时,可使A,B两城运费的和最小.
八.解答题(共1小题,满分12分,每小题12分)
23.(1)证明:∵DE⊥AB,
∴∠AED=∠C=90°,
∵∠A=∠A,
∴△ABC∽△ADE;
(2)解:在Rt△ABC中,
∵AC=4,BC=3,
∴AB==5,
∵△ABC∽△ADE,
∴,
∴=,
∴AD=.
一.选择题(共10小题,满分40分,每小题4分)
1.抛物线y=3(x+4)2+2的顶点坐标是( )
A.(2,4) B.(2,﹣4) C.(4,2) D.(﹣4,2)
2.a、b、c、d是成比例线段,其中a=3cm,b=2cm,c=6cm,则线段d的长为( )
A.3cm B.4cm C.5cm D.6cm
3.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A.= B.= C.= D.=
4.如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
A. += B. += C. += D. +=
5.将抛物线y=﹣(x+1)2+3向右平移2个单位再向上平移2个单位后得到的新抛物线的表达式为( )
A.y=﹣(x+3)2+1 B.y=﹣(x﹣1)2+5
C.y=﹣(x+1)2+5 D.y=﹣(x+3)2+5
6.如图,以(1,﹣4)为顶点的二次函数y=ax2+bx+c的图象与x轴负半轴交于A点,则一元二次方程ax2+bx+c=0的正数解的范围是( )
A.2<x<3 B.3<x<4 C.4<x<5 D.5<x<6
7.如图,正比例函数y=ax的图象与反比例函数y=的图象相交于A,B两点,其中点A的横坐标为2,则不等式ax<的解集为( )
A.x<﹣2或x>2 B.x<﹣2或0<x<2
C.﹣2<x<0或0<x<2 D.﹣2<x<0或x>2
8.如图,AC∥EF∥DB,若AC=8,BD=12,则EF=( )
A.3 B. C.4 D.
9.如图,二次函数y=ax2+bx+c的图象经过点A(﹣3,0),其对称轴为直线x=﹣1,有下列结论:①abc<0;②a+b+c<0;③5a+4c<0;④4ac﹣b2>0;⑤若P(﹣5,y1),Q(m,y2)是抛物线上两点,且y1>y2,则实数m的取值范围是﹣5<m<3.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
10.如图,在矩形ABCD中,AB=8,AD=4,E为CD中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,S关于t的函数图象为( )
A. B.
C. D.
二.填空题(共4小题,满分12分,每小题3分)
11.已知反比例函数y=的图象经过点(2,﹣4),则k的值为 .
12.如图,C是线段AB的一个黄金分割点(AC<BC),若AB=2,则BC的长为 (结果保留根号).
13.如图,在矩形ABCD中,AD>AB,AB=2.点E在矩形ABCD的边BC上,连接AE,将矩形ABCD沿AE翻折,翻折后的点B落在边AD上的点F处,得到矩形CDFE.若矩形CDFE与原矩形ABCD相似,则AD的长为 .
14.抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.有下列结论:①关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;②m(am+b)<a+b(m≠1的实数);③﹣3a=c;④将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;⑤点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为+.其中正确的是 .
三.解答题(共2小题,满分16分,每小题8分)
15.(1)已知=,求x:y的值.
(2)已知线段a=3,b=6,求线段a,b的比例中项.
16.已知二次函数y=﹣x2+bx+c的图象经过A(2,0),B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
四.解答题(共2小题,满分16分,每小题8分)
17.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分.在图上画出所有线段PC,使分割得到的三角形与Rt△OAB相似,并直接写出点C的坐标.
18.如图,△ABC的三条中线相交于一点O,图中哪些三角形面积分别相等?为什么?
五.解答题(共2小题,满分20分,每小题10分)
19.我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓,我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台,经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低1元,就可多售出5台,若供货商规定这种空气净化器售价不低于330元/台,代理销售商每月要完成不低于450台的销售任务.
(1)若某月空气净化器售价降低30元,则该月可售出多少台?
(2)试确定月销售量y(台)与售价x(元/台)之间的函数关系式,并求出售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获的利润w(元)最大,最大利润是多少?
20.如图,已知直线y=﹣2x+3与抛物线y=x2相交于A,B两点,O为坐标原点.
(1)求点A和B的坐标;
(2)连接OA,OB,求△OAB的面积.
六.解答题(共1小题,满分12分,每小题12分)
21.如图,一次函数y1=ax+b与反比例函数y2=的图象相交于A(2,8),B(8,2)两点,连接AO,BO,延长AO交反比例函数图象于点C.
(1)求一次函数y1的表达式与反比例函数y2的表达式;
(2)当y1<y2,时,直接写出自变量x的取值范围为 ;
(3)点P是x轴上一点,当S△PAC=S△AOB时,请直接写出点P的坐标为 .
七.解答题(共1小题,满分12分,每小题12分)
22.某公司分别在A,B两城生产同种产品,共100件.A城生产产品的成本y(万元)与产品数量x(件)之间具有函数关系y=x2+20x+100,B城生产产品的每件成本为60万元.
(1)当A城生产多少件产品时,A,B两城生产这批产品成本的和最小,最小值是多少?
(2)从A城把该产品运往C,D两地的费用分别为1万元/件和3万元/件;从B城把该产品运往C,D两地的费用分别为1万元/件和2万元/件.C地需要90件,D地需要10件,在(1)的条件下,怎样调运可使A,B两城运费的和最小?
八.解答题(共1小题,满分12分,每小题12分)
23.如图,在Rt△ABC中,∠C=90°,D是AC边上的一点,DE⊥AB于点E.
(1)求证:△ABC∽△ADE;
(2)如果AC=4,BC=3,DE=2,求AD的长.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:∵y=3(x+4)2+2是抛物线解析式的顶点式,
∴根据顶点式的坐标特点可知,顶点坐标为(﹣4,2).
故选:D.
2.解:根据题意得a:b=c:d,即3:2=6:d,
所以d==4(cm).
故选:B.
3.解:∵∠BAC=∠D,,
∴△ABC∽△DEA.
故选:C.
4.解:∵AC∥EF,
∴,
∵EF∥DB,
∴,
∴=+===1,即=1,
∴.
故选:C.
5.解:抛物线y=﹣(x+1)2+3的顶点坐标为(﹣1,3),把点(﹣1,3)向右平移2个单位,向上平移2个单位得到对应点的坐标为(1,5),所以平移后的抛物线解析式为y=﹣(x﹣1)2+5,
故选:B.
6.解:∵二次函数y=ax2+bx+c的顶点为(1,﹣4),
∴对称轴为x=1,
而对称轴左侧图象与x轴交点横坐标的取值范围是﹣3<x<﹣2,
∴右侧交点横坐标的取值范围是4<x<5.
故选:C.
7.解:∵正比例函数y=ax的图象与反比例函数y=的图象相交于A,B两点,
∴A,B两点坐标关于原点对称,
∵点A的横坐标为2,
∴B点的横坐标为﹣2,
∵ax<,
∴在第一和第三象限,正比例函数y=ax的图象在反比例函数y=的图象的下方,
∴x<﹣2或0<x<2,
故选:B.
8.解:∵AC∥EF,
∴△BEF∽△BCA,
∴=,
同理,=,
∴+=+=1,
∴+=1,
解得,EF=,
故选:D.
9.解:①观察图象可知:
a>0,b>0,c<0,∴abc<0,
∴①正确;
②当x=1时,y=0,即a+b+c=0,
∴②错误;
③对称轴x=﹣1,即﹣=﹣1
得b=2a,
当x=时,y<0,
即a+b+c<0,
即a+2b+4c<0,
∴5a+4c<0.
∴③正确;
④因为抛物线与x轴有两个交点,
所以Δ>0,即b2﹣4ac>0,
∴4ac﹣b2<0.
∴④错误;
⑤∵(﹣5,y1)关于直线x=﹣1的对称点的坐标是(3,y1),
∴当y1>y2时,﹣5<m<3.
∴⑤正确.
故选:C.
10.
解:连MB
由勾股定理AE=BE=4
已知,AM=t,EN=t,ME=NB=4﹣t
∵
∴
∵
∴
∴
∵a=﹣0
∴当t=2时,S的最大值为4
故选:D.
二.填空题(共4小题,满分12分,每小题3分)
11.解:∵反比例函数y=的图象经过点(2,﹣4),
∴k﹣1=2×(﹣4)=﹣8,
解得k=﹣7.
故答案为﹣7.
12.解:∵C是线段AB的一个黄金分割点(AC<BC),AB=2,
∴BC=AB=×2=﹣1,
故答案为:﹣1.
13.解:∵矩形CDFE∽矩形ADCB,
∴=,即=,
整理得,AD2﹣2AD﹣4=0,
解得,AD1=1﹣(舍去),AD2=1+,
故答案为:1+.
14.解:①∵y=﹣x2+2x+m+1,
∴抛物线开口向下,对称轴为直线x=﹣=1,
∵抛物线与x轴的一个交点在2和3之间,顶点为B.
∴抛物线与x轴有两个交点,
∴关于x的方程﹣x2+2x+m+1(m为常数)=0有两个不相等的实数根;故①结论正确;
②∵抛物线开口向下,抛物线的对称轴为直线x=1,
∴函数的最大值为y=a+b+c,
∴当m≠1时,am2+bm+c<a+b+c,
∴m(am+b)<a+b(m≠1的实数),故②结论正确;
③∵抛物线的对称轴为直线x=1,与x轴的一个交点在2和3之间,
∴另一个交点在﹣1和0之间,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,
∵﹣=1,
∴b=﹣2a,
∴3a+c<0,
∴﹣3a>c,故③结论错误;
④将该抛物线向左平移2个单位,再向下平移2个单位,抛物线的解析式为:y=﹣(x+2)2+2(x+2)+m+1﹣2,即y=﹣(x+1)2+m,故④结论正确;
⑤当m=1时,抛物线的解析式为y=﹣x2+2x+2,
∴A(0,2),C(2,2),B(1,3),
如图,作点B关于y轴的对称点B'(﹣1,3),作C关于x轴的对称点C'(2,﹣2),
连接B'C',与x轴、y轴分别交于D、E点,则BE+ED+CD+BC=B'E+ED+C'D+BC,
根据两点之间线段最短,知B'C'最短,而BC的长度一定,此时四边形BCDE的周长最小,最小为+,故⑤正确.
故答案为①②④⑤.
三.解答题(共2小题,满分16分,每小题8分)
15.解:(1)∵=,
∴设x=3k,x+y=7k,
∴y=4k,
∴x:y=3k:4k=3:4;
(2)设线段x是线段a,b的比例中项,
∵a=3,b=6,
∴,
∴x2=ab=3×6=18,
∴x=±3(负值舍去).
∴线段a,b的比例中项是3.
16.解:(1)把A(2,0),B(2,﹣6)代入y=﹣x2+bx+c得,解得,
所以抛物线解析式为y=﹣x2+4x﹣6;
(2)抛物线的对称轴为直线x=﹣=4,则C(4,0),
所以△ABC的面积=×(4﹣2)×6=6.
四.解答题(共2小题,满分16分,每小题8分)
17.解:如图,PC∥AB时,△OCP∽△OAB,此时点C的坐标为(3,0),
PC∥OA时,△PCB∽△OAB,此时点C的坐标为(6,4),
PC⊥OB时,△CPB∽△OAB,根据勾股定理得,OB==10,
∵P(3,4)为OB的中点,
∴PB=OB=5,
∴=,
即=,
解得BC=,
AC=AB﹣BC=8﹣=,
此时点C的坐标为(6,),
综上所述,点C的坐标为(3,0),(6,4),(6,).
18.解:∵△ABC的三条中线相交于一点O,
∴AE=BE,BD=CD,AF=CF,AO=2OD,BO=2OF,OC=2OE,
∴S△ABD=S△ACD=S△BAF=S△BCF=S△CAE=S△CBE=S△ABC,
S△AOE=S△BOE,S△BOD=S△COD,S△AOF=S△COF,
∵点O为重心,
∴S△ABO=S△BCO=S△ACO,
∴S△AOE=S△BOE=S△BOD=S△COD=S△AOF=S△COF.
五.解答题(共2小题,满分20分,每小题10分)
19.解:(1)若某月空气净化器售价降低30元,该月可售出200+5×30=350台.
(2)由题意,得:y=200+5(400﹣x)=2200﹣5x.
∵售价不低于330元/台
∴x≥330
∵数量不低于450台
∴y≥450,
2200﹣5x≥450
x≤350
∴330≤x≤350.
答:y与x之间的函数关系式为:y=2200﹣5x;
(3)由题意,得:w=(x﹣200)(2200﹣5x)=﹣5(x﹣320)2+72000,
∵a=﹣5<0,
∴在对称轴的右侧w随x的增大而减小,
∴x=330时,w最大=71500.
答:当售价为330元/台时,月利润最大为71500元.
20.解:(1)如图,直线y=﹣2x+3与抛物线y=x2相交,
即x2=﹣2x+3,
解得x1=1,x2=﹣3,
因此交点坐标为A为(1,1),B为(﹣3,9);
(2)作AA1,BB1分别垂直于x轴,垂足为A1,B1,
∴S△OAB=S梯形AA1B1B﹣S△AA1O﹣S△BB1O,
=×(1+9)×(1+3)﹣×1×1﹣×9×3,
=6.
六.解答题(共1小题,满分12分,每小题12分)
21.解:(1)将A(2,8),B(8,2)代入y=ax+b得,
解得,
∴一次函数为y=﹣x+10,
将A(2,8)代入y2=得8=,解得k=16,
∴反比例函数的解析式为y=;
(2)由图象可知,当y1<y2时,自变量x的取值范围为:x>8或0<x<2,
故答案为x>8或0<x<2;
(3)由题意可知OA=OC,
∴S△APC=2S△AOP,
把y=0代入y1=﹣x+10得,0=﹣x+10,解得x=10,
∴D(10,0),
∴S△AOB=S△AOD﹣S△BOD=﹣=30,
∵S△PAC=S△AOB=×30=24,
∴2S△AOP=24,
∴2××yA=24,即2×OP×8=24,
∴OP=3,
∴P(3,0)或P(﹣3,0),
故答案为P(3,0)或P(﹣3,0).
七.解答题(共1小题,满分12分,每小题12分)
22.解:(1)设A,B两城生产这批产品的总成本的和为W(万元),
则W=x2+20x+100+60(100﹣x)
=x2﹣40x+6100
=(x﹣20)2+5700,
∴当x=20时,W取得最小值,最小值为5700万元,
∴A城生产20件,A,B两城生产这批产品成本的和最小,最小值是5700万元;
(2)设从A城把该产品运往C地的产品数量为n件,则从A城把该产品运往D地的产品数量为(20﹣n)件;
从B城把该产品运往C地的产品数量为(90﹣n)件,则从B城把该产品运往D地的产品数量为(10﹣20+n)件,运费的和为P(万元),
由题意得:,
解得10≤n≤20,
P=n+3(20﹣n)+(90﹣n)+2(10﹣20+n)
=n+60﹣3n+90﹣n+2n﹣20
=n﹣2n+130
=﹣n+130,
根据一次函数的性质可得:
P随n的增大而减小,
∴当n=20时,P取得最小值,最小值为110,
∴从A城把该产品运往C地的产品数量为20件,则从A城把该产品运往D地的产品数量为0件;
从B城把该产品运往C地的产品数量为70件,则从B城把该产品运往D地的产品数量为10件时,可使A,B两城运费的和最小.
八.解答题(共1小题,满分12分,每小题12分)
23.(1)证明:∵DE⊥AB,
∴∠AED=∠C=90°,
∵∠A=∠A,
∴△ABC∽△ADE;
(2)解:在Rt△ABC中,
∵AC=4,BC=3,
∴AB==5,
∵△ABC∽△ADE,
∴,
∴=,
∴AD=.
同课章节目录
