2021-2022学年人教九年级上册数学24.1圆的有关性质 同步训练卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教九年级上册数学24.1圆的有关性质 同步训练卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 527.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 19:52:45 | ||
图片预览

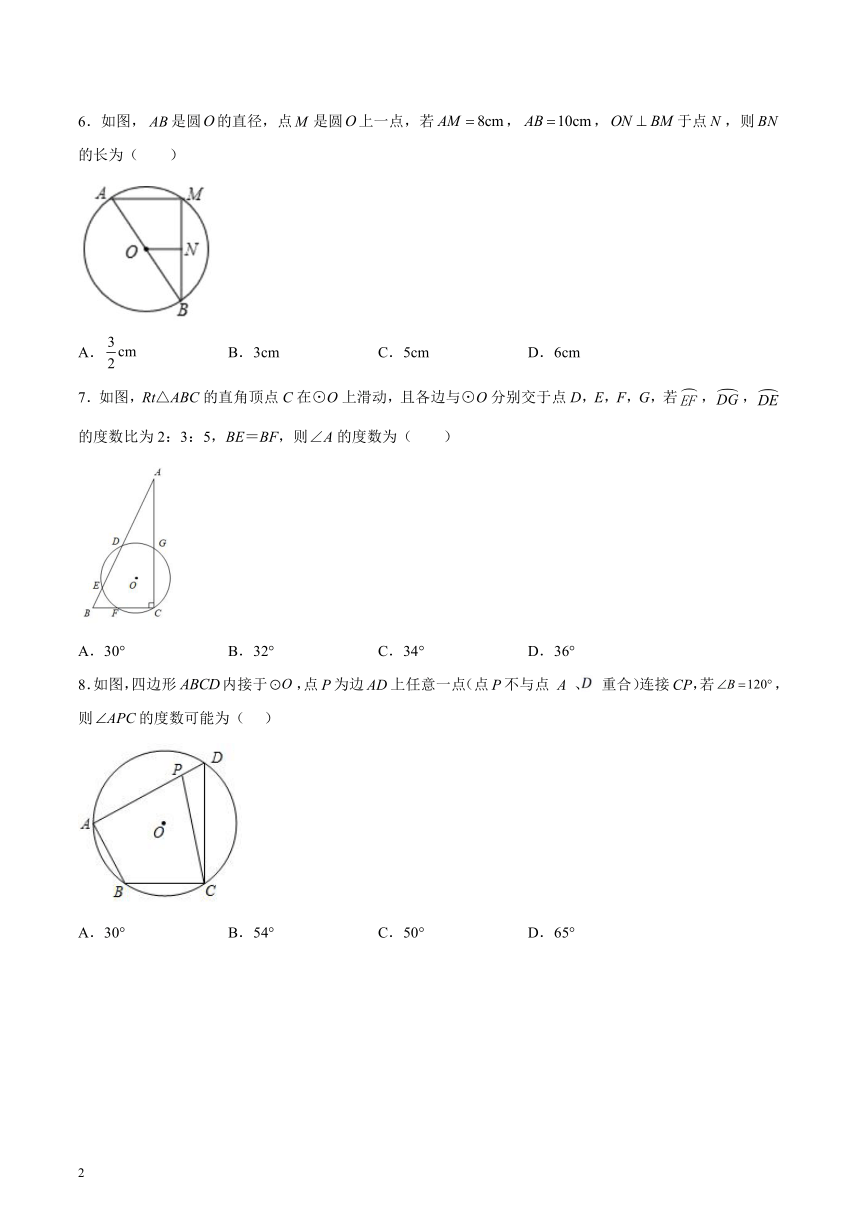
文档简介
第24章24.1圆的有关性质同步训练卷-2021-2022学年人教九年级上册数学
一、单选题
1.下列说法中,正确的是( )
A.两个半圆是等弧 B.同圆中优弧与半圆的差必是劣弧
C.长度相等的弧是等弧 D.直径未必是弦
2.如图,点,,,在圆上,弦和交于点,则下列说法正确的是( )
A.若平分,则 B.若,则平分
C.若垂直平分,则圆心在上 D.若圆心在上,则垂直平分
3.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
5.如图,在⊙O的内接四边形ABCD中,∠BOD=100°,则∠BCD的度数( )
A.130° B.100° C.80° D.50°
6.如图,是圆的直径,点是圆上一点,若,,于点,则的长为( )
A. B.3cm C.5cm D.6cm
7.如图,Rt△ABC的直角顶点C在⊙O上滑动,且各边与⊙O分别交于点D,E,F,G,若,,的度数比为2:3:5,BE=BF,则∠A的度数为( )
A.30° B.32° C.34° D.36°
8.如图,四边形内接于,点P为边AD上任意一点(点P不与点 A 、 重合)连接CP,若,则的度数可能为( )
A.30° B.54° C.50° D.65°
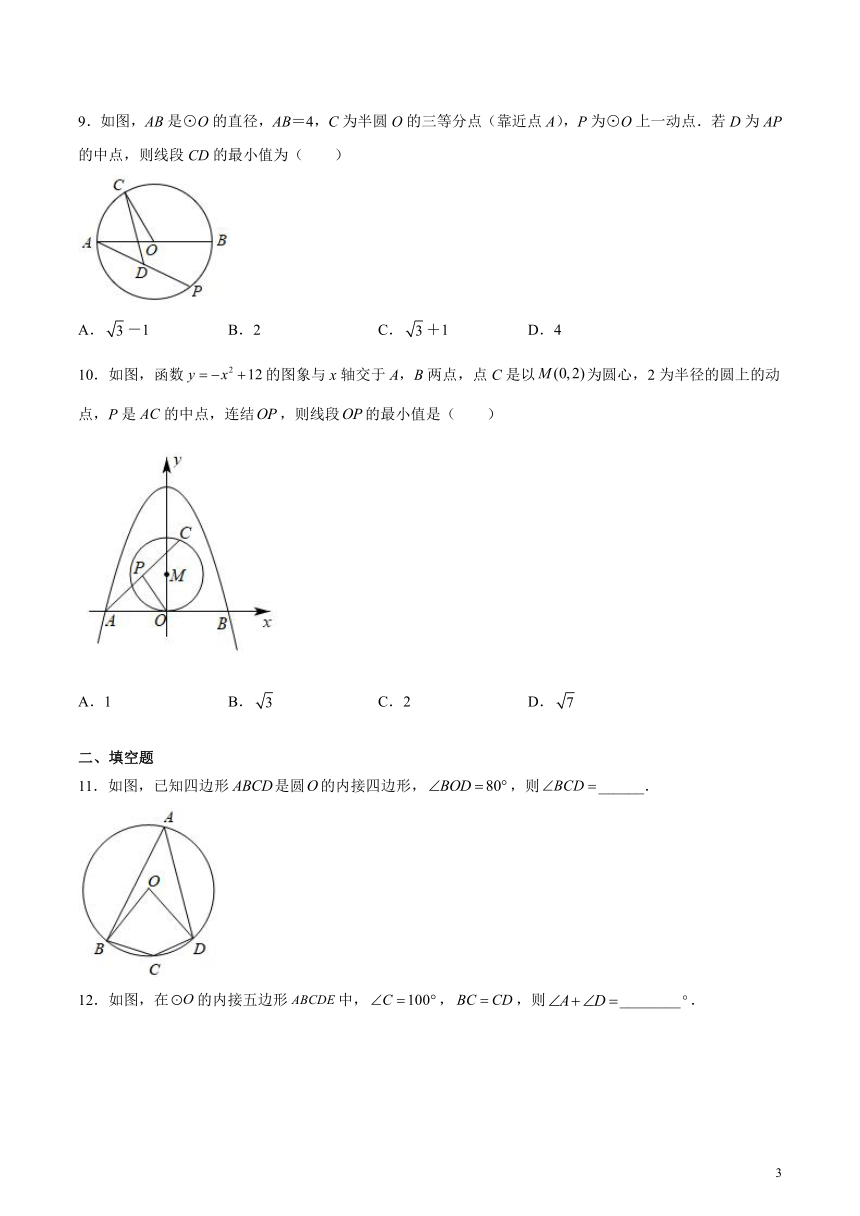
9.如图,AB是⊙O的直径,AB=4,C为半圆O的三等分点(靠近点A),P为⊙O上一动点.若D为AP的中点,则线段CD的最小值为( )
A.-1 B.2 C.+1 D.4
10.如图,函数的图象与x轴交于A,B两点,点C是以为圆心,2为半径的圆上的动点,P是的中点,连结,则线段的最小值是( )
A.1 B. C.2 D.
二、填空题
11.如图,已知四边形是圆的内接四边形,,则______.
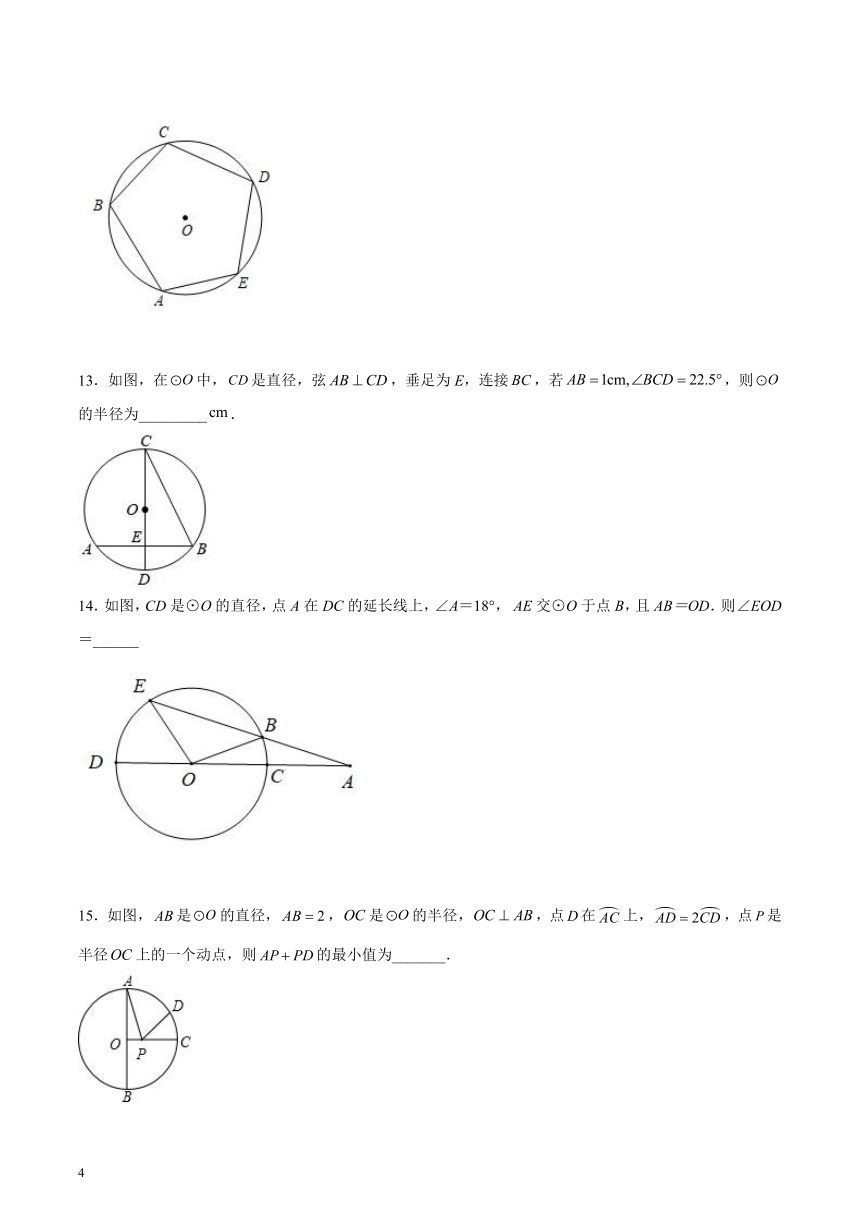
12.如图,在的内接五边形中,,,则________.
13.如图,在中,是直径,弦,垂足为E,连接,若,则的半径为_________.
14.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°, AE交⊙O于点B,且AB=OD.则∠EOD=______
15.如图,是的直径,,是的半径,,点在上,,点是半径上的一个动点,则的最小值为_______.
三、解答题
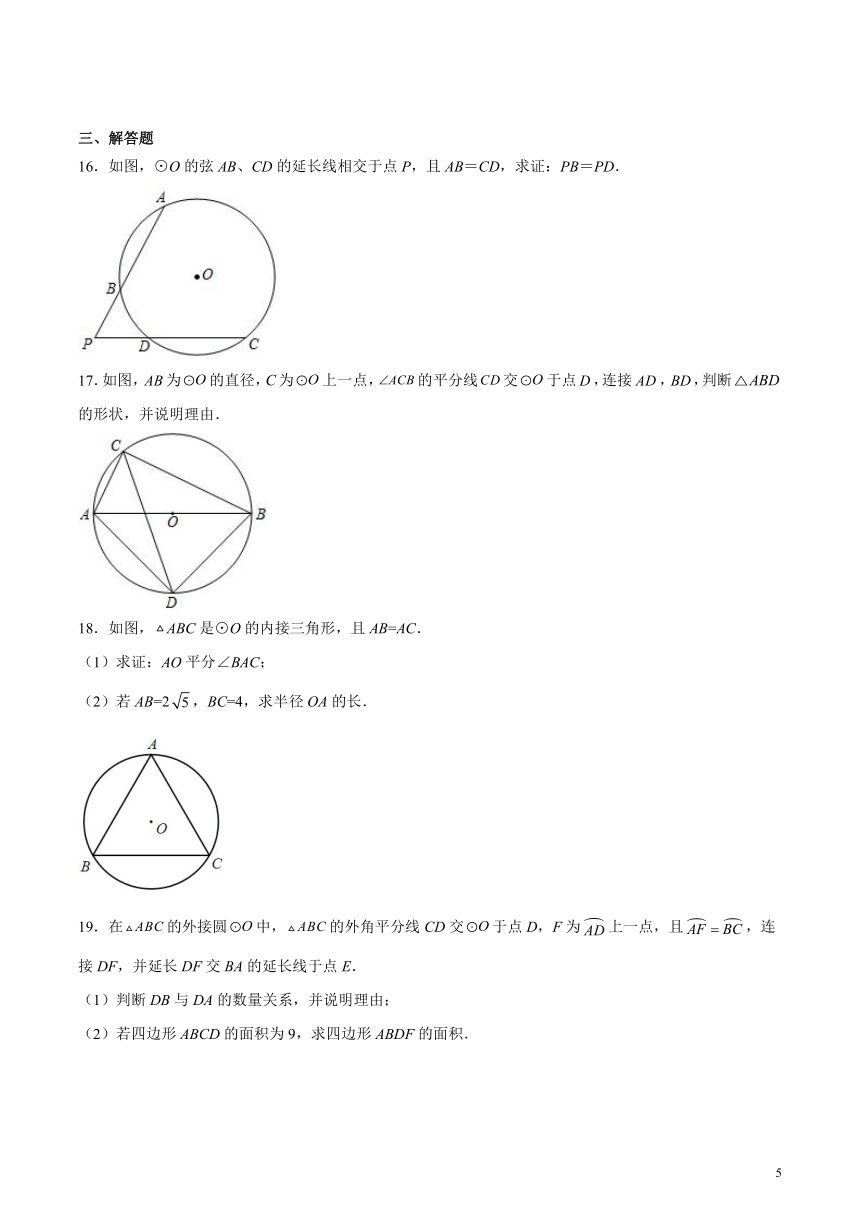
16.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD,求证:PB=PD.
17.如图,为的直径,为上一点,的平分线交于点,连接,,判断的形状,并说明理由.
18.如图,ABC是⊙O的内接三角形,且AB=AC.
(1)求证:AO平分∠BAC;
(2)若AB=2,BC=4,求半径OA的长.
19.在的外接圆中,的外角平分线CD交于点D,F为上一点,且,连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)若四边形ABCD的面积为9,求四边形ABDF的面积.
20.如图,AB是圆O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=8,求圆O的半径.
21.如图,点A和动点P在直线上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ = 90°,AQ : AB = 3 :4,作△ABQ的外接圆O. 点C在点P右侧,PC = 4,过点C作直线⊥,过点O作OD⊥于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF = CD,以DE,DF为邻边作矩形DEGF,设AQ =3 x
(1)用关于的代数式表示BQ,DF;
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,当AP为何值时,矩形DEGF是正方形.
(
2
)
(
1
)
参考答案
1.B2.C3.C4.D5.A6.B7.D8.D9.A10.A
11.140°
12.220
∵
13.
14.54°
15.
16.
证明:连接AC,如图,
∵AB=CD,
∴.
∴.
即.
∴∠A=∠C.
∴PA=PC.
∴PA﹣AB=PC﹣CD.
即:PB=PD.
17
解:△ABD为等腰直角三角形;
理由如下:∵AB为直径,
∴∠ACB=∠ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴,
∴AD=BD,
∴△ABD为等腰直角三角形.
18.
证明:(1)连接、,
在与中,
∵.
,
,
平分;
(2)连接并延长交于,连接,
,平分, BC=4,
,,
∵AB=2,
∴,
设,则,
∵在Rt△OBE中,,
∴
解得:,
半径的长为.
19.
【详解】
(1)平分
(2)
即
四边形ABCD的面积四边形ABDF的面积
四边形ABDF的面积为
20.
(1)证明:,
,
;
(2)连接,设,
,,
,,
在中,
,
解得:,
圆的半径为.
21.
解:(1)在中,
,,
,
,
,,
,
,
,
,
;
(2),,
,
作于点(如图,
,
是的外接圆,,
点是的中点,
,
,
,
,
解得:(舍去),,
;
(3)①若矩形是正方形,则,
.点在点的右侧时(如图
,解得:,
;
.点在点的左侧时,
当点在右侧,
时(如图,
,,
,解得:,
;
当时(如图,
,,
,解得:(舍去),
当点在的左侧时,即(如图,
,,
,解得:,
,
综上所述:当为12或或3时,矩形是正方形;
(
2
)
(
答案第
1
页,共
2
页
)
一、单选题
1.下列说法中,正确的是( )
A.两个半圆是等弧 B.同圆中优弧与半圆的差必是劣弧
C.长度相等的弧是等弧 D.直径未必是弦
2.如图,点,,,在圆上,弦和交于点,则下列说法正确的是( )
A.若平分,则 B.若,则平分
C.若垂直平分,则圆心在上 D.若圆心在上,则垂直平分
3.下列说法:①优弧比劣弧长;②三点可以确定一个圆;③长度相等的弧是等弧;④经过圆内的一个定点可以作无数条弦;其中不正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
5.如图,在⊙O的内接四边形ABCD中,∠BOD=100°,则∠BCD的度数( )
A.130° B.100° C.80° D.50°
6.如图,是圆的直径,点是圆上一点,若,,于点,则的长为( )
A. B.3cm C.5cm D.6cm
7.如图,Rt△ABC的直角顶点C在⊙O上滑动,且各边与⊙O分别交于点D,E,F,G,若,,的度数比为2:3:5,BE=BF,则∠A的度数为( )
A.30° B.32° C.34° D.36°
8.如图,四边形内接于,点P为边AD上任意一点(点P不与点 A 、 重合)连接CP,若,则的度数可能为( )
A.30° B.54° C.50° D.65°
9.如图,AB是⊙O的直径,AB=4,C为半圆O的三等分点(靠近点A),P为⊙O上一动点.若D为AP的中点,则线段CD的最小值为( )
A.-1 B.2 C.+1 D.4
10.如图,函数的图象与x轴交于A,B两点,点C是以为圆心,2为半径的圆上的动点,P是的中点,连结,则线段的最小值是( )
A.1 B. C.2 D.
二、填空题
11.如图,已知四边形是圆的内接四边形,,则______.
12.如图,在的内接五边形中,,,则________.
13.如图,在中,是直径,弦,垂足为E,连接,若,则的半径为_________.
14.如图,CD是⊙O的直径,点A在DC的延长线上,∠A=18°, AE交⊙O于点B,且AB=OD.则∠EOD=______
15.如图,是的直径,,是的半径,,点在上,,点是半径上的一个动点,则的最小值为_______.
三、解答题
16.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD,求证:PB=PD.
17.如图,为的直径,为上一点,的平分线交于点,连接,,判断的形状,并说明理由.
18.如图,ABC是⊙O的内接三角形,且AB=AC.
(1)求证:AO平分∠BAC;
(2)若AB=2,BC=4,求半径OA的长.
19.在的外接圆中,的外角平分线CD交于点D,F为上一点,且,连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)若四边形ABCD的面积为9,求四边形ABDF的面积.
20.如图,AB是圆O的直径,弦CD⊥AB于点E,G是上任意一点,连接AD,AG,GD.
(1)求证:∠ADC=∠AGD;
(2)若BE=2,CD=8,求圆O的半径.
21.如图,点A和动点P在直线上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ = 90°,AQ : AB = 3 :4,作△ABQ的外接圆O. 点C在点P右侧,PC = 4,过点C作直线⊥,过点O作OD⊥于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF = CD,以DE,DF为邻边作矩形DEGF,设AQ =3 x
(1)用关于的代数式表示BQ,DF;
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,当AP为何值时,矩形DEGF是正方形.
(
2
)
(
1
)
参考答案
1.B2.C3.C4.D5.A6.B7.D8.D9.A10.A
11.140°
12.220
∵
13.
14.54°
15.
16.
证明:连接AC,如图,
∵AB=CD,
∴.
∴.
即.
∴∠A=∠C.
∴PA=PC.
∴PA﹣AB=PC﹣CD.
即:PB=PD.
17
解:△ABD为等腰直角三角形;
理由如下:∵AB为直径,
∴∠ACB=∠ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=45°,
∴,
∴AD=BD,
∴△ABD为等腰直角三角形.
18.
证明:(1)连接、,
在与中,
∵.
,
,
平分;
(2)连接并延长交于,连接,
,平分, BC=4,
,,
∵AB=2,
∴,
设,则,
∵在Rt△OBE中,,
∴
解得:,
半径的长为.
19.
【详解】
(1)平分
(2)
即
四边形ABCD的面积四边形ABDF的面积
四边形ABDF的面积为
20.
(1)证明:,
,
;
(2)连接,设,
,,
,,
在中,
,
解得:,
圆的半径为.
21.
解:(1)在中,
,,
,
,
,,
,
,
,
,
;
(2),,
,
作于点(如图,
,
是的外接圆,,
点是的中点,
,
,
,
,
解得:(舍去),,
;
(3)①若矩形是正方形,则,
.点在点的右侧时(如图
,解得:,
;
.点在点的左侧时,
当点在右侧,
时(如图,
,,
,解得:,
;
当时(如图,
,,
,解得:(舍去),
当点在的左侧时,即(如图,
,,
,解得:,
,
综上所述:当为12或或3时,矩形是正方形;
(
2
)
(
答案第
1
页,共
2
页
)
同课章节目录
