2021-2022学年湘教版九年级上册数学第 5 章用样本推断总体 单元检测题A卷(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版九年级上册数学第 5 章用样本推断总体 单元检测题A卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 195.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 19:55:33 | ||
图片预览


文档简介
湘教版九上数学第5章 用样本推断总体 检测试题A卷
(考试时间:120分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.为了解全校学生的身高,在全校1 000名学生中随机抽取了150名学生进行调查.下列说法中正确的是( )
A.总体是全校学生 B.样本容量是1 000
C.个体是每名学生的身高 D.样本是随机抽取的150名学生的上学方式
2.某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个):
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.41 B.42 C.43 D.44
3.质检部门对鑫利会所酒店的餐纸进行调查,随机调查5包(每包5片),5包中合格餐纸分别为4,5,4,5,5,则估计该酒店的餐纸的合格率为( )
A.95% B.92% C.97% D.98%
4.质检部门为了检测某品牌汽车的质量,从同一批次共10万件产品中随机抽取2 000件进行检测,共检测出次品3件,则估计在这一批次的10万产品中次品数约为( )
A.15件 B.30件 C.150件 D.1 500件
5.某中学的八年级(2)班学生对月球上是否有水进行猜想:有35%的人认为有水,45%的人认为无水,20%的人不知道,该校现有八年级学生480人,则认为有水的学生有( )
A.168人 B.216人 C.96人 D.200人
6.甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如下表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
A.甲 B.乙 C.丙 D.丁
队员 平均成绩 方差
甲 9.7 2.12
乙 9.6 0.56
丙 9.7 0.56
丁 9.6 1.34
7.为了了解我市A区和B区期末调考的数学成绩,调查组分别从两区随机各抽查了800份试卷,经过统计计算得到:xA=89,xB=89;s=5.6,s=7.8.由此可以估计A,B两区( )
A.A区的高分比B区多 B.B区学生成绩没有A区学生成绩整齐
C.两区的成绩一样,没有什么差别 D.B区学生成绩比A区学生的成绩整齐
8.为了了解某校九年级学生的运算能力,抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表:
分组 50~59 60~69 70~79 80~89 90~99
频率 0.06 0.16 0.08 0.30 0.40
本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是( )
A.22人 B.30人 C.60人 D.70人
9.某校七年级共有1 000人,为了了解这些学生的视力情况,抽查了20名学生的视力,对所得数据进行整理.若数据在4.85~5.15这一小组的频率为0.3,则可估计该校七年级学生视力在4.85~5.15范围内的人数有( )
A.600人 B.300人 C.150人 D.30人
若一组数据4,,5, ,7, 9 的平均数为6,众数为5,则这组数据的方差为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.在元旦联欢会上,班长准备了若干张相同的卡片,上面写的是联欢会上同学们要回答的问题.联欢会开始后,班长问小明:你能设计一个方案,估计联欢会共准备了多少张卡片吗?小明用20张空白卡片(与写有问题的卡片相同),和全部写有问题的卡片洗匀,从中随机抽取10张,发现有2张空白卡片,马上正确估计出了写有问题卡片的数目,小明估计的数目是 张
12.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 只
13.某市教育局为了解该市2018年九年级学生的身体素质情况,随机抽取了1 000名九年级学生进行检测,身体素质达标率为95%.请你估计该市12万名九年级学生中,身体素质达标的大约有____万人.
14.甲、乙两台机器分别灌装每瓶质量为500克的酸奶,从甲、乙灌装的酸奶中分别随机抽取了30瓶,测得它们实际质量的方差是s=4.8,s=3.6,那么____(填“甲”或“乙”)机器灌装的酸奶质量较稳定.
15.为了解某市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是____(填序号).
①100位女性老人 ②全国内100位老人 ③在城市和乡镇各选10个点,每个点任选10位老人
16.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有____人.
17.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定.根据图中的信息,估计这两人中的新手是____.
第17题图
18.如果一组数据6,7,x,9,5 的平均数是2x,那么这组数据的方差为
三、解答题(共46分)
19.(5分)下表是某居民小区5月份的用水情况:
月用水量(米3) 4 5 6 8 9 11
户数 2 3 7 5 2 1
(1)计算20户家庭的月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计这500户家庭该月共用水多少立方米?
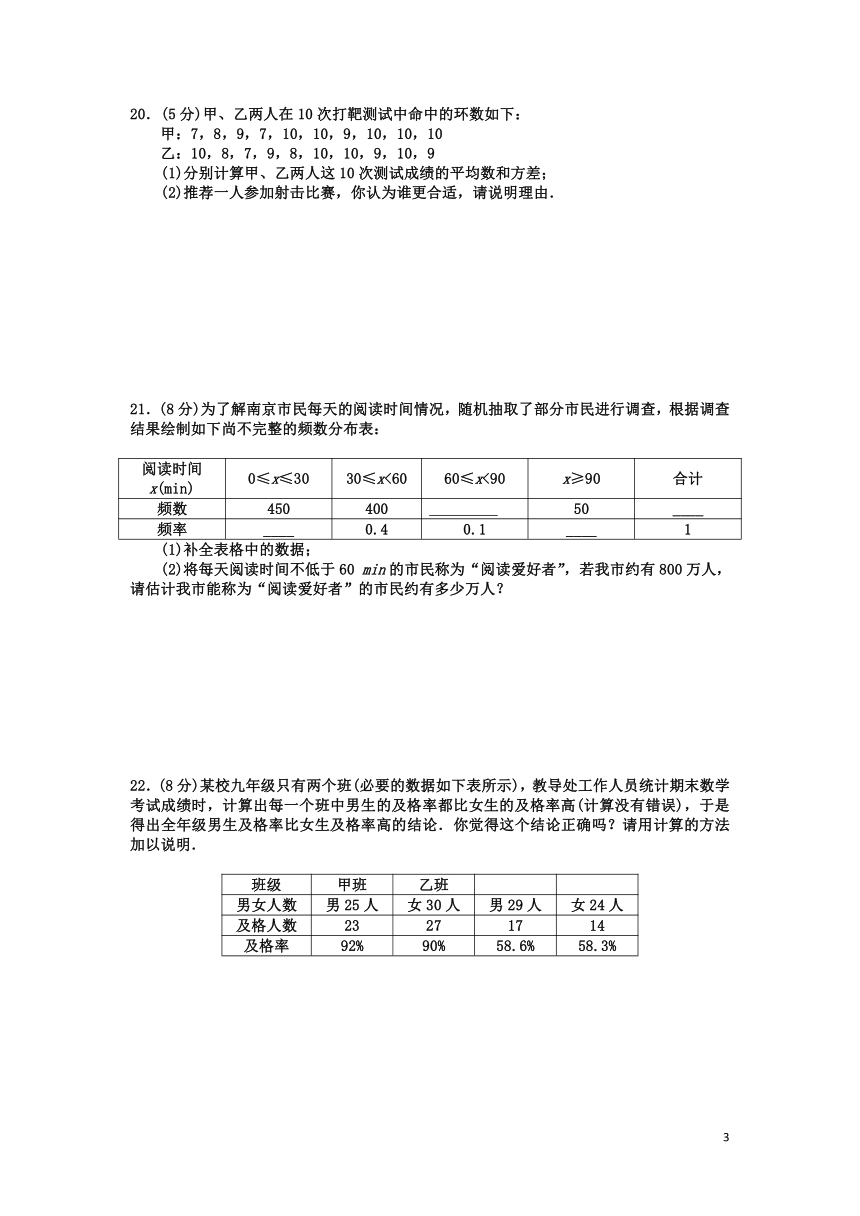
20.(5分)甲、乙两人在10次打靶测试中命中的环数如下:
甲:7,8,9,7,10,10,9,10,10,10
乙:10,8,7,9,8,10,10,9,10,9
(1)分别计算甲、乙两人这10次测试成绩的平均数和方差;
(2)推荐一人参加射击比赛,你认为谁更合适,请说明理由.
21.(8分)为了解南京市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
阅读时间x(min) 0≤x≤30 30≤x<60 60≤x<90 x≥90 合计
频数 450 400 50 ____
频率 ____ 0.4 0.1 ____ 1
(1)补全表格中的数据;
(2)将每天阅读时间不低于60 min的市民称为“阅读爱好者”,若我市约有800万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
22.(8分)某校九年级只有两个班(必要的数据如下表所示),教导处工作人员统计期末数学考试成绩时,计算出每一个班中男生的及格率都比女生的及格率高(计算没有错误),于是得出全年级男生及格率比女生及格率高的结论.你觉得这个结论正确吗?请用计算的方法加以说明.
班级 甲班 乙班
男女人数 男25人 女30人 男29人 女24人
及格人数 23 27 17 14
及格率 92% 90% 58.6% 58.3%
23.(10分)我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的
人数.
24.(10分)某班级要从甲、乙两位同学中选派一人参加“红色故事”演讲比赛.老师对他们的五次模拟演讲比赛成绩(单位:分)进行了整理,计算出甲成绩的平均数是80,甲、乙成绩的方差分别是320,40,但制作的统计图(如图)表尚不完整.
甲、乙两人模拟成绩统计表
第一次 第二次 第三次 第四次 第五次
甲成绩/分 90 100 90 50 a
乙成绩/分 80 70 80 90 80
根据以上信息,请你解答下列问题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中.
答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D B B C A C B D B A
二.填空题
11 12 13 14 15 16 17 18
80 10 000 11.4 乙 ③ 280 小李 4
19.解:(1)20户家庭的月平均用水量为
=6.7立方米.
(2)这500户家庭该月共用水6.7× 500=3 350立方米.
20.解:(1)x甲=9分,s=1.4;x乙=9分;x=1;
(2)∵x甲=x乙,s>s,可推测乙的成绩更稳定,
∴应推荐乙去参赛.
21.(1)补全表格中的数据;
阅读时间x(min) 0≤x≤30 30≤x<60 60≤x<90 x≥90 合计
频数 450 400 __100__ 50 __1__000__
频率 __0.45__ 0.4 0.1 __0.05__ 1
(2)解:根据题意得800×(0.1+0.05)=120万人.
答:估计我市能称为“阅读爱好者”的市民约有120万人.
22.解:结论错误,男生的及格率为
× 100%=× 100%.
女生的及格率为× 100%=× 100%.
∴全年级男生及格率<全年级女生及格率.
23.解:解:(1)120
(2)54°
(3)补全条形统计图如下.
(4)×800=200(人).
答:对食品安全知识“非常了解”的学生约200人.
24.(1)70
(2)如答图所示.
第16题答图
(3)乙=×(80+70+80+90+80)=80.
(4)因为甲、乙成绩的平均数相同,乙成绩的方差小于甲成绩的方差,
所以乙的成绩比甲的成绩稳定.
所以乙将被选中.
(考试时间:120分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.为了解全校学生的身高,在全校1 000名学生中随机抽取了150名学生进行调查.下列说法中正确的是( )
A.总体是全校学生 B.样本容量是1 000
C.个体是每名学生的身高 D.样本是随机抽取的150名学生的上学方式
2.某中学九年级二班六组的8名同学在一次排球垫球测试中的成绩如下(单位:个):
35 38 42 44 40 47 45 45
则这组数据的中位数、平均数分别是( )
A.41 B.42 C.43 D.44
3.质检部门对鑫利会所酒店的餐纸进行调查,随机调查5包(每包5片),5包中合格餐纸分别为4,5,4,5,5,则估计该酒店的餐纸的合格率为( )
A.95% B.92% C.97% D.98%
4.质检部门为了检测某品牌汽车的质量,从同一批次共10万件产品中随机抽取2 000件进行检测,共检测出次品3件,则估计在这一批次的10万产品中次品数约为( )
A.15件 B.30件 C.150件 D.1 500件
5.某中学的八年级(2)班学生对月球上是否有水进行猜想:有35%的人认为有水,45%的人认为无水,20%的人不知道,该校现有八年级学生480人,则认为有水的学生有( )
A.168人 B.216人 C.96人 D.200人
6.甲、乙、丙、丁四名射击队员考核赛的平均成绩(环)及方差统计如下表,现要根据这些数据,从中选出一人参加比赛,如果你是教练员,你的选择是( )
A.甲 B.乙 C.丙 D.丁
队员 平均成绩 方差
甲 9.7 2.12
乙 9.6 0.56
丙 9.7 0.56
丁 9.6 1.34
7.为了了解我市A区和B区期末调考的数学成绩,调查组分别从两区随机各抽查了800份试卷,经过统计计算得到:xA=89,xB=89;s=5.6,s=7.8.由此可以估计A,B两区( )
A.A区的高分比B区多 B.B区学生成绩没有A区学生成绩整齐
C.两区的成绩一样,没有什么差别 D.B区学生成绩比A区学生的成绩整齐
8.为了了解某校九年级学生的运算能力,抽取了100名学生进行测试,将所得成绩(单位:分)整理后,列出下表:
分组 50~59 60~69 70~79 80~89 90~99
频率 0.06 0.16 0.08 0.30 0.40
本次测试这100名学生成绩良好(大于或等于80分为良好)的人数是( )
A.22人 B.30人 C.60人 D.70人
9.某校七年级共有1 000人,为了了解这些学生的视力情况,抽查了20名学生的视力,对所得数据进行整理.若数据在4.85~5.15这一小组的频率为0.3,则可估计该校七年级学生视力在4.85~5.15范围内的人数有( )
A.600人 B.300人 C.150人 D.30人
若一组数据4,,5, ,7, 9 的平均数为6,众数为5,则这组数据的方差为( )
A. B. C. D.
二、填空题(每小题3分,共24分)
11.在元旦联欢会上,班长准备了若干张相同的卡片,上面写的是联欢会上同学们要回答的问题.联欢会开始后,班长问小明:你能设计一个方案,估计联欢会共准备了多少张卡片吗?小明用20张空白卡片(与写有问题的卡片相同),和全部写有问题的卡片洗匀,从中随机抽取10张,发现有2张空白卡片,马上正确估计出了写有问题卡片的数目,小明估计的数目是 张
12.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为 只
13.某市教育局为了解该市2018年九年级学生的身体素质情况,随机抽取了1 000名九年级学生进行检测,身体素质达标率为95%.请你估计该市12万名九年级学生中,身体素质达标的大约有____万人.
14.甲、乙两台机器分别灌装每瓶质量为500克的酸奶,从甲、乙灌装的酸奶中分别随机抽取了30瓶,测得它们实际质量的方差是s=4.8,s=3.6,那么____(填“甲”或“乙”)机器灌装的酸奶质量较稳定.
15.为了解某市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是____(填序号).
①100位女性老人 ②全国内100位老人 ③在城市和乡镇各选10个点,每个点任选10位老人
16.如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有____人.
17.小李和小林练习射箭,射完10箭后两人的成绩如图所示,通常新手的成绩不太稳定.根据图中的信息,估计这两人中的新手是____.
第17题图
18.如果一组数据6,7,x,9,5 的平均数是2x,那么这组数据的方差为
三、解答题(共46分)
19.(5分)下表是某居民小区5月份的用水情况:
月用水量(米3) 4 5 6 8 9 11
户数 2 3 7 5 2 1
(1)计算20户家庭的月平均用水量;
(2)如果该小区有500户家庭,根据上面的计算结果,估计这500户家庭该月共用水多少立方米?
20.(5分)甲、乙两人在10次打靶测试中命中的环数如下:
甲:7,8,9,7,10,10,9,10,10,10
乙:10,8,7,9,8,10,10,9,10,9
(1)分别计算甲、乙两人这10次测试成绩的平均数和方差;
(2)推荐一人参加射击比赛,你认为谁更合适,请说明理由.
21.(8分)为了解南京市民每天的阅读时间情况,随机抽取了部分市民进行调查,根据调查结果绘制如下尚不完整的频数分布表:
阅读时间x(min) 0≤x≤30 30≤x<60 60≤x<90 x≥90 合计
频数 450 400 50 ____
频率 ____ 0.4 0.1 ____ 1
(1)补全表格中的数据;
(2)将每天阅读时间不低于60 min的市民称为“阅读爱好者”,若我市约有800万人,请估计我市能称为“阅读爱好者”的市民约有多少万人?
22.(8分)某校九年级只有两个班(必要的数据如下表所示),教导处工作人员统计期末数学考试成绩时,计算出每一个班中男生的及格率都比女生的及格率高(计算没有错误),于是得出全年级男生及格率比女生及格率高的结论.你觉得这个结论正确吗?请用计算的方法加以说明.
班级 甲班 乙班
男女人数 男25人 女30人 男29人 女24人
及格人数 23 27 17 14
及格率 92% 90% 58.6% 58.3%
23.(10分)我市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校随机抽取了部分学生进行问卷调查,将调查结果按照“A非常了解、B了解、C了解较少、D不了解”四类分别进行统计,并绘制了下列两幅统计图(不完整).请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)扇形统计图中D所在扇形的圆心角为 ;
(3)将上面的条形统计图补充完整;
(4)若该校共有800名学生,请你估计对食品安全知识“非常了解”的学生的
人数.
24.(10分)某班级要从甲、乙两位同学中选派一人参加“红色故事”演讲比赛.老师对他们的五次模拟演讲比赛成绩(单位:分)进行了整理,计算出甲成绩的平均数是80,甲、乙成绩的方差分别是320,40,但制作的统计图(如图)表尚不完整.
甲、乙两人模拟成绩统计表
第一次 第二次 第三次 第四次 第五次
甲成绩/分 90 100 90 50 a
乙成绩/分 80 70 80 90 80
根据以上信息,请你解答下列问题:
(1)a= ;
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中.
答案
一、选择题
1 2 3 4 5 6 7 8 9 10
D B B C A C B D B A
二.填空题
11 12 13 14 15 16 17 18
80 10 000 11.4 乙 ③ 280 小李 4
19.解:(1)20户家庭的月平均用水量为
=6.7立方米.
(2)这500户家庭该月共用水6.7× 500=3 350立方米.
20.解:(1)x甲=9分,s=1.4;x乙=9分;x=1;
(2)∵x甲=x乙,s>s,可推测乙的成绩更稳定,
∴应推荐乙去参赛.
21.(1)补全表格中的数据;
阅读时间x(min) 0≤x≤30 30≤x<60 60≤x<90 x≥90 合计
频数 450 400 __100__ 50 __1__000__
频率 __0.45__ 0.4 0.1 __0.05__ 1
(2)解:根据题意得800×(0.1+0.05)=120万人.
答:估计我市能称为“阅读爱好者”的市民约有120万人.
22.解:结论错误,男生的及格率为
× 100%=× 100%.
女生的及格率为× 100%=× 100%.
∴全年级男生及格率<全年级女生及格率.
23.解:解:(1)120
(2)54°
(3)补全条形统计图如下.
(4)×800=200(人).
答:对食品安全知识“非常了解”的学生约200人.
24.(1)70
(2)如答图所示.
第16题答图
(3)乙=×(80+70+80+90+80)=80.
(4)因为甲、乙成绩的平均数相同,乙成绩的方差小于甲成绩的方差,
所以乙的成绩比甲的成绩稳定.
所以乙将被选中.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
