第23章 旋转 单元测试题 2021—2022学年人教版数学九年级上册(word版含答案)
文档属性
| 名称 | 第23章 旋转 单元测试题 2021—2022学年人教版数学九年级上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 643.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 21:11:50 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学上册 第二十三章 旋转 单元测试题
一、选择题(30分)
1.下列图片中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列图形既是中心对称又是轴对称的是( )
A. B. C. D.
3.如图,在中,,D,E是斜边BC上两点,且,将绕点A顺时针旋转90°后,得到,连接EF,下列结论:①;②;③;④.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
4.如图,在RtABC中,∠ABC=90°,AB=BC,点P在ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP=6,则PC的最小值是( )
A.2 B.3 C.3-3 D.3
5.△ABC是等边三角形,点P在△ABC内,PA=4,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )
A.4 B. C.2 D.
6.如图,在中,,D为内一点,,连接,将绕点A按逆时针方向旋转,使与重合,点D的对应点为点E,连接,交于点F,则的长为( )
A. B. C. D.
7.如图,矩形ABCD的边CD上有一点E,∠DAE=22.5°,EF⊥AB,垂足为F,将△AEF绕着点F顺时针旋转,使得点A的对应点M落在EF上,点E恰好落在点B处,连接BE.下列结论:①BM⊥AE;②四边形EFBC是正方形;③∠EBM=30°;④.其中结论正确的序号是( )
A.①② B.①②③ C.①②④ D.③④
8.如图,△AOB中,OA=4,OB=6,AB=2,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(4,2)或(﹣4,2) B.(2,﹣4)或(﹣2,4)
C.(﹣2,2)或(2,﹣2) D.(2,﹣2)或(﹣2,2)
9.在平面直角坐标系中,将等腰直角三角形按如图所示的位置放置,然后绕原点逆时针旋转到的位置,若点的坐标为,则点的坐标为( )
A. B. C. D.
10.如图,将正方形绕点逆时针旋转得到.如果,点与的距离为( )
A. B. C. D.
二、填空题(15分)
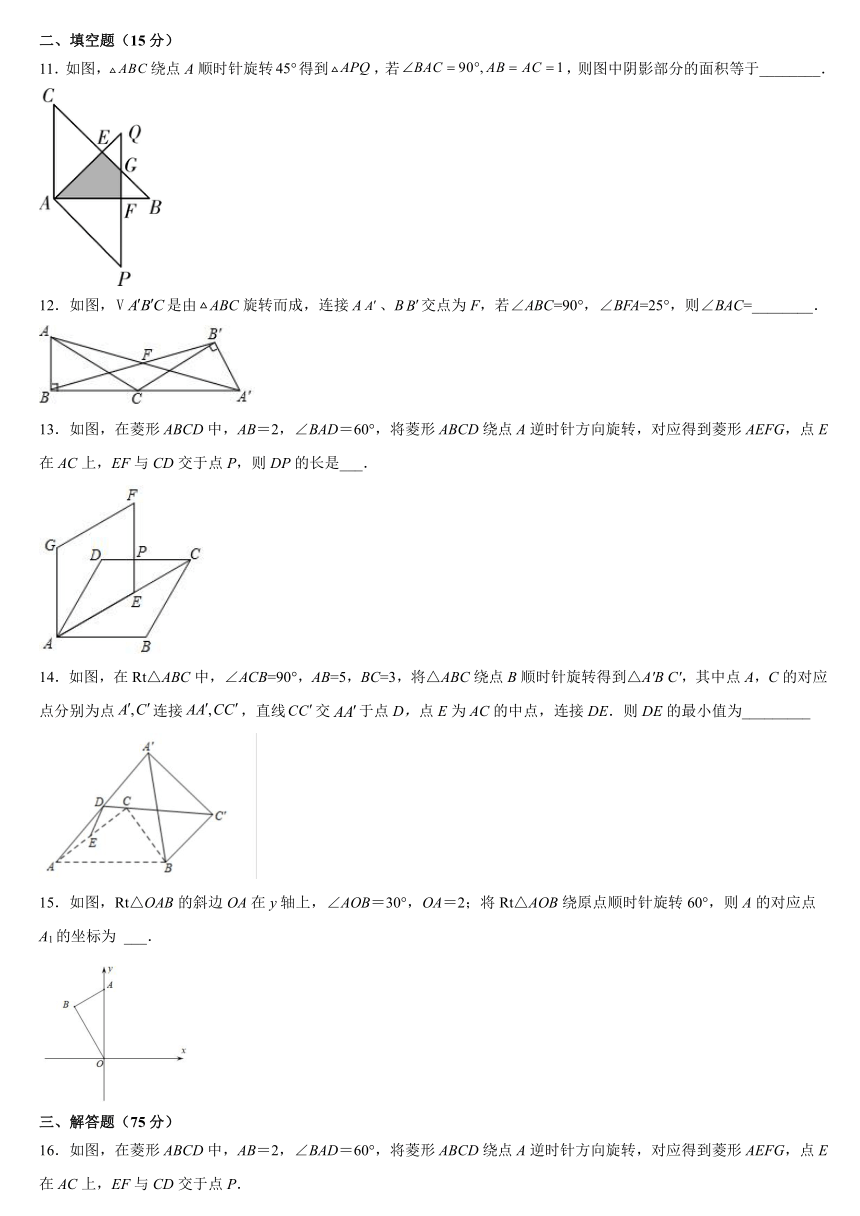
11.如图,绕点A顺时针旋转得到,若,则图中阴影部分的面积等于________.
12.如图,是由ABC旋转而成,连接A、B交点为F,若∠ABC=90°,∠BFA=25°,则∠BAC=________.
13.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是___.
14.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′B C′,其中点A,C的对应点分别为点连接,直线交于点D,点E为AC的中点,连接DE.则DE的最小值为_________
15.如图,Rt△OAB的斜边OA在y轴上,∠AOB=30°,OA=2;将Rt△AOB绕原点顺时针旋转60°,则A的对应点A1的坐标为 ___.
三、解答题(75分)
16.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P.
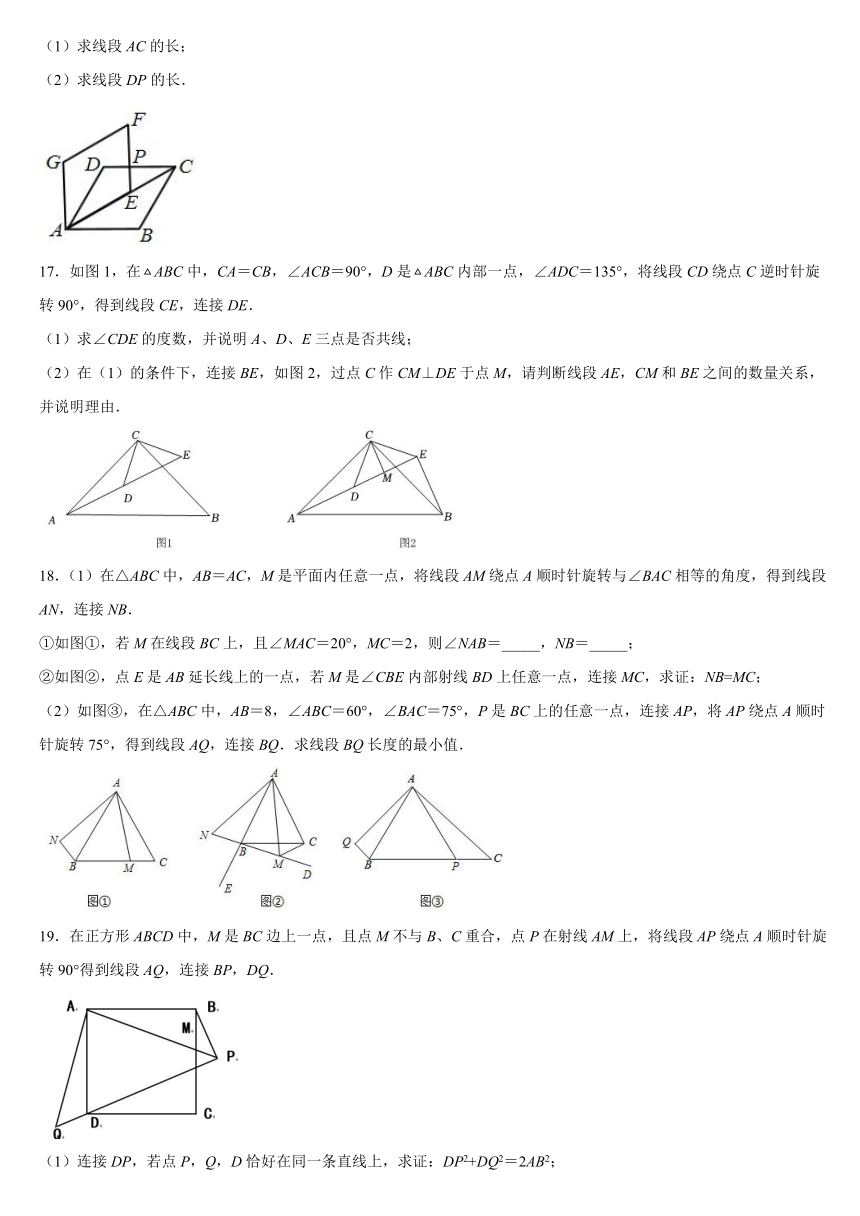
(1)求线段AC的长;
(2)求线段DP的长.
17.如图1,在ABC中,CA=CB,∠ACB=90°,D是ABC内部一点,∠ADC=135°,将线段CD绕点C逆时针旋转90°,得到线段CE,连接DE.
(1)求∠CDE的度数,并说明A、D、E三点是否共线;
(2)在(1)的条件下,连接BE,如图2,过点C作CM⊥DE于点M,请判断线段AE,CM和BE之间的数量关系,并说明理由.
18.(1)在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A顺时针旋转与∠BAC相等的角度,得到线段AN,连接NB.
①如图①,若M在线段BC上,且∠MAC=20°,MC=2,则∠NAB=_____,NB=_____;
②如图②,点E是AB延长线上的一点,若M是∠CBE内部射线BD上任意一点,连接MC,求证:NB=MC;
(2)如图③,在△ABC中,AB=8,∠ABC=60°,∠BAC=75°,P是BC上的任意一点,连接AP,将AP绕点A顺时针旋转75°,得到线段AQ,连接BQ.求线段BQ长度的最小值.
19.在正方形ABCD中,M是BC边上一点,且点M不与B、C重合,点P在射线AM上,将线段AP绕点A顺时针旋转90°得到线段AQ,连接BP,DQ.
(1)连接DP,若点P,Q,D恰好在同一条直线上,求证:DP2+DQ2=2AB2;
(2)若点P,Q,C恰好在同一条直线上,求证:BP=AB .
20.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点E,F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),过点A作AG⊥AH且AG=AH,连接GC,HB.
(1)证明:AHB≌AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①证明:在点H的运动过程中,总有∠HFG=90°;
②当AQG为等腰三角形时,求∠AHE的度数.
21.如图(1)正方形ABCD和正方形AEFG,边AE在边AB上,AB=6,AE=3.将正方形AEFG绕点A逆时针旋转α(0°≤α≤45°).
(1)当正方形AEFG旋转到如图(2)的位置时,求证:BE=DG;
(2)BE的延长线交直线DG于点Q,当BF=BC时,
①求证:直线BE是AF的垂直平分线;
②求线段DG的长.
22.如图,等腰Rt△ABC,AB=AC,∠BAC=90°,直线AB绕点A旋转,得直线AP,点B关于直线AP的对称点为E,连接AE,CE,CE交直线AP于点F,连接BF.
(1)连接BE,求∠BEC度数.
(2)①如图1,猜想线段FE,FA,FC之间的数量关系,并说明理由;
②当直线AP旋转到如图2位置时,(1)中结论是否成立?若成立,请说明理由;若不成立,请直接写出正确的结论,不用说明理由;
(3)若AC=2,当∠BAP=30°时,求线段CE的长.
23.综合与实践
已知是等腰三角形,.
(1)特殊情形:如图1,当∥时,______.(填“>”“<”或“=”)
(2)发现结论:若将图1中的绕点顺时针旋转()到图2所示的位置,则(1)中的结论还成立吗?请说明理由.
(3)拓展运用:某学习小组在解答问题:“如图3,点是等腰直角三角形内一点,,且,,,求的度数”时,小明发现可以利用旋转的知识,将绕点顺时针旋转90°得到,连接,构造新图形解决问题.请你根据小明的发现直接写出的度数.
【参考答案】
1.B 2.C 3.B 4.D 5.A 6.A 7.C 8.C 9.C 10.D
11.
12.75°
13.
14.1
15.
16.解:(1)连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,
∴OB=AB=1,
∴OA=OB=,
∴AC=2,
(2)由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC AE=2 2,
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE=CE= 1,PC=PE=3 ,
∴DP=CD PC=2 (3 )= 1.
17.解:(1)∵将线段CD绕点C逆时针旋转90°,
∴CD=CE,∠DCE=90°,
∴∠CDE=45°,
∵∠ADC=135°,
∴∠ADC+∠CDE=180°,
∴A、D、E三点共线;
(2)AE=BE+2CM,理由如下:
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴BE=AD,
∵CD=CE,∠DCE=90°,CM⊥DE,
∴DE=2CM,
∴AE=AD+DE=BE+2CM.
18.(1)①∵线段AM绕点A顺时针旋转与∠BAC相等的角度,
∴,,
∴,
∴,
∴在△NAB和△MAC中,
,
∴△NAB≌△MAC(SAS),
∴;
②证明:∵∠NAM=∠BAC,
∴,
∴∠NAB=∠MAC,
在△NAB和△MAC中,
,
∴△NAB≌△MAC(SAS),
∴NB=CM,
(2)如图:在AC上取一点E,使AE=AB=8,连接PE,过点E作EF⊥BC于F,过A作AD⊥BC于D,
∵∠PAQ=∠CAB,
∴∠CAP=∠BAQ,
在△BAQ和△EAP中,
,
∴△BAQ≌△EAP(SAS),
∴BQ=EP,
要使BQ最小,则有EP最小,而点E是定点,点P是BC上的动点,
∴当EP⊥BC(点P和点F重合)时,EP最小,
即:点P与点F重合,BQ最小,最小值为EF,
∵AB=8,∠ABC=60°,
∴,
∴BD=,AD=,
∵∠BAC=75°,
∴,
∴是等腰直角三角形,
∴,
∴AC,
∴EC,
又∵∠C=45°,
∴是等腰直角三角形,
∴,
∵,
∴,
∴EF=,
故线段BQ长度最小值是.
19.解:(1)连接BD,如图2,
∵线段AP绕点A顺时针旋转90°得到线段AQ,
∴AQ=AP,∠QAP=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠1+∠DAP=∠2+∠DAP=90°。
∴∠1=∠2,
∴△ADQ≌△ABP(SAS),
∴DQ=BP,∠Q=∠3,
∵在Rt△QAP中,∠Q+∠QPA=90°,
∴∠BPD=∠3+∠QPA=90°,
∵在Rt△BPD中,DP2+BP2=BD2,
又∵DQ=BP,BD2=AB2+AD2=2AB2,
∴DP2+DQ2=2AB2;
(2)结论:BP=AB.
理由:如图3中,连接AC,延长CD到N,使得DN=CD,连接AN,QN.
∵AQ=AP,∠QAP=90°,
∴∠AQP=∠APQ=45°,
∵ND=CD,AD⊥NC,
∴AN=AC,
∵四边形ABCD是正方形,
∴∠ANC=∠CAN=45°,
∴∠NAC=90°,
∴∠NAQ+∠QAC=∠QAC+∠PAC=90°,
∴∠NAQ=∠CAP,
又∵AN=AC,AQ=AP,
∴△ANQ≌△ACP(SAS),
同(1)可知△ADQ≌△ABP,
∴DQ=PB,∠AQN=∠APC=45°,
∵∠AQP=45°,
∴∠NQC=90°,
∵CD=DN,
∴D是CN的中点,
∴DQ=CD=DN=AB,
∴PB=AB.
20.(1)证明:如图1,
由旋转得:AH=AG,∠HAG=90°,
∵∠BAC=90°,
∴∠BAH=∠CAG,
∵AB=AC,
∴△ABH≌△ACG(SAS);
(2)①证明:如图2,在等腰直角三角形ABC中,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵点E,F分别为AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,AE=AB,AF=AC,
∴AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,
∵∠EAH=∠FAG,AH=AG,
∴△AEH≌△AFG(SAS),
∴∠AFG=∠AEH=45°,
∴∠HFG=45°+45°=90°;
②分两种情况:
i)如图3,AQ=QG时,
∵AQ=QG,
∴∠QAG=∠AGQ,
∵AG⊥AH且AG=AH,
∴∠AHG=∠AGH=45°,
∴∠AHG=∠AGH=∠HAQ=∠QAG=45°,
∴∠EAH=∠FAH=45°,
∵AE=AF,AH=AH,
∴△AEH≌△AFH(SAS),
∴∠AHE=∠AHF,
∵∠AHE+∠AHF=180°,
∴∠AHE=∠AHF=90°;
ii)如图4,当AG=QG时,∠GAQ=∠AQG,
∵∠AEH=∠AGQ=45°,
∴∠GAQ=∠AQG==67.5°,
∵∠EAQ=∠HAG=90°,
∴∠EAH=∠GAQ=67.5°,
∴∠AHE=∠AQG=67.5°;
∵H为线段EF上一动点(不与点E,F重合),
∴不存在AG=AQ的情况.
综上,当△AQG为等腰三角形时,∠AHE的度数为67.5°或90°.
21.(1)证明:在正方形ABCD和正方形AEFG中,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∵∠BAE+∠EAD=∠BAD=90°,∠DAG+∠EAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),
∴BE=DG;
(2)①在正方形ABCD和正方形AEFG中,
∴AB=BC,AE=EF,
∵BF=BC,
∴BF=BA,
∴直线BE是AF的垂直平分线;
②∵直线BE是AF的垂直平分线,
∴QF=QA,
∵正方形AEFG中,
∴GF=GA,
∴点G与点Q重合,
正方形AEFG中,AE=3.
∴OA=OE=3,
在Rt△BOA中,,即,
∴OB=3,
由(1)得BE=DG,
∴DG=BE=OB-OE=.
22.解:(1)如图,设AB交CE于点O,
∵点B关于直线AP的对称点为E,
∴AE=AB,∠E=∠ABF,∠AFE=∠AFB,EF=BF,
∵AB=AC,
∴AE=AC,
∴∠E=∠ACE,
∴∠ABF=∠ACE,
∵∠AOC=∠BOF,
∵∠BAC=90°,
∴∠BFO=∠BFE=∠OAC=90°,
∴ ;
(2)①,理由如下:
如图,过点A作AT⊥AF交EC于点T,设AB交CE于点O,
由(1)得:∠BFO=∠OAC=90°,
∴ ,
∴∠AFT=∠AFB-∠BFO=45°,
∵AT⊥AF,
∴∠FAT=90°,
∴∠ATF=45°,
∴∠AFT=∠ATF,
∴AF=AT,
∵ ,
∴ ,
∵∠BAC=∠FAT=90°,
∴∠FAB=∠TAC,
在△FAB和△TAC中,
∵AF=AT,∠FAB=∠TAC,AB=AC,
∴△FAB≌△TAC(SAS),
∴BF=CT,
∵EF=BF,
∴EF=CT,
∴CF-EF=CF-CT=FT= ,
即 ;
②(1)中结论不成立,,理由如下:
如图,过点A作AH⊥AF交EC于点H,设AB交CE于点O,
∵点B关于直线AP的对称点为E,
∴AE=AB,∠E=∠ABF,∠AFE=∠AFB,EF=BF,
∵AB=AC,
∴AE=AC,
∴∠E=∠ACE,
∴∠ABF=∠ACE,
∵∠AOB=∠COF,
∴∠BFC=∠OAB=90°,
∴ ,
∵AH⊥AF,
∴∠FAH=90°,
∴∠AHF=∠AFH=45°,
∴AF=AH,
∵ ,
∴ ,
∵∠BAC=∠FAH=90°,
∴∠FAB=∠HAC,
在△FAB和△HAC中,
∵AF=AH,∠FAB=∠HAC,AB=AC,
∴△FAB≌△HAC(SAS),
∴BF=CH,
∵EF=BF,
∴EF=CH,
∴ ,
即 ;
(3)如图,过点C作CR⊥AE交EA的延长线于点R,
∵∠PAB=∠PAE=30°,
∴∠BAE=60°,
∴∠CAE=∠CAB+∠BAE=90°+60°=150°,
∴∠CAR=180°-150°=30°,
∵CR⊥AR,AC=2,
∴ ,
∴ ,
由(1)知:AE=AC=2,
∴ ,
∴ ,
如图,过点C作CS⊥AE交EA的延长线于点S,
∵∠PAB=∠PAE=30°,∠BAC=90°,
∴∠CAE=90°-30°-30°=30°,
∵AE=AAC=2,
∴ ,
∴ ,
∴ ,
∴ ,
综上所述,EC的长为 或.
23.解:(1)∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
故答案为:=;
(2)成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,
∴△DAB≌△EAC(SAS),
∴DB=CE;
(3)如图,
将△APB绕点A旋转90°得△AEC,连接PE,
∴△APB≌△AEC,
∴AE=AP=2,EC=BP=1,∠PAE=90°,
∴∠AEP=∠APE=45°,
在Rt△PAE中,由勾股定理可得,PE=2,
在△PEC中,PE2=(2)2=8,CE2=12=1,PC2=32=9,
∵PE2+CE2=PA2,
∴△PEC是直角三角形,
∴∠PEC=90°,
∴∠AEC=135°,
又∵△APB≌△AEC,
∴∠BPA=∠CEA=135°
一、选择题(30分)
1.下列图片中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下列图形既是中心对称又是轴对称的是( )
A. B. C. D.
3.如图,在中,,D,E是斜边BC上两点,且,将绕点A顺时针旋转90°后,得到,连接EF,下列结论:①;②;③;④.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
4.如图,在RtABC中,∠ABC=90°,AB=BC,点P在ABC内一点,连接PA,PB,PC,若∠BAP=∠CBP,且AP=6,则PC的最小值是( )
A.2 B.3 C.3-3 D.3
5.△ABC是等边三角形,点P在△ABC内,PA=4,将△PAB绕点A逆时针旋转得到△P1AC,则P1P的长等于( )
A.4 B. C.2 D.
6.如图,在中,,D为内一点,,连接,将绕点A按逆时针方向旋转,使与重合,点D的对应点为点E,连接,交于点F,则的长为( )
A. B. C. D.
7.如图,矩形ABCD的边CD上有一点E,∠DAE=22.5°,EF⊥AB,垂足为F,将△AEF绕着点F顺时针旋转,使得点A的对应点M落在EF上,点E恰好落在点B处,连接BE.下列结论:①BM⊥AE;②四边形EFBC是正方形;③∠EBM=30°;④.其中结论正确的序号是( )
A.①② B.①②③ C.①②④ D.③④
8.如图,△AOB中,OA=4,OB=6,AB=2,将△AOB绕原点O旋转90°,则旋转后点A的对应点A′的坐标是( )
A.(4,2)或(﹣4,2) B.(2,﹣4)或(﹣2,4)
C.(﹣2,2)或(2,﹣2) D.(2,﹣2)或(﹣2,2)
9.在平面直角坐标系中,将等腰直角三角形按如图所示的位置放置,然后绕原点逆时针旋转到的位置,若点的坐标为,则点的坐标为( )
A. B. C. D.
10.如图,将正方形绕点逆时针旋转得到.如果,点与的距离为( )
A. B. C. D.
二、填空题(15分)
11.如图,绕点A顺时针旋转得到,若,则图中阴影部分的面积等于________.
12.如图,是由ABC旋转而成,连接A、B交点为F,若∠ABC=90°,∠BFA=25°,则∠BAC=________.
13.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P,则DP的长是___.
14.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,将△ABC绕点B顺时针旋转得到△A′B C′,其中点A,C的对应点分别为点连接,直线交于点D,点E为AC的中点,连接DE.则DE的最小值为_________
15.如图,Rt△OAB的斜边OA在y轴上,∠AOB=30°,OA=2;将Rt△AOB绕原点顺时针旋转60°,则A的对应点A1的坐标为 ___.
三、解答题(75分)
16.如图,在菱形ABCD中,AB=2,∠BAD=60°,将菱形ABCD绕点A逆时针方向旋转,对应得到菱形AEFG,点E在AC上,EF与CD交于点P.
(1)求线段AC的长;
(2)求线段DP的长.
17.如图1,在ABC中,CA=CB,∠ACB=90°,D是ABC内部一点,∠ADC=135°,将线段CD绕点C逆时针旋转90°,得到线段CE,连接DE.
(1)求∠CDE的度数,并说明A、D、E三点是否共线;
(2)在(1)的条件下,连接BE,如图2,过点C作CM⊥DE于点M,请判断线段AE,CM和BE之间的数量关系,并说明理由.
18.(1)在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A顺时针旋转与∠BAC相等的角度,得到线段AN,连接NB.
①如图①,若M在线段BC上,且∠MAC=20°,MC=2,则∠NAB=_____,NB=_____;
②如图②,点E是AB延长线上的一点,若M是∠CBE内部射线BD上任意一点,连接MC,求证:NB=MC;
(2)如图③,在△ABC中,AB=8,∠ABC=60°,∠BAC=75°,P是BC上的任意一点,连接AP,将AP绕点A顺时针旋转75°,得到线段AQ,连接BQ.求线段BQ长度的最小值.
19.在正方形ABCD中,M是BC边上一点,且点M不与B、C重合,点P在射线AM上,将线段AP绕点A顺时针旋转90°得到线段AQ,连接BP,DQ.
(1)连接DP,若点P,Q,D恰好在同一条直线上,求证:DP2+DQ2=2AB2;
(2)若点P,Q,C恰好在同一条直线上,求证:BP=AB .
20.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点E,F分别为AB,AC的中点,H为线段EF上一动点(不与点E,F重合),过点A作AG⊥AH且AG=AH,连接GC,HB.
(1)证明:AHB≌AGC;
(2)如图2,连接GF,HG,HG交AF于点Q.
①证明:在点H的运动过程中,总有∠HFG=90°;
②当AQG为等腰三角形时,求∠AHE的度数.
21.如图(1)正方形ABCD和正方形AEFG,边AE在边AB上,AB=6,AE=3.将正方形AEFG绕点A逆时针旋转α(0°≤α≤45°).
(1)当正方形AEFG旋转到如图(2)的位置时,求证:BE=DG;
(2)BE的延长线交直线DG于点Q,当BF=BC时,
①求证:直线BE是AF的垂直平分线;
②求线段DG的长.
22.如图,等腰Rt△ABC,AB=AC,∠BAC=90°,直线AB绕点A旋转,得直线AP,点B关于直线AP的对称点为E,连接AE,CE,CE交直线AP于点F,连接BF.
(1)连接BE,求∠BEC度数.
(2)①如图1,猜想线段FE,FA,FC之间的数量关系,并说明理由;
②当直线AP旋转到如图2位置时,(1)中结论是否成立?若成立,请说明理由;若不成立,请直接写出正确的结论,不用说明理由;
(3)若AC=2,当∠BAP=30°时,求线段CE的长.
23.综合与实践
已知是等腰三角形,.
(1)特殊情形:如图1,当∥时,______.(填“>”“<”或“=”)
(2)发现结论:若将图1中的绕点顺时针旋转()到图2所示的位置,则(1)中的结论还成立吗?请说明理由.
(3)拓展运用:某学习小组在解答问题:“如图3,点是等腰直角三角形内一点,,且,,,求的度数”时,小明发现可以利用旋转的知识,将绕点顺时针旋转90°得到,连接,构造新图形解决问题.请你根据小明的发现直接写出的度数.
【参考答案】
1.B 2.C 3.B 4.D 5.A 6.A 7.C 8.C 9.C 10.D
11.
12.75°
13.
14.1
15.
16.解:(1)连接BD交AC于O,如图所示:
∵四边形ABCD是菱形,
∴CD=AB=2,∠BCD=∠BAD=60°,∠ACD=∠BAC=∠BAD=30°,OA=OC,AC⊥BD,
∴OB=AB=1,
∴OA=OB=,
∴AC=2,
(2)由旋转的性质得:AE=AB=2,∠EAG=∠BAD=60°,
∴CE=AC AE=2 2,
∵四边形AEFG是菱形,
∴EF∥AG,
∴∠CEP=∠EAG=60°,
∴∠CEP+∠ACD=90°,
∴∠CPE=90°,
∴PE=CE= 1,PC=PE=3 ,
∴DP=CD PC=2 (3 )= 1.
17.解:(1)∵将线段CD绕点C逆时针旋转90°,
∴CD=CE,∠DCE=90°,
∴∠CDE=45°,
∵∠ADC=135°,
∴∠ADC+∠CDE=180°,
∴A、D、E三点共线;
(2)AE=BE+2CM,理由如下:
∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴BE=AD,
∵CD=CE,∠DCE=90°,CM⊥DE,
∴DE=2CM,
∴AE=AD+DE=BE+2CM.
18.(1)①∵线段AM绕点A顺时针旋转与∠BAC相等的角度,
∴,,
∴,
∴,
∴在△NAB和△MAC中,
,
∴△NAB≌△MAC(SAS),
∴;
②证明:∵∠NAM=∠BAC,
∴,
∴∠NAB=∠MAC,
在△NAB和△MAC中,
,
∴△NAB≌△MAC(SAS),
∴NB=CM,
(2)如图:在AC上取一点E,使AE=AB=8,连接PE,过点E作EF⊥BC于F,过A作AD⊥BC于D,
∵∠PAQ=∠CAB,
∴∠CAP=∠BAQ,
在△BAQ和△EAP中,
,
∴△BAQ≌△EAP(SAS),
∴BQ=EP,
要使BQ最小,则有EP最小,而点E是定点,点P是BC上的动点,
∴当EP⊥BC(点P和点F重合)时,EP最小,
即:点P与点F重合,BQ最小,最小值为EF,
∵AB=8,∠ABC=60°,
∴,
∴BD=,AD=,
∵∠BAC=75°,
∴,
∴是等腰直角三角形,
∴,
∴AC,
∴EC,
又∵∠C=45°,
∴是等腰直角三角形,
∴,
∵,
∴,
∴EF=,
故线段BQ长度最小值是.
19.解:(1)连接BD,如图2,
∵线段AP绕点A顺时针旋转90°得到线段AQ,
∴AQ=AP,∠QAP=90°,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠1+∠DAP=∠2+∠DAP=90°。
∴∠1=∠2,
∴△ADQ≌△ABP(SAS),
∴DQ=BP,∠Q=∠3,
∵在Rt△QAP中,∠Q+∠QPA=90°,
∴∠BPD=∠3+∠QPA=90°,
∵在Rt△BPD中,DP2+BP2=BD2,
又∵DQ=BP,BD2=AB2+AD2=2AB2,
∴DP2+DQ2=2AB2;
(2)结论:BP=AB.
理由:如图3中,连接AC,延长CD到N,使得DN=CD,连接AN,QN.
∵AQ=AP,∠QAP=90°,
∴∠AQP=∠APQ=45°,
∵ND=CD,AD⊥NC,
∴AN=AC,
∵四边形ABCD是正方形,
∴∠ANC=∠CAN=45°,
∴∠NAC=90°,
∴∠NAQ+∠QAC=∠QAC+∠PAC=90°,
∴∠NAQ=∠CAP,
又∵AN=AC,AQ=AP,
∴△ANQ≌△ACP(SAS),
同(1)可知△ADQ≌△ABP,
∴DQ=PB,∠AQN=∠APC=45°,
∵∠AQP=45°,
∴∠NQC=90°,
∵CD=DN,
∴D是CN的中点,
∴DQ=CD=DN=AB,
∴PB=AB.
20.(1)证明:如图1,
由旋转得:AH=AG,∠HAG=90°,
∵∠BAC=90°,
∴∠BAH=∠CAG,
∵AB=AC,
∴△ABH≌△ACG(SAS);
(2)①证明:如图2,在等腰直角三角形ABC中,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵点E,F分别为AB,AC的中点,
∴EF是△ABC的中位线,
∴EF∥BC,AE=AB,AF=AC,
∴AE=AF,∠AEF=∠ABC=45°,∠AFE=∠ACB=45°,
∵∠EAH=∠FAG,AH=AG,
∴△AEH≌△AFG(SAS),
∴∠AFG=∠AEH=45°,
∴∠HFG=45°+45°=90°;
②分两种情况:
i)如图3,AQ=QG时,
∵AQ=QG,
∴∠QAG=∠AGQ,
∵AG⊥AH且AG=AH,
∴∠AHG=∠AGH=45°,
∴∠AHG=∠AGH=∠HAQ=∠QAG=45°,
∴∠EAH=∠FAH=45°,
∵AE=AF,AH=AH,
∴△AEH≌△AFH(SAS),
∴∠AHE=∠AHF,
∵∠AHE+∠AHF=180°,
∴∠AHE=∠AHF=90°;
ii)如图4,当AG=QG时,∠GAQ=∠AQG,
∵∠AEH=∠AGQ=45°,
∴∠GAQ=∠AQG==67.5°,
∵∠EAQ=∠HAG=90°,
∴∠EAH=∠GAQ=67.5°,
∴∠AHE=∠AQG=67.5°;
∵H为线段EF上一动点(不与点E,F重合),
∴不存在AG=AQ的情况.
综上,当△AQG为等腰三角形时,∠AHE的度数为67.5°或90°.
21.(1)证明:在正方形ABCD和正方形AEFG中,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∵∠BAE+∠EAD=∠BAD=90°,∠DAG+∠EAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△ADG中,,
∴△ABE≌△ADG(SAS),
∴BE=DG;
(2)①在正方形ABCD和正方形AEFG中,
∴AB=BC,AE=EF,
∵BF=BC,
∴BF=BA,
∴直线BE是AF的垂直平分线;
②∵直线BE是AF的垂直平分线,
∴QF=QA,
∵正方形AEFG中,
∴GF=GA,
∴点G与点Q重合,
正方形AEFG中,AE=3.
∴OA=OE=3,
在Rt△BOA中,,即,
∴OB=3,
由(1)得BE=DG,
∴DG=BE=OB-OE=.
22.解:(1)如图,设AB交CE于点O,
∵点B关于直线AP的对称点为E,
∴AE=AB,∠E=∠ABF,∠AFE=∠AFB,EF=BF,
∵AB=AC,
∴AE=AC,
∴∠E=∠ACE,
∴∠ABF=∠ACE,
∵∠AOC=∠BOF,
∵∠BAC=90°,
∴∠BFO=∠BFE=∠OAC=90°,
∴ ;
(2)①,理由如下:
如图,过点A作AT⊥AF交EC于点T,设AB交CE于点O,
由(1)得:∠BFO=∠OAC=90°,
∴ ,
∴∠AFT=∠AFB-∠BFO=45°,
∵AT⊥AF,
∴∠FAT=90°,
∴∠ATF=45°,
∴∠AFT=∠ATF,
∴AF=AT,
∵ ,
∴ ,
∵∠BAC=∠FAT=90°,
∴∠FAB=∠TAC,
在△FAB和△TAC中,
∵AF=AT,∠FAB=∠TAC,AB=AC,
∴△FAB≌△TAC(SAS),
∴BF=CT,
∵EF=BF,
∴EF=CT,
∴CF-EF=CF-CT=FT= ,
即 ;
②(1)中结论不成立,,理由如下:
如图,过点A作AH⊥AF交EC于点H,设AB交CE于点O,
∵点B关于直线AP的对称点为E,
∴AE=AB,∠E=∠ABF,∠AFE=∠AFB,EF=BF,
∵AB=AC,
∴AE=AC,
∴∠E=∠ACE,
∴∠ABF=∠ACE,
∵∠AOB=∠COF,
∴∠BFC=∠OAB=90°,
∴ ,
∵AH⊥AF,
∴∠FAH=90°,
∴∠AHF=∠AFH=45°,
∴AF=AH,
∵ ,
∴ ,
∵∠BAC=∠FAH=90°,
∴∠FAB=∠HAC,
在△FAB和△HAC中,
∵AF=AH,∠FAB=∠HAC,AB=AC,
∴△FAB≌△HAC(SAS),
∴BF=CH,
∵EF=BF,
∴EF=CH,
∴ ,
即 ;
(3)如图,过点C作CR⊥AE交EA的延长线于点R,
∵∠PAB=∠PAE=30°,
∴∠BAE=60°,
∴∠CAE=∠CAB+∠BAE=90°+60°=150°,
∴∠CAR=180°-150°=30°,
∵CR⊥AR,AC=2,
∴ ,
∴ ,
由(1)知:AE=AC=2,
∴ ,
∴ ,
如图,过点C作CS⊥AE交EA的延长线于点S,
∵∠PAB=∠PAE=30°,∠BAC=90°,
∴∠CAE=90°-30°-30°=30°,
∵AE=AAC=2,
∴ ,
∴ ,
∴ ,
∴ ,
综上所述,EC的长为 或.
23.解:(1)∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∵AB=AC,
∴∠B=∠C,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
故答案为:=;
(2)成立.
证明:由①易知AD=AE,
∴由旋转性质可知∠DAB=∠EAC,
在△DAB和△EAC中,
∴△DAB≌△EAC(SAS),
∴DB=CE;
(3)如图,
将△APB绕点A旋转90°得△AEC,连接PE,
∴△APB≌△AEC,
∴AE=AP=2,EC=BP=1,∠PAE=90°,
∴∠AEP=∠APE=45°,
在Rt△PAE中,由勾股定理可得,PE=2,
在△PEC中,PE2=(2)2=8,CE2=12=1,PC2=32=9,
∵PE2+CE2=PA2,
∴△PEC是直角三角形,
∴∠PEC=90°,
∴∠AEC=135°,
又∵△APB≌△AEC,
∴∠BPA=∠CEA=135°
同课章节目录
