5.1.1任意角 课件(共24张PPT)
文档属性
| 名称 | 5.1.1任意角 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 09:14:26 | ||
图片预览



文档简介
(共24张PPT)
5.1.1任意角
人教A(2019)版
必修一
新知导入
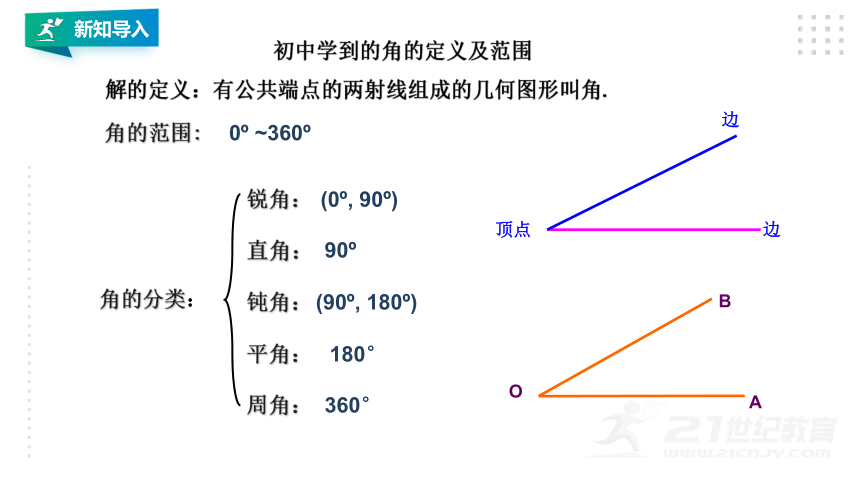
初中学到的角的定义及范围
解的定义:有公共端点的两射线组成的几何图形叫角.
顶点
边
边
A
O
B
角的范围:
0 ~360
角的分类:
锐角:
直角:
钝角:
平角:
周角:
(0 , 90 )
90
(90 , 180 )
180°
360°
新知导入
初中阶段我们学的角在0 ~360 范围的角,但在实际生活中还会遇到其他角的问题,如:
在体操、花样滑冰、跳
台跳水等比赛中,常常听到
“转体720 ”、“向内转体
1080 ”这样的解说。
再如钟表的指针、齿轮、车轮等等转一周3600,
可它转了周又一周怎样从转过的角度来描述它呢?
钟表跑快了10分钟和跑慢10分钟,指针转过的角度
如何描述它呢
可见,在现实生活中,角仅有0 ~360 范围内的角
是不够的,我们必须将角的概念进行推广
新知导入
假如一只钟表快了15分钟,另一只慢了15分钟,指针
转过了同样大小的角度,你将怎样有区别地描述它呢?
顺时针转过900,逆时针旋转90
进一步,假如一只钟表快了2小时15分钟,另一只慢了2
小时15分钟,你又将怎样有区别地描述它呢?
顺时针旋转2周90 ,我们知道一周3600,所以快的这只
顺时针转过了8100。
同理,慢的这只逆时针旋转810
通过上面的例子,我们发现旋转成角可以解决初中角的定
义中不能解决的问题。下面我们从这个角度对角的概念进行推
广和重新认识它。
新知讲解
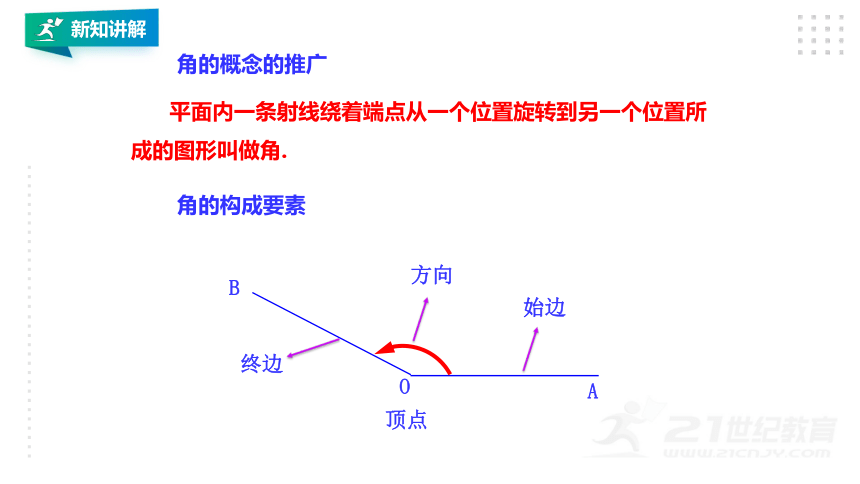
角的概念的推广
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角.
角的构成要素
始边
终边
顶点
A
B
O
方向
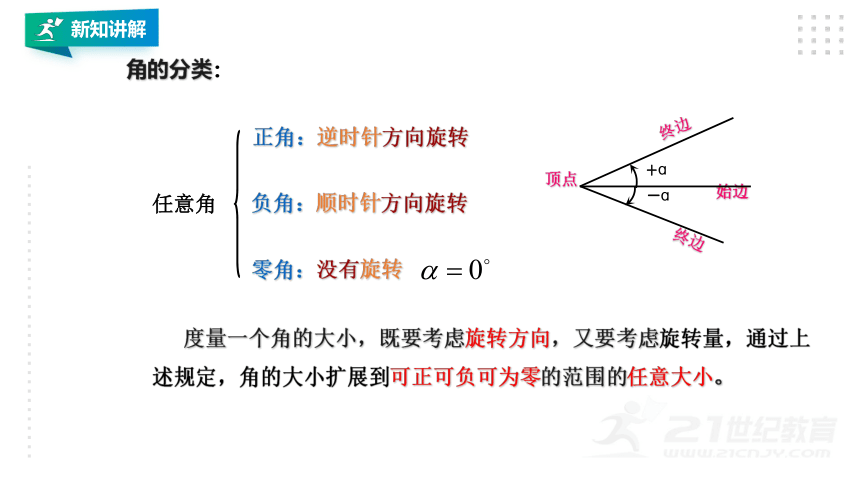
正角:逆时针方向旋转
负角:顺时针方向旋转
零角:没有旋转
度量一个角的大小,既要考虑旋转方向,又要考虑旋转量,通过上述规定,角的大小扩展到可正可负可为零的范围的任意大小。
始边
终边
顶点
+
-
终边
新知讲解
角的分类:
任意角
ɑ
ɑ
角的加减运算
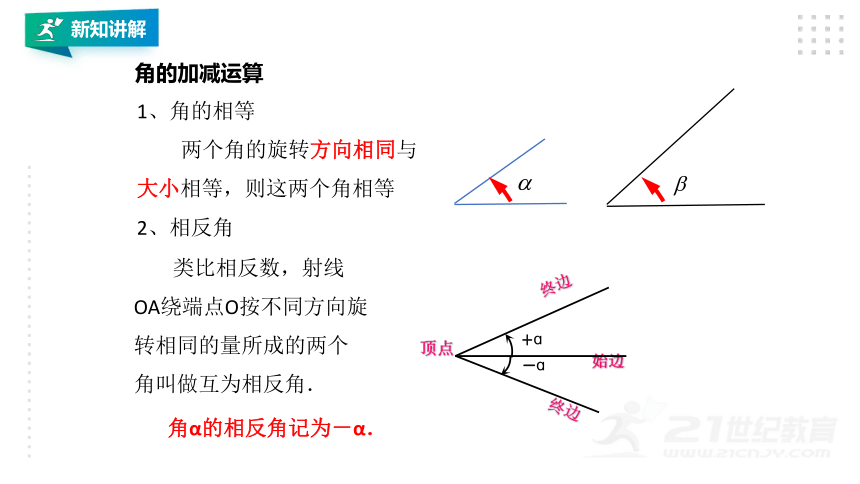
1、角的相等
两个角的旋转方向相同与
大小相等,则这两个角相等
类比相反数,射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相反角.
始边
终边
顶点
+
-
终边
ɑ
ɑ
2、相反角
角α的相反角记为-α.
新知讲解
新知讲解
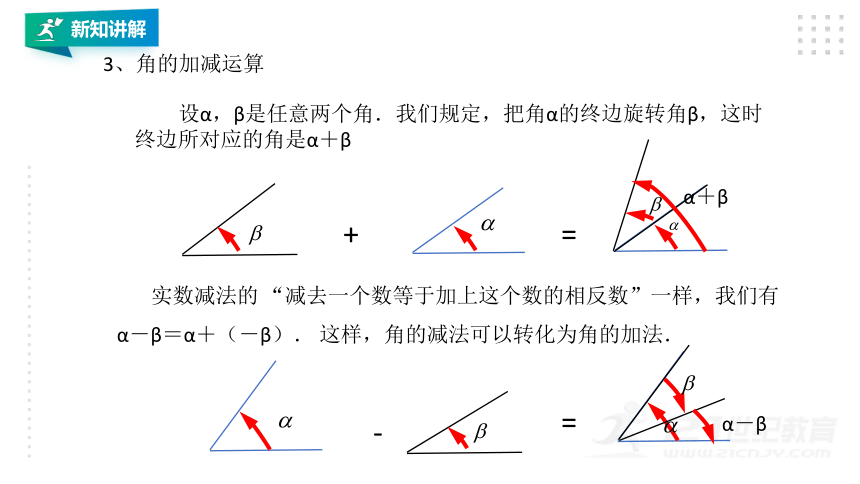
3、角的加减运算
设α,β是任意两个角.我们规定,把角α的终边旋转角β,这时终边所对应的角是α+β
α+β
+
=
实数减法的 “减去一个数等于加上这个数的相反数”一样,我们有
α-β=α+(-β). 这样,角的减法可以转化为角的加法.
-
=
α-β
新知讲解
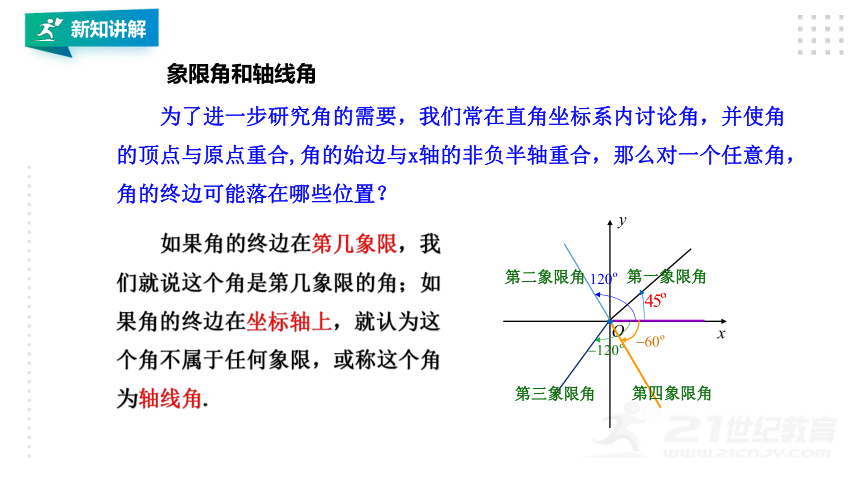
象限角和轴线角
为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角
的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,
角的终边可能落在哪些位置?
第一象限角
第二象限角
第三象限角
第四象限角
如果角的终边在第几象限,我
们就说这个角是第几象限的角;如
果角的终边在坐标轴上,就认为这
个角不属于任何象限,或称这个角
为轴线角.
新知讲解
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
第四象限角
第一象限角
第三象限角
第二象限角
轴线角
下列各角:-50°,405°,210°, -200°,-450°分别是第几象限的角?
新知讲解
第二象限的角一定比第一象限的角大吗?
x
y
o
405°
第一象限角
x
y
o
-200°
第二象限角
象限角只能反映角的终边所在象限,不能反映角的大小.
新知讲解
终边相同的角的集合
-32°,328°,-392°是第几象限的角?这些角有什么内在联系?
-32°
-392°
x
y
o
328°
我们发现,所有与-32°角终边相同的不同角,相差周角的整数倍,连同-32°角在内,可构成一个集合S
我们推广到一般情况:所有与ɑ终边
相同的角的集合S为:
S={β|β=α+k·360°,k∈Z}
合作探究
例1、 在0°~360°范围内,找出与-950012′角终边相同的角,并判
定它是第几象限角.
解:-950012′=129048′-3×360°,所以在0°~360°范围内,
与-950012′角终边相同的角是129048′,它是第二象限角.
例2、写出终边在y轴上的角的集合.
解:在0°~360°范围内,终边在y轴上的角有两个,即90°,
270°角 .
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }
合作探究
合作探究
例3.写出终边在直线y=x上的角的集合S,并把S中适合不等式
-360°≤α<720°的元素β写出来.
解:如图,在直角坐标系中画出直线y=x,可以发现
它与x轴的夹角是45°,在0°~360°范围内,终边在直线y=x上的角有两个:45°,225°.因此,终边在直线y=x上的角的集合
S={β|β=45°+k·360°,k∈Z}
∪ {β|β=225°+k·360°,k∈Z}
={β|β=45°+n·180°,n∈Z}
S中适合不等式-360°≤β<720°的元素β有:
45°-2×180°=-315°,
45°-1×180°=-135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
合作探究
课堂练习
1、分别写出图中终边落在①②两个区域的角α的集合
30°
75°
①
②
解①在0°~360°范围来看,①部分的角α的范
围是30°≤α≤105°,所以在坐标系中角
α的范围是
{α|k·360°+30°≤α≤k·360°+105°,k∈Z}
②在0°~360°范围来看,阴影部分的角α的范围
是210°≤α≤285°,所以在坐标系中角
α的范围是
{α|k·360°+210°≤α≤k·360°+285°,k∈Z}
2、若α是第二象限角,请确定 的终边所在的位置
解法一:①因为α是第二象限角,所以
k·360°+90°<α < k·360°+180°,k∈Z
所以k·180°+45° < < k·180°+90°,k∈Z
k=2n(n∈Z)时,
k·360°+45° < < k·360°+90°,k∈Z
k=2n+1(n∈Z)时,
k·360°+225° < < k·360°+270°,k∈Z
所以 的终边位于第一或者第三象限.
课堂练习
①
②
③
④
②
①
③
④
解法二:运用图示的高阶方法,从
轴正半轴沿逆时针把每个象限
平分成2部分,并且依次标上
①②③④,则标 的就是② 所
在的区域.
课堂练习
课堂总结
任意角
正角:逆时针方向旋转
负角:顺时针方向旋转
零角:没有旋转
象限角:
处于标准位置的角的终边落在第几象限,就把这个角叫做第几象限的角。
终边相同的角的集合:
S={β|β=α+k·360°,k∈Z}
板书设计
任意角的概念
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角.
正角:
负角:
零角:
象限角:
处于标准位置的角的终边落在第几象限,就把这个角叫做第几象限的角。
终边相同的角的集合:
S={β|β=α+k·360°,k∈Z}
作业布置
1、若α是第二象限角,请确定 的终边所在的位置。
3、课本P171练习2、3、4、5
2、写出终边在x轴正半轴、负半轴,y轴正半轴、负半轴上的角
https://www.21cnjy.com/help/help_extract.php
5.1.1任意角
人教A(2019)版
必修一
新知导入
初中学到的角的定义及范围
解的定义:有公共端点的两射线组成的几何图形叫角.
顶点
边
边
A
O
B
角的范围:
0 ~360
角的分类:
锐角:
直角:
钝角:
平角:
周角:
(0 , 90 )
90
(90 , 180 )
180°
360°
新知导入
初中阶段我们学的角在0 ~360 范围的角,但在实际生活中还会遇到其他角的问题,如:
在体操、花样滑冰、跳
台跳水等比赛中,常常听到
“转体720 ”、“向内转体
1080 ”这样的解说。
再如钟表的指针、齿轮、车轮等等转一周3600,
可它转了周又一周怎样从转过的角度来描述它呢?
钟表跑快了10分钟和跑慢10分钟,指针转过的角度
如何描述它呢
可见,在现实生活中,角仅有0 ~360 范围内的角
是不够的,我们必须将角的概念进行推广
新知导入
假如一只钟表快了15分钟,另一只慢了15分钟,指针
转过了同样大小的角度,你将怎样有区别地描述它呢?
顺时针转过900,逆时针旋转90
进一步,假如一只钟表快了2小时15分钟,另一只慢了2
小时15分钟,你又将怎样有区别地描述它呢?
顺时针旋转2周90 ,我们知道一周3600,所以快的这只
顺时针转过了8100。
同理,慢的这只逆时针旋转810
通过上面的例子,我们发现旋转成角可以解决初中角的定
义中不能解决的问题。下面我们从这个角度对角的概念进行推
广和重新认识它。
新知讲解
角的概念的推广
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角.
角的构成要素
始边
终边
顶点
A
B
O
方向
正角:逆时针方向旋转
负角:顺时针方向旋转
零角:没有旋转
度量一个角的大小,既要考虑旋转方向,又要考虑旋转量,通过上述规定,角的大小扩展到可正可负可为零的范围的任意大小。
始边
终边
顶点
+
-
终边
新知讲解
角的分类:
任意角
ɑ
ɑ
角的加减运算
1、角的相等
两个角的旋转方向相同与
大小相等,则这两个角相等
类比相反数,射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相反角.
始边
终边
顶点
+
-
终边
ɑ
ɑ
2、相反角
角α的相反角记为-α.
新知讲解
新知讲解
3、角的加减运算
设α,β是任意两个角.我们规定,把角α的终边旋转角β,这时终边所对应的角是α+β
α+β
+
=
实数减法的 “减去一个数等于加上这个数的相反数”一样,我们有
α-β=α+(-β). 这样,角的减法可以转化为角的加法.
-
=
α-β
新知讲解
象限角和轴线角
为了进一步研究角的需要,我们常在直角坐标系内讨论角,并使角
的顶点与原点重合,角的始边与x轴的非负半轴重合,那么对一个任意角,
角的终边可能落在哪些位置?
第一象限角
第二象限角
第三象限角
第四象限角
如果角的终边在第几象限,我
们就说这个角是第几象限的角;如
果角的终边在坐标轴上,就认为这
个角不属于任何象限,或称这个角
为轴线角.
新知讲解
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
第四象限角
第一象限角
第三象限角
第二象限角
轴线角
下列各角:-50°,405°,210°, -200°,-450°分别是第几象限的角?
新知讲解
第二象限的角一定比第一象限的角大吗?
x
y
o
405°
第一象限角
x
y
o
-200°
第二象限角
象限角只能反映角的终边所在象限,不能反映角的大小.
新知讲解
终边相同的角的集合
-32°,328°,-392°是第几象限的角?这些角有什么内在联系?
-32°
-392°
x
y
o
328°
我们发现,所有与-32°角终边相同的不同角,相差周角的整数倍,连同-32°角在内,可构成一个集合S
我们推广到一般情况:所有与ɑ终边
相同的角的集合S为:
S={β|β=α+k·360°,k∈Z}
合作探究
例1、 在0°~360°范围内,找出与-950012′角终边相同的角,并判
定它是第几象限角.
解:-950012′=129048′-3×360°,所以在0°~360°范围内,
与-950012′角终边相同的角是129048′,它是第二象限角.
例2、写出终边在y轴上的角的集合.
解:在0°~360°范围内,终边在y轴上的角有两个,即90°,
270°角 .
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
而所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }
合作探究
合作探究
例3.写出终边在直线y=x上的角的集合S,并把S中适合不等式
-360°≤α<720°的元素β写出来.
解:如图,在直角坐标系中画出直线y=x,可以发现
它与x轴的夹角是45°,在0°~360°范围内,终边在直线y=x上的角有两个:45°,225°.因此,终边在直线y=x上的角的集合
S={β|β=45°+k·360°,k∈Z}
∪ {β|β=225°+k·360°,k∈Z}
={β|β=45°+n·180°,n∈Z}
S中适合不等式-360°≤β<720°的元素β有:
45°-2×180°=-315°,
45°-1×180°=-135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
合作探究
课堂练习
1、分别写出图中终边落在①②两个区域的角α的集合
30°
75°
①
②
解①在0°~360°范围来看,①部分的角α的范
围是30°≤α≤105°,所以在坐标系中角
α的范围是
{α|k·360°+30°≤α≤k·360°+105°,k∈Z}
②在0°~360°范围来看,阴影部分的角α的范围
是210°≤α≤285°,所以在坐标系中角
α的范围是
{α|k·360°+210°≤α≤k·360°+285°,k∈Z}
2、若α是第二象限角,请确定 的终边所在的位置
解法一:①因为α是第二象限角,所以
k·360°+90°<α < k·360°+180°,k∈Z
所以k·180°+45° < < k·180°+90°,k∈Z
k=2n(n∈Z)时,
k·360°+45° < < k·360°+90°,k∈Z
k=2n+1(n∈Z)时,
k·360°+225° < < k·360°+270°,k∈Z
所以 的终边位于第一或者第三象限.
课堂练习
①
②
③
④
②
①
③
④
解法二:运用图示的高阶方法,从
轴正半轴沿逆时针把每个象限
平分成2部分,并且依次标上
①②③④,则标 的就是② 所
在的区域.
课堂练习
课堂总结
任意角
正角:逆时针方向旋转
负角:顺时针方向旋转
零角:没有旋转
象限角:
处于标准位置的角的终边落在第几象限,就把这个角叫做第几象限的角。
终边相同的角的集合:
S={β|β=α+k·360°,k∈Z}
板书设计
任意角的概念
平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角.
正角:
负角:
零角:
象限角:
处于标准位置的角的终边落在第几象限,就把这个角叫做第几象限的角。
终边相同的角的集合:
S={β|β=α+k·360°,k∈Z}
作业布置
1、若α是第二象限角,请确定 的终边所在的位置。
3、课本P171练习2、3、4、5
2、写出终边在x轴正半轴、负半轴,y轴正半轴、负半轴上的角
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
