2019-2020学年安徽省安庆市外国语学校第一学期九年级12月月考数学试卷(Word版 含解析)
文档属性
| 名称 | 2019-2020学年安徽省安庆市外国语学校第一学期九年级12月月考数学试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 860.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览

文档简介
安庆市外国语学校19-20学年度第一学期九年级十二月月考
数学试卷
一、单选题(本大题共10小题,每小题3分,满分30分)
1.已知sinA=,且∠A为锐角,则∠A=( )
A.30° B.45° C.60° D.75°
2.下列生态环保标志中,是中心对称图形的是( )
3.⊙O的直径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
4.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,求∠B的度数为( )
A.50° B.45° C.60° D.70°
5.在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB的值是( )
A. B. C. D.
6.已知飞机离水平地面的高度为5千米,在飞机上测得该水平地面上某观测目标A的俯角为α,那么这时飞机与目标A的距离为( )
A. B.5sinα C. D.5cosα
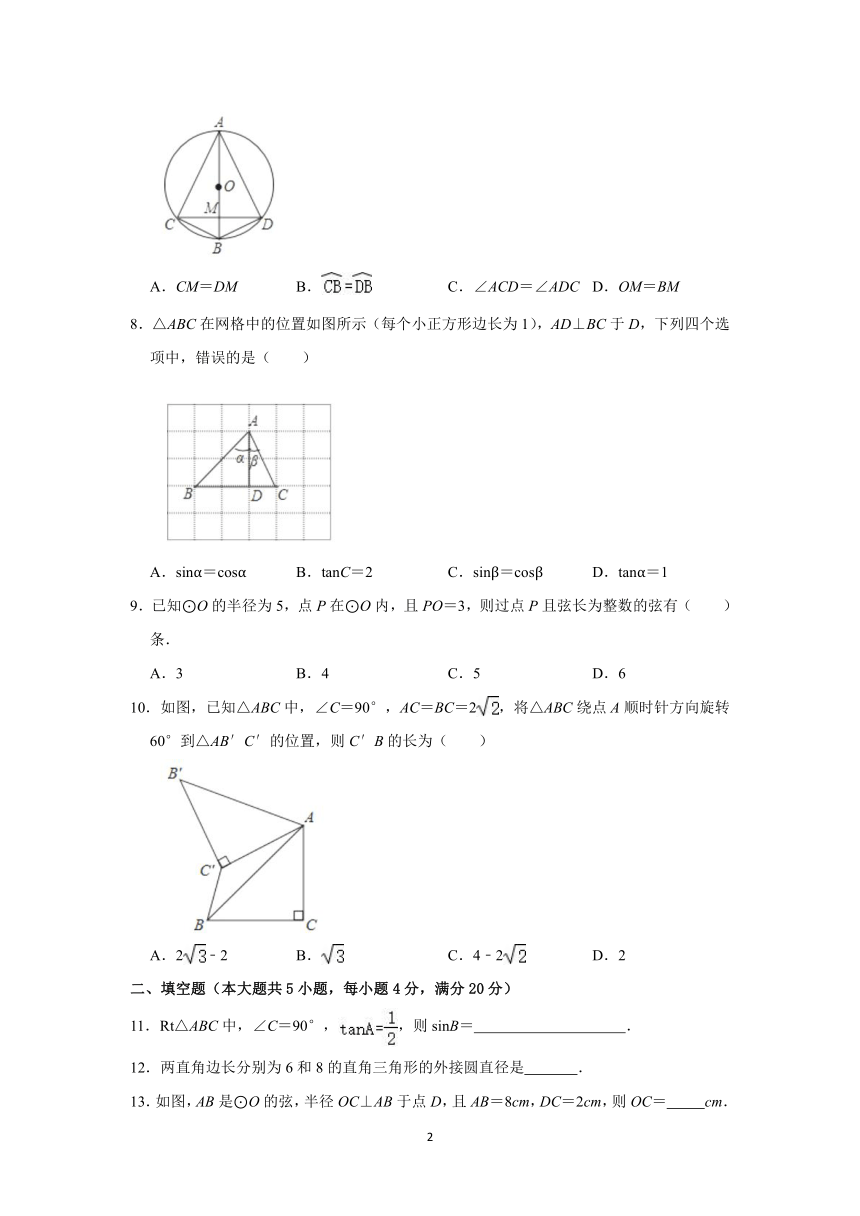
7.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=BM
8.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ=cosβ D.tanα=1
9.已知⊙O的半径为5,点P在⊙O内,且PO=3,则过点P且弦长为整数的弦有( )条.
A.3 B.4 C.5 D.6
10.如图,已知△ABC中,∠C=90°,AC=BC=2,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
A.2﹣2 B. C.4﹣2 D.2
二、填空题(本大题共5小题,每小题4分,满分20分)
11.Rt△ABC中,∠C=90°,,则sinB= .
12.两直角边长分别为6和8的直角三角形的外接圆直径是 .
13.如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= cm.
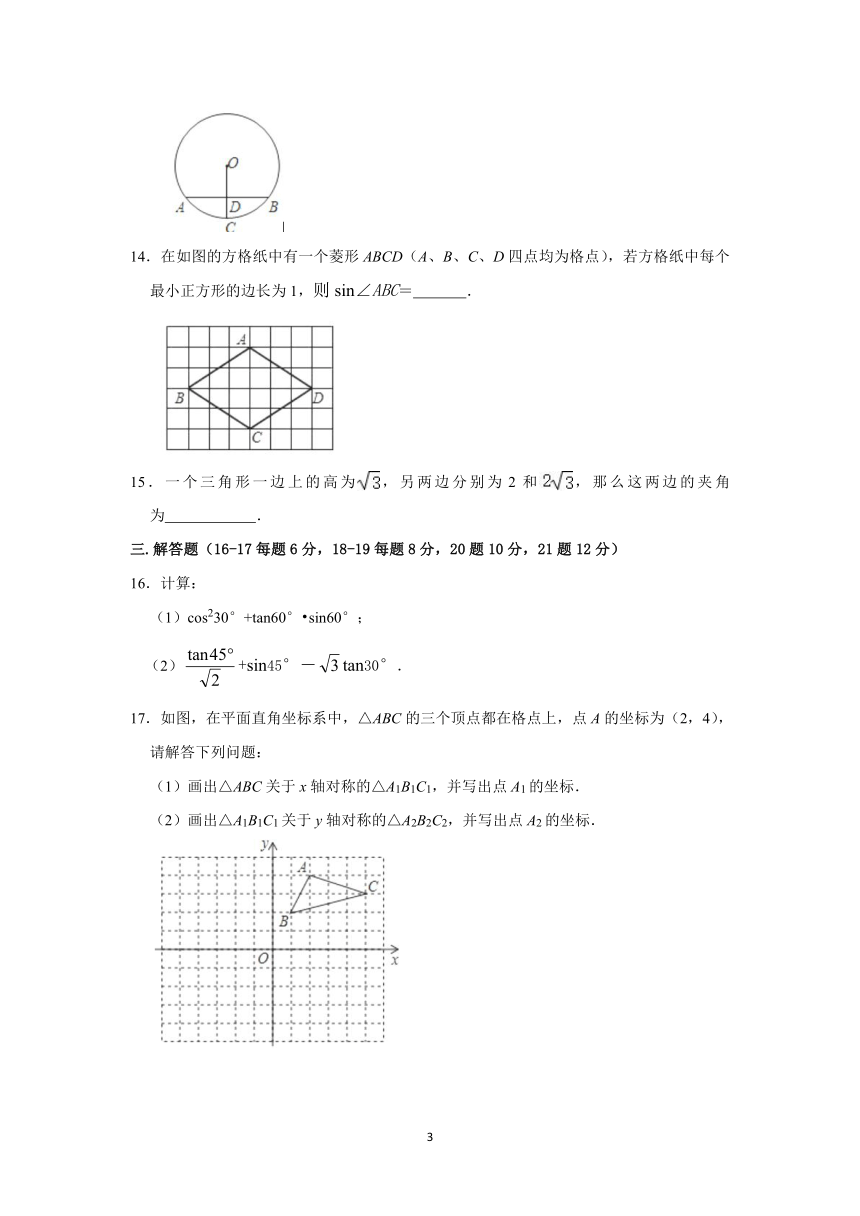
14.在如图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个最小正方形的边长为1,则sin∠ABC= .
15.一个三角形一边上的高为,另两边分别为2和,那么这两边的夹角为 .
三.解答题(16-17每题6分,18-19每题8分,20题10分,21题12分)
16.计算:
(1)cos230°+tan60° sin60°;
(2)+sin45°-tan30°.
17.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点A2的坐标.
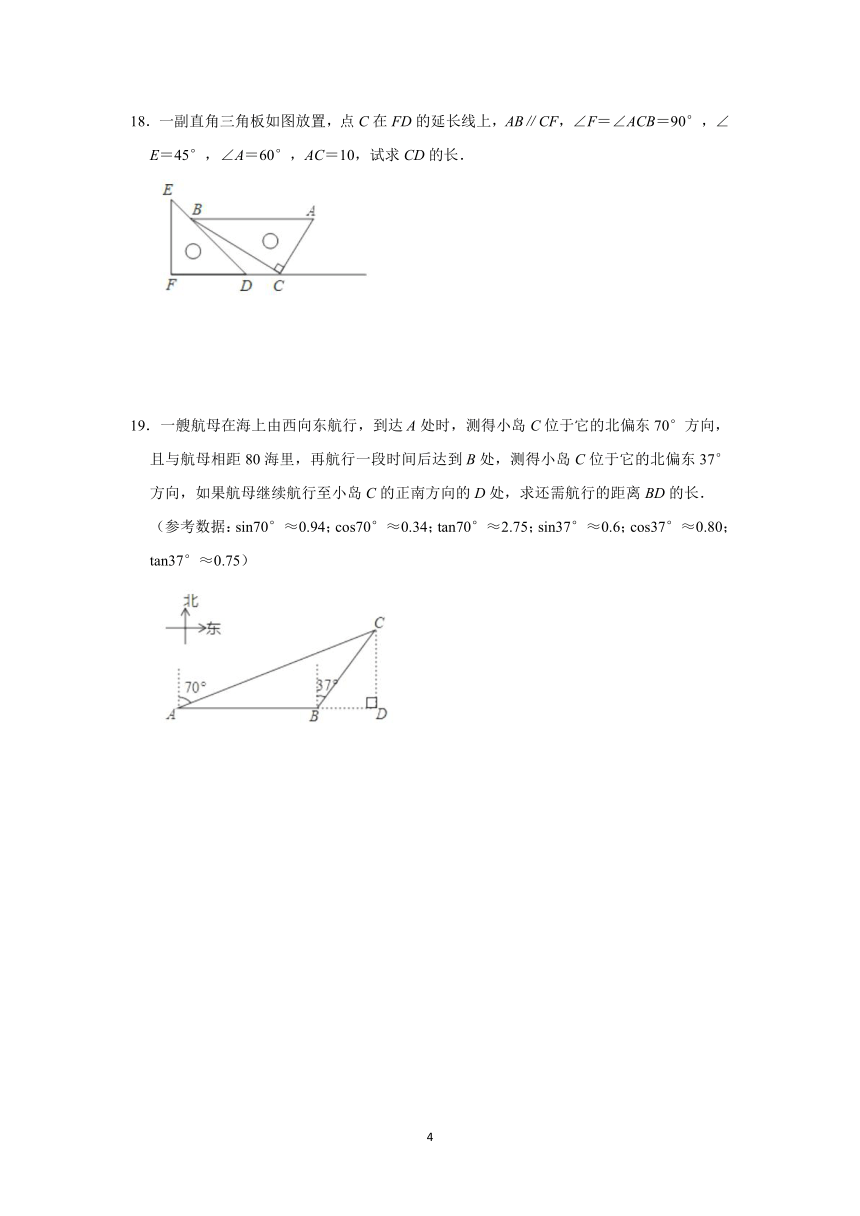
18.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
19.一艘航母在海上由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后达到B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.
(参考数据:sin70°≈0.94;cos70°≈0.34;tan70°≈2.75;sin37°≈0.6;cos37°≈0.80;tan37°≈0.75)
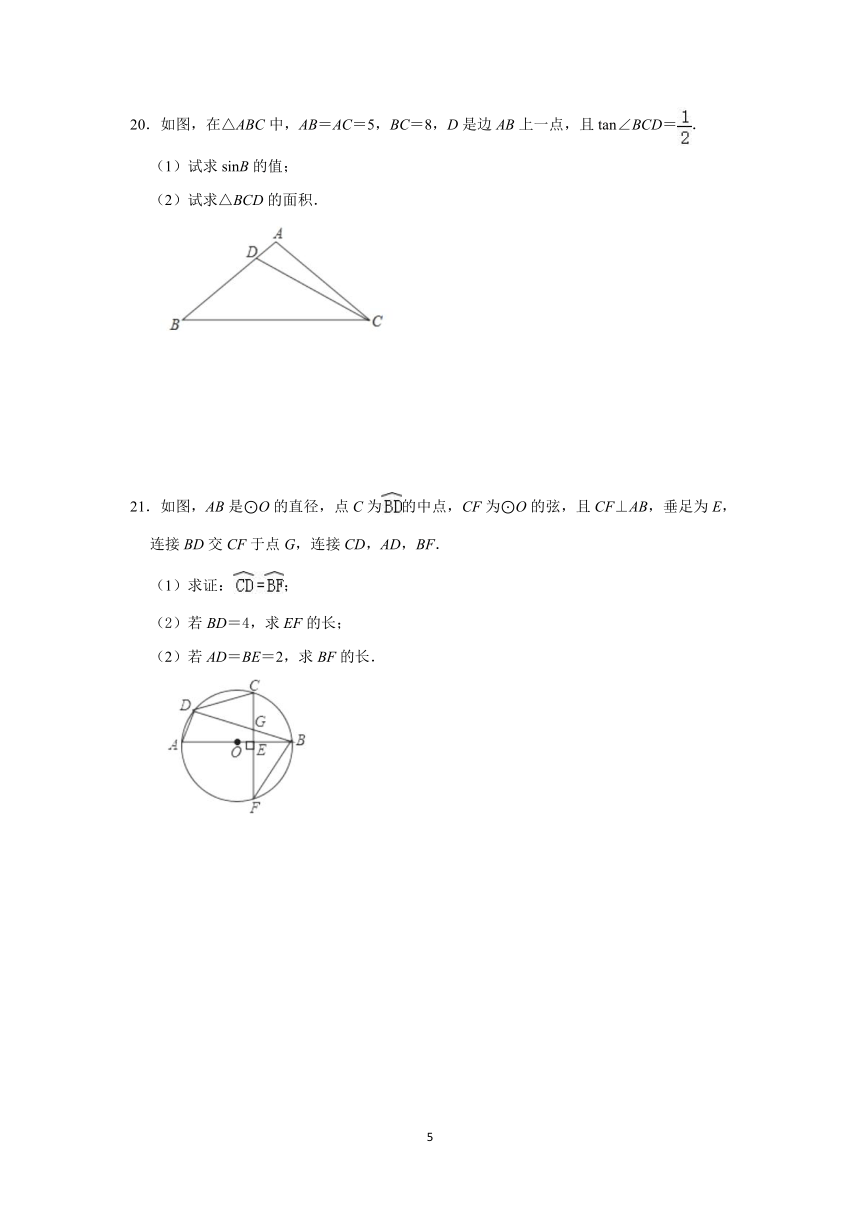
20.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠BCD=.
(1)试求sinB的值;
(2)试求△BCD的面积.
21.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:;
(2)若BD=4,求EF的长;
(2)若AD=BE=2,求BF的长.
安庆市外国语学校19-20学年度第一学期九年级十二月月考数学试卷
参考答案与试题解析
一、单选题(本大题共10小题,每小题3分,满分30分)
1.已知sinA=,且∠A为锐角,则∠A=( )
A.30° B.45° C.60° D.75°
【分析】根据sin30°=求出∠A的值.
【解答】解:∵sinA=,且∠A为锐角,sinA=sin30°=,
∴∠A=30°.
故选:A.
2.下列生态环保标志中,是中心对称图形的是( )
【分析】根据中心对称图形的定义对各选项分析判断即可得解.
【解答】解:A、不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项正确;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误.
故选:B.
3.⊙O的直径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
【分析】根据点与圆的位置关系的判定方法进行判断.
【解答】解:∵⊙O的直径为5cm,
∴⊙O的半径为2.5cm,
∵点A到圆心O的距离为3cm,
即点A到圆心O的距离大于圆的半径,
∴点A在⊙O外.
故选:C.
4.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,求∠B的度数为( )
A.50° B.45° C.60° D.70°
【分析】连OC,由BC=CD=DA,得∠AOD=∠DOC=∠COB,而AB是⊙O的直径,即∠AOC+∠DOC+∠COB=180°,这样就可求出∠BOD的度数.
【解答】解:连OC,如图,
∵BC=CD=DA,
∴∠AOD=∠DOC=∠COB,
又∵AB是⊙O的直径,即∠AOD+∠DOC+∠COB=180°,
∴∠AOD=∠DOC=∠COB=60°,
∴∠B=60°.
故选:C.
5.在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB的值是( )
A. B. C. D.
【分析】先根据勾股定理求出BC的长,再运用三角函数定义解答.
【解答】解:∵Rt△ABC中,∠C=90°,AC=5,AB=13,
∴BC===12.
∴tanB==.
故选:A.
6.已知飞机离水平地面的高度为5千米,在飞机上测得该水平地面上某观测目标A的俯角为α,那么这时飞机与目标A的距离为( )
A. B.5sinα C. D.5cosα
【分析】已知直角三角形的一个锐角和锐角所对的直角边,求斜边,运用三角函数定义解答.
【解答】解:如图:BC为飞机离地面的高度,
所以在Rt△ABC中,∠BAC=α,BC=5,
则AB==,
故选:A.
7.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=BM
【分析】先根据垂径定理得CM=DM,=,=,再根据圆周角定理得到∠ACD=∠ADC,而OM与BM的关系不能判断.
【解答】解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,=,=,
∴∠ACD=∠ADC.
故选:D.
8.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ=cosβ D.tanα=1
【分析】观察图形可知,△ADB是等腰直角三角形,BD=AD=2,AB=2,AD=2,CD=1,AC=,利用锐角三角函数一一计算即可判断.
【解答】解:观察图象可知,△ADB是等腰直角三角形,BD=AD=2,AB=2,AD=2,CD=1,AC=,
∴sinα=cosα=,故A正确,
tanC==2,故B正确,
tanα=1,故D正确,
∵sinβ==,cosβ=,
∴sinβ≠cosβ,故C错误.
故选:C.
9.已知⊙O的半径为5,点P在⊙O内,且PO=3,则过点P且弦长为整数的弦有( )条.
A.3 B.4 C.5 D.6
【分析】过点P最长的弦是10,根据已知条件,可以求出过点P的最短的弦是8,故过点P的弦的长度在8和10之间,所以过点P的弦中长度为整数的弦的条数为4.
【解答】解:如图示,
作弦AB⊥OP于P,
则AP=BP,
在Rt△AOP中,OP=3,OA=5,
AP==4,
∴AB=8,
故过点P的弦的长度在8和10之间,弦为9的有2条,
∴所有过点P的所有弦中取整数的有8,9,10.这三个数,
又∵圆是轴对称图形,
∴过点P的弦中长度为整数的弦的条数为4.
故选:B.
10.如图,已知△ABC中,∠C=90°,AC=BC=2,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
A.2﹣2 B. C.4﹣2 D.2
【分析】如图,作辅助线;证明△ABB′为等边三角形,此为解决问题的关键性结论;证明△BB′C′≌△BAC,得到∠B′BC′=∠ABC′,即可证明BC'是等腰三角形边上的角平分线,即高线,延长BC'交AB'于点D,则BC'=BD﹣C'D.
【解答】解:如图,连接BB′,延长BC'交AB'于点D;由题意得:
AB=AB′,∠BAB′=60°,
∴△ABB′为等边三角形,
∴∠B′BA=60°,BB′=BA;
在△BB′C′与△BAC中,
,
∴△BB′C′≌△BAC(SSS),
∴∠B′BC′=∠ABC′=30°,即BD是等边△ABB′边上的高.
又∵AB′=AB===4,
∴C′D=AB′=2,BD=AB sin60°=4×=2.
∴BC′=BD﹣C′D=2﹣2.
故选:A.
填空题(本大题共5小题,每小题4分,满分20分)
11.Rt△ABC中,∠C=90°,,则sinB= .
【分析】先根据题意设出直角三角形的两直角边,再根据勾股定理求出其斜边,运用三角函数的定义求解.
【解答】解:∵在△ABC中,∠C=90°,tanA=,
设BC=x,则AC=2x,
∴AB==x.
∴sinB==.
12.两直角边长分别为6和8的直角三角形的外接圆直径是 10 .
【分析】根据勾股定理求出三角形的斜边长,根据圆周角定理解答.
【解答】解:由勾股定理得,直角三角形的斜边长==10,
由圆周角定理得,这个直角三角形的外接圆直径为10,
故答案为:10.
13.如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= 5 cm.
【分析】连接OA,根据垂径定理求出AD,根据勾股定理R2=42+(R﹣2)2,计算求出R即可.
【解答】解:连接OA,
∵OC⊥AB,
∴AD=AB=4cm,
设⊙O的半径为R,
由勾股定理得,OA2=AD2+OD2,
∴R2=42+(R﹣2)2,
解得R=5
∴OC=5cm.
故答案为5.
14.在如图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个最小正方形的边长为1,则sin∠ABC= .
【分析】如图,根据菱形的性质,已知AC,BD的长,然后根据菱形的面积公式可求解.
【解答】解:读图可知,AC=4,BD=6,AC=,
则该菱形的面积为4×6×=12,
菱形的面积为 ×× sin∠ABC=6,
sin∠ABC=.
故答案为.
15.一个三角形一边上的高为,另两边分别为2和,那么这两边的夹角为 90°或30° .
【分析】首先画出示意图,①高在三角形内的情况,根据sinB==可求出B的度数,根据sinC==可求出C的度数,从而利用三角形的内角和定理可求出两边的夹角.②高在三角形外的情况,②根据sinB==可求出B的度数,根据sin∠ACD==可求出C的度数,从而利用三角形的外角定理可求出AB和AC的夹角.
【解答】解:①由题意得:AB=2,AC=2,AD=,
∵在RT△ABD中,sinB==,
∴∠B=60°,
∵在RT△ADC中,sinC==,
∴∠C=30°,
∠BAC=180°﹣∠B﹣∠C=180°﹣90°=90°,
即这两边的夹角为90°.
②由题意得:AB=2,AC=2,AD=,
∵在RT△ABD中,sinB==,
∴∠B=30°,
∵在RT△ADC中,sin∠ACD==,
∴∠ACD=60°,
∴∠BAC=∠ACD﹣∠B=60°﹣30°=30°,即两边夹角为30°.
故答案为:90°或30°.
三.解答题(16-17每题6分,18-19每题8分,20题10分,21题12分)
16.计算:
(1)cos230°+tan60° sin60°;
(2)+sin45°-tan30°.
【分析】(1)原式利用特殊角的三角函数值计算即可得到结果;
(2)原式第一项利用负指数幂法则计算,第二项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果.
【解答】解:(1)原式=+×=;
(2)原式=+﹣×=+1.
17.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点A2的坐标.
【分析】(1)作出各点关于x轴的对称点,再顺次连接即可;
(2)作出各点关于y轴的对称点,再顺次连接即可.
【解答】解:(1)如图,△A1B1C1即为所求,A1(2,﹣4)
(2)如图,△A2B2C2即为所求,点A2(﹣2,﹣4).
18.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
【分析】过点B作BM⊥FD于点M,解直角△ACB求出BC,在直角△BMC中求出CM,BM,推出BM=DM,即可求出答案.
【解答】解:
过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=∠ABC=30°.
∴BM=BC sin30°=10×=5,
CM=BC cos30°=10×=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM﹣MD=15﹣5.
19.一艘航母在海上由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后达到B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.
(参考数据:sin70°≈0.94;cos70°≈0.34;tan70°≈2.75;sin37°≈0.6;cos37°≈0.80;tan37°≈0.75)
【分析】根据题意得:∠ACD=70°,∠BCD=37°,AC=80海里,在直角三角形ACD中,由三角函数得出CD=27.2海里,在直角三角形BCD中,得出BD,即可得出答案.
【解答】解:由题意知∠ACD=70°,∠BCD=37°,AC=80海里.
在Rt△ACD中,cos∠ACD=.
∴≈0.34,
∴CD=27.2(海里)
在Rt△BCD中,tan∠BCD=.
∴≈0.75,
∴BD=20.4(海里).
20.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠BCD=.
(1)试求sinB的值;
(2)试求△BCD的面积.
【分析】(1)作AH⊥BC,则△ABH中,根据勾股定理即可求得AH的长,即可求得sinB;
(2)作DE⊥BC,则根据勾股定理可以求得BE的长,求得BC=BE+EC,即4k+6k=8,求得k的值即可求△BCD的面积.
【解答】解:(1)作AH⊥BC,垂足为H,
∵AB=AC=5,∴BH=BC=4,
在△ABH中,AH==3,
∴.
(2)作DE⊥BC,垂足为E,
在△BDE中,sinB=,令DE=3k,
BD=5k,则BE==4k,
又在△CDE中,tan∠BCD=,
则CE==6k,
于是BC=BE+EC,即4k+6k=8,
解得,
∴.
21.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:;
(2)若BD=4,求EF的长;
(2)若AD=BE=2,求BF的长.
【分析】(1)根据垂径分弦定理;
(2)根据垂径分弦定理,等弧对等弦得到EF=BD;
(3)解法一:连接OF,设⊙O的半径为r,由CF=BD列出关于r的勾股方程就能求解;
解法二:如图,作辅助线,构建角平分线和全等三角形,证明Rt△AHC≌Rt△AEC(HL),得AE=AH,再证明Rt△CDH≌Rt△CBE(HL),得DH=BE=2,计算AE和AB的长,证明△BEC∽△BCA,列比例式可得BC的长,就是BF的长.
解法三:连接OC,根据垂径定理和三角形的中位线定理可得OH=1,证明△COE≌△BOH,并利用勾股定理可得结论.
【解答】证明:(1)∵C是的中点,
∴,
∵AB是⊙O的直径,且CF⊥AB,
∴,
∴,
(2)由(1)可知CD=BF,
∵,
∴,
∴BD=CF;
∴EF=CF=BD=2.
(2)解法一:如图,连接OF,设⊙O的半径为r,
Rt△ADB中,BD2=AB2﹣AD2,即BD2=(2r)2﹣22,
Rt△OEF中,OF2=OE2+EF2,即EF2=r2﹣(r﹣2)2,
∵,
∴,
∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2﹣22=4[r2﹣(r﹣2)2],
解得:r=1(舍)或3,
∴BF2=EF2+BE2=32﹣(3﹣2)2+22=12,
∴BF=2;
解法二:如图,过C作CH⊥AD于H,连接AC、BC,
∵,
∴∠HAC=∠BAC,
∵CE⊥AB,
∴CH=CE,
∵AC=AC,
∴Rt△AHC≌Rt△AEC(HL),
∴AE=AH,
∵CH=CE,CD=CB,
∴Rt△CDH≌Rt△CBE(HL),
∴DH=BE=2,
∴AE=AH=2+2=4,
∴AB=4+2=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC=90°,
∵∠EBC=∠ABC,
∴△BEC∽△BCA,
∴,
∴BC2=AB BE=6×2=12,
∴BF=BC=2.
解法三:如图,连接OC,交BD于H,
∵C是的中点,
∴OC⊥BD,
∴DH=BH,
∵OA=OB,
∴OH=AD=1,
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH(AAS),
∴OH=OE=1,
∴CE=EF==2,
∴BF===2.
声明:试题解析著作权
数学试卷
一、单选题(本大题共10小题,每小题3分,满分30分)
1.已知sinA=,且∠A为锐角,则∠A=( )
A.30° B.45° C.60° D.75°
2.下列生态环保标志中,是中心对称图形的是( )
3.⊙O的直径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
4.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,求∠B的度数为( )
A.50° B.45° C.60° D.70°
5.在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB的值是( )
A. B. C. D.
6.已知飞机离水平地面的高度为5千米,在飞机上测得该水平地面上某观测目标A的俯角为α,那么这时飞机与目标A的距离为( )
A. B.5sinα C. D.5cosα
7.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=BM
8.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ=cosβ D.tanα=1
9.已知⊙O的半径为5,点P在⊙O内,且PO=3,则过点P且弦长为整数的弦有( )条.
A.3 B.4 C.5 D.6
10.如图,已知△ABC中,∠C=90°,AC=BC=2,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
A.2﹣2 B. C.4﹣2 D.2
二、填空题(本大题共5小题,每小题4分,满分20分)
11.Rt△ABC中,∠C=90°,,则sinB= .
12.两直角边长分别为6和8的直角三角形的外接圆直径是 .
13.如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= cm.
14.在如图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个最小正方形的边长为1,则sin∠ABC= .
15.一个三角形一边上的高为,另两边分别为2和,那么这两边的夹角为 .
三.解答题(16-17每题6分,18-19每题8分,20题10分,21题12分)
16.计算:
(1)cos230°+tan60° sin60°;
(2)+sin45°-tan30°.
17.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点A2的坐标.
18.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
19.一艘航母在海上由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后达到B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.
(参考数据:sin70°≈0.94;cos70°≈0.34;tan70°≈2.75;sin37°≈0.6;cos37°≈0.80;tan37°≈0.75)
20.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠BCD=.
(1)试求sinB的值;
(2)试求△BCD的面积.
21.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:;
(2)若BD=4,求EF的长;
(2)若AD=BE=2,求BF的长.
安庆市外国语学校19-20学年度第一学期九年级十二月月考数学试卷
参考答案与试题解析
一、单选题(本大题共10小题,每小题3分,满分30分)
1.已知sinA=,且∠A为锐角,则∠A=( )
A.30° B.45° C.60° D.75°
【分析】根据sin30°=求出∠A的值.
【解答】解:∵sinA=,且∠A为锐角,sinA=sin30°=,
∴∠A=30°.
故选:A.
2.下列生态环保标志中,是中心对称图形的是( )
【分析】根据中心对称图形的定义对各选项分析判断即可得解.
【解答】解:A、不是中心对称图形,故本选项错误;
B、是中心对称图形,故本选项正确;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误.
故选:B.
3.⊙O的直径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
A.点A在圆上 B.点A在圆内 C.点A在圆外 D.无法确定
【分析】根据点与圆的位置关系的判定方法进行判断.
【解答】解:∵⊙O的直径为5cm,
∴⊙O的半径为2.5cm,
∵点A到圆心O的距离为3cm,
即点A到圆心O的距离大于圆的半径,
∴点A在⊙O外.
故选:C.
4.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,求∠B的度数为( )
A.50° B.45° C.60° D.70°
【分析】连OC,由BC=CD=DA,得∠AOD=∠DOC=∠COB,而AB是⊙O的直径,即∠AOC+∠DOC+∠COB=180°,这样就可求出∠BOD的度数.
【解答】解:连OC,如图,
∵BC=CD=DA,
∴∠AOD=∠DOC=∠COB,
又∵AB是⊙O的直径,即∠AOD+∠DOC+∠COB=180°,
∴∠AOD=∠DOC=∠COB=60°,
∴∠B=60°.
故选:C.
5.在Rt△ABC中,∠C=90°,AC=5,AB=13,则tanB的值是( )
A. B. C. D.
【分析】先根据勾股定理求出BC的长,再运用三角函数定义解答.
【解答】解:∵Rt△ABC中,∠C=90°,AC=5,AB=13,
∴BC===12.
∴tanB==.
故选:A.
6.已知飞机离水平地面的高度为5千米,在飞机上测得该水平地面上某观测目标A的俯角为α,那么这时飞机与目标A的距离为( )
A. B.5sinα C. D.5cosα
【分析】已知直角三角形的一个锐角和锐角所对的直角边,求斜边,运用三角函数定义解答.
【解答】解:如图:BC为飞机离地面的高度,
所以在Rt△ABC中,∠BAC=α,BC=5,
则AB==,
故选:A.
7.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=BM
【分析】先根据垂径定理得CM=DM,=,=,再根据圆周角定理得到∠ACD=∠ADC,而OM与BM的关系不能判断.
【解答】解:∵AB是⊙O的直径,弦CD⊥AB,
∴CM=DM,=,=,
∴∠ACD=∠ADC.
故选:D.
8.△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列四个选项中,错误的是( )
A.sinα=cosα B.tanC=2 C.sinβ=cosβ D.tanα=1
【分析】观察图形可知,△ADB是等腰直角三角形,BD=AD=2,AB=2,AD=2,CD=1,AC=,利用锐角三角函数一一计算即可判断.
【解答】解:观察图象可知,△ADB是等腰直角三角形,BD=AD=2,AB=2,AD=2,CD=1,AC=,
∴sinα=cosα=,故A正确,
tanC==2,故B正确,
tanα=1,故D正确,
∵sinβ==,cosβ=,
∴sinβ≠cosβ,故C错误.
故选:C.
9.已知⊙O的半径为5,点P在⊙O内,且PO=3,则过点P且弦长为整数的弦有( )条.
A.3 B.4 C.5 D.6
【分析】过点P最长的弦是10,根据已知条件,可以求出过点P的最短的弦是8,故过点P的弦的长度在8和10之间,所以过点P的弦中长度为整数的弦的条数为4.
【解答】解:如图示,
作弦AB⊥OP于P,
则AP=BP,
在Rt△AOP中,OP=3,OA=5,
AP==4,
∴AB=8,
故过点P的弦的长度在8和10之间,弦为9的有2条,
∴所有过点P的所有弦中取整数的有8,9,10.这三个数,
又∵圆是轴对称图形,
∴过点P的弦中长度为整数的弦的条数为4.
故选:B.
10.如图,已知△ABC中,∠C=90°,AC=BC=2,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
A.2﹣2 B. C.4﹣2 D.2
【分析】如图,作辅助线;证明△ABB′为等边三角形,此为解决问题的关键性结论;证明△BB′C′≌△BAC,得到∠B′BC′=∠ABC′,即可证明BC'是等腰三角形边上的角平分线,即高线,延长BC'交AB'于点D,则BC'=BD﹣C'D.
【解答】解:如图,连接BB′,延长BC'交AB'于点D;由题意得:
AB=AB′,∠BAB′=60°,
∴△ABB′为等边三角形,
∴∠B′BA=60°,BB′=BA;
在△BB′C′与△BAC中,
,
∴△BB′C′≌△BAC(SSS),
∴∠B′BC′=∠ABC′=30°,即BD是等边△ABB′边上的高.
又∵AB′=AB===4,
∴C′D=AB′=2,BD=AB sin60°=4×=2.
∴BC′=BD﹣C′D=2﹣2.
故选:A.
填空题(本大题共5小题,每小题4分,满分20分)
11.Rt△ABC中,∠C=90°,,则sinB= .
【分析】先根据题意设出直角三角形的两直角边,再根据勾股定理求出其斜边,运用三角函数的定义求解.
【解答】解:∵在△ABC中,∠C=90°,tanA=,
设BC=x,则AC=2x,
∴AB==x.
∴sinB==.
12.两直角边长分别为6和8的直角三角形的外接圆直径是 10 .
【分析】根据勾股定理求出三角形的斜边长,根据圆周角定理解答.
【解答】解:由勾股定理得,直角三角形的斜边长==10,
由圆周角定理得,这个直角三角形的外接圆直径为10,
故答案为:10.
13.如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8cm,DC=2cm,则OC= 5 cm.
【分析】连接OA,根据垂径定理求出AD,根据勾股定理R2=42+(R﹣2)2,计算求出R即可.
【解答】解:连接OA,
∵OC⊥AB,
∴AD=AB=4cm,
设⊙O的半径为R,
由勾股定理得,OA2=AD2+OD2,
∴R2=42+(R﹣2)2,
解得R=5
∴OC=5cm.
故答案为5.
14.在如图的方格纸中有一个菱形ABCD(A、B、C、D四点均为格点),若方格纸中每个最小正方形的边长为1,则sin∠ABC= .
【分析】如图,根据菱形的性质,已知AC,BD的长,然后根据菱形的面积公式可求解.
【解答】解:读图可知,AC=4,BD=6,AC=,
则该菱形的面积为4×6×=12,
菱形的面积为 ×× sin∠ABC=6,
sin∠ABC=.
故答案为.
15.一个三角形一边上的高为,另两边分别为2和,那么这两边的夹角为 90°或30° .
【分析】首先画出示意图,①高在三角形内的情况,根据sinB==可求出B的度数,根据sinC==可求出C的度数,从而利用三角形的内角和定理可求出两边的夹角.②高在三角形外的情况,②根据sinB==可求出B的度数,根据sin∠ACD==可求出C的度数,从而利用三角形的外角定理可求出AB和AC的夹角.
【解答】解:①由题意得:AB=2,AC=2,AD=,
∵在RT△ABD中,sinB==,
∴∠B=60°,
∵在RT△ADC中,sinC==,
∴∠C=30°,
∠BAC=180°﹣∠B﹣∠C=180°﹣90°=90°,
即这两边的夹角为90°.
②由题意得:AB=2,AC=2,AD=,
∵在RT△ABD中,sinB==,
∴∠B=30°,
∵在RT△ADC中,sin∠ACD==,
∴∠ACD=60°,
∴∠BAC=∠ACD﹣∠B=60°﹣30°=30°,即两边夹角为30°.
故答案为:90°或30°.
三.解答题(16-17每题6分,18-19每题8分,20题10分,21题12分)
16.计算:
(1)cos230°+tan60° sin60°;
(2)+sin45°-tan30°.
【分析】(1)原式利用特殊角的三角函数值计算即可得到结果;
(2)原式第一项利用负指数幂法则计算,第二项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果.
【解答】解:(1)原式=+×=;
(2)原式=+﹣×=+1.
17.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点A2的坐标.
【分析】(1)作出各点关于x轴的对称点,再顺次连接即可;
(2)作出各点关于y轴的对称点,再顺次连接即可.
【解答】解:(1)如图,△A1B1C1即为所求,A1(2,﹣4)
(2)如图,△A2B2C2即为所求,点A2(﹣2,﹣4).
18.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
【分析】过点B作BM⊥FD于点M,解直角△ACB求出BC,在直角△BMC中求出CM,BM,推出BM=DM,即可求出答案.
【解答】解:
过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=∠ABC=30°.
∴BM=BC sin30°=10×=5,
CM=BC cos30°=10×=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5,
∴CD=CM﹣MD=15﹣5.
19.一艘航母在海上由西向东航行,到达A处时,测得小岛C位于它的北偏东70°方向,且与航母相距80海里,再航行一段时间后达到B处,测得小岛C位于它的北偏东37°方向,如果航母继续航行至小岛C的正南方向的D处,求还需航行的距离BD的长.
(参考数据:sin70°≈0.94;cos70°≈0.34;tan70°≈2.75;sin37°≈0.6;cos37°≈0.80;tan37°≈0.75)
【分析】根据题意得:∠ACD=70°,∠BCD=37°,AC=80海里,在直角三角形ACD中,由三角函数得出CD=27.2海里,在直角三角形BCD中,得出BD,即可得出答案.
【解答】解:由题意知∠ACD=70°,∠BCD=37°,AC=80海里.
在Rt△ACD中,cos∠ACD=.
∴≈0.34,
∴CD=27.2(海里)
在Rt△BCD中,tan∠BCD=.
∴≈0.75,
∴BD=20.4(海里).
20.如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠BCD=.
(1)试求sinB的值;
(2)试求△BCD的面积.
【分析】(1)作AH⊥BC,则△ABH中,根据勾股定理即可求得AH的长,即可求得sinB;
(2)作DE⊥BC,则根据勾股定理可以求得BE的长,求得BC=BE+EC,即4k+6k=8,求得k的值即可求△BCD的面积.
【解答】解:(1)作AH⊥BC,垂足为H,
∵AB=AC=5,∴BH=BC=4,
在△ABH中,AH==3,
∴.
(2)作DE⊥BC,垂足为E,
在△BDE中,sinB=,令DE=3k,
BD=5k,则BE==4k,
又在△CDE中,tan∠BCD=,
则CE==6k,
于是BC=BE+EC,即4k+6k=8,
解得,
∴.
21.如图,AB是⊙O的直径,点C为的中点,CF为⊙O的弦,且CF⊥AB,垂足为E,连接BD交CF于点G,连接CD,AD,BF.
(1)求证:;
(2)若BD=4,求EF的长;
(2)若AD=BE=2,求BF的长.
【分析】(1)根据垂径分弦定理;
(2)根据垂径分弦定理,等弧对等弦得到EF=BD;
(3)解法一:连接OF,设⊙O的半径为r,由CF=BD列出关于r的勾股方程就能求解;
解法二:如图,作辅助线,构建角平分线和全等三角形,证明Rt△AHC≌Rt△AEC(HL),得AE=AH,再证明Rt△CDH≌Rt△CBE(HL),得DH=BE=2,计算AE和AB的长,证明△BEC∽△BCA,列比例式可得BC的长,就是BF的长.
解法三:连接OC,根据垂径定理和三角形的中位线定理可得OH=1,证明△COE≌△BOH,并利用勾股定理可得结论.
【解答】证明:(1)∵C是的中点,
∴,
∵AB是⊙O的直径,且CF⊥AB,
∴,
∴,
(2)由(1)可知CD=BF,
∵,
∴,
∴BD=CF;
∴EF=CF=BD=2.
(2)解法一:如图,连接OF,设⊙O的半径为r,
Rt△ADB中,BD2=AB2﹣AD2,即BD2=(2r)2﹣22,
Rt△OEF中,OF2=OE2+EF2,即EF2=r2﹣(r﹣2)2,
∵,
∴,
∴BD=CF,
∴BD2=CF2=(2EF)2=4EF2,
即(2r)2﹣22=4[r2﹣(r﹣2)2],
解得:r=1(舍)或3,
∴BF2=EF2+BE2=32﹣(3﹣2)2+22=12,
∴BF=2;
解法二:如图,过C作CH⊥AD于H,连接AC、BC,
∵,
∴∠HAC=∠BAC,
∵CE⊥AB,
∴CH=CE,
∵AC=AC,
∴Rt△AHC≌Rt△AEC(HL),
∴AE=AH,
∵CH=CE,CD=CB,
∴Rt△CDH≌Rt△CBE(HL),
∴DH=BE=2,
∴AE=AH=2+2=4,
∴AB=4+2=6,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠BEC=90°,
∵∠EBC=∠ABC,
∴△BEC∽△BCA,
∴,
∴BC2=AB BE=6×2=12,
∴BF=BC=2.
解法三:如图,连接OC,交BD于H,
∵C是的中点,
∴OC⊥BD,
∴DH=BH,
∵OA=OB,
∴OH=AD=1,
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH(AAS),
∴OH=OE=1,
∴CE=EF==2,
∴BF===2.
声明:试题解析著作权
同课章节目录
