2019-2020学年安徽省安庆四中第一学期九年级12月月考数学试卷(Word版 含解析)
文档属性
| 名称 | 2019-2020学年安徽省安庆四中第一学期九年级12月月考数学试卷(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 944.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览


文档简介
安庆四中2019-2020学年第一学期九年级12月月考数学试卷
一.选择题(本题共10小题,每题3分,满分30分)
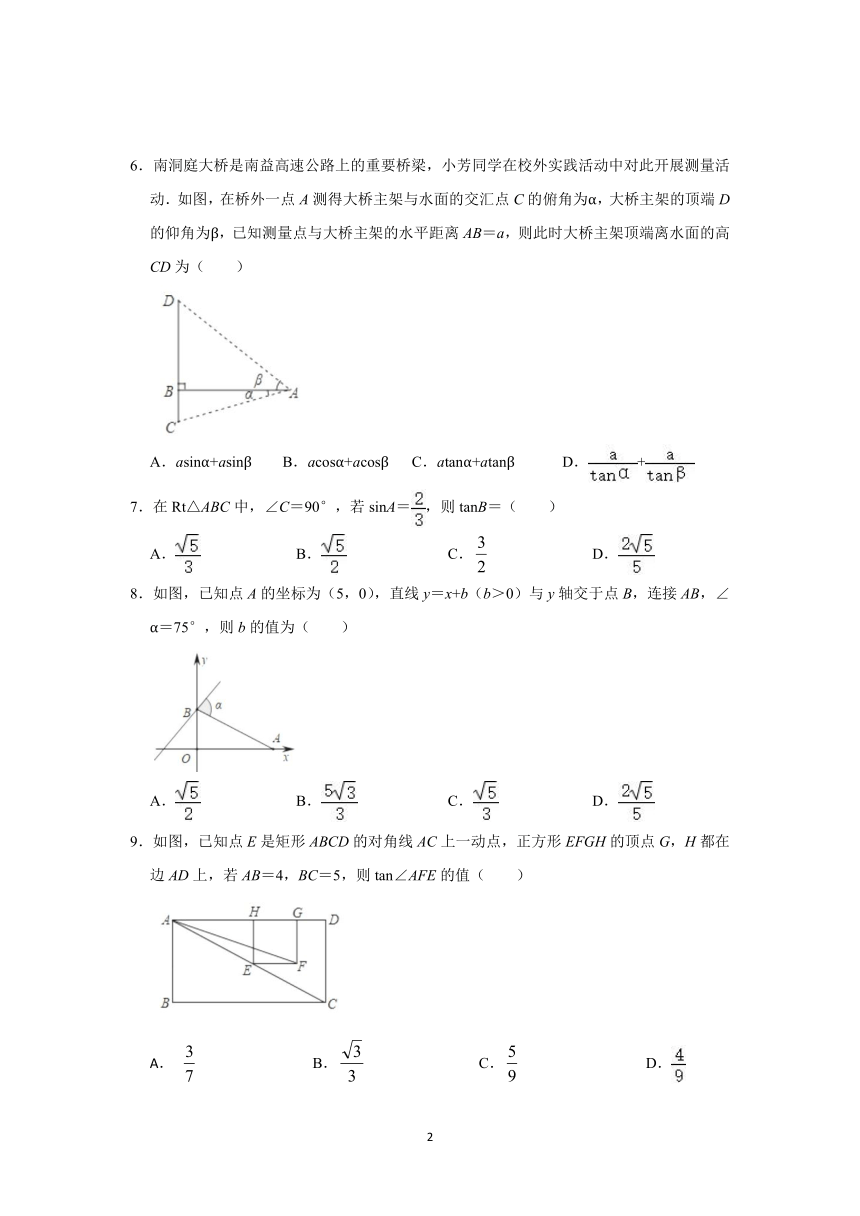
1.下列说法中正确的是( )
A.两个等腰三角形相似
B.有一个内角是30°的两个直角三角形相似
C.两个直角三角形相似
D.有一个锐角是30°的两个等腰三角形相似
2.下列条件中能判断△ABC∽△A′B′C′的是( )
A.∠A=∠B,∠A′=∠B
B.∠A=∠A′,∠B=∠C
C.∠A=∠A′,
D.∠A=∠A′,AB=AC,A′B′=A′C′
3.如图,已知△ADE∽△ABC,若AD:AB=1:3,△ABC的面积为9,则△ADE的面积为( )
A.1 B.3 C.27 D.81
4.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正弦值为( )
A.2 B. C. D.
5.一座拦河大坝的横截面是梯形ABCD,AD∥BC,∠B=90°,AD=6米,坡面CD的坡度i=1:,且BC=CD,那么拦河大坝的高是( )米.
A.18 B.24 C.20 D.12
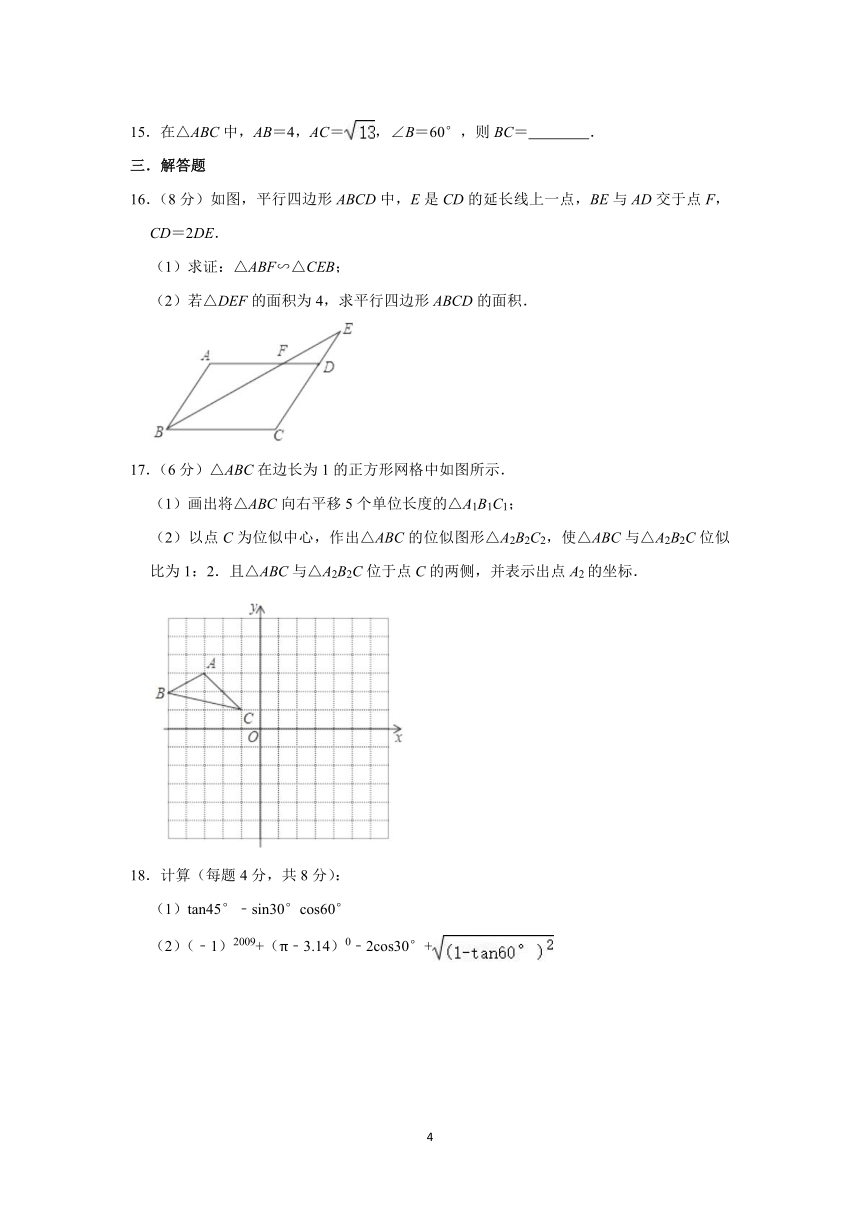
6.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ C.atanα+atanβ D.+
7.在Rt△ABC中,∠C=90°,若sinA=,则tanB=( )
A. B. C. D.
8.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A. B. C. D.
9.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G,H都在边AD上,若AB=4,BC=5,则tan∠AFE的值( )
B. C. D.
10.如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A. B. C. D.
二.填空题(本题共4小题,每题5分,满分20分)
11.若a:b:c=2:4:5且3a﹣b+2c=6,则﹣2a+b+3c= .
12.如图,矩形ABCD的顶点C,D分别在反比例函数y=(x>0).y=(x>0)的图象上,顶点A,B在x轴上,连接OC,交DA于点E,则= .
13.如图,面积为64的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=2,则小正方形的周长为 .
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
15.在△ABC中,AB=4,AC=,∠B=60°,则BC= .
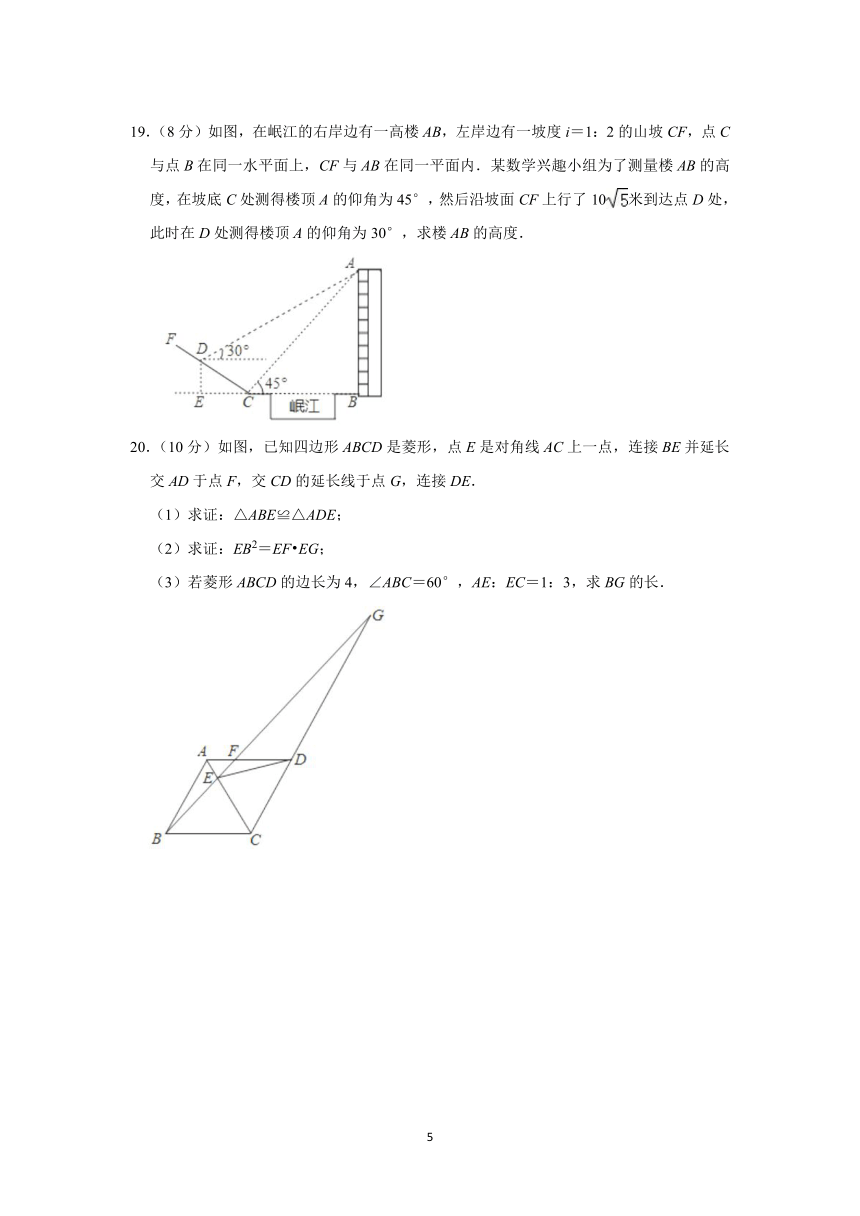
三.解答题
16.(8分)如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为4,求平行四边形ABCD的面积.
17.(6分)△ABC在边长为1的正方形网格中如图所示.
(1)画出将△ABC向右平移5个单位长度的△A1B1C1;
(2)以点C为位似中心,作出△ABC的位似图形△A2B2C2,使△ABC与△A2B2C位似比为1:2.且△ABC与△A2B2C位于点C的两侧,并表示出点A2的坐标.
18.计算(每题4分,共8分):
(1)tan45°﹣sin30°cos60°
(2)(﹣1)2009+(π﹣3.14)0﹣2cos30°+
19.(8分)如图,在岷江的右岸边有一高楼AB,左岸边有一坡度i=1:2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行了10米到达点D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.
20.(10分)如图,已知四边形ABCD是菱形,点E是对角线AC上一点,连接BE并延长交AD于点F,交CD的延长线于点G,连接DE.
(1)求证:△ABE≌△ADE;
(2)求证:EB2=EF EG;
(3)若菱形ABCD的边长为4,∠ABC=60°,AE:EC=1:3,求BG的长.
21.(10分)已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
安庆四中2020-2021学年第一学期九年级12月月考数学试卷
参考答案与试题解析
一.选择题(本题共10小题,每题3分,满分30分)
1.下列说法中正确的是( )
A.两个等腰三角形相似
B.有一个内角是30°的两个直角三角形相似
C.两个直角三角形相似
D.有一个锐角是30°的两个等腰三角形相似
【分析】根据相似三角形的判定方法对各个选项进行分析,从而得到答案.
【解答】解:A、不正确,因为没有说明角或边相等的条件,故不一定相似;
B、正确,因为其三对角均对应相等,符合相似三角形的判定条件,故一定相似.
C、不正确,只知道一个直角相等,不符合相似三角形判定的条件,故不一定相似;
D、不正确,因为30°的角可以为底角也可以为顶角,故两三角形不一定相似;
故选:B.
2.下列条件中能判断△ABC∽△A′B′C′的是( )
A.∠A=∠B,∠A′=∠B
B.∠A=∠A′,∠B=∠C
C.∠A=∠A′,
D.∠A=∠A′,AB=AC,A′B′=A′C′
【分析】根据相似三角形的判定方法,对各选项分析判断后利用排除法求解.
【解答】解:A、从∠A=∠B,∠A′=∠B′找不出两组对应相等的角,所以不能判断△ABC∽△A′B′C′,故本选项错误;
B、∵∠A=∠A′,∠B=∠C,
只能找到一组对应角∠A=∠A′,所以不能判断△ABC∽△A′B′C′,故本选项错误;
C、相等的角∠A=∠A′,不是边AB、BC,A′B′、B′C′的夹角,所以不能判断△ABC∽△A′B′C′,故本选项错误;
D、AB=AC,∠A=∠A′,A′B′=A′C′,可以利用两边对应成比例,夹角相等两三角形相似判断△ABC∽△A′B′C′,故本选项正确.
故选:D.
3.如图,已知△ADE∽△ABC,若AD:AB=1:3,△ABC的面积为9,则△ADE的面积为( )
A.1 B.3 C.27 D.81
【分析】根据相似三角形的性质得出=()2,代入求出即可.
【解答】解:∵△ADE∽△ABC,AD:AB=1:3,
∴=()2,
∵△ABC的面积为9,
∴=,
∴S△ADE=1,
故选:A.
4.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正弦值为( )
A.2 B. C. D.
【分析】延长CB交网格于D,连接AD,则∠ADC=45°+45°=90°,由勾股定理得出AD==,AC==,由三角函数定义即可得出答案.
【解答】解:延长CB交网格于D,连接AD,如图所示:
则∠ADC=45°+45°=90°,
∵AD==,AC==,
∴∠ACB的正弦值===;
故选:C.
5.一座拦河大坝的横截面是梯形ABCD,AD∥BC,∠B=90°,AD=6米,坡面CD的坡度i=1:,且BC=CD,那么拦河大坝的高是( )米.
A.18 B.24 C.20 D.12
【分析】作DE⊥BC于E点,得到BE=AD=5,设BC=CD=x,表示出CE=(x﹣5)米,利用CD的坡度i=1:,得到DE=(x﹣5)米,利用在直角三角形DEC中,DE2+EC2=DC2得到(x﹣5)2+[(x﹣5)]2=x2,求得x即可.
【解答】解:作DE⊥BC于E点,
∵∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=6,
设BC=CD=x
则CE=(x﹣6)米,
∵CD的坡度i=1:,
∴DE:EC=1:,
∴DE=(x﹣6)米,
∵在直角三角形DEC中,DE2+EC2=DC2,
∴(x﹣6)2+[(x﹣6)]2=x2,
解得:x=30.
∴CE=24,
∴DE=18.
故答案为18.
故选:A.
6.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ
C.atanα+atanβ D.+
【分析】在Rt△ABD和Rt△ABC中,由三角函数得出BC=atanα,BD=atanβ,得出CD=BC+BD=atanα+atanβ即可.
【解答】解:在Rt△ABD和Rt△ABC中,AB=a,tanα=,tanβ=,
∴BC=atanα,BD=atanβ,
∴CD=BC+BD=atanα+atanβ;
故选:C.
7.7.在Rt△ABC中,∠C=90°,若sinA=,则tanB=( )
A. B. C. D.
【分析】根据互为余角三角函数关系,可得cosB,根据同角三角函数的关系,可得答案.
【解答】解:由在Rt△ABC中,∠C=90°,若sinA=,得cosB=sinA=.
由同角三角函数,得
sinB==,
tanB==,
故选:B.
8.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A. B. C. D.
【分析】根据一次函数的解析式,得到直线与y轴的夹角,结合∠α=75°,求出∠OBA的度数,根据点A的坐标为(5,0),得到OA=5,利用三角函数,计算出OB的值,得到点B的坐标,代入y=x+b,即可得到答案.
【解答】解:根据题意得:直线y=x+b与y轴的夹角为45°,
∠OBA=180°﹣45°﹣∠α
=180°﹣45°﹣75°
=60°,
∵OA=5,
∴OB==,
即点B的坐标为:(0,),
把点B(0,)代入y=x+b得:
b=,
故选:B.
9.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G,H都在边AD上,若AB=4,BC=5,则tan∠AFE的值( )
B. C. D.
【分析】由△AEH∽△ACD,找到EH和AH关系,从而得到FG和AG关系,根据tan∠AFE=tan∠FAG求解.
【解答】解:∵EH∥CD,
∴△AEH∽△ACD.
∴=.
设EH=4x,则AH=5x,
∴HG=GF=4x.
∴tan∠AFE=tan∠FAG==.
故选:D.
10.如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A. B. C. D.
【分析】作PH⊥AD于H,根据四边形ABEF是菱形,∠ABC=60°,AB=4,得到AB=AF=4,∠ABF=∠ADB=30°,AP⊥BF,从而得到PH=,DH=5,然后利用锐角三角函数的定义求解即可.
【解答】解:作PH⊥AD于H,
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
∵∠ABC=60°,AB=4,
∴AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=AB=2,
∴PH=,DH=5,
∴tan∠ADP==.
故选:A.
二.填空题(共5小题)
11.若a:b:c=2:4:5且3a﹣b+2c=6,则﹣2a+b+3c= .
【分析】直接利用已知表示出各数,进而得出a,b,c的值,进而求出答案.
【解答】解:∵a:b:c=2:4:5,
∴设a=2x,则b=4x,c=5x,
∵3a﹣b+2c=6,
∴6x﹣4x+10x=6,
解得:x=,
故a=1,b=2,c=,
∴﹣2a+b+3c=﹣2×1+2+3×=.
故答案为:.
12.如图,矩形ABCD的顶点C,D分别在反比例函数y=(x>0).y=(x>0)的图象上,顶点A,B在x轴上,连接OC,交DA于点E,则= .
【分析】根据反比例函数图象上点的坐标特征以及反比例函数k的几何意义,求出矩形CBOH的面积为8,矩形ADHO的面积为3,进一步求得OA:CD=3:5,通过证得△AOE∽△DCE,得出==.
【解答】解:延长CD交y轴于点H,
∵点C在反比例函数y=(x>0)的图象上,
∴矩形CBOH的面积为8,
∵点D分别在反比例函数y=(x>0)的图象上,
∴矩形ADHO的面积为3,
∴矩形ABCD的面积为:8﹣3=5,
∴OA:CD=3:5,
∵CD∥OA,
∴△AOE∽△DCE,
∴==,
故答案为:.
13.如图,面积为36的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=2,则小正方形的周长长为 .
【分析】先根据正方形ABCD的面积为644,求得大正方形的边长;利用“一线三等角”证得∠BEF=∠CFD,进而得△BEF∽∠CFD,利用相似三角形的性质求得BE;再利用勾股定理求得正方形EFGH的边长即可.
【解答】解:∵正方形ABCD的面积为64
∴BC=CD=8
∵BF=2
∴CF=6
∵在正方形ABCD和EFGH中
∠B=∠C=∠EFG=90°
∴∠BEF+∠BFE=90°,∠CFD+∠BFE=90°
∴∠BEF=∠CFD
∴△BEF∽△CFD
∴=
∴=
∴BE=
∴在Rt△BEF中,由勾股定理得:
EF==
∴小正方形的周长为10.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
【分析】先由AF平分∠CAB,CD⊥AB,过点E作EG垂直于AC,利用角平分线的性质定理得EG等于DE,易得Rt△AED全等于Rt△AEG以及∠DCA等于∠B,从而求得AD,AG,CG,然后在Rt△CEG中,由勾股定理求出EG,即为DE的长度.
【解答】解:过点E作EG⊥AC于点G,
又∵AF平分∠CAB,CD⊥AB,
∴EG=ED,
在Rt△AED和Rt△AEG中,
∴Rt△AED≌Rt△AEG(HL),
AG=AD.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠BAC=∠DCA+∠BAC=90°,
∴∠DCA=∠B,
∵AC=6,sinB=,
∴sin∠DCA=sinB=,
∴=,
∴AD=,
∴DC===,
∴AG=AD=,CG=AC﹣AG=,
∴在Rt△CEG中,CE2=EG2+CG2,
∴(DC﹣ED)2=(DC﹣EG)2=EG2+CG2
∴,
∴EG=,
∴DE=.
故答案为:.
解法二:如图,过点E作EG⊥AC于G.设EC=x.
则EG=DE=x,
∴CD=x+x=,
∴x=3,
∴DE=.
15.在△ABC中,AB=4,AC=,∠B=60°,则BC= 3或1 .
【分析】根据已知得出两种不同的图形,分别作出三角形的高,利用勾股定理求出即可.
【解答】解:如图1所示:作AD⊥BC,
∵AB=4,AC=,∠B=60°,
∴∠BAD=30°,
∴BD=AB=2,
∴AD==2,
∴DC===1,
∴BC=2+1=3,
如图2所示:作AD⊥BC延长线于点D,
∵AB=4,AC=,∠B=60°,
∴∠BAD=30°,
∴BD=AB=2,
∴AD==2,
∴DC===1,
∴BC=2﹣1=1.
故答案为:3或1.
三.解答题(共6小题)
16.如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为4,求平行四边形ABCD的面积.
【分析】(1)由四边形ABCD是平行四边形,得AD∥BC,进而推断出△ABF∽△CEB.
(2)由四边形ABCD是平行四边形,得AB∥CD,即AB∥CE,AB=CD,故△ABF∽△DEF.根据相似三角形的性质,由△DEF的面积为2,故可求平行四边形ABCD的面积.
【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EFD=∠EBC,∠EDF=∠C.
∴△EDF∽△ECB.
(2)由(1)得:△EDF∽△ECB.
∵CD=2DE,
∴.
∴.
∴.
∴S四边形DCBF=8S△EDF=32.
∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥CE,AB=CD.
∴∠ABF=∠E,∠A=∠EDF.
∴△ABF∽△DEF.
又∵CD=2DE,
∴AB=2DE.
∴S△ABF=4S△DEF=16.
∴S平形四边形ABCD==S△ABF+S四边形BCDF=32+16=48.
17.△ABC在边长为1的正方形网格中如图所示.
(1)画出将△ABC向右平移5个单位长度的△A1B1C1;
(2)以点C为位似中心,作出△ABC的位似图形△A2B2C2,使△ABC与△A2B2C位似比为1:2.且△ABC与△A2B2C位于点C的两侧,并表示出点A2的坐标.
【分析】(1)利用点平移的坐标规律写出A1、B1、C1的坐标,然后描点即可;
(2)利用网格特点,延长AC到A2使CA2=2CA,延长BC到B2,使CB2=2CB,从而得到△A2B2C,然后写出点A2的坐标.
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C为所作;点A2的坐标为(3,﹣3).
18.计算:
(1)tan45°﹣sin30°cos60°
(2)(﹣1)2009+(π﹣3.14)0﹣2cos30°+
【分析】(1)直接利用特殊角的三角函数值分别代入得出答案;
(2)直接利用二次根式以及零指数幂的性质分别化简得出答案.
【解答】解:(1)原式=1﹣×
=;
(2)原式=﹣1+1﹣2×+﹣1
=﹣1+1﹣+﹣1
=﹣1.
19.如图,在岷江的右岸边有一高楼AB,左岸边有一坡度i=1:2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行了10米到达点D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.
【分析】由i==,DE2+EC2=CD2,解得DE=10m,EC=20m,过点D作DG⊥AB于G,过点C作CH⊥DG于H,则四边形DEBG、四边形DECH、四边形BCHG都是矩形,证得AB=BC,设AB=BC=xm,则AG=(x﹣10)m,DG=(x+20)m,在Rt△ADG中,=tan∠ADG,代入即可得出结果.
【解答】解:在Rt△DEC中,∵i==,DE2+EC2=CD2,CD=10,
∴DE2+(2DE)2=(10)2,
解得:DE=10(m),
∴EC=20m,
过点D作DG⊥AB于G,过点C作CH⊥DG于H,如图所示:
则四边形DEBG、四边形DECH、四边形BCHG都是矩形,
∵∠ACB=45°,AB⊥BC,
∴AB=BC,
设AB=BC=xm,则AG=(x﹣10)m,DG=(x+20)m,
在Rt△ADG中,∵=tan∠ADG,
∴=,
解得:x=25+15,
经检验,x=25+15是方程的解.
答:楼AB的高度为(25+15)米.
20.如图,已知四边形ABCD是菱形,点E是对角线AC上一点,连接BE并延长交AD于点F,交CD的延长线于点G,连接DE.
(1)求证:△ABE≌△ADE;
(2)求证:EB2=EF EG;
(3)若菱形ABCD的边长为4,∠ABC=60°,AE:EC=1:3,求BG的长.
【分析】(1)用SAS证明即可;
(2)先证明△EDF∽△EGD,得到ED2=EF EG,代换ED=EB即可;
(3)根据已知先求出BE和EF值,再根据EB2=EF EG求出EG值,最后用BG=BE+EG计算即可.
【解答】解:(1)∵四边形ABCD是菱形,
∴AB=AD,∠BAC=∠DAC,
又AE=AE,
∴△ABE≌△ADE(SAS);
(2)∵AB∥CG,
∴∠ABG=∠EGD,
由(1)得△ABE≌△ADE,
∴ED=EB,∠ABG=∠ADE,
∴∠EGD=∠ADE,
∵∠FED=∠DEG,
∴△EDF∽△EGD,
∴,
所以ED2=EF EG;
∴EB2=EF EG;
(3)∵AB=BC,∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB=4.
连接BD交AC于O,则AC⊥BD,OA=OC=2,OB=2,
∵AE:EC=1:3,
∴AE=OE=1.
∴BE=.
∵AD∥BC,
∴,
∴EF=BE=.
由(2)得EB2=EF EG,
∴EG=,
∴BG=BE+EG=4.
21.已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
【分析】(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
(3)本题分两种情况讨论:若点E在线段BC上,y=,x的范围为x>0;若点E在边BC的延长线上,y=,x的范围为x>1.
【解答】解:(1)∵AB∥DF,
∴=,
∵BE=2CE,AB=3,
∴=,
∴CF=;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3﹣x.
又∵CF=1.5,
∴AM=MF=﹣x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(﹣x)2,
∴x=,(1分)
∴DM=,AM=,
∴sin∠DAB1==;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.
同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴=,
∴DF=FC=,
设DN=x,则AN=NF=x+.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+)2,
∴x=.(1分)
∴DN=,AN=sin∠DAB1==;
(3)若点E在线段BC上,y=,x的范围为x>0;
若点E在边BC的延长线上,y=,x的范围为x>1.
一.选择题(本题共10小题,每题3分,满分30分)
1.下列说法中正确的是( )
A.两个等腰三角形相似
B.有一个内角是30°的两个直角三角形相似
C.两个直角三角形相似
D.有一个锐角是30°的两个等腰三角形相似
2.下列条件中能判断△ABC∽△A′B′C′的是( )
A.∠A=∠B,∠A′=∠B
B.∠A=∠A′,∠B=∠C
C.∠A=∠A′,
D.∠A=∠A′,AB=AC,A′B′=A′C′
3.如图,已知△ADE∽△ABC,若AD:AB=1:3,△ABC的面积为9,则△ADE的面积为( )
A.1 B.3 C.27 D.81
4.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正弦值为( )
A.2 B. C. D.
5.一座拦河大坝的横截面是梯形ABCD,AD∥BC,∠B=90°,AD=6米,坡面CD的坡度i=1:,且BC=CD,那么拦河大坝的高是( )米.
A.18 B.24 C.20 D.12
6.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ C.atanα+atanβ D.+
7.在Rt△ABC中,∠C=90°,若sinA=,则tanB=( )
A. B. C. D.
8.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A. B. C. D.
9.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G,H都在边AD上,若AB=4,BC=5,则tan∠AFE的值( )
B. C. D.
10.如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A. B. C. D.
二.填空题(本题共4小题,每题5分,满分20分)
11.若a:b:c=2:4:5且3a﹣b+2c=6,则﹣2a+b+3c= .
12.如图,矩形ABCD的顶点C,D分别在反比例函数y=(x>0).y=(x>0)的图象上,顶点A,B在x轴上,连接OC,交DA于点E,则= .
13.如图,面积为64的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=2,则小正方形的周长为 .
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
15.在△ABC中,AB=4,AC=,∠B=60°,则BC= .
三.解答题
16.(8分)如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为4,求平行四边形ABCD的面积.
17.(6分)△ABC在边长为1的正方形网格中如图所示.
(1)画出将△ABC向右平移5个单位长度的△A1B1C1;
(2)以点C为位似中心,作出△ABC的位似图形△A2B2C2,使△ABC与△A2B2C位似比为1:2.且△ABC与△A2B2C位于点C的两侧,并表示出点A2的坐标.
18.计算(每题4分,共8分):
(1)tan45°﹣sin30°cos60°
(2)(﹣1)2009+(π﹣3.14)0﹣2cos30°+
19.(8分)如图,在岷江的右岸边有一高楼AB,左岸边有一坡度i=1:2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行了10米到达点D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.
20.(10分)如图,已知四边形ABCD是菱形,点E是对角线AC上一点,连接BE并延长交AD于点F,交CD的延长线于点G,连接DE.
(1)求证:△ABE≌△ADE;
(2)求证:EB2=EF EG;
(3)若菱形ABCD的边长为4,∠ABC=60°,AE:EC=1:3,求BG的长.
21.(10分)已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
安庆四中2020-2021学年第一学期九年级12月月考数学试卷
参考答案与试题解析
一.选择题(本题共10小题,每题3分,满分30分)
1.下列说法中正确的是( )
A.两个等腰三角形相似
B.有一个内角是30°的两个直角三角形相似
C.两个直角三角形相似
D.有一个锐角是30°的两个等腰三角形相似
【分析】根据相似三角形的判定方法对各个选项进行分析,从而得到答案.
【解答】解:A、不正确,因为没有说明角或边相等的条件,故不一定相似;
B、正确,因为其三对角均对应相等,符合相似三角形的判定条件,故一定相似.
C、不正确,只知道一个直角相等,不符合相似三角形判定的条件,故不一定相似;
D、不正确,因为30°的角可以为底角也可以为顶角,故两三角形不一定相似;
故选:B.
2.下列条件中能判断△ABC∽△A′B′C′的是( )
A.∠A=∠B,∠A′=∠B
B.∠A=∠A′,∠B=∠C
C.∠A=∠A′,
D.∠A=∠A′,AB=AC,A′B′=A′C′
【分析】根据相似三角形的判定方法,对各选项分析判断后利用排除法求解.
【解答】解:A、从∠A=∠B,∠A′=∠B′找不出两组对应相等的角,所以不能判断△ABC∽△A′B′C′,故本选项错误;
B、∵∠A=∠A′,∠B=∠C,
只能找到一组对应角∠A=∠A′,所以不能判断△ABC∽△A′B′C′,故本选项错误;
C、相等的角∠A=∠A′,不是边AB、BC,A′B′、B′C′的夹角,所以不能判断△ABC∽△A′B′C′,故本选项错误;
D、AB=AC,∠A=∠A′,A′B′=A′C′,可以利用两边对应成比例,夹角相等两三角形相似判断△ABC∽△A′B′C′,故本选项正确.
故选:D.
3.如图,已知△ADE∽△ABC,若AD:AB=1:3,△ABC的面积为9,则△ADE的面积为( )
A.1 B.3 C.27 D.81
【分析】根据相似三角形的性质得出=()2,代入求出即可.
【解答】解:∵△ADE∽△ABC,AD:AB=1:3,
∴=()2,
∵△ABC的面积为9,
∴=,
∴S△ADE=1,
故选:A.
4.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正弦值为( )
A.2 B. C. D.
【分析】延长CB交网格于D,连接AD,则∠ADC=45°+45°=90°,由勾股定理得出AD==,AC==,由三角函数定义即可得出答案.
【解答】解:延长CB交网格于D,连接AD,如图所示:
则∠ADC=45°+45°=90°,
∵AD==,AC==,
∴∠ACB的正弦值===;
故选:C.
5.一座拦河大坝的横截面是梯形ABCD,AD∥BC,∠B=90°,AD=6米,坡面CD的坡度i=1:,且BC=CD,那么拦河大坝的高是( )米.
A.18 B.24 C.20 D.12
【分析】作DE⊥BC于E点,得到BE=AD=5,设BC=CD=x,表示出CE=(x﹣5)米,利用CD的坡度i=1:,得到DE=(x﹣5)米,利用在直角三角形DEC中,DE2+EC2=DC2得到(x﹣5)2+[(x﹣5)]2=x2,求得x即可.
【解答】解:作DE⊥BC于E点,
∵∠B=90°,
∴四边形ABED是矩形,
∴BE=AD=6,
设BC=CD=x
则CE=(x﹣6)米,
∵CD的坡度i=1:,
∴DE:EC=1:,
∴DE=(x﹣6)米,
∵在直角三角形DEC中,DE2+EC2=DC2,
∴(x﹣6)2+[(x﹣6)]2=x2,
解得:x=30.
∴CE=24,
∴DE=18.
故答案为18.
故选:A.
6.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A测得大桥主架与水面的交汇点C的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高CD为( )
A.asinα+asinβ B.acosα+acosβ
C.atanα+atanβ D.+
【分析】在Rt△ABD和Rt△ABC中,由三角函数得出BC=atanα,BD=atanβ,得出CD=BC+BD=atanα+atanβ即可.
【解答】解:在Rt△ABD和Rt△ABC中,AB=a,tanα=,tanβ=,
∴BC=atanα,BD=atanβ,
∴CD=BC+BD=atanα+atanβ;
故选:C.
7.7.在Rt△ABC中,∠C=90°,若sinA=,则tanB=( )
A. B. C. D.
【分析】根据互为余角三角函数关系,可得cosB,根据同角三角函数的关系,可得答案.
【解答】解:由在Rt△ABC中,∠C=90°,若sinA=,得cosB=sinA=.
由同角三角函数,得
sinB==,
tanB==,
故选:B.
8.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A. B. C. D.
【分析】根据一次函数的解析式,得到直线与y轴的夹角,结合∠α=75°,求出∠OBA的度数,根据点A的坐标为(5,0),得到OA=5,利用三角函数,计算出OB的值,得到点B的坐标,代入y=x+b,即可得到答案.
【解答】解:根据题意得:直线y=x+b与y轴的夹角为45°,
∠OBA=180°﹣45°﹣∠α
=180°﹣45°﹣75°
=60°,
∵OA=5,
∴OB==,
即点B的坐标为:(0,),
把点B(0,)代入y=x+b得:
b=,
故选:B.
9.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G,H都在边AD上,若AB=4,BC=5,则tan∠AFE的值( )
B. C. D.
【分析】由△AEH∽△ACD,找到EH和AH关系,从而得到FG和AG关系,根据tan∠AFE=tan∠FAG求解.
【解答】解:∵EH∥CD,
∴△AEH∽△ACD.
∴=.
设EH=4x,则AH=5x,
∴HG=GF=4x.
∴tan∠AFE=tan∠FAG==.
故选:D.
10.如图,平行四边形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD与∠ABC的平分线AE、BF交于点P,连接PD,则tan∠ADP的值为( )
A. B. C. D.
【分析】作PH⊥AD于H,根据四边形ABEF是菱形,∠ABC=60°,AB=4,得到AB=AF=4,∠ABF=∠ADB=30°,AP⊥BF,从而得到PH=,DH=5,然后利用锐角三角函数的定义求解即可.
【解答】解:作PH⊥AD于H,
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAE=∠AEB.
∵AE是角平分线,
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=BE,
∴四边形ABEF是菱形.
∵∠ABC=60°,AB=4,
∴AB=AF=4,∠ABF=∠AFB=30°,AP⊥BF,
∴AP=AB=2,
∴PH=,DH=5,
∴tan∠ADP==.
故选:A.
二.填空题(共5小题)
11.若a:b:c=2:4:5且3a﹣b+2c=6,则﹣2a+b+3c= .
【分析】直接利用已知表示出各数,进而得出a,b,c的值,进而求出答案.
【解答】解:∵a:b:c=2:4:5,
∴设a=2x,则b=4x,c=5x,
∵3a﹣b+2c=6,
∴6x﹣4x+10x=6,
解得:x=,
故a=1,b=2,c=,
∴﹣2a+b+3c=﹣2×1+2+3×=.
故答案为:.
12.如图,矩形ABCD的顶点C,D分别在反比例函数y=(x>0).y=(x>0)的图象上,顶点A,B在x轴上,连接OC,交DA于点E,则= .
【分析】根据反比例函数图象上点的坐标特征以及反比例函数k的几何意义,求出矩形CBOH的面积为8,矩形ADHO的面积为3,进一步求得OA:CD=3:5,通过证得△AOE∽△DCE,得出==.
【解答】解:延长CD交y轴于点H,
∵点C在反比例函数y=(x>0)的图象上,
∴矩形CBOH的面积为8,
∵点D分别在反比例函数y=(x>0)的图象上,
∴矩形ADHO的面积为3,
∴矩形ABCD的面积为:8﹣3=5,
∴OA:CD=3:5,
∵CD∥OA,
∴△AOE∽△DCE,
∴==,
故答案为:.
13.如图,面积为36的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=2,则小正方形的周长长为 .
【分析】先根据正方形ABCD的面积为644,求得大正方形的边长;利用“一线三等角”证得∠BEF=∠CFD,进而得△BEF∽∠CFD,利用相似三角形的性质求得BE;再利用勾股定理求得正方形EFGH的边长即可.
【解答】解:∵正方形ABCD的面积为64
∴BC=CD=8
∵BF=2
∴CF=6
∵在正方形ABCD和EFGH中
∠B=∠C=∠EFG=90°
∴∠BEF+∠BFE=90°,∠CFD+∠BFE=90°
∴∠BEF=∠CFD
∴△BEF∽△CFD
∴=
∴=
∴BE=
∴在Rt△BEF中,由勾股定理得:
EF==
∴小正方形的周长为10.
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CB于点F.交CD于点E.若AC=6,sinB=,则DE的长为 .
【分析】先由AF平分∠CAB,CD⊥AB,过点E作EG垂直于AC,利用角平分线的性质定理得EG等于DE,易得Rt△AED全等于Rt△AEG以及∠DCA等于∠B,从而求得AD,AG,CG,然后在Rt△CEG中,由勾股定理求出EG,即为DE的长度.
【解答】解:过点E作EG⊥AC于点G,
又∵AF平分∠CAB,CD⊥AB,
∴EG=ED,
在Rt△AED和Rt△AEG中,
∴Rt△AED≌Rt△AEG(HL),
AG=AD.
∵∠ACB=90°,CD⊥AB,
∴∠B+∠BAC=∠DCA+∠BAC=90°,
∴∠DCA=∠B,
∵AC=6,sinB=,
∴sin∠DCA=sinB=,
∴=,
∴AD=,
∴DC===,
∴AG=AD=,CG=AC﹣AG=,
∴在Rt△CEG中,CE2=EG2+CG2,
∴(DC﹣ED)2=(DC﹣EG)2=EG2+CG2
∴,
∴EG=,
∴DE=.
故答案为:.
解法二:如图,过点E作EG⊥AC于G.设EC=x.
则EG=DE=x,
∴CD=x+x=,
∴x=3,
∴DE=.
15.在△ABC中,AB=4,AC=,∠B=60°,则BC= 3或1 .
【分析】根据已知得出两种不同的图形,分别作出三角形的高,利用勾股定理求出即可.
【解答】解:如图1所示:作AD⊥BC,
∵AB=4,AC=,∠B=60°,
∴∠BAD=30°,
∴BD=AB=2,
∴AD==2,
∴DC===1,
∴BC=2+1=3,
如图2所示:作AD⊥BC延长线于点D,
∵AB=4,AC=,∠B=60°,
∴∠BAD=30°,
∴BD=AB=2,
∴AD==2,
∴DC===1,
∴BC=2﹣1=1.
故答案为:3或1.
三.解答题(共6小题)
16.如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为4,求平行四边形ABCD的面积.
【分析】(1)由四边形ABCD是平行四边形,得AD∥BC,进而推断出△ABF∽△CEB.
(2)由四边形ABCD是平行四边形,得AB∥CD,即AB∥CE,AB=CD,故△ABF∽△DEF.根据相似三角形的性质,由△DEF的面积为2,故可求平行四边形ABCD的面积.
【解答】解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠EFD=∠EBC,∠EDF=∠C.
∴△EDF∽△ECB.
(2)由(1)得:△EDF∽△ECB.
∵CD=2DE,
∴.
∴.
∴.
∴S四边形DCBF=8S△EDF=32.
∵四边形ABCD是平行四边形,
∴AB∥CD,即AB∥CE,AB=CD.
∴∠ABF=∠E,∠A=∠EDF.
∴△ABF∽△DEF.
又∵CD=2DE,
∴AB=2DE.
∴S△ABF=4S△DEF=16.
∴S平形四边形ABCD==S△ABF+S四边形BCDF=32+16=48.
17.△ABC在边长为1的正方形网格中如图所示.
(1)画出将△ABC向右平移5个单位长度的△A1B1C1;
(2)以点C为位似中心,作出△ABC的位似图形△A2B2C2,使△ABC与△A2B2C位似比为1:2.且△ABC与△A2B2C位于点C的两侧,并表示出点A2的坐标.
【分析】(1)利用点平移的坐标规律写出A1、B1、C1的坐标,然后描点即可;
(2)利用网格特点,延长AC到A2使CA2=2CA,延长BC到B2,使CB2=2CB,从而得到△A2B2C,然后写出点A2的坐标.
【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C为所作;点A2的坐标为(3,﹣3).
18.计算:
(1)tan45°﹣sin30°cos60°
(2)(﹣1)2009+(π﹣3.14)0﹣2cos30°+
【分析】(1)直接利用特殊角的三角函数值分别代入得出答案;
(2)直接利用二次根式以及零指数幂的性质分别化简得出答案.
【解答】解:(1)原式=1﹣×
=;
(2)原式=﹣1+1﹣2×+﹣1
=﹣1+1﹣+﹣1
=﹣1.
19.如图,在岷江的右岸边有一高楼AB,左岸边有一坡度i=1:2的山坡CF,点C与点B在同一水平面上,CF与AB在同一平面内.某数学兴趣小组为了测量楼AB的高度,在坡底C处测得楼顶A的仰角为45°,然后沿坡面CF上行了10米到达点D处,此时在D处测得楼顶A的仰角为30°,求楼AB的高度.
【分析】由i==,DE2+EC2=CD2,解得DE=10m,EC=20m,过点D作DG⊥AB于G,过点C作CH⊥DG于H,则四边形DEBG、四边形DECH、四边形BCHG都是矩形,证得AB=BC,设AB=BC=xm,则AG=(x﹣10)m,DG=(x+20)m,在Rt△ADG中,=tan∠ADG,代入即可得出结果.
【解答】解:在Rt△DEC中,∵i==,DE2+EC2=CD2,CD=10,
∴DE2+(2DE)2=(10)2,
解得:DE=10(m),
∴EC=20m,
过点D作DG⊥AB于G,过点C作CH⊥DG于H,如图所示:
则四边形DEBG、四边形DECH、四边形BCHG都是矩形,
∵∠ACB=45°,AB⊥BC,
∴AB=BC,
设AB=BC=xm,则AG=(x﹣10)m,DG=(x+20)m,
在Rt△ADG中,∵=tan∠ADG,
∴=,
解得:x=25+15,
经检验,x=25+15是方程的解.
答:楼AB的高度为(25+15)米.
20.如图,已知四边形ABCD是菱形,点E是对角线AC上一点,连接BE并延长交AD于点F,交CD的延长线于点G,连接DE.
(1)求证:△ABE≌△ADE;
(2)求证:EB2=EF EG;
(3)若菱形ABCD的边长为4,∠ABC=60°,AE:EC=1:3,求BG的长.
【分析】(1)用SAS证明即可;
(2)先证明△EDF∽△EGD,得到ED2=EF EG,代换ED=EB即可;
(3)根据已知先求出BE和EF值,再根据EB2=EF EG求出EG值,最后用BG=BE+EG计算即可.
【解答】解:(1)∵四边形ABCD是菱形,
∴AB=AD,∠BAC=∠DAC,
又AE=AE,
∴△ABE≌△ADE(SAS);
(2)∵AB∥CG,
∴∠ABG=∠EGD,
由(1)得△ABE≌△ADE,
∴ED=EB,∠ABG=∠ADE,
∴∠EGD=∠ADE,
∵∠FED=∠DEG,
∴△EDF∽△EGD,
∴,
所以ED2=EF EG;
∴EB2=EF EG;
(3)∵AB=BC,∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB=4.
连接BD交AC于O,则AC⊥BD,OA=OC=2,OB=2,
∵AE:EC=1:3,
∴AE=OE=1.
∴BE=.
∵AD∥BC,
∴,
∴EF=BE=.
由(2)得EB2=EF EG,
∴EG=,
∴BG=BE+EG=4.
21.已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.
(1)如图1,若点E在线段BC上,求CF的长;
(2)求sin∠DAB1的值;
(3)如果题设中“BE=2CE”改为“=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).
【分析】(1)利用平行线性质以及线段比求出CF的值;
(2)本题要分两种方法讨论:①若点E在线段BC上;②若点E在边BC的延长线上.需运用勾股定理求出与之相联的线段;
(3)本题分两种情况讨论:若点E在线段BC上,y=,x的范围为x>0;若点E在边BC的延长线上,y=,x的范围为x>1.
【解答】解:(1)∵AB∥DF,
∴=,
∵BE=2CE,AB=3,
∴=,
∴CF=;
(2)①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.
由题意翻折得:∠1=∠2.
∵AB∥DF,
∴∠1=∠F,
∴∠2=∠F,
∴AM=MF.
设DM=x,则CM=3﹣x.
又∵CF=1.5,
∴AM=MF=﹣x,
在Rt△ADM中,AD2+DM2=AM2,
∴32+x2=(﹣x)2,
∴x=,(1分)
∴DM=,AM=,
∴sin∠DAB1==;
②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.
同理可得:AN=NF.
∵BE=2CE,
∴BC=CE=AD.
∵AD∥BE,
∴=,
∴DF=FC=,
设DN=x,则AN=NF=x+.
在Rt△ADN中,AD2+DN2=AN2,
∴32+x2=(x+)2,
∴x=.(1分)
∴DN=,AN=sin∠DAB1==;
(3)若点E在线段BC上,y=,x的范围为x>0;
若点E在边BC的延长线上,y=,x的范围为x>1.
同课章节目录
