对数函数的图象和性质(获奖)
图片预览










文档简介
(共36张PPT)
给我空间、时间和对数,我可以创造宇宙。
——伽利略
生活中存在的对数问题:
截止到1999年底,我国人口约13亿,如果今后能将人口平均增长水平控制在1%,经过多少年,我国人口数约16亿?
每个细胞分裂一次得到2个细胞,那一个细胞分裂多少次能得到1024个细胞?
……
某种细胞分裂时,得到的细胞的个
数y是分裂次数x的函数,这个函数可
以用指数函数y=2x表示.
分裂次数x就是要得到的细胞个
数y的函数.这个函数写成对数的形
式是x=log2y.
这种细胞经过多少次分裂,大约
可以得到1万个,10万个……细胞
x=log2y
x=log2y
如果用x表示自变量,y表示函
数,这个函数就是y=log2x.
对数函数
一.对数函数的定义
形如 的函数叫做对数函数,其中x是自变量,定义域是(0,+ )。
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:
(1)
(2)
2 对数函数对底数的限制:
且
例1求下列函数的定义域:
(1)
讲解范例
(2)
分析:求函数定义域时应从哪些方面来考虑?
函数研究流程图
列
表
作
图
观
察
图象特征
函数性质
二.对数函数的图像
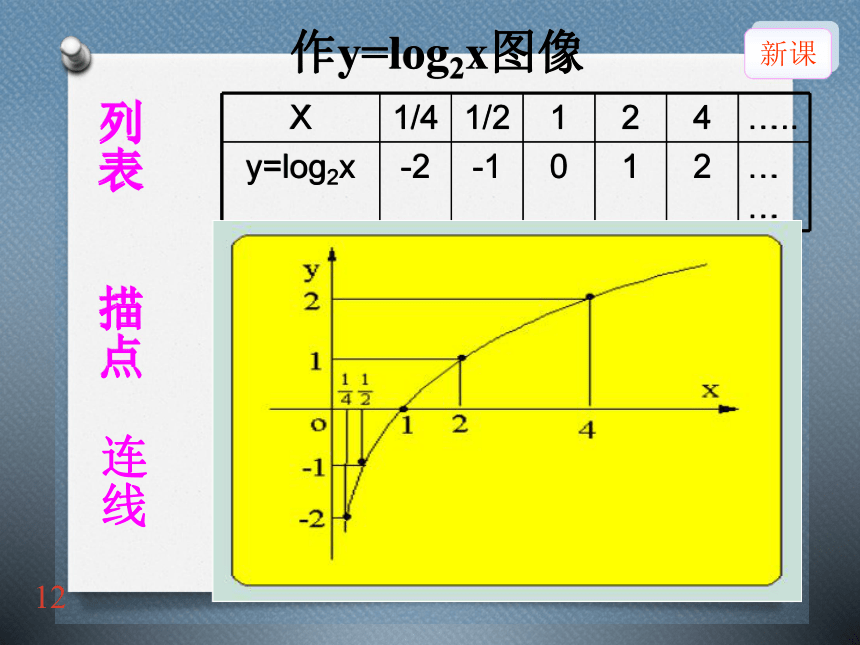
X 1/4 1/2 1 2 4 …..
y=log2x -2 -1 0 1 2 ……
列表
描点
作y=log2x图像
新课
12
连线
用几何画板作图
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
列表、求对应的x和y值、描点作图
1
二.对数函数的图像
x
0
1
y
(0x
0
1
y
(0x
0
1
y
(0x
0
1
y
(0x
0
1
y
(0x
0
1
y
(0x
0
1
y
(0x
0
1
y
(0x
0
1
y
(00
1
y
(a>1)
x
非奇非偶
奇偶性
(1,0)
定点
R
值域
定义域
大
致
图
形
三.对数函数的性质
y
x
0
1
y
(00
1
(a>1)
x
若00
若01则y<0
若a>1, x>1则y>0
若a>1, 0数值
变化
y=logax在(0,+ )上单调递减。
y=logax在(0,+ )上单调递增。
单调性
0a>1
大
致
图
形
x
0
1
y
x
0
1
y
例2
讲解范例
解(1)
解(2)
比较下列各组数中两个值的大小:
考查对数函数
因为它的底数2>1,所以它在
(0,+∞)上是增函数,因为3.4<8.5,于是
考查对数函数
因为它的底数0<0.3<1,所以它在
(0,+∞)上是减函数,又因为1.8<2.7,于是
(1)
(2)
(3)
且
解(3) 当a>1时,以为函数y=logax在(0, +∞)上是增函数,且5.1<5.9,所以loga5.1当0loga5.9
(4)
(5)
分析(4):
(5):
小 结
1. 两个同底数的对数比较大小的一般
步骤:
①确定所要考查的对数函数;
②根据对数底数判断对数函数增减性;
③比较真数大小,然后利用对数函数
的增减性判断两对数值的大小.
2. 分类讨论的思想.
3.找桥梁(常用桥梁1或0)
. 类比指数函数图象和性质的研究研究对数函数的性质:
底数a互为倒数的两个对数函数的图像有什么关系?
思考底数a是如何影响函数 的呢
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
用几何画板演示
底数互为倒数的两个对数函数的图像关于x轴对称。怎么用数学语言来说明?下节课你来告诉我们?
(提示:换底公式)
如果我们知道了 的图象,怎么 做 的 图象
思考底数a是如何影响函数 y=logax的呢
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
用几何画板演示
练一练:
x
y
0
1
y=log a x
y=log b x
y=log c x
y=log d x
比较a、b、c、d、1的大小。
答:b>a>1>d>c
底数a>1时,底数越大,其图像越接近x轴。
底数0在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
补充性质二
底数互为倒数的两个对数函数的图像关于x轴对称。
补充性质一
图
形
1
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
1788年前 澳洲大陆没有兔子
1788年 欧洲兔子来了,没人知道,
可怕的扩张开始
1890年 估计有4000万只兔子
1926年 达到创记录的100亿只兔子
人兔之战
解决方案
方案优点
实际效果
数学模型
人兔之战
生物防治:粘液瘤病毒;
兔子死亡率达到99.9%
蚊子传播,人畜无害;
1952年,澳洲约95%
的兔子种群被消灭
函数性质应用
1)、计算人体血液的pH值,并思考血液氢离子浓度与酸碱度之间的变化关系;
数学应用:
溶液中pH值的计算公式为pH= ,其中[H+]表示溶液中氢离子
的浓度,单位是摩尔/升。已知人体血液中氢离子浓度为[H+]=10-7.3摩尔/升。
2)、研究表明:粘液瘤病毒适合在血液pH值小于 中存活,
讨论粘液瘤病毒对人体是否有害。
小结 :
1.对数函数的定义:
函数
叫做对数函数;
的定义域为
值域为
小结 :
a>1 0图 象
性 质 定义域:
值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
2.对数函数的图象和性质
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
底数a>1时,底数越大,其图像越接近x轴。
底数0在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
补充性质二
底数互为倒数的两个对数函数的图像关于x轴对称。
补充性质一
图
形
1
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
3.思想、方法总结
归纳法、类比法
分类讨论、数形结合
给我一个支点和一个杆秆,我就能翘起地球。 ——阿基米德
如果我们找到兴趣和方法,我们就一定能够享受到数学带来的乐趣!一起努力吧!
给我空间、时间和对数,我可以创造宇宙。
——伽利略
生活中存在的对数问题:
截止到1999年底,我国人口约13亿,如果今后能将人口平均增长水平控制在1%,经过多少年,我国人口数约16亿?
每个细胞分裂一次得到2个细胞,那一个细胞分裂多少次能得到1024个细胞?
……
某种细胞分裂时,得到的细胞的个
数y是分裂次数x的函数,这个函数可
以用指数函数y=2x表示.
分裂次数x就是要得到的细胞个
数y的函数.这个函数写成对数的形
式是x=log2y.
这种细胞经过多少次分裂,大约
可以得到1万个,10万个……细胞
x=log2y
x=log2y
如果用x表示自变量,y表示函
数,这个函数就是y=log2x.
对数函数
一.对数函数的定义
形如 的函数叫做对数函数,其中x是自变量,定义域是(0,+ )。
注意:1 对数函数的定义与指数函数类似,都是形式定义,注意辨别.如:
(1)
(2)
2 对数函数对底数的限制:
且
例1求下列函数的定义域:
(1)
讲解范例
(2)
分析:求函数定义域时应从哪些方面来考虑?
函数研究流程图
列
表
作
图
观
察
图象特征
函数性质
二.对数函数的图像
X 1/4 1/2 1 2 4 …..
y=log2x -2 -1 0 1 2 ……
列表
描点
作y=log2x图像
新课
12
连线
用几何画板作图
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
列表、求对应的x和y值、描点作图
1
二.对数函数的图像
x
0
1
y
(0
0
1
y
(0
0
1
y
(0
0
1
y
(0
0
1
y
(0
0
1
y
(0
0
1
y
(0
0
1
y
(0
0
1
y
(0
1
y
(a>1)
x
非奇非偶
奇偶性
(1,0)
定点
R
值域
定义域
大
致
图
形
三.对数函数的性质
y
x
0
1
y
(0
1
(a>1)
x
若0
若0
若a>1, x>1则y>0
若a>1, 0
变化
y=logax在(0,+ )上单调递减。
y=logax在(0,+ )上单调递增。
单调性
0
大
致
图
形
x
0
1
y
x
0
1
y
例2
讲解范例
解(1)
解(2)
比较下列各组数中两个值的大小:
考查对数函数
因为它的底数2>1,所以它在
(0,+∞)上是增函数,因为3.4<8.5,于是
考查对数函数
因为它的底数0<0.3<1,所以它在
(0,+∞)上是减函数,又因为1.8<2.7,于是
(1)
(2)
(3)
且
解(3) 当a>1时,以为函数y=logax在(0, +∞)上是增函数,且5.1<5.9,所以loga5.1
(4)
(5)
分析(4):
(5):
小 结
1. 两个同底数的对数比较大小的一般
步骤:
①确定所要考查的对数函数;
②根据对数底数判断对数函数增减性;
③比较真数大小,然后利用对数函数
的增减性判断两对数值的大小.
2. 分类讨论的思想.
3.找桥梁(常用桥梁1或0)
. 类比指数函数图象和性质的研究研究对数函数的性质:
底数a互为倒数的两个对数函数的图像有什么关系?
思考底数a是如何影响函数 的呢
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
用几何画板演示
底数互为倒数的两个对数函数的图像关于x轴对称。怎么用数学语言来说明?下节课你来告诉我们?
(提示:换底公式)
如果我们知道了 的图象,怎么 做 的 图象
思考底数a是如何影响函数 y=logax的呢
规律:在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大.
用几何画板演示
练一练:
x
y
0
1
y=log a x
y=log b x
y=log c x
y=log d x
比较a、b、c、d、1的大小。
答:b>a>1>d>c
底数a>1时,底数越大,其图像越接近x轴。
底数0
补充性质二
底数互为倒数的两个对数函数的图像关于x轴对称。
补充性质一
图
形
1
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
1788年前 澳洲大陆没有兔子
1788年 欧洲兔子来了,没人知道,
可怕的扩张开始
1890年 估计有4000万只兔子
1926年 达到创记录的100亿只兔子
人兔之战
解决方案
方案优点
实际效果
数学模型
人兔之战
生物防治:粘液瘤病毒;
兔子死亡率达到99.9%
蚊子传播,人畜无害;
1952年,澳洲约95%
的兔子种群被消灭
函数性质应用
1)、计算人体血液的pH值,并思考血液氢离子浓度与酸碱度之间的变化关系;
数学应用:
溶液中pH值的计算公式为pH= ,其中[H+]表示溶液中氢离子
的浓度,单位是摩尔/升。已知人体血液中氢离子浓度为[H+]=10-7.3摩尔/升。
2)、研究表明:粘液瘤病毒适合在血液pH值小于 中存活,
讨论粘液瘤病毒对人体是否有害。
小结 :
1.对数函数的定义:
函数
叫做对数函数;
的定义域为
值域为
小结 :
a>1 0
性 质 定义域:
值域:
在(0,+∞)上是 函数 在(0,+∞)上是 函数
2.对数函数的图象和性质
(0,+∞)
过点(1,0),即当x=1时,y=0
增
减
底数a>1时,底数越大,其图像越接近x轴。
底数0
补充性质二
底数互为倒数的两个对数函数的图像关于x轴对称。
补充性质一
图
形
1
0.5
y=log x
0.1
y=log x
10
y=log x
2
y=log x
0
x
y
3.思想、方法总结
归纳法、类比法
分类讨论、数形结合
给我一个支点和一个杆秆,我就能翘起地球。 ——阿基米德
如果我们找到兴趣和方法,我们就一定能够享受到数学带来的乐趣!一起努力吧!
