人教版七年级上册第四章 几何图形初步4.2.2 线段长短的比较与运算 课后练习(word版含解析)
文档属性
| 名称 | 人教版七年级上册第四章 几何图形初步4.2.2 线段长短的比较与运算 课后练习(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 08:39:33 | ||
图片预览

文档简介
4.2.2线段长短的比较与运算
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.如图,点C、D为线段AB上两点,AC+BD=6,且AD+BCAB,则CD等于( )
A.10 B.8 C.6 D.4
2.如图,已知线段AB=10cm,M是AB中点,点N在AB上,MN=3cm,那么线段NB的长为( )
A.2cm B.3cm C.5cm D.8cm
3.如图AB=CD,则AC与BD的大小关系是()
A.AC>BD B.AC<BD C.AC=BD D.无法确定
4.如图,点C为线段AB的中点,点D为线段AC的中点、已知AB=8,则BD=()
A.2 B.4 C.6 D.8
5.如果点B在线段AC上,那么下列表达式中:①AB=AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有()
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题6分,共30分)
6.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出“人们喜欢抄近路”这一现象的原因是______________________________.
7.已知点P是线段AB的中点,若AB=6cm,则PB=cm.
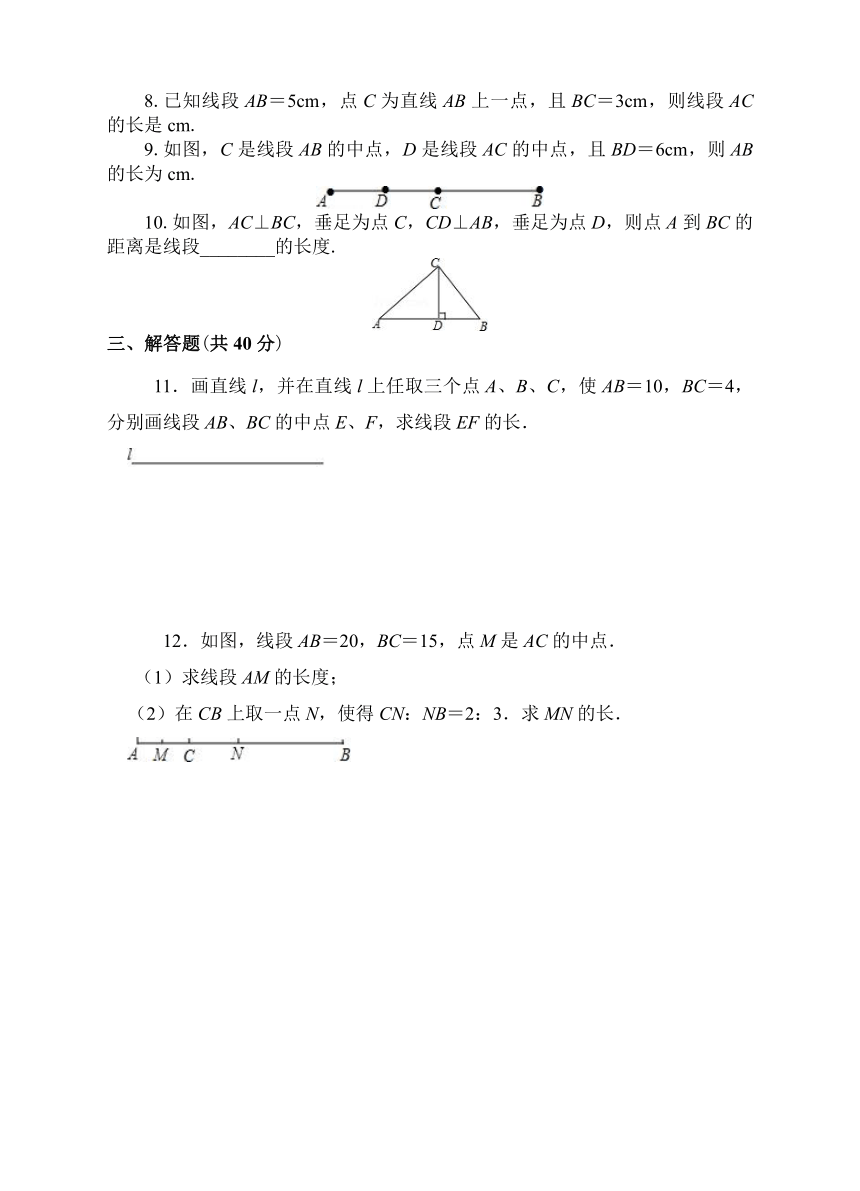
8.已知线段AB=5cm,点C为直线AB上一点,且BC=3cm,则线段AC的长是cm.
9.如图,C是线段AB的中点,D是线段AC的中点,且BD=6cm,则AB的长为cm.
10.如图,AC⊥BC,垂足为点C,CD⊥AB,垂足为点D,则点A到BC的距离是线段________的长度.
三、解答题(共40分)
11.画直线l,并在直线l上任取三个点A、B、C,使AB=10,BC=4,分别画线段AB、BC的中点E、F,求线段EF的长.
12.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
参考答案
1.D
【解析】∵AD+BCAB,
∴5(AD+BC)=7AB,
∴5(AC+CD+CD+BD)=7(AC+CD+BD),
∵AC+BD=6,
∴CD=4,
故选:D.
2.A
【解析】∵AB=10cm,M是AB中点,
∴BMAB=5cm,
又∵MN=3cm,
∴NB=BM﹣MN=5﹣3=2(cm).
故选:A.
3.C.
【解析】根据AB=CD两边都加上线段BC得出AB+BC=CD+BC,即可得出答案.
解:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故选C.
4.C
【解析】根据两中点进行解答.
解:∵点C为线段AB的中点,AB=8,则BC=AC=4.
点D为线段AC的中点,则AD=DC=2.
∴BD=CD+BC=6.
故选C.
5.C
【解析】根据题意,画出图形,观察图形,一一分析选项,排除错误答案.
解:如图,若B是线段AC的中点,
则AB=AC,AB=BC,AC=2AB,
而AB+BC=AC,B可是线段AC上的任意一点,
∴表示B是线段AC的中点的有①②③3个.
故选C.
6.两点之间线段最短.
【解析】为抄近路践踏草坪原因是:两点之间线段最短.故答案为:两点之间线段最短.
7.3
【解析】根据线段的中点平分线段的长度.根据点P是线段AB的中点,则PB=AB==3cm.
8.2cm或8cm.
【解析】本题有两种情形:①当点C在线段AB上时,如图1,AC=AB-BC=5-3=2cm;②当点C在线段AB的延长线上时,如图2,AC=AB+BC=5+3=8cm.综上可得:AC=2cm或8cm.
9.8
【解析】根据线段中点的性质,可得DC与AC的关系,BC与AC的关系,根据线段的和差,可得BC的长,可得答案.
解:由C是线段AB的中点,D是线段AC的中点,得
AB=2BC=2AC,CD=AC=BC.
由线段的和差,得
BD=BC+CD,即
BC+BC=6,
解得BC=4.
AB=2BC=8cm.
故答案为:8.
10.AC
【解析】根据点到直线的距离是直线外的点到直线的垂线段的长度,可得答案.
解:AC⊥BC,垂足为点C,CD⊥AB,垂足为点D,则点A到BC的距离是线段AC的长度,
故答案为:AC.
11.画直线l,并在直线l上任取三个点A、B、C,使AB=10,BC=4,分别画线段AB、BC的中点E、F,求线段EF的长.
【分析】根据线段中点的定义和线段的和差即可得到结论.
【解析】因为点E、F分别是线段AB、BC的中点,
所以,;
第一种:点C在点B的右侧,
因为 EF=BE+BF,
所以;
第二种:点C在点B的左侧,
因为 EF=BE﹣BF,
所以.
综上:EF=7或3.
12.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
【分析】(1)根据图示知AMAC,AC=AB﹣BC;
(2)根据已知条件求得CN=6,然后根据图示知MN=MC+NC.
【解析】(1)线段AB=20,BC=15,
∴AC=AB﹣BC=20﹣15=5.
又∵点M是AC的中点.
∴AMAC5,即线段AM的长度是.
(2)∵BC=15,CN:NB=2:3,
∴CNBC15=6.
又∵点M是AC的中点,AC=5,
∴MCAC,
∴MN=MC+NC,即MN的长度是.
班级:___________姓名:___________得分:___________
一、选择题(每小题6分,共30分)
1.如图,点C、D为线段AB上两点,AC+BD=6,且AD+BCAB,则CD等于( )
A.10 B.8 C.6 D.4
2.如图,已知线段AB=10cm,M是AB中点,点N在AB上,MN=3cm,那么线段NB的长为( )
A.2cm B.3cm C.5cm D.8cm
3.如图AB=CD,则AC与BD的大小关系是()
A.AC>BD B.AC<BD C.AC=BD D.无法确定
4.如图,点C为线段AB的中点,点D为线段AC的中点、已知AB=8,则BD=()
A.2 B.4 C.6 D.8
5.如果点B在线段AC上,那么下列表达式中:①AB=AC,②AB=BC,③AC=2AB,④AB+BC=AC,能表示B是线段AC的中点的有()
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题6分,共30分)
6.如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出“人们喜欢抄近路”这一现象的原因是______________________________.
7.已知点P是线段AB的中点,若AB=6cm,则PB=cm.
8.已知线段AB=5cm,点C为直线AB上一点,且BC=3cm,则线段AC的长是cm.
9.如图,C是线段AB的中点,D是线段AC的中点,且BD=6cm,则AB的长为cm.
10.如图,AC⊥BC,垂足为点C,CD⊥AB,垂足为点D,则点A到BC的距离是线段________的长度.
三、解答题(共40分)
11.画直线l,并在直线l上任取三个点A、B、C,使AB=10,BC=4,分别画线段AB、BC的中点E、F,求线段EF的长.
12.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
参考答案
1.D
【解析】∵AD+BCAB,
∴5(AD+BC)=7AB,
∴5(AC+CD+CD+BD)=7(AC+CD+BD),
∵AC+BD=6,
∴CD=4,
故选:D.
2.A
【解析】∵AB=10cm,M是AB中点,
∴BMAB=5cm,
又∵MN=3cm,
∴NB=BM﹣MN=5﹣3=2(cm).
故选:A.
3.C.
【解析】根据AB=CD两边都加上线段BC得出AB+BC=CD+BC,即可得出答案.
解:∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故选C.
4.C
【解析】根据两中点进行解答.
解:∵点C为线段AB的中点,AB=8,则BC=AC=4.
点D为线段AC的中点,则AD=DC=2.
∴BD=CD+BC=6.
故选C.
5.C
【解析】根据题意,画出图形,观察图形,一一分析选项,排除错误答案.
解:如图,若B是线段AC的中点,
则AB=AC,AB=BC,AC=2AB,
而AB+BC=AC,B可是线段AC上的任意一点,
∴表示B是线段AC的中点的有①②③3个.
故选C.
6.两点之间线段最短.
【解析】为抄近路践踏草坪原因是:两点之间线段最短.故答案为:两点之间线段最短.
7.3
【解析】根据线段的中点平分线段的长度.根据点P是线段AB的中点,则PB=AB==3cm.
8.2cm或8cm.
【解析】本题有两种情形:①当点C在线段AB上时,如图1,AC=AB-BC=5-3=2cm;②当点C在线段AB的延长线上时,如图2,AC=AB+BC=5+3=8cm.综上可得:AC=2cm或8cm.
9.8
【解析】根据线段中点的性质,可得DC与AC的关系,BC与AC的关系,根据线段的和差,可得BC的长,可得答案.
解:由C是线段AB的中点,D是线段AC的中点,得
AB=2BC=2AC,CD=AC=BC.
由线段的和差,得
BD=BC+CD,即
BC+BC=6,
解得BC=4.
AB=2BC=8cm.
故答案为:8.
10.AC
【解析】根据点到直线的距离是直线外的点到直线的垂线段的长度,可得答案.
解:AC⊥BC,垂足为点C,CD⊥AB,垂足为点D,则点A到BC的距离是线段AC的长度,
故答案为:AC.
11.画直线l,并在直线l上任取三个点A、B、C,使AB=10,BC=4,分别画线段AB、BC的中点E、F,求线段EF的长.
【分析】根据线段中点的定义和线段的和差即可得到结论.
【解析】因为点E、F分别是线段AB、BC的中点,
所以,;
第一种:点C在点B的右侧,
因为 EF=BE+BF,
所以;
第二种:点C在点B的左侧,
因为 EF=BE﹣BF,
所以.
综上:EF=7或3.
12.如图,线段AB=20,BC=15,点M是AC的中点.
(1)求线段AM的长度;
(2)在CB上取一点N,使得CN:NB=2:3.求MN的长.
【分析】(1)根据图示知AMAC,AC=AB﹣BC;
(2)根据已知条件求得CN=6,然后根据图示知MN=MC+NC.
【解析】(1)线段AB=20,BC=15,
∴AC=AB﹣BC=20﹣15=5.
又∵点M是AC的中点.
∴AMAC5,即线段AM的长度是.
(2)∵BC=15,CN:NB=2:3,
∴CNBC15=6.
又∵点M是AC的中点,AC=5,
∴MCAC,
∴MN=MC+NC,即MN的长度是.
