2013高一数学必修1课件:3.2.1 第二课时 换底公式与自然对数(新人教B版)
文档属性
| 名称 | 2013高一数学必修1课件:3.2.1 第二课时 换底公式与自然对数(新人教B版) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-11 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
3.2
对数与对数函数
3.2.1
对
数
及
其
运
算
把握热点考向
应用创新演练
第三章
基本初等函数(Ⅰ)
考点一
考点二
第二课时
换底公式与自然对数
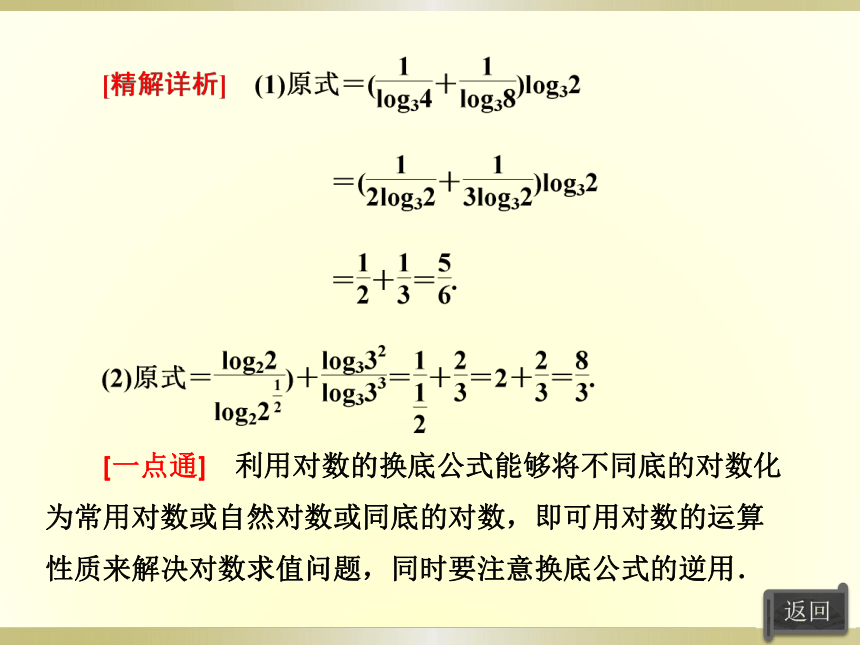
[例1] 计算下列各式的值:
(1)(log43+log83)log32;
(2)log 2+log279.
[思路点拨] 先用换底公式化为同底的对数,再运用运算性质运算.
[一点通] 利用对数的换底公式能够将不同底的对数化为常用对数或自然对数或同底的对数,即可用对数的运算性质来解决对数求值问题,同时要注意换底公式的逆用.
答案:A
3.已知log62=p,log65=q,则lg 5=__________.(用p,
q表示)
[思路点拨] 先求出x,y,z的表达式,即将已知指数式化为对数式,然后求解和证明.
[一点通] 对数式的证明和对数式的化简的基本思路是一致的,就是根据对数的运算性质和换底公式对对数式化简.
4.解方程(lg x)2+lg x3-10=0.
解:原方程变形为
(lg x)2+3lg x-10=0,
即(lg x+5)(lg x-2)=0,
∴lg x=-5或lg x=2,
∴x=10-5或x=100.
经检验知:x=10-5和x=100都是原方程的根.
6.如果方程(lg x)2+(lg 7+lg 5)lg x+lg 7·lg 5=0的两根是
α,β,求αβ的值.
(1)换底公式主要用于计算、化简求值,用于计算时把底统一化成以10为底的对数.化简时,有两种思路:①根据题目特点,先换部分对数的底进行运算,最后再得结果;②直接把题中对数全换成同一底的对数进行运算.
3.2
对数与对数函数
3.2.1
对
数
及
其
运
算
把握热点考向
应用创新演练
第三章
基本初等函数(Ⅰ)
考点一
考点二
第二课时
换底公式与自然对数
[例1] 计算下列各式的值:
(1)(log43+log83)log32;
(2)log 2+log279.
[思路点拨] 先用换底公式化为同底的对数,再运用运算性质运算.
[一点通] 利用对数的换底公式能够将不同底的对数化为常用对数或自然对数或同底的对数,即可用对数的运算性质来解决对数求值问题,同时要注意换底公式的逆用.
答案:A
3.已知log62=p,log65=q,则lg 5=__________.(用p,
q表示)
[思路点拨] 先求出x,y,z的表达式,即将已知指数式化为对数式,然后求解和证明.
[一点通] 对数式的证明和对数式的化简的基本思路是一致的,就是根据对数的运算性质和换底公式对对数式化简.
4.解方程(lg x)2+lg x3-10=0.
解:原方程变形为
(lg x)2+3lg x-10=0,
即(lg x+5)(lg x-2)=0,
∴lg x=-5或lg x=2,
∴x=10-5或x=100.
经检验知:x=10-5和x=100都是原方程的根.
6.如果方程(lg x)2+(lg 7+lg 5)lg x+lg 7·lg 5=0的两根是
α,β,求αβ的值.
(1)换底公式主要用于计算、化简求值,用于计算时把底统一化成以10为底的对数.化简时,有两种思路:①根据题目特点,先换部分对数的底进行运算,最后再得结果;②直接把题中对数全换成同一底的对数进行运算.
