2013高一数学必修1课件:3.1.2 指数函数(新人教B版)
文档属性
| 名称 | 2013高一数学必修1课件:3.1.2 指数函数(新人教B版) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-11 00:00:00 | ||
图片预览











文档简介
(共49张PPT)
3.1
指数与指数函数
3.1.2
指
数
函
数
理解教材新知
把握热点考向
应用创新演练
第三章
基本初等函数(Ⅰ)
知识点一
考点一
考点二
考点三
知识点二
考点四
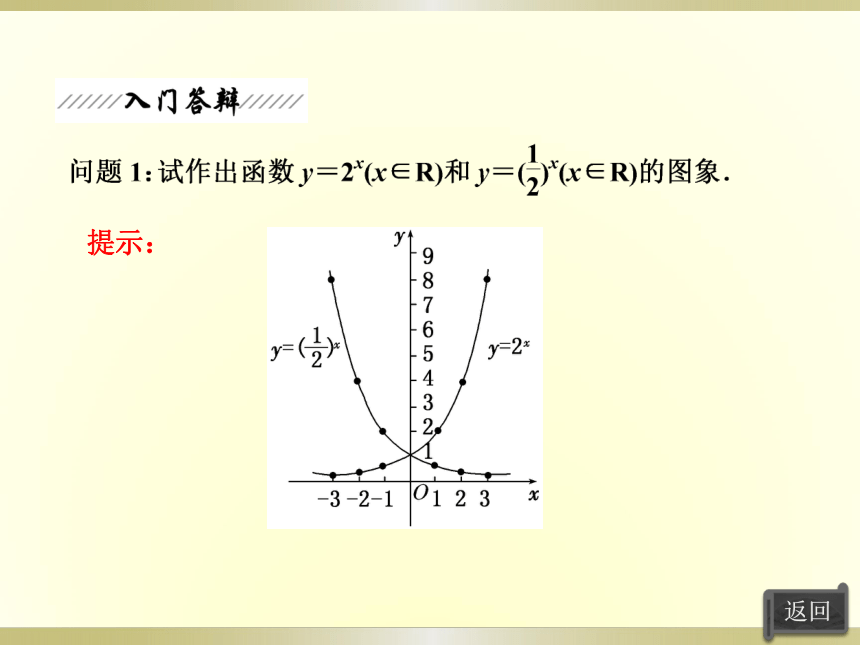
某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量就变为原来的84%.假设这种物质原来的质量为1.
问题1:经过3年这种物质的质量是多少?
提示:0.843.
问题2:若经过x年后质量为y,则y与x的关系能用等式表示吗?
提示:能,y=0.84x.
问题3:质量y是经过年数x(x>0)的函数吗?
提示:是,符合函数的定义.
问题4:如果不考虑x、y的实际意义,x∈R时等式y=0.84x是否表示y是x的函数?如果是,该函数有何特点?
提示:是.底数是常数,指数是自变量.
指数函数的定义
函数 叫做指数函数,其中x是自变量,函数的定义域为R.
y=ax(a>0且a≠1)
提示:
问题2:两函数图象有无交点?
提示:有交点,其坐标为(0,1).
问题3:两函数的定义域是什么?值域是什么?单调性如何?
a>1 0<a<1
图 象
性 质 定义域
值域
过定点 过点 ,即x= 时,y=
单调性 是R上的 是R上的
R
(0,+∞)
(0,1)
0
1
增函数
减函数
指数函数的图象和性质
(1)指数函数中,底数是一个常量,自变量出现在指数位置上.显然y=xa不是指数函数,这一点要特别注意.
(2)指数函数中,系数一定为1,指数一定为x.例如,
y=3·2x不是指数函数,y=2x+1也不是指数函数.
(3)当01时,x→-∞,y→0. (其中“x→+∞”的意义是“x接近于正无穷大”)
[例1] 下列函数中,哪些是指数函数?
(1)y=10x;(2)y=10x+1;(3)y=-4x;
(4)y=xx;(5)y=xα(α是常数).
[思路点拨] 解答本题的关键是理解指数函数的定义,即只有符合y=ax(a>0且a≠1,x∈R)的函数才是指数函数,否则不是.
[精解详析] (1)y=10x符合定义,是指数函数;
(2)y=10x+1中指数是x+1而非x,不是指数函数;
(3)y=-4x中系数为-1而非1,不是指数函数;
(4)y=xx中底数和指数均是自变量x,不符合指数函数定义,不是指数函数;
(5)y=xα中底数是自变量,不是指数函数.
[一点通] 判定一个函数为指数函数:①底数要大于零且不等于1;②幂指数是自变量x;③系数为1,是y=ax(a>0,a≠1,x∈R)这样的形式.
答案:③
2.若函数y=(a2-3a+3)·ax是指数函数,求a的值.
[思路点拨] 函数y=ax的图象过点(1,a),可根据各图象上横坐标为1的点的位置确定a的大小.
[一点通]
(1)指数函数的图象随底数变化的规律:
①无论指数函数的底数a如何变化,指数函数y=ax的图像都与直线x=1相交于点(1,a),由图像可知:在y轴右侧,图象从下到上相应的底数由小变大.
②指数函数的底数与图象间的关系可概括记忆为:在第一象限内,图高则底大.
(2) 指数函数图象问题的处理方法
①抓住图象上的特殊点,如指数函数的图象过定点(0,1);
②利用图象变换,如函数图象的平移变换(左右平移、上下平移);
③利用函数的奇偶性与单调性.
3.函数y=2-|x|的大致图象是 ( )
答案:C
4.函数f(x)=ax-1+1(a>0且a≠1)的图像过定点A,则A点的
坐标为________.
解析:原函数f(x)=ax-1+1可变形为y-1=ax-1,将y-1看做x-1的函数.
令x-1=0,则y-1=1,即x=1,y=2,
∴函数f(x)=ax-1+1的图象恒过定点A(1,2).
答案:(1,2)
[精解详析] (1)1.82.2,1.83可看做函数y=1.8x的两个函数值,
∵1.8>1,∴y=1.8x在R上为增函数.
∴1.82.2<1.83.
(2)∵y=0.7x在R上为减函数,
又∵-0.3>-0.4,∴0.7-0.3<0.7-0.4.
(3)∵1.90.4>1.90=1,0.92.4<0.90=1,
∴1.90.4>0.92.4.
[一点通] 比较幂的大小的方法:
(1)对于底数相同但指数不同的幂,可以利用指数函数的单调性来比较.
(2)对于底数不同但指数相同的幂,可利用指数函数图象的变化规律来比较.
(3)对于底数不同且指数不同的幂,则应通过中间值来比较.
解析:函数y=0.9x在R上为减函数,所以0.90.3>0.90.5.
答案:D
答案:m8.如果a-5x>ax+7(a>0,且a≠1),求x的取值范围.
[思路点拨] 确保指数有意义,可得其定义域,再由定义域确定值域.
(3)定义域为R.
∵2x-x2=-(x-1)2+1≤1,? (10分)
∴22x-x2≤2,即y≤2.
故函数的值域为(0,2].? (12分)
[一点通] (1)函数y=af(x)的定义域与y=f(x)的定义域相同.
(2)函数y=af(x)的值域的求法如下:
①换元,令t=f(x);
②求t=f(x)的定义域x∈D;
③求t=f(x)的值域t∈M;
④利用y=at的单调性求y=at,t∈M的值域.
解析:由题意知ax≥1的解集是(-∞,0],∴0答案:(0,1)
(1)应用指数函数y=ax的单调性时,如果底数a大小不确定,必须分“a>1”和“0(2)当a>1时,a的值越大,图象越靠近y轴,递增速度越快.当0
3.1
指数与指数函数
3.1.2
指
数
函
数
理解教材新知
把握热点考向
应用创新演练
第三章
基本初等函数(Ⅰ)
知识点一
考点一
考点二
考点三
知识点二
考点四
某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量就变为原来的84%.假设这种物质原来的质量为1.
问题1:经过3年这种物质的质量是多少?
提示:0.843.
问题2:若经过x年后质量为y,则y与x的关系能用等式表示吗?
提示:能,y=0.84x.
问题3:质量y是经过年数x(x>0)的函数吗?
提示:是,符合函数的定义.
问题4:如果不考虑x、y的实际意义,x∈R时等式y=0.84x是否表示y是x的函数?如果是,该函数有何特点?
提示:是.底数是常数,指数是自变量.
指数函数的定义
函数 叫做指数函数,其中x是自变量,函数的定义域为R.
y=ax(a>0且a≠1)
提示:
问题2:两函数图象有无交点?
提示:有交点,其坐标为(0,1).
问题3:两函数的定义域是什么?值域是什么?单调性如何?
a>1 0<a<1
图 象
性 质 定义域
值域
过定点 过点 ,即x= 时,y=
单调性 是R上的 是R上的
R
(0,+∞)
(0,1)
0
1
增函数
减函数
指数函数的图象和性质
(1)指数函数中,底数是一个常量,自变量出现在指数位置上.显然y=xa不是指数函数,这一点要特别注意.
(2)指数函数中,系数一定为1,指数一定为x.例如,
y=3·2x不是指数函数,y=2x+1也不是指数函数.
(3)当0
[例1] 下列函数中,哪些是指数函数?
(1)y=10x;(2)y=10x+1;(3)y=-4x;
(4)y=xx;(5)y=xα(α是常数).
[思路点拨] 解答本题的关键是理解指数函数的定义,即只有符合y=ax(a>0且a≠1,x∈R)的函数才是指数函数,否则不是.
[精解详析] (1)y=10x符合定义,是指数函数;
(2)y=10x+1中指数是x+1而非x,不是指数函数;
(3)y=-4x中系数为-1而非1,不是指数函数;
(4)y=xx中底数和指数均是自变量x,不符合指数函数定义,不是指数函数;
(5)y=xα中底数是自变量,不是指数函数.
[一点通] 判定一个函数为指数函数:①底数要大于零且不等于1;②幂指数是自变量x;③系数为1,是y=ax(a>0,a≠1,x∈R)这样的形式.
答案:③
2.若函数y=(a2-3a+3)·ax是指数函数,求a的值.
[思路点拨] 函数y=ax的图象过点(1,a),可根据各图象上横坐标为1的点的位置确定a的大小.
[一点通]
(1)指数函数的图象随底数变化的规律:
①无论指数函数的底数a如何变化,指数函数y=ax的图像都与直线x=1相交于点(1,a),由图像可知:在y轴右侧,图象从下到上相应的底数由小变大.
②指数函数的底数与图象间的关系可概括记忆为:在第一象限内,图高则底大.
(2) 指数函数图象问题的处理方法
①抓住图象上的特殊点,如指数函数的图象过定点(0,1);
②利用图象变换,如函数图象的平移变换(左右平移、上下平移);
③利用函数的奇偶性与单调性.
3.函数y=2-|x|的大致图象是 ( )
答案:C
4.函数f(x)=ax-1+1(a>0且a≠1)的图像过定点A,则A点的
坐标为________.
解析:原函数f(x)=ax-1+1可变形为y-1=ax-1,将y-1看做x-1的函数.
令x-1=0,则y-1=1,即x=1,y=2,
∴函数f(x)=ax-1+1的图象恒过定点A(1,2).
答案:(1,2)
[精解详析] (1)1.82.2,1.83可看做函数y=1.8x的两个函数值,
∵1.8>1,∴y=1.8x在R上为增函数.
∴1.82.2<1.83.
(2)∵y=0.7x在R上为减函数,
又∵-0.3>-0.4,∴0.7-0.3<0.7-0.4.
(3)∵1.90.4>1.90=1,0.92.4<0.90=1,
∴1.90.4>0.92.4.
[一点通] 比较幂的大小的方法:
(1)对于底数相同但指数不同的幂,可以利用指数函数的单调性来比较.
(2)对于底数不同但指数相同的幂,可利用指数函数图象的变化规律来比较.
(3)对于底数不同且指数不同的幂,则应通过中间值来比较.
解析:函数y=0.9x在R上为减函数,所以0.90.3>0.90.5.
答案:D
答案:m
[思路点拨] 确保指数有意义,可得其定义域,再由定义域确定值域.
(3)定义域为R.
∵2x-x2=-(x-1)2+1≤1,? (10分)
∴22x-x2≤2,即y≤2.
故函数的值域为(0,2].? (12分)
[一点通] (1)函数y=af(x)的定义域与y=f(x)的定义域相同.
(2)函数y=af(x)的值域的求法如下:
①换元,令t=f(x);
②求t=f(x)的定义域x∈D;
③求t=f(x)的值域t∈M;
④利用y=at的单调性求y=at,t∈M的值域.
解析:由题意知ax≥1的解集是(-∞,0],∴0
(1)应用指数函数y=ax的单调性时,如果底数a大小不确定,必须分“a>1”和“0
