2021-2022学年北师大版九年级数学下册《2.3 确定二次函数表达式》同步达标训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册《2.3 确定二次函数表达式》同步达标训练 (Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 194.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 00:00:00 | ||
图片预览





文档简介
2021-2022学年北师大版九年级数学下册《2.3确定二次函数表达式》
同步达标训练(附答案)
1.已知抛物线y=ax2+bx经过点A(﹣3,﹣3),且该抛物线的对称轴经过点A,则该抛物线的解析式为( )
A.y=﹣x2﹣2x B.y=﹣x2+2x C.y=x2﹣2x D.y=x2+2x
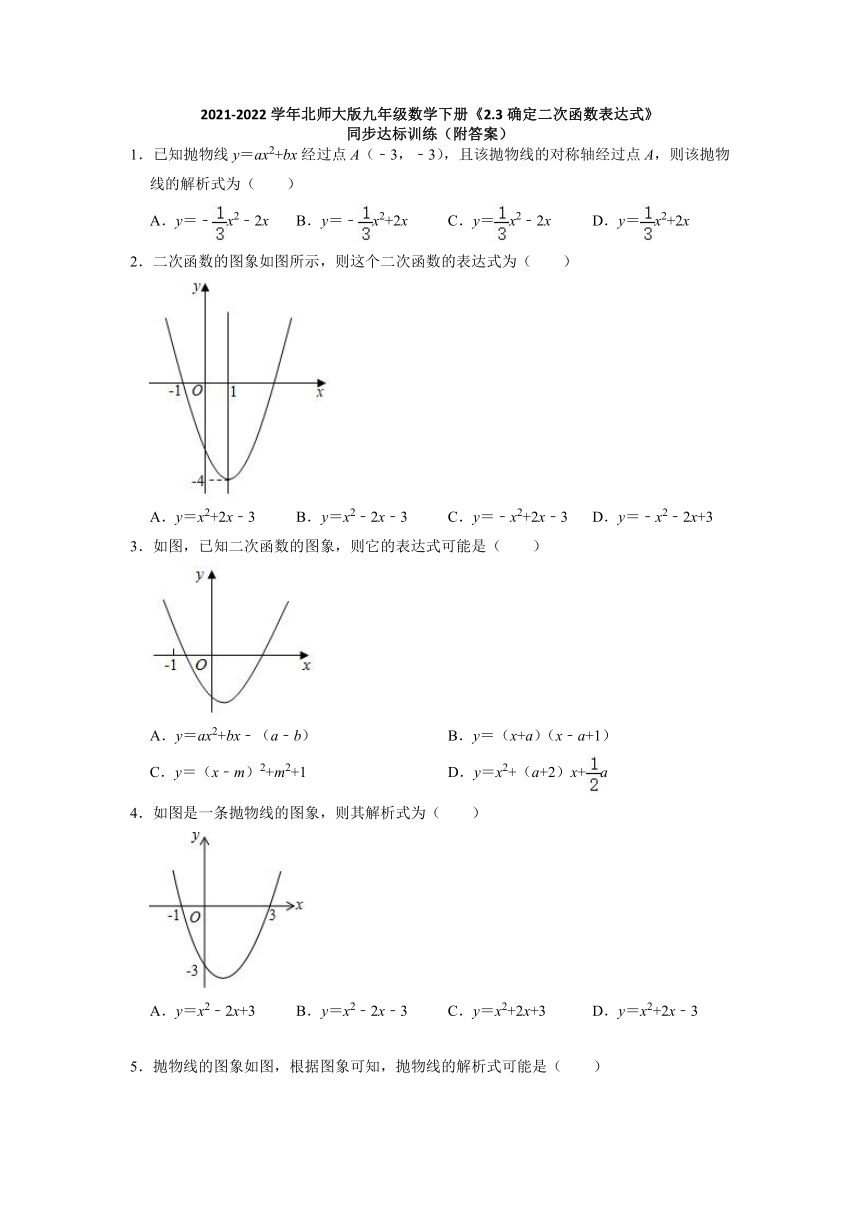
2.二次函数的图象如图所示,则这个二次函数的表达式为( )
A.y=x2+2x﹣3 B.y=x2﹣2x﹣3 C.y=﹣x2+2x﹣3 D.y=﹣x2﹣2x+3
3.如图,已知二次函数的图象,则它的表达式可能是( )
A.y=ax2+bx﹣(a﹣b) B.y=(x+a)(x﹣a+1)
C.y=(x﹣m)2+m2+1 D.y=x2+(a+2)x+a
4.如图是一条抛物线的图象,则其解析式为( )
A.y=x2﹣2x+3 B.y=x2﹣2x﹣3 C.y=x2+2x+3 D.y=x2+2x﹣3
5.抛物线的图象如图,根据图象可知,抛物线的解析式可能是( )
A.y=x2﹣x+2 B.y=﹣x2﹣x+2
C.y=﹣x2﹣x+1 D.y=﹣x2+x+2
6.已知抛物线与二次函数y=﹣5x2的图象相同,开口方向相同,且顶点坐标为(﹣1,2020),它对应的函数表达式为( )
A.y=﹣5(x﹣1) 2+2020 B.y=5(x﹣1) 2+2020
C.y=5(x+1) 2+2020 D.y=﹣5(x+1)2+2020
7.二次函数的图象如图所示,则其解析式是( )
A.y=﹣x2+2x+3 B.y=x2﹣2x﹣3 C.y=﹣x2﹣2x+3 D.y=﹣x2﹣2x﹣3
8.若|m+3|+=0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
A.y=(x﹣3)2+2 B.y=(x+3)2﹣2
C.y=(x﹣3)2﹣2 D.y=(x+3)2+2
9.当k取任意实数时,抛物线y=3(x﹣k﹣1)2+k2+2的顶点所在的函数图象的解析式是( )
A.y=x2+2 B.y=x2﹣2x+1 C.y=x2﹣2x+3 D.y=x2+2x﹣3
10.二次函数部分图象如图所示,对称轴是直线x=﹣1,则这个二次函数的表达式为( )
A.y=﹣x2+2x+3 B.y=x2+2x+3 C.y=﹣x2+2x﹣3 D.y=﹣x2﹣2x+3
11.小聪做作业时不小心将墨水滴在一道数学题上,题目变为:“已知二次函数y=x2□x□的图象如图所示”,则题目中二次函数的表达式为( )
A.y=x2+x﹣2 B.y=x2﹣x﹣2 C.y=x2+x+2 D.y=x2﹣x+2
12.已知抛物线y=﹣x2+bx+c,当1<x<3时,y值为正,当x<1或x>3时,y值为负,则抛物线的解析式为 .
13.已知一个二次函数的图象形状与抛物线y=4x2相同,且顶点坐标为(2,3),则这个二次函数的解析式为 .
14.如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的一个动点,过点C的直线与二次函数y=x2的图象交于A、B两点,且CB=3AC,P为CB的中点,设点P的坐标为P(x,y)(x>0),写出y关于x的函数表达式为: .
15.有一条抛物线,两位同学分别说了它的一个特点:
甲:对称轴是直线x=4;
乙:顶点到x轴的距离为2.
请你写出一个符合条件的解析式: .
16.已知一条抛物线具有以下特征:(1)经过原点;(2)在y轴左侧的部分,图象上升,在y轴右侧的部分,图象下降.试写出一个符合要求的抛物线的表达式: .
17.如图,平行四边形ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线经过x轴上的点A,B,则此抛物线的解析式为 .
18.在平面直角坐标系中,抛物线y=ax2+bx+3过点A(1,0)和B(2,﹣1).
(1)求二次函数的表达式;
(2)求二次函数图象的顶点坐标和对称轴.
19.如图,已知二次函数y=ax2+bx+c的图象过点A(﹣1,0)和点C(0,3),对称轴为直线x=1.
(1)求该二次函数的关系式和顶点坐标;
(2)结合图象,当y<3时,直接写出x的取值范围.
20.如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E,直线y=mx+n经过B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)点F是抛物线对称轴上一点,当FA+FC的值最小时,求出点F的坐标及FA+FC的最小值.
参考答案
1.解:∵抛物线y=ax2+bx经过点A(﹣3,﹣3),且抛物线的对称轴经过点A,
∴函数的顶点坐标是(﹣3,﹣3),
∴,
解得,
∴该抛物线的解析式为y=.
故选:D.
2.解:从图象可知:二次函数的顶点坐标是(1,﹣4),与x轴的交点坐标是(﹣1,0),
设二次函数的解析式是y=a(x﹣1)2﹣4,
把(﹣1,0)代入得:0=a(﹣1﹣1)2﹣4,
解得:a=1,
所以y=(x﹣1)2﹣4=x2﹣2x﹣3,
故选:B.
3.解:A、y=ax2+bx﹣(a﹣b)=(ax﹣a+b)(x+1),令(ax﹣a+b)(x+1)=0得x1=,x2=﹣1,即图象与x轴一个交点横坐标应等于﹣1,故A不符合题意;
B、令y=0得x1=﹣a,x2=a﹣1,若﹣1<﹣a<0,则0<a<1,可得﹣1<a﹣1<0,同理若﹣1<a﹣1<0,则可得﹣1<﹣a<0,即抛物线与x轴两个交点横坐标都在﹣1到0之间,故B不符合题意;
C、抛物线y=(x﹣m)2+m2+1顶点为(m,m2+1),而m2+1>0,顶点在x轴上方,故C不符合题意;
D、图象可能为y=x2+(a+2)x+a,故D符合题意.
故选:D.
4.解:因为抛物线与x轴的交点坐标为(﹣1,0),(3,0),
可设交点式为y=a(x+1)(x﹣3),
把(0,﹣3)代入y=a(x+1)(x﹣3),
可得:﹣3=a(0+1)(0﹣3),
解得:a=1,
所以解析式为:y=x2﹣2x﹣3,
故选:B.
5.解:由图象可知抛物线开口向下,且与x轴的交点为(﹣1,0),(2,0),
∴抛物线的解析式为y=a(x+1)(x﹣2)=a(x2﹣x﹣2),
对比选项可知,选项A、B、C无法提取公因式后得到y=a(x2﹣x﹣2)的形式,而D选项中a=﹣1,
故选:D.
6.解:∵抛物线的顶点坐标为(﹣1,2020),
∴抛物线的解析式为y=a(x+1)2+2020,
∵抛物线y=a(x+1)2+2020与二次函数y=﹣5x2的图象相同,开口方向相同,
∴a=﹣5,
∴抛物线的解析式为y=﹣5(x+1)2+2020.
故选:D.
7.解:设抛物线解析式为y=a(x+1)(x﹣3),
把(0,3)代入得a 1 (﹣3)=3,解得a=﹣1,
所以抛物线解析式为y=﹣(x+1)(x﹣3),
即y=﹣x2+2x+3.
故选:A.
8.解:∵|m+3|+=0,
∴m=﹣3,n=2,即P(﹣3,2),
关于x轴对称点P′的坐标为(﹣3,﹣2),
则以P′为顶点的二次函数解析式为y=(x+3)2﹣2,
故选:B.
9.解:∵抛物线y=3(x﹣k﹣1)2+k2+2的顶点是(k+1,k2+2),
即当x=k+1时,y=k2+2,
∴k=x﹣1,
把k=x﹣1代入y=k2+2得y=(x﹣1)2+2=x2﹣2x+3,
所以(k,﹣3k2)在抛物线y=x2﹣2x+3上.
故选:C.
10.解:由图象知抛物线的对称轴为直线x=﹣1,
设抛物线解析式为y=a(x+1)2+k,
将(﹣3,0)、(0,3)代入,得:,
解得:,
则抛物线解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,
故选:D.
11.解:设二次函数的解析式为y=x2+bx+c,
把(0,﹣2)和(3,0)代入可得,
,
解得:,
∴题目中二次函数的表达式为:y=x﹣2,
故选:B.
12.解:∵抛物线y=﹣x2+bx+c,当1<x<3时,y值为正,当x<1或x>3时,y值为负.
∴抛物线与x轴的两交点坐标为(1,0)、(3,0),
∴y=﹣(x﹣1)(x﹣3),即y=﹣x2+4x﹣3,
故答案为y=﹣x2+4x﹣3.
13.解:图象顶点坐标为(2,3),
可以设函数解析式是y=a(x﹣2)2+3,
又∵形状与抛物线y=4x2相同,即二次项系数绝对值相同,
∴|a|=4,
∴这个函数解析式是:y=4(x﹣2)2+3或y=﹣4(x﹣2)2+3,
故答案为:y=4(x﹣2)2+3或y=﹣4(x﹣2)2+3.
14.解:过A作AD⊥y轴于D,过B作BE⊥y轴于E,如图:
∵AD⊥y轴,BE⊥y轴,
∴AD∥BE,
∴==,
∵CB=3AC,
∴CE=3CD,BE=3AD,
设AD=m,则BE=3m,
∵A、B两点在二次函数y=x2的图象上,
∴A(﹣m,m2),B(3m,9m2),
∴OD=m2,OE=9m2,
∴ED=8m2,
而CE=3CD,
∴CD=2m2,OC=3m2,
∴C(0,3m2),
∵P为CB的中点,
∴P(m,6m2),
又已知P(x,y),
∴,
∴y=x2;
故答案为:y=x2.
15.解:设抛物线的表达式为:y=ax2+bx+c,
则其对称轴为直线x=﹣=4,
∵顶点到x轴的距离为2,
额顶点坐标为(4,﹣2)或(4,2),
把顶点坐标代入抛物线解析式得:16a+4b+c=±2,
∵﹣=4,
即:2b+c=±2,
故满足这样条件的抛物线不唯一.
设a=2,当2b+c=2时,
则,
设a=2,当2b+c=﹣2时,
则,
故其中一个符合条件解析式为:y=﹣2x2﹣16x+34.
故答案为:y=﹣2x2﹣16x+34.答案不唯一.
16.解:设二次函数的解析式是y=ax2+bx+c,
∵经过原点,
∴c=0,
∵在y轴左侧的部分,图象上升,在y轴右侧的部分,图象下降,
∴a<0,﹣=0,
即:b=0,
只要满足a<0,b=0,c=0就行,如:a=﹣1,
所以二次函数的解析式是y=﹣x2.
故答案为:y=﹣x2.
17.解:在平行四边形ABCD中,CD∥AB且CD=AB=4,点D的坐标是(0,8),
∴点C的坐标为(4,8),
设抛物线的对称轴与x轴相交于点H,
则AH=BH=2,
∴点A,B的坐标为A(2,0),B(6,0),C(4,8),
设抛物线的解析式为y=a(x﹣4)2+8,
把A(2,0)代入得,0=4a+8,
解得a=﹣2,
∴y=﹣2(x﹣4)2+8,
∴抛物线的解析式为y=﹣2x2+16x﹣24,
故答案为y=﹣2x2+16x﹣24.
18.解:(1)把点A(1,0)和B(2,﹣1)代入y=ax2+bx+3中,
得:,
解得:,
∴抛物线的解析式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴该抛物线的顶点为(2,﹣1),
对称轴为直线x=2.
19.解:(1)根据题意得,
解得,.
∴二次函数的关系式为:y=﹣x2+2x+3,
∵y=﹣(x﹣1)2+4,
∴二次函数的顶点坐标(1,4).
(2)当y=3时,3=﹣(x﹣1)2+4,
解得,x1=0或x2=2,
∵y<3,
∴x<0或x>2.
20.解:(1)由点A的坐标知,OA=2,
∵OC=2OA=4,故点C的坐标为(0,4),
将点A、B、C的坐标代入抛物线表达式得:,
解得.
故抛物线的表达式为y=﹣x2+x+4;
将点B、C的坐标代入一次函数表达式得:,
解得,
故直线BC的表达式为y=﹣x+4;
(2)∵点A、B关于抛物线的对称轴对称,
设抛物线的对称轴交BC于点F,则点F为所求点,此时,当FA+FC的值最小,
由函数的对称性知,AF=BF,
则AF+FC=BF+FC=BC为最小,
当x=1时,y=﹣x+4=3,故点F(1,3),
由点B、C的坐标知,OB=OC=4,
则BC=BO=4,
即点F的坐标为(1,3)、FA+FC的最小值为4;
同步达标训练(附答案)
1.已知抛物线y=ax2+bx经过点A(﹣3,﹣3),且该抛物线的对称轴经过点A,则该抛物线的解析式为( )
A.y=﹣x2﹣2x B.y=﹣x2+2x C.y=x2﹣2x D.y=x2+2x
2.二次函数的图象如图所示,则这个二次函数的表达式为( )
A.y=x2+2x﹣3 B.y=x2﹣2x﹣3 C.y=﹣x2+2x﹣3 D.y=﹣x2﹣2x+3
3.如图,已知二次函数的图象,则它的表达式可能是( )
A.y=ax2+bx﹣(a﹣b) B.y=(x+a)(x﹣a+1)
C.y=(x﹣m)2+m2+1 D.y=x2+(a+2)x+a
4.如图是一条抛物线的图象,则其解析式为( )
A.y=x2﹣2x+3 B.y=x2﹣2x﹣3 C.y=x2+2x+3 D.y=x2+2x﹣3
5.抛物线的图象如图,根据图象可知,抛物线的解析式可能是( )
A.y=x2﹣x+2 B.y=﹣x2﹣x+2
C.y=﹣x2﹣x+1 D.y=﹣x2+x+2
6.已知抛物线与二次函数y=﹣5x2的图象相同,开口方向相同,且顶点坐标为(﹣1,2020),它对应的函数表达式为( )
A.y=﹣5(x﹣1) 2+2020 B.y=5(x﹣1) 2+2020
C.y=5(x+1) 2+2020 D.y=﹣5(x+1)2+2020
7.二次函数的图象如图所示,则其解析式是( )
A.y=﹣x2+2x+3 B.y=x2﹣2x﹣3 C.y=﹣x2﹣2x+3 D.y=﹣x2﹣2x﹣3
8.若|m+3|+=0,点P(m,n)关于x轴的对称点P′为二次函数图象顶点,则二次函数的解析式为( )
A.y=(x﹣3)2+2 B.y=(x+3)2﹣2
C.y=(x﹣3)2﹣2 D.y=(x+3)2+2
9.当k取任意实数时,抛物线y=3(x﹣k﹣1)2+k2+2的顶点所在的函数图象的解析式是( )
A.y=x2+2 B.y=x2﹣2x+1 C.y=x2﹣2x+3 D.y=x2+2x﹣3
10.二次函数部分图象如图所示,对称轴是直线x=﹣1,则这个二次函数的表达式为( )
A.y=﹣x2+2x+3 B.y=x2+2x+3 C.y=﹣x2+2x﹣3 D.y=﹣x2﹣2x+3
11.小聪做作业时不小心将墨水滴在一道数学题上,题目变为:“已知二次函数y=x2□x□的图象如图所示”,则题目中二次函数的表达式为( )
A.y=x2+x﹣2 B.y=x2﹣x﹣2 C.y=x2+x+2 D.y=x2﹣x+2
12.已知抛物线y=﹣x2+bx+c,当1<x<3时,y值为正,当x<1或x>3时,y值为负,则抛物线的解析式为 .
13.已知一个二次函数的图象形状与抛物线y=4x2相同,且顶点坐标为(2,3),则这个二次函数的解析式为 .
14.如图,在平面直角坐标系中,O为坐标原点,点C为y轴正半轴上的一个动点,过点C的直线与二次函数y=x2的图象交于A、B两点,且CB=3AC,P为CB的中点,设点P的坐标为P(x,y)(x>0),写出y关于x的函数表达式为: .
15.有一条抛物线,两位同学分别说了它的一个特点:
甲:对称轴是直线x=4;
乙:顶点到x轴的距离为2.
请你写出一个符合条件的解析式: .
16.已知一条抛物线具有以下特征:(1)经过原点;(2)在y轴左侧的部分,图象上升,在y轴右侧的部分,图象下降.试写出一个符合要求的抛物线的表达式: .
17.如图,平行四边形ABCD中,AB=4,点D的坐标是(0,8),以点C为顶点的抛物线经过x轴上的点A,B,则此抛物线的解析式为 .
18.在平面直角坐标系中,抛物线y=ax2+bx+3过点A(1,0)和B(2,﹣1).
(1)求二次函数的表达式;
(2)求二次函数图象的顶点坐标和对称轴.
19.如图,已知二次函数y=ax2+bx+c的图象过点A(﹣1,0)和点C(0,3),对称轴为直线x=1.
(1)求该二次函数的关系式和顶点坐标;
(2)结合图象,当y<3时,直接写出x的取值范围.
20.如图,抛物线y=ax2+bx+c经过点A(﹣2,0),B(4,0),与y轴正半轴交于点C,且OC=2OA,抛物线的顶点为D,对称轴交x轴于点E,直线y=mx+n经过B,C两点.
(1)求抛物线及直线BC的函数表达式;
(2)点F是抛物线对称轴上一点,当FA+FC的值最小时,求出点F的坐标及FA+FC的最小值.
参考答案
1.解:∵抛物线y=ax2+bx经过点A(﹣3,﹣3),且抛物线的对称轴经过点A,
∴函数的顶点坐标是(﹣3,﹣3),
∴,
解得,
∴该抛物线的解析式为y=.
故选:D.
2.解:从图象可知:二次函数的顶点坐标是(1,﹣4),与x轴的交点坐标是(﹣1,0),
设二次函数的解析式是y=a(x﹣1)2﹣4,
把(﹣1,0)代入得:0=a(﹣1﹣1)2﹣4,
解得:a=1,
所以y=(x﹣1)2﹣4=x2﹣2x﹣3,
故选:B.
3.解:A、y=ax2+bx﹣(a﹣b)=(ax﹣a+b)(x+1),令(ax﹣a+b)(x+1)=0得x1=,x2=﹣1,即图象与x轴一个交点横坐标应等于﹣1,故A不符合题意;
B、令y=0得x1=﹣a,x2=a﹣1,若﹣1<﹣a<0,则0<a<1,可得﹣1<a﹣1<0,同理若﹣1<a﹣1<0,则可得﹣1<﹣a<0,即抛物线与x轴两个交点横坐标都在﹣1到0之间,故B不符合题意;
C、抛物线y=(x﹣m)2+m2+1顶点为(m,m2+1),而m2+1>0,顶点在x轴上方,故C不符合题意;
D、图象可能为y=x2+(a+2)x+a,故D符合题意.
故选:D.
4.解:因为抛物线与x轴的交点坐标为(﹣1,0),(3,0),
可设交点式为y=a(x+1)(x﹣3),
把(0,﹣3)代入y=a(x+1)(x﹣3),
可得:﹣3=a(0+1)(0﹣3),
解得:a=1,
所以解析式为:y=x2﹣2x﹣3,
故选:B.
5.解:由图象可知抛物线开口向下,且与x轴的交点为(﹣1,0),(2,0),
∴抛物线的解析式为y=a(x+1)(x﹣2)=a(x2﹣x﹣2),
对比选项可知,选项A、B、C无法提取公因式后得到y=a(x2﹣x﹣2)的形式,而D选项中a=﹣1,
故选:D.
6.解:∵抛物线的顶点坐标为(﹣1,2020),
∴抛物线的解析式为y=a(x+1)2+2020,
∵抛物线y=a(x+1)2+2020与二次函数y=﹣5x2的图象相同,开口方向相同,
∴a=﹣5,
∴抛物线的解析式为y=﹣5(x+1)2+2020.
故选:D.
7.解:设抛物线解析式为y=a(x+1)(x﹣3),
把(0,3)代入得a 1 (﹣3)=3,解得a=﹣1,
所以抛物线解析式为y=﹣(x+1)(x﹣3),
即y=﹣x2+2x+3.
故选:A.
8.解:∵|m+3|+=0,
∴m=﹣3,n=2,即P(﹣3,2),
关于x轴对称点P′的坐标为(﹣3,﹣2),
则以P′为顶点的二次函数解析式为y=(x+3)2﹣2,
故选:B.
9.解:∵抛物线y=3(x﹣k﹣1)2+k2+2的顶点是(k+1,k2+2),
即当x=k+1时,y=k2+2,
∴k=x﹣1,
把k=x﹣1代入y=k2+2得y=(x﹣1)2+2=x2﹣2x+3,
所以(k,﹣3k2)在抛物线y=x2﹣2x+3上.
故选:C.
10.解:由图象知抛物线的对称轴为直线x=﹣1,
设抛物线解析式为y=a(x+1)2+k,
将(﹣3,0)、(0,3)代入,得:,
解得:,
则抛物线解析式为y=﹣(x+1)2+4=﹣x2﹣2x+3,
故选:D.
11.解:设二次函数的解析式为y=x2+bx+c,
把(0,﹣2)和(3,0)代入可得,
,
解得:,
∴题目中二次函数的表达式为:y=x﹣2,
故选:B.
12.解:∵抛物线y=﹣x2+bx+c,当1<x<3时,y值为正,当x<1或x>3时,y值为负.
∴抛物线与x轴的两交点坐标为(1,0)、(3,0),
∴y=﹣(x﹣1)(x﹣3),即y=﹣x2+4x﹣3,
故答案为y=﹣x2+4x﹣3.
13.解:图象顶点坐标为(2,3),
可以设函数解析式是y=a(x﹣2)2+3,
又∵形状与抛物线y=4x2相同,即二次项系数绝对值相同,
∴|a|=4,
∴这个函数解析式是:y=4(x﹣2)2+3或y=﹣4(x﹣2)2+3,
故答案为:y=4(x﹣2)2+3或y=﹣4(x﹣2)2+3.
14.解:过A作AD⊥y轴于D,过B作BE⊥y轴于E,如图:
∵AD⊥y轴,BE⊥y轴,
∴AD∥BE,
∴==,
∵CB=3AC,
∴CE=3CD,BE=3AD,
设AD=m,则BE=3m,
∵A、B两点在二次函数y=x2的图象上,
∴A(﹣m,m2),B(3m,9m2),
∴OD=m2,OE=9m2,
∴ED=8m2,
而CE=3CD,
∴CD=2m2,OC=3m2,
∴C(0,3m2),
∵P为CB的中点,
∴P(m,6m2),
又已知P(x,y),
∴,
∴y=x2;
故答案为:y=x2.
15.解:设抛物线的表达式为:y=ax2+bx+c,
则其对称轴为直线x=﹣=4,
∵顶点到x轴的距离为2,
额顶点坐标为(4,﹣2)或(4,2),
把顶点坐标代入抛物线解析式得:16a+4b+c=±2,
∵﹣=4,
即:2b+c=±2,
故满足这样条件的抛物线不唯一.
设a=2,当2b+c=2时,
则,
设a=2,当2b+c=﹣2时,
则,
故其中一个符合条件解析式为:y=﹣2x2﹣16x+34.
故答案为:y=﹣2x2﹣16x+34.答案不唯一.
16.解:设二次函数的解析式是y=ax2+bx+c,
∵经过原点,
∴c=0,
∵在y轴左侧的部分,图象上升,在y轴右侧的部分,图象下降,
∴a<0,﹣=0,
即:b=0,
只要满足a<0,b=0,c=0就行,如:a=﹣1,
所以二次函数的解析式是y=﹣x2.
故答案为:y=﹣x2.
17.解:在平行四边形ABCD中,CD∥AB且CD=AB=4,点D的坐标是(0,8),
∴点C的坐标为(4,8),
设抛物线的对称轴与x轴相交于点H,
则AH=BH=2,
∴点A,B的坐标为A(2,0),B(6,0),C(4,8),
设抛物线的解析式为y=a(x﹣4)2+8,
把A(2,0)代入得,0=4a+8,
解得a=﹣2,
∴y=﹣2(x﹣4)2+8,
∴抛物线的解析式为y=﹣2x2+16x﹣24,
故答案为y=﹣2x2+16x﹣24.
18.解:(1)把点A(1,0)和B(2,﹣1)代入y=ax2+bx+3中,
得:,
解得:,
∴抛物线的解析式为y=x2﹣4x+3;
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴该抛物线的顶点为(2,﹣1),
对称轴为直线x=2.
19.解:(1)根据题意得,
解得,.
∴二次函数的关系式为:y=﹣x2+2x+3,
∵y=﹣(x﹣1)2+4,
∴二次函数的顶点坐标(1,4).
(2)当y=3时,3=﹣(x﹣1)2+4,
解得,x1=0或x2=2,
∵y<3,
∴x<0或x>2.
20.解:(1)由点A的坐标知,OA=2,
∵OC=2OA=4,故点C的坐标为(0,4),
将点A、B、C的坐标代入抛物线表达式得:,
解得.
故抛物线的表达式为y=﹣x2+x+4;
将点B、C的坐标代入一次函数表达式得:,
解得,
故直线BC的表达式为y=﹣x+4;
(2)∵点A、B关于抛物线的对称轴对称,
设抛物线的对称轴交BC于点F,则点F为所求点,此时,当FA+FC的值最小,
由函数的对称性知,AF=BF,
则AF+FC=BF+FC=BC为最小,
当x=1时,y=﹣x+4=3,故点F(1,3),
由点B、C的坐标知,OB=OC=4,
则BC=BO=4,
即点F的坐标为(1,3)、FA+FC的最小值为4;
