2021-2022学年北师大版九年级数学下册2.4二次函数的应用 同步达标测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.4二次函数的应用 同步达标测评(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 442.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 09:21:32 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《2.4二次函数的应用》同步达标测评(附答案)
一.选择题(共8小题,满分32分)
1.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
2.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )
A.35元 B.36元 C.37元 D.36或37元
3.国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )
A.y=66(1﹣x) B.y=33(1﹣x) C.y=33(1﹣x2) D.y=33(1﹣x)2
4.某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式y=﹣5x+550,若要求销售单价不得低于成本,为了每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.90元,4500元 B.80元,4500元
C.90元,4000元 D.80元,4000元
5.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A.水流运行轨迹满足函数y=﹣x2﹣x+1
B.水流喷射的最远水平距离是40米
C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米
D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
6.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的面不能超过墙长,小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2.则:( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
7.如图,抛物线y=x+2交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A.n=(m﹣)2﹣ B.n=(m﹣)2
C.n=(m﹣)2﹣ D.n=(m﹣)2﹣
8.如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AE=6cm;
②当0<t≤10时,y=t2;
③直线NH的解析式为y=﹣5t+110;
④若△ABE与△QBP相似,则t=秒,
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共4小题,满分16分)
9.某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为 元时,网店该商品每天盈利最多.
10.去年下半年以来,我市遭遇连续干旱,各地河流的水位连续下降,小明仔细观察并测量自家门口的抛物线型拱桥的水位高度与水面宽度,发现两周以来每周水位下降的高度相同,而第一周水面宽度增加1米,而第二周水面宽度增加0.8米,小明刚开始观察时,他家门口抛物线型拱桥的水面宽为 米.
11.用一根长为20cm的铁丝围成一个矩形,该矩形面积的最大值是 cm2.
12.如图,某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=﹣,则隧道底部宽AB 米.
三.解答题(共8小题,满分72分)
13.某商场销售一种小商品,进货价为40元/件.当售价为60元/件时,每天的销售量为180件.在销售过程中发现:销售单价每上涨2元,每天的销售量就减少10件.设销售价格上涨x元/件(x为偶数),每天的销售量为y件.
(1)请写出y与x的函数关系式.
(2)商场要想每天销售该商品的利润为3900元,则每件涨价多少元?
(3)设商场每天销售该商品的利润为w元,则该商品的销售单价定为多少元时,每天获得的利润最大,最大利润是多少元?
14.某商家购进一批产品,成本为每件10元,采取线上和线下两种方式进行销售.调查发现:线下销售时,售价为12元可以销售1200件,每涨价1元则少售出100件.设线下的月销售量为y件,线下售价为每件x元(12≤x<24且x为整数).
(1)直接写出y与x的函数关系式;
(2)若线上每件售价始终比线下便宜2元,且线上的月销售量固定为400件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润;
(3)若月利润总和不低于6900元,则线下售价x的取值范围为 .
15.某校九年级一个数学综合实践小组去超市调查某种商品“十一”期间的销售情况,下面是调查后小阳与其他两位同学交流的情况:
小阳:据调查,该商品的进价为12元/件.
小佳:该商品定价为20元时,每天可售240件.
小欣:在定价为20元的基础上,每涨价1元,每天少售10件.
根据他们的对话,解决下列问题:
(1)若销售该商品每天能获利2470元,则该商品的定价应为多少?
(2)设每天销售该商品的利润为W元,且每件商品销售单价不高于26元,求该商品的销售单价定为多少元时,每天销售获得的利润最大,最大利润是多少?
16.某数学实验小组为学校制作了一个如图所示的三棱锥模型P﹣ABC,已知三条侧棱PA,PB,PC两两互相垂直,且棱PB与PC的和为6米,PB=2PA.现要给该模型的三个侧面(即Rt△PAB,Rt△PBC,Rt△PAC)刷上油漆,已知每平方米需要刷0.5升油漆,油漆的单价为60元/升.
(1)设PA的长为x米,三个侧面的面积之和为y平方米,试求y(平方米)关于x(米)的函数关系式;
(2)若油漆工的工时费为10元/平方米,该实验小组预算总费用为410元(即油漆费和工时费).试通过计算判断完成该模型的油漆工作是否会超出预算?
17.抛物线y=﹣x2+bx+c经过A(0,1)、B(4,3)两点,顶点为点P,连接PA,PB.
(1)求抛物线及直线AB的解析式;
(2)请你直接写出△PAB的面积;
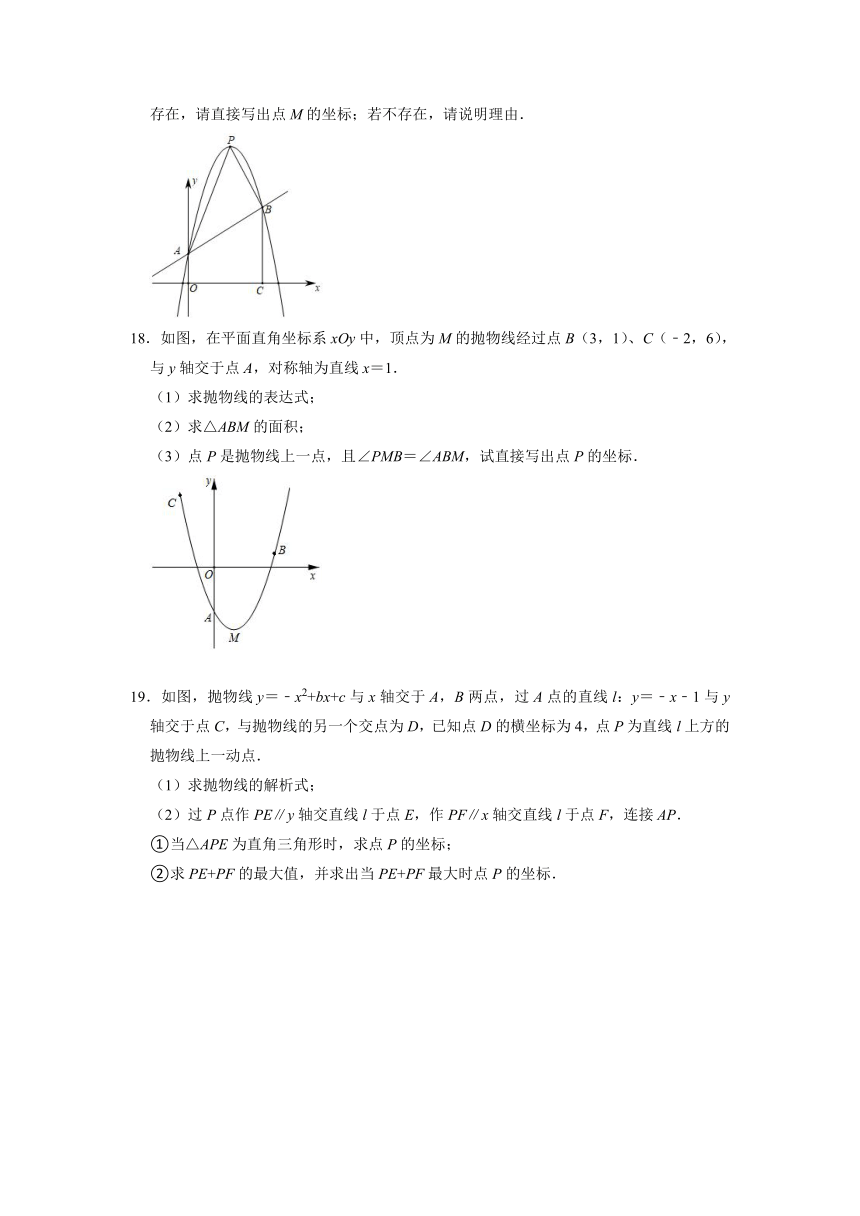
(3)过点B作BC⊥x轴,垂足为C,平行于y轴的直线交直线AB于点N,交抛物线于点M,是否存在点M,使以点B、点C、点M、点N为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系xOy中,顶点为M的抛物线经过点B(3,1)、C(﹣2,6),与y轴交于点A,对称轴为直线x=1.
(1)求抛物线的表达式;
(2)求△ABM的面积;
(3)点P是抛物线上一点,且∠PMB=∠ABM,试直接写出点P的坐标.
19.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,过A点的直线l:y=﹣x﹣1与y轴交于点C,与抛物线的另一个交点为D,已知点D的横坐标为4,点P为直线l上方的抛物线上一动点.
(1)求抛物线的解析式;
(2)过P点作PE∥y轴交直线l于点E,作PF∥x轴交直线l于点F,连接AP.
①当△APE为直角三角形时,求点P的坐标;
②求PE+PF的最大值,并求出当PE+PF最大时点P的坐标.
20.抛物线y=ax2+bx﹣2与x轴交于点A和B(﹣1,0),与y轴交于点C,直线y=﹣x+m过A,C两点,点P是抛物线上的一个动点.
(1)求抛物线的解析式;
(2)如图1,若点P在直线AC的上方,PE⊥AC于E,当PE=时,求点P的坐标;
(3)如图2,过B作y轴的平行线,点D在此直线上,且知点D的纵坐标为﹣3.连接AD,CD,当∠PAB与△ACD的一个内角相等时,请直接写出所有符合条件的点P的坐标.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵每涨价1元,每星期要少卖出5件,每件涨价x元,
∴销售每件的利润为(40﹣20+x)元,每星期的销售量为(200﹣5x)件,
∴每星期售出商品的利润y=(200﹣5x)(40﹣20+x).
故选:A.
2.解:设销售单价上涨x元,月销售利润为y元.
∵每件商品售价不能高于40元,
∴0≤x≤10,
依题意得:
y=(30﹣20+x)(240﹣10x)
=(10+x)(240﹣10x)
=﹣10x2+140x+2400
=﹣10(x﹣7)2+2890,
∴当x=7时,y最大=2890,
∴每件商品售价为30+7=37(元),
故选:C.
3.解:根据题意:平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,
可得y与x之间的函数关系为:y=33(1﹣x)2.
故选:D.
4.解:设每月总利润为w,依题意得w=y(x﹣50)=(﹣5x+550)(x﹣50)=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,
∵﹣5<0,此图象开口向下,
∴当x=80时,w有最大值为4500元,
∴为了每月所获利润最大,该商品销售单价应定为80元.
故选:B.
5.解:由题意可设抛物线的解析式为y=a(x﹣20)2+k,
将(0,1),(20,11)分别代入,得:,解得:,
∴y=﹣(x﹣20)2+11
=﹣x2+x+1,
故A错误;
∵坡度为1:10,
∴直线OA的解析式为y=0.1x,
当x=40时,y=0.1×40=4,
令y=4,得﹣x2+x+1=4,
∴x2﹣40x+120=0,
解得x=20±2≠40,
∴B错误;
设喷射出的水流与坡面OA之间的铅直高度为h米,
则h=﹣x2+x+1﹣0.1x=﹣x2+x+1,
∴对称轴为x=﹣=18,
∴hmax=9.1,故C正确;
将喷灌架向后移动7米,则图2中x=30时抛物线上的点的纵坐标值等于x=37时的函数值,
当x=37时,y=﹣×372+37+1=3.775,
在图2中,当x=30时,点B的纵坐标为:0.1×30+2.3=5.3,
则点A的纵坐标为5.3﹣2.3=3<3.775,故D错误.
故选:C.
6.解:设平行于墙的长度为xm(0<x≤5),隔离区的面积为Sm2,由题意得:
S=×x
=﹣x2+4x,
∴对称轴为x=﹣=6,
∵0<x≤5,抛物线开口向下,在对称轴左侧,S随x的增大而增大,
∴当x=5时,S有最大值:
Smax=﹣×52+4×5
=﹣+20
=.
∵9<<12,
∴小明错误;
令S=9得:9=﹣x2+4x,
解得:x1=9(舍),x2=3,
∴
x=3时,S=9.
∴隔离区的面积可能为9m2.
故选:B.
7.解:∵抛物线y=x+2交x轴于点A,B,交y轴于点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
∴BC的中点M坐标为(,),即点M坐标为(2,1).
∵点C沿着此抛物线运动,点M也随之运动,点M的运动轨迹是抛物线,且经过(2,1),(6,﹣1)
∴设抛物线的解析式为y=x2+bx+c,
则有,解得
∴m,n满足,n=m2﹣m+8=(m﹣)2﹣,
故选:D.
8.解:①观察图2可知:
当t=10时,点P、E重合,点Q、C重合;
当t=14时,点P、D重合.
∴BE=BC=10,DE=14﹣10=4,
∴AE=AD﹣DE=BC﹣DE=6,
∴①正确;
②设抛物线OM的函数解析式为y=ax2,
将点(10,40)代入y=ax2中,
得:40=100a,解得:a=,
∴当0<t≤10时,y=t2,②成立;
③在Rt△ABE中,∠BAE=90°,BE=10,AE=6,
∴AB==8,
∴点H的坐标为(14+8,0),即(22,0),
设直线NH的解析式为y=kt+b,
∴,解得:,
∴直线NH的解析式为y=﹣5t+110,③成立;
④当0<t≤10时,△QBP为等腰三角形,
△ABE为边长比为6:8:10的直角三角形,
∴当t=秒时,△ABE与△QBP不相似,④不正确.
综上可知:正确的结论有3个.
故选:C.
二.填空题(共4小题,满分16分)
9.解:设销售单价为x元,则每天可销售100﹣2(x﹣60)=(220﹣2x)件,每天盈利w元,
依题意得:w=(x﹣50)(220﹣2x)=﹣2x2+320x﹣11000=﹣2(x﹣80)2+1800,
∵﹣2<0,
∴当x=80时,w有最大值,最大值为1800元,
故答案为:80.
10.解:以第一天水面的中心与拱桥的中心为O点建立坐标系,
构建出如图模型:
其中OM=MN=1,CD﹣AB=1,EF﹣CD=0.8,
令OB=a,则MD=a+0.5,NF=a+0.9,
设抛物线方程为y=Ax2+B,
B(a,0),D(a+0.5,﹣1),F(a+0.9,﹣2)在抛物线上,
即,
即,
①﹣③得Aa+0.25A+1=0④,
②﹣③得1.8Aa+0.81A+2=0⑤,
⑤﹣④×2得﹣0.2Aa+0.31A=0,
即a=1.55,
则AB长为3.1米.
11.解:设矩形的长为xcm,则宽为(20÷2﹣x)cm,令矩形面积为ycm2,由题意得:
y=x(20÷2﹣x)
=x(10﹣x)
=﹣x2+10x
=﹣(x﹣5)2+25,
∴当x=5时,y有最大值为25,
∴该矩形面积的最大值是25cm2.
故答案为:25.
12.解:∵y=﹣,最大高度为8米,
∴b=8,
∴抛物线解析式为y=﹣x2+8,
当y=0时,则0=﹣x2+8,
解得:x=4或﹣4,
∴水面宽AB是4+4=8米.
故答案为:8.
三.解答题(共8小题,满分72分)
13.解:(1)由题意得:y=180﹣×10=﹣5x+180,
∴y与x的函数关系式为y=﹣5x+180;
(2)由题意得:(60+x﹣40)(﹣5x+180)=3900,
整理得:x2﹣16x+60=0,
解得:x1=6,x2=10,
∴商场要想每天销售该商品的利润为3900元,则每件涨价6元或10元;
(3)由题意得:w=(60+x﹣40)(﹣5x+180)
=﹣5x2+80x+3600
=﹣5(x﹣8)2+3920,
∵﹣5<0,
∴当x=8时,w最大,最大值为3920,
∴每件涨价8元,销售价定为68元时,每天获得的利润最大,最大利润是3620元.
14.解:(1)由题意,得:y=1200﹣100(x﹣12)=﹣100x+2400,
∴y与x的函数关系式为y=﹣100x+2400(12≤x<24且x为整数);
(2)设总利润为w元,
w=(x﹣10)(﹣100x+2400)+(x﹣2﹣10)×400=﹣100(x﹣19)2+7300,
∵﹣100<0,12≤x<24,
∴当x=19时,w取得最大值,此时w=7300,
答:当x为19时,线上和线下月利润总和达到最大,此时的最大利润是7300元;
(3)由(2)知,w=﹣100(x﹣19)2+7300,
令w=6900,则﹣100(x﹣19)2+7300=6900,
解得:x1=17,x2=21,
根据二次函数的图象和性质,
当17≤x≤21时,w≥6900,
∴当17≤x≤21时,月利润总和不低于6900元,
故答案为:17≤x≤21.
15.解:(1)设每件商品定价为x元,则每件商品的销售利润为(x﹣12)元,
根据题意得:(x﹣12)[240﹣10(x﹣20)]=2470,
整理得:x2﹣56x+775=0,
解得x1=25,x2=31,
∴该商品的定价应为22元或24元;
(2)设每件商品定价为x元,由题意得:
W=(x﹣12)[240﹣10(x﹣20)]=﹣10x2+560x﹣5280=﹣10(x﹣28)2+2560,
∵﹣10<0,
∴当x<28时,W随x的增大而增大,
∵每件商品销售单价不高于26元,
∴x≤26,
∴当x=26时,W最大,最大值为2520,
∴该商品的销售单价定为26元时,每天销售获得的利润最大,最大利润是2520元.
16.解:(1)∵PA=x米,PB=2PA,PB+PC=6米,
∴PB=2x米,PC=(6﹣2x)米,
由题意,得:y=PA PB+PA PC+PB PC
=x 2x+x(6﹣2x)+×2x(6﹣2x)
=x2+3x﹣x2+6x﹣2x2
=﹣2x2+9x,
∴y关于x的函数关系式为y=﹣2x2+9x;
(2)由(1)知,y=﹣2x2+9x=﹣2(x﹣)2+,
∵﹣2<0,
∴当x=时,y有最大值,最大值,
当y取得最大值时,需要总费用为:×(0.5×60+10)=405(元),
∵405<410,
∴完成该模型的油漆工作不否会超出预算.
17.解:(1)∵抛物线y=﹣x2+bx+c经过A(0,1),B(4,3)两点,
∴,
解得,
即该抛物线的解析式为y=﹣x2+x+1,
设直线AB的解析式为y=kx+m,
∴,
解得,
∴直线AB的解析式为y=x+1;
(2)如图,过点P作PD∥y轴,交AB于点D,
∵y=﹣x2+x+1=,
∴顶点P的坐标为(,),
∵直线AB的解析式为y=x+1,
当x=时,y=+1=,
∴D(,),
∴PD==,
∴S△PAB=×4=;
(3)设M(n,﹣n2+n+1),N(n,n+1),
∴MN=|﹣n2+n﹣1|=|﹣n2+4n|,
∵以点B、点C、点M、点N为顶点的四边形为平行四边形,BC∥MN,
∴MN=BC=3,
∴|﹣n2+4n|=3,
∴﹣n2+4n=3或n2﹣4n=3,
当﹣n2+4n=3时,
n1=1,n2=3,
∴M(1,)或(3,),
当n2﹣4n=3时,
n1=2+,n2=2﹣,
∴M(2+,﹣1+)或(2﹣,﹣1﹣),
综合以上可得,点M的坐标为(1,)或(3,)或(2+,﹣1+)或(2﹣,﹣1﹣).
18.解:(1)设抛物线解析式为y=ax2+bx+c,
∵抛物线经过点B(3,1)、C(﹣2,6),对称轴为直线x=1,
∴,
解得:,
∴设抛物线解析式为:y=x2﹣2x﹣2;
(2)如图1,连接AB,过点M作y轴的平行线交AB于点Q,连接AM、BM,
当x=0时,y=﹣2,当x=1时,y=﹣3,
∴A(0,﹣2),M(1,﹣3),
设直线AB的解析式为y=mx+n,
把A(0,﹣2),B(3,1)代入得:
,
解得:,
∴y=x﹣2,
当x=1时,y=﹣1,
∴Q(1,﹣1),
∴MQ=﹣1﹣(﹣3)=2,
∴S△ABM=S△MQA+S△MQB
= MQ |xB﹣xA|
=×2×|3﹣0|
=3;
(3)如图2,分两种情况分类讨论:
①当PM在AB的左侧时,PM交AB于点D,设D(t,t﹣2),
∵B(3,1)、M(1,﹣3),
∴BD=,MD=,
∵∠PMB=∠ABM,
∴BD=MD,
∴=,
解得:t=,
∴D(,﹣),
设直线MD的解析式为y=kx+b,
∴,
解得:,
∴直线MD的解析式为y=7x﹣10,
∴,
解得:,,
∴P(8,46),
②当PM在AB的右侧时,PM交抛物线于点P,
∵∠PMB=∠ABM,
∴AB∥PM,
∴设直线MP的解析式为y=x+d,
把M(1,﹣3)代入得:﹣3=1+d,
∴d=﹣4,
∴直线MP的解析式为y=x﹣4,
∴,
解得:,,
∴P(2,﹣2),
综上所述,点P的坐标为(8,46)或(2,﹣2).
19.解:(1)令y=0,则x=﹣1,
∴A(﹣1,0),
当x=4时,y=﹣5,
∴D(4,﹣5),
∴,
∴,
∴y=﹣x2+2x+3;
(2)设P(m,﹣m2+2m+3),
当x=0时,y=﹣1,
∴C(0,﹣1),
∴OA=OC=1,
∵∠AOC=90°,
∴∠OAC=∠OCA=45°,
①当PE∥y轴时,
∴∠PEA=∠OCA=45°,
∴当△APE为直角三角形时,∠PAE=90°或∠APE=90°,
当∠PAE=90°时,∠PAB=∠PAE﹣∠OAC=45°,
设PE与x轴交于点M,则∠PAM=∠APM=45°,
∴AM=PM,即﹣m2+2m+3=m+1,
解得m=2或m=﹣1(舍),
∴P(2,3);
当∠APE=90°时,点P与点B重合,
∴﹣m2+2m+3=0,
解得m=3或m=﹣1(舍),
∴P(3,0);
综上所述:P点坐标为(3,0)或(2,3);
②∵PF∥x轴,
∴∠PFE=∠OAC=45°,
∴∠PFE=∠PEF,
∴PE=PF,
∴PE+PF=2PE=2(﹣m2+2m+3+m+1)=﹣2(m﹣)2+,
∴当m=时,PE+PF取最大值,
此时P(,).
20.解:(1)令x=0,则y=﹣2,
∴C(0,﹣2),
∵直线y=﹣x+m过C点,
∴m=﹣2,
∴y=﹣x﹣2,
取y=0,得x=﹣4,
∴A(﹣4,0),
将点A(﹣4,0)和B(﹣1,0)代入y=ax2+bx﹣2,
得,
∴,
∴y=﹣x2﹣x﹣2;
(2)如图1,过点E作EF⊥x轴,过点P作PF⊥y轴,交EF于点F,过点C作CG⊥y轴,交EF于点G,
∵PE⊥EC,
∴∠FEP+∠GEC=90°,
∵∠FEP+∠FPE=90°,
∴∠FPE=∠GEC,
∴∠DCG=∠FEP,
∵CG∥x轴,
∴∠ECG=∠OAC,
∵OA=4,OB=2,
∴tan∠OAC=,
∴=,
∵PE=,
∴PF=,EF=,
设P(t,﹣t2﹣t﹣2),
∴E(t﹣,﹣t2﹣t﹣2﹣),
∴﹣t2﹣t﹣2﹣=﹣×(t﹣)﹣2,
解得t=﹣1或t=﹣3,
∴P(﹣1,0)或P(﹣3,1);
(3)如图2,过点P作PH⊥x轴交于点H,
∵D点横坐标为﹣3,
∴D(﹣1,﹣3),
∴AD=3,AC=2,CD=,
∵AD2=AC2+CD2,
∴△ACD是直角三角形,
∴AD⊥CD,
∴tan∠CAD==,
设P(m,﹣m2﹣m﹣2),
∴PH=|﹣m2﹣m﹣2|,AH=|m+4|,
当∠PAH=∠CAD时,=,
∴3×|﹣m2﹣m﹣2|=|m+4|,
解得m=﹣或m=﹣,
∴P(﹣,)或P(﹣,﹣);
当∠APH=∠CAD时,=3,
∴|﹣m2﹣m﹣2|=3×|m+4|,
解得m=﹣7或m=5,
当m=﹣7时,∠PAB为钝角,
∴m=﹣7时不合题意,
∴P(5,﹣27)或P(﹣7,﹣9);
综上所述:P点的坐标为(﹣,)或(﹣,﹣)或(5,﹣27).
一.选择题(共8小题,满分32分)
1.某商品的进价为每件20元,现在的售价为每件40元,每星期可卖出200件.市场调查反映:如调整价格,每涨价1元,每星期要少卖出5件.则每星期售出商品的利润y(单位:元)与每件涨价x(单位:元)之间的函数关系式是( )
A.y=(200﹣5x)(40﹣20+x) B.y=(200+5x)(40﹣20﹣x)
C.y=200(40﹣20﹣x) D.y=200﹣5x
2.某商场经营一种小商品,已知进购时单价是20元.调查发现:当销售单价是30元时,月销售量为240件,而销售单价每上涨1元,月销售量就减少10件,但每件商品的售价不能高于40元.当月销售利润最大时,销售单价为( )
A.35元 B.36元 C.37元 D.36或37元
3.国家决定对某药品分两次降价,若设平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,则y与x之间的函数关系为( )
A.y=66(1﹣x) B.y=33(1﹣x) C.y=33(1﹣x2) D.y=33(1﹣x)2
4.某超市销售一种商品,每件成本为50元,销售人员经调查发现,该商品每月的销售量y(件)与销售单价x(元)之间满足函数关系式y=﹣5x+550,若要求销售单价不得低于成本,为了每月所获利润最大,该商品销售单价应定为多少元?每月最大利润是多少?( )
A.90元,4500元 B.80元,4500元
C.90元,4000元 D.80元,4000元
5.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A.水流运行轨迹满足函数y=﹣x2﹣x+1
B.水流喷射的最远水平距离是40米
C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米
D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
6.如图,预防新冠肺炎疫情期间,某校在校门口用塑料膜围成一个临时隔离区,隔离区一面靠长为5m的墙,隔离区分成两个区域,中间用塑料膜隔开.已知整个隔离区塑料膜总长为12m,如果隔离区出入口的大小不计,并且隔离区靠墙的面不能超过墙长,小明认为:隔离区的最大面积为12m2;小亮认为:隔离区的面积可能为9m2.则:( )
A.小明正确,小亮错误 B.小明错误,小亮正确
C.两人均正确 D.两人均错误
7.如图,抛物线y=x+2交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A.n=(m﹣)2﹣ B.n=(m﹣)2
C.n=(m﹣)2﹣ D.n=(m﹣)2﹣
8.如图1,点E为矩形ABCD边AD上一点,点P点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s.设P,Q出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分).则下列结论:
①AE=6cm;
②当0<t≤10时,y=t2;
③直线NH的解析式为y=﹣5t+110;
④若△ABE与△QBP相似,则t=秒,
其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共4小题,满分16分)
9.某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为 元时,网店该商品每天盈利最多.
10.去年下半年以来,我市遭遇连续干旱,各地河流的水位连续下降,小明仔细观察并测量自家门口的抛物线型拱桥的水位高度与水面宽度,发现两周以来每周水位下降的高度相同,而第一周水面宽度增加1米,而第二周水面宽度增加0.8米,小明刚开始观察时,他家门口抛物线型拱桥的水面宽为 米.
11.用一根长为20cm的铁丝围成一个矩形,该矩形面积的最大值是 cm2.
12.如图,某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=﹣,则隧道底部宽AB 米.
三.解答题(共8小题,满分72分)
13.某商场销售一种小商品,进货价为40元/件.当售价为60元/件时,每天的销售量为180件.在销售过程中发现:销售单价每上涨2元,每天的销售量就减少10件.设销售价格上涨x元/件(x为偶数),每天的销售量为y件.
(1)请写出y与x的函数关系式.
(2)商场要想每天销售该商品的利润为3900元,则每件涨价多少元?
(3)设商场每天销售该商品的利润为w元,则该商品的销售单价定为多少元时,每天获得的利润最大,最大利润是多少元?
14.某商家购进一批产品,成本为每件10元,采取线上和线下两种方式进行销售.调查发现:线下销售时,售价为12元可以销售1200件,每涨价1元则少售出100件.设线下的月销售量为y件,线下售价为每件x元(12≤x<24且x为整数).
(1)直接写出y与x的函数关系式;
(2)若线上每件售价始终比线下便宜2元,且线上的月销售量固定为400件.试问:当x为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润;
(3)若月利润总和不低于6900元,则线下售价x的取值范围为 .
15.某校九年级一个数学综合实践小组去超市调查某种商品“十一”期间的销售情况,下面是调查后小阳与其他两位同学交流的情况:
小阳:据调查,该商品的进价为12元/件.
小佳:该商品定价为20元时,每天可售240件.
小欣:在定价为20元的基础上,每涨价1元,每天少售10件.
根据他们的对话,解决下列问题:
(1)若销售该商品每天能获利2470元,则该商品的定价应为多少?
(2)设每天销售该商品的利润为W元,且每件商品销售单价不高于26元,求该商品的销售单价定为多少元时,每天销售获得的利润最大,最大利润是多少?
16.某数学实验小组为学校制作了一个如图所示的三棱锥模型P﹣ABC,已知三条侧棱PA,PB,PC两两互相垂直,且棱PB与PC的和为6米,PB=2PA.现要给该模型的三个侧面(即Rt△PAB,Rt△PBC,Rt△PAC)刷上油漆,已知每平方米需要刷0.5升油漆,油漆的单价为60元/升.
(1)设PA的长为x米,三个侧面的面积之和为y平方米,试求y(平方米)关于x(米)的函数关系式;
(2)若油漆工的工时费为10元/平方米,该实验小组预算总费用为410元(即油漆费和工时费).试通过计算判断完成该模型的油漆工作是否会超出预算?
17.抛物线y=﹣x2+bx+c经过A(0,1)、B(4,3)两点,顶点为点P,连接PA,PB.
(1)求抛物线及直线AB的解析式;
(2)请你直接写出△PAB的面积;
(3)过点B作BC⊥x轴,垂足为C,平行于y轴的直线交直线AB于点N,交抛物线于点M,是否存在点M,使以点B、点C、点M、点N为顶点的四边形为平行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系xOy中,顶点为M的抛物线经过点B(3,1)、C(﹣2,6),与y轴交于点A,对称轴为直线x=1.
(1)求抛物线的表达式;
(2)求△ABM的面积;
(3)点P是抛物线上一点,且∠PMB=∠ABM,试直接写出点P的坐标.
19.如图,抛物线y=﹣x2+bx+c与x轴交于A,B两点,过A点的直线l:y=﹣x﹣1与y轴交于点C,与抛物线的另一个交点为D,已知点D的横坐标为4,点P为直线l上方的抛物线上一动点.
(1)求抛物线的解析式;
(2)过P点作PE∥y轴交直线l于点E,作PF∥x轴交直线l于点F,连接AP.
①当△APE为直角三角形时,求点P的坐标;
②求PE+PF的最大值,并求出当PE+PF最大时点P的坐标.
20.抛物线y=ax2+bx﹣2与x轴交于点A和B(﹣1,0),与y轴交于点C,直线y=﹣x+m过A,C两点,点P是抛物线上的一个动点.
(1)求抛物线的解析式;
(2)如图1,若点P在直线AC的上方,PE⊥AC于E,当PE=时,求点P的坐标;
(3)如图2,过B作y轴的平行线,点D在此直线上,且知点D的纵坐标为﹣3.连接AD,CD,当∠PAB与△ACD的一个内角相等时,请直接写出所有符合条件的点P的坐标.
参考答案
一.选择题(共8小题,满分32分)
1.解:∵每涨价1元,每星期要少卖出5件,每件涨价x元,
∴销售每件的利润为(40﹣20+x)元,每星期的销售量为(200﹣5x)件,
∴每星期售出商品的利润y=(200﹣5x)(40﹣20+x).
故选:A.
2.解:设销售单价上涨x元,月销售利润为y元.
∵每件商品售价不能高于40元,
∴0≤x≤10,
依题意得:
y=(30﹣20+x)(240﹣10x)
=(10+x)(240﹣10x)
=﹣10x2+140x+2400
=﹣10(x﹣7)2+2890,
∴当x=7时,y最大=2890,
∴每件商品售价为30+7=37(元),
故选:C.
3.解:根据题意:平均每次降价的百分比为x,该药品的原价为33元,降价后的价格为y元,
可得y与x之间的函数关系为:y=33(1﹣x)2.
故选:D.
4.解:设每月总利润为w,依题意得w=y(x﹣50)=(﹣5x+550)(x﹣50)=﹣5x2+800x﹣27500=﹣5(x﹣80)2+4500,
∵﹣5<0,此图象开口向下,
∴当x=80时,w有最大值为4500元,
∴为了每月所获利润最大,该商品销售单价应定为80元.
故选:B.
5.解:由题意可设抛物线的解析式为y=a(x﹣20)2+k,
将(0,1),(20,11)分别代入,得:,解得:,
∴y=﹣(x﹣20)2+11
=﹣x2+x+1,
故A错误;
∵坡度为1:10,
∴直线OA的解析式为y=0.1x,
当x=40时,y=0.1×40=4,
令y=4,得﹣x2+x+1=4,
∴x2﹣40x+120=0,
解得x=20±2≠40,
∴B错误;
设喷射出的水流与坡面OA之间的铅直高度为h米,
则h=﹣x2+x+1﹣0.1x=﹣x2+x+1,
∴对称轴为x=﹣=18,
∴hmax=9.1,故C正确;
将喷灌架向后移动7米,则图2中x=30时抛物线上的点的纵坐标值等于x=37时的函数值,
当x=37时,y=﹣×372+37+1=3.775,
在图2中,当x=30时,点B的纵坐标为:0.1×30+2.3=5.3,
则点A的纵坐标为5.3﹣2.3=3<3.775,故D错误.
故选:C.
6.解:设平行于墙的长度为xm(0<x≤5),隔离区的面积为Sm2,由题意得:
S=×x
=﹣x2+4x,
∴对称轴为x=﹣=6,
∵0<x≤5,抛物线开口向下,在对称轴左侧,S随x的增大而增大,
∴当x=5时,S有最大值:
Smax=﹣×52+4×5
=﹣+20
=.
∵9<<12,
∴小明错误;
令S=9得:9=﹣x2+4x,
解得:x1=9(舍),x2=3,
∴
x=3时,S=9.
∴隔离区的面积可能为9m2.
故选:B.
7.解:∵抛物线y=x+2交x轴于点A,B,交y轴于点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
∴BC的中点M坐标为(,),即点M坐标为(2,1).
∵点C沿着此抛物线运动,点M也随之运动,点M的运动轨迹是抛物线,且经过(2,1),(6,﹣1)
∴设抛物线的解析式为y=x2+bx+c,
则有,解得
∴m,n满足,n=m2﹣m+8=(m﹣)2﹣,
故选:D.
8.解:①观察图2可知:
当t=10时,点P、E重合,点Q、C重合;
当t=14时,点P、D重合.
∴BE=BC=10,DE=14﹣10=4,
∴AE=AD﹣DE=BC﹣DE=6,
∴①正确;
②设抛物线OM的函数解析式为y=ax2,
将点(10,40)代入y=ax2中,
得:40=100a,解得:a=,
∴当0<t≤10时,y=t2,②成立;
③在Rt△ABE中,∠BAE=90°,BE=10,AE=6,
∴AB==8,
∴点H的坐标为(14+8,0),即(22,0),
设直线NH的解析式为y=kt+b,
∴,解得:,
∴直线NH的解析式为y=﹣5t+110,③成立;
④当0<t≤10时,△QBP为等腰三角形,
△ABE为边长比为6:8:10的直角三角形,
∴当t=秒时,△ABE与△QBP不相似,④不正确.
综上可知:正确的结论有3个.
故选:C.
二.填空题(共4小题,满分16分)
9.解:设销售单价为x元,则每天可销售100﹣2(x﹣60)=(220﹣2x)件,每天盈利w元,
依题意得:w=(x﹣50)(220﹣2x)=﹣2x2+320x﹣11000=﹣2(x﹣80)2+1800,
∵﹣2<0,
∴当x=80时,w有最大值,最大值为1800元,
故答案为:80.
10.解:以第一天水面的中心与拱桥的中心为O点建立坐标系,
构建出如图模型:
其中OM=MN=1,CD﹣AB=1,EF﹣CD=0.8,
令OB=a,则MD=a+0.5,NF=a+0.9,
设抛物线方程为y=Ax2+B,
B(a,0),D(a+0.5,﹣1),F(a+0.9,﹣2)在抛物线上,
即,
即,
①﹣③得Aa+0.25A+1=0④,
②﹣③得1.8Aa+0.81A+2=0⑤,
⑤﹣④×2得﹣0.2Aa+0.31A=0,
即a=1.55,
则AB长为3.1米.
11.解:设矩形的长为xcm,则宽为(20÷2﹣x)cm,令矩形面积为ycm2,由题意得:
y=x(20÷2﹣x)
=x(10﹣x)
=﹣x2+10x
=﹣(x﹣5)2+25,
∴当x=5时,y有最大值为25,
∴该矩形面积的最大值是25cm2.
故答案为:25.
12.解:∵y=﹣,最大高度为8米,
∴b=8,
∴抛物线解析式为y=﹣x2+8,
当y=0时,则0=﹣x2+8,
解得:x=4或﹣4,
∴水面宽AB是4+4=8米.
故答案为:8.
三.解答题(共8小题,满分72分)
13.解:(1)由题意得:y=180﹣×10=﹣5x+180,
∴y与x的函数关系式为y=﹣5x+180;
(2)由题意得:(60+x﹣40)(﹣5x+180)=3900,
整理得:x2﹣16x+60=0,
解得:x1=6,x2=10,
∴商场要想每天销售该商品的利润为3900元,则每件涨价6元或10元;
(3)由题意得:w=(60+x﹣40)(﹣5x+180)
=﹣5x2+80x+3600
=﹣5(x﹣8)2+3920,
∵﹣5<0,
∴当x=8时,w最大,最大值为3920,
∴每件涨价8元,销售价定为68元时,每天获得的利润最大,最大利润是3620元.
14.解:(1)由题意,得:y=1200﹣100(x﹣12)=﹣100x+2400,
∴y与x的函数关系式为y=﹣100x+2400(12≤x<24且x为整数);
(2)设总利润为w元,
w=(x﹣10)(﹣100x+2400)+(x﹣2﹣10)×400=﹣100(x﹣19)2+7300,
∵﹣100<0,12≤x<24,
∴当x=19时,w取得最大值,此时w=7300,
答:当x为19时,线上和线下月利润总和达到最大,此时的最大利润是7300元;
(3)由(2)知,w=﹣100(x﹣19)2+7300,
令w=6900,则﹣100(x﹣19)2+7300=6900,
解得:x1=17,x2=21,
根据二次函数的图象和性质,
当17≤x≤21时,w≥6900,
∴当17≤x≤21时,月利润总和不低于6900元,
故答案为:17≤x≤21.
15.解:(1)设每件商品定价为x元,则每件商品的销售利润为(x﹣12)元,
根据题意得:(x﹣12)[240﹣10(x﹣20)]=2470,
整理得:x2﹣56x+775=0,
解得x1=25,x2=31,
∴该商品的定价应为22元或24元;
(2)设每件商品定价为x元,由题意得:
W=(x﹣12)[240﹣10(x﹣20)]=﹣10x2+560x﹣5280=﹣10(x﹣28)2+2560,
∵﹣10<0,
∴当x<28时,W随x的增大而增大,
∵每件商品销售单价不高于26元,
∴x≤26,
∴当x=26时,W最大,最大值为2520,
∴该商品的销售单价定为26元时,每天销售获得的利润最大,最大利润是2520元.
16.解:(1)∵PA=x米,PB=2PA,PB+PC=6米,
∴PB=2x米,PC=(6﹣2x)米,
由题意,得:y=PA PB+PA PC+PB PC
=x 2x+x(6﹣2x)+×2x(6﹣2x)
=x2+3x﹣x2+6x﹣2x2
=﹣2x2+9x,
∴y关于x的函数关系式为y=﹣2x2+9x;
(2)由(1)知,y=﹣2x2+9x=﹣2(x﹣)2+,
∵﹣2<0,
∴当x=时,y有最大值,最大值,
当y取得最大值时,需要总费用为:×(0.5×60+10)=405(元),
∵405<410,
∴完成该模型的油漆工作不否会超出预算.
17.解:(1)∵抛物线y=﹣x2+bx+c经过A(0,1),B(4,3)两点,
∴,
解得,
即该抛物线的解析式为y=﹣x2+x+1,
设直线AB的解析式为y=kx+m,
∴,
解得,
∴直线AB的解析式为y=x+1;
(2)如图,过点P作PD∥y轴,交AB于点D,
∵y=﹣x2+x+1=,
∴顶点P的坐标为(,),
∵直线AB的解析式为y=x+1,
当x=时,y=+1=,
∴D(,),
∴PD==,
∴S△PAB=×4=;
(3)设M(n,﹣n2+n+1),N(n,n+1),
∴MN=|﹣n2+n﹣1|=|﹣n2+4n|,
∵以点B、点C、点M、点N为顶点的四边形为平行四边形,BC∥MN,
∴MN=BC=3,
∴|﹣n2+4n|=3,
∴﹣n2+4n=3或n2﹣4n=3,
当﹣n2+4n=3时,
n1=1,n2=3,
∴M(1,)或(3,),
当n2﹣4n=3时,
n1=2+,n2=2﹣,
∴M(2+,﹣1+)或(2﹣,﹣1﹣),
综合以上可得,点M的坐标为(1,)或(3,)或(2+,﹣1+)或(2﹣,﹣1﹣).
18.解:(1)设抛物线解析式为y=ax2+bx+c,
∵抛物线经过点B(3,1)、C(﹣2,6),对称轴为直线x=1,
∴,
解得:,
∴设抛物线解析式为:y=x2﹣2x﹣2;
(2)如图1,连接AB,过点M作y轴的平行线交AB于点Q,连接AM、BM,
当x=0时,y=﹣2,当x=1时,y=﹣3,
∴A(0,﹣2),M(1,﹣3),
设直线AB的解析式为y=mx+n,
把A(0,﹣2),B(3,1)代入得:
,
解得:,
∴y=x﹣2,
当x=1时,y=﹣1,
∴Q(1,﹣1),
∴MQ=﹣1﹣(﹣3)=2,
∴S△ABM=S△MQA+S△MQB
= MQ |xB﹣xA|
=×2×|3﹣0|
=3;
(3)如图2,分两种情况分类讨论:
①当PM在AB的左侧时,PM交AB于点D,设D(t,t﹣2),
∵B(3,1)、M(1,﹣3),
∴BD=,MD=,
∵∠PMB=∠ABM,
∴BD=MD,
∴=,
解得:t=,
∴D(,﹣),
设直线MD的解析式为y=kx+b,
∴,
解得:,
∴直线MD的解析式为y=7x﹣10,
∴,
解得:,,
∴P(8,46),
②当PM在AB的右侧时,PM交抛物线于点P,
∵∠PMB=∠ABM,
∴AB∥PM,
∴设直线MP的解析式为y=x+d,
把M(1,﹣3)代入得:﹣3=1+d,
∴d=﹣4,
∴直线MP的解析式为y=x﹣4,
∴,
解得:,,
∴P(2,﹣2),
综上所述,点P的坐标为(8,46)或(2,﹣2).
19.解:(1)令y=0,则x=﹣1,
∴A(﹣1,0),
当x=4时,y=﹣5,
∴D(4,﹣5),
∴,
∴,
∴y=﹣x2+2x+3;
(2)设P(m,﹣m2+2m+3),
当x=0时,y=﹣1,
∴C(0,﹣1),
∴OA=OC=1,
∵∠AOC=90°,
∴∠OAC=∠OCA=45°,
①当PE∥y轴时,
∴∠PEA=∠OCA=45°,
∴当△APE为直角三角形时,∠PAE=90°或∠APE=90°,
当∠PAE=90°时,∠PAB=∠PAE﹣∠OAC=45°,
设PE与x轴交于点M,则∠PAM=∠APM=45°,
∴AM=PM,即﹣m2+2m+3=m+1,
解得m=2或m=﹣1(舍),
∴P(2,3);
当∠APE=90°时,点P与点B重合,
∴﹣m2+2m+3=0,
解得m=3或m=﹣1(舍),
∴P(3,0);
综上所述:P点坐标为(3,0)或(2,3);
②∵PF∥x轴,
∴∠PFE=∠OAC=45°,
∴∠PFE=∠PEF,
∴PE=PF,
∴PE+PF=2PE=2(﹣m2+2m+3+m+1)=﹣2(m﹣)2+,
∴当m=时,PE+PF取最大值,
此时P(,).
20.解:(1)令x=0,则y=﹣2,
∴C(0,﹣2),
∵直线y=﹣x+m过C点,
∴m=﹣2,
∴y=﹣x﹣2,
取y=0,得x=﹣4,
∴A(﹣4,0),
将点A(﹣4,0)和B(﹣1,0)代入y=ax2+bx﹣2,
得,
∴,
∴y=﹣x2﹣x﹣2;
(2)如图1,过点E作EF⊥x轴,过点P作PF⊥y轴,交EF于点F,过点C作CG⊥y轴,交EF于点G,
∵PE⊥EC,
∴∠FEP+∠GEC=90°,
∵∠FEP+∠FPE=90°,
∴∠FPE=∠GEC,
∴∠DCG=∠FEP,
∵CG∥x轴,
∴∠ECG=∠OAC,
∵OA=4,OB=2,
∴tan∠OAC=,
∴=,
∵PE=,
∴PF=,EF=,
设P(t,﹣t2﹣t﹣2),
∴E(t﹣,﹣t2﹣t﹣2﹣),
∴﹣t2﹣t﹣2﹣=﹣×(t﹣)﹣2,
解得t=﹣1或t=﹣3,
∴P(﹣1,0)或P(﹣3,1);
(3)如图2,过点P作PH⊥x轴交于点H,
∵D点横坐标为﹣3,
∴D(﹣1,﹣3),
∴AD=3,AC=2,CD=,
∵AD2=AC2+CD2,
∴△ACD是直角三角形,
∴AD⊥CD,
∴tan∠CAD==,
设P(m,﹣m2﹣m﹣2),
∴PH=|﹣m2﹣m﹣2|,AH=|m+4|,
当∠PAH=∠CAD时,=,
∴3×|﹣m2﹣m﹣2|=|m+4|,
解得m=﹣或m=﹣,
∴P(﹣,)或P(﹣,﹣);
当∠APH=∠CAD时,=3,
∴|﹣m2﹣m﹣2|=3×|m+4|,
解得m=﹣7或m=5,
当m=﹣7时,∠PAB为钝角,
∴m=﹣7时不合题意,
∴P(5,﹣27)或P(﹣7,﹣9);
综上所述:P点的坐标为(﹣,)或(﹣,﹣)或(5,﹣27).
