2021-2022学年鲁教版(五四制)六年级数学上册3.6整式的加减 同步练习题 (Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册3.6整式的加减 同步练习题 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 141.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 09:29:56 | ||
图片预览

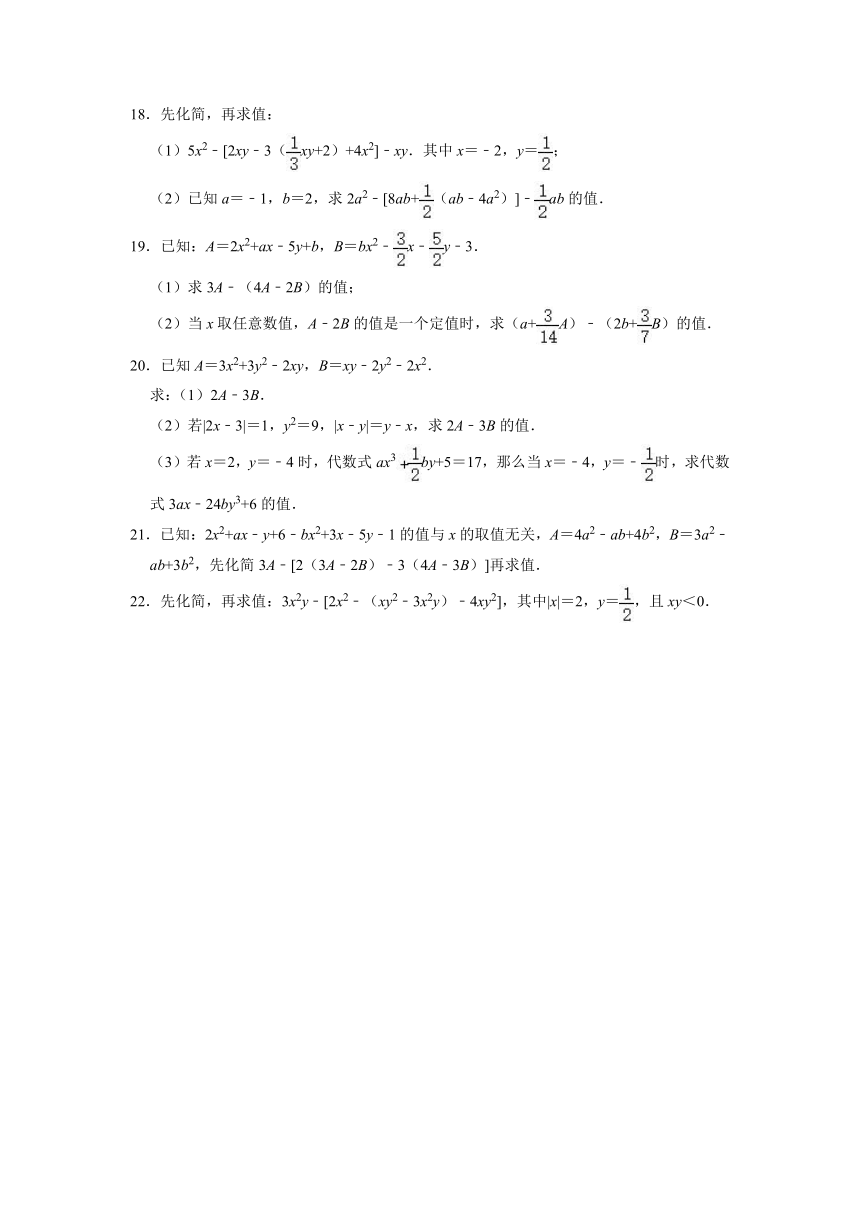

文档简介
2021-2022学年鲁教版六年级数学上册《3.6整式的加减》同步练习题(附答案)
一.选择题(共9小题,满分36分)
1.在代数式π,x2+,x+xy,3x2+nx+4,﹣x,3,5xy,中,整式共有( )
A.7个 B.6个 C.5个 D.4个
2.下列说法正确的是( )
A.单项式是整式,整式也是单项式 B.25与x5是同类项
C.单项式的系数是,次数是4 D.是一次二项式
3.下列各题中的两项是同类项的是( )
A.3x2y与﹣3x2y B.2a2b与0.2ab2
C.11abc与9bc D.62与x2
4.下列计算正确的是( )
A.﹣a3﹣a3=﹣2a3 B.4a2+a=5a2
C.4a﹣2a=2 D.2a2﹣a=a
5.如图,两个面积分别为35,23的图形叠放在一起,两个阴影部分的面积分别为a,b(a>b),则a﹣b的值为( )
A.6 B.8 C.9 D.12
6.如图1为2021年5月份的日历表,某同学任意框出了其中的四个数字,如图2,若用m表示框图中相应位置的数字,则“?”位置的数字可表示为( )
A.m+1 B.m+5 C.m+6 D.m+7
7.若式子2mx2﹣2x+8﹣(3x2﹣nx)的值与x无关,mn( )
A. B. C. D.
8.关于x,y的代数式(﹣3kxy+3y)+(9xy﹣8x+1)中不含二次项,则k=( )
A.4 B. C.3 D.
9.若m﹣x=2,n+y=3,则(m+n)﹣(x﹣y)=( )
A.﹣1 B.1 C.5 D.﹣5
二.填空题(共5小题,满分20分)
10.已知3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,则(﹣1)n+1= .
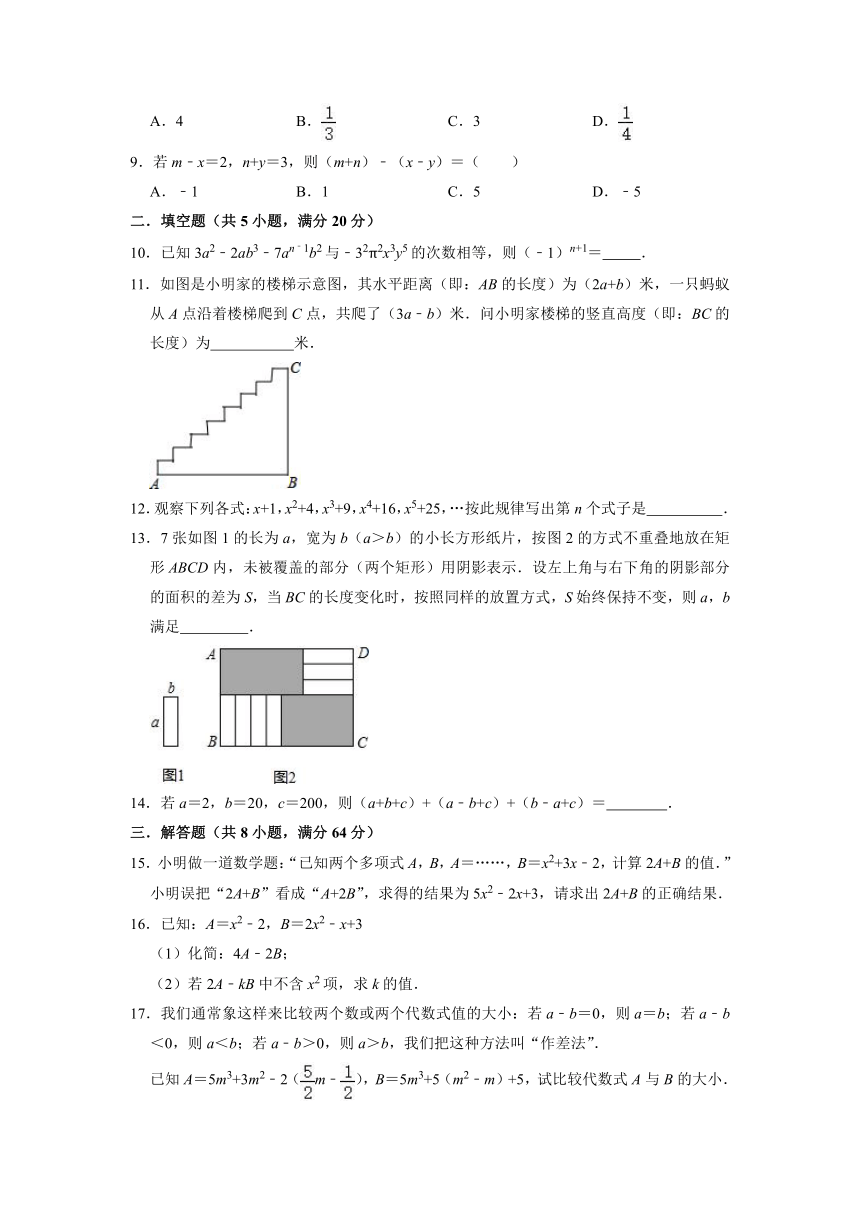
11.如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a﹣b)米.问小明家楼梯的竖直高度(即:BC的长度)为 米.
12.观察下列各式:x+1,x2+4,x3+9,x4+16,x5+25,…按此规律写出第n个式子是 .
13.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足 .
14.若a=2,b=20,c=200,则(a+b+c)+(a﹣b+c)+(b﹣a+c)= .
三.解答题(共8小题,满分64分)
15.小明做一道数学题:“已知两个多项式A,B,A=……,B=x2+3x﹣2,计算2A+B的值.”小明误把“2A+B”看成“A+2B”,求得的结果为5x2﹣2x+3,请求出2A+B的正确结果.
16.已知:A=x2﹣2,B=2x2﹣x+3
(1)化简:4A﹣2B;
(2)若2A﹣kB中不含x2项,求k的值.
17.我们通常象这样来比较两个数或两个代数式值的大小:若a﹣b=0,则a=b;若a﹣b<0,则a<b;若a﹣b>0,则a>b,我们把这种方法叫“作差法”.
已知A=5m3+3m2﹣2(m﹣),B=5m3+5(m2﹣m)+5,试比较代数式A与B的大小.
18.先化简,再求值:
(1)5x2﹣[2xy﹣3(xy+2)+4x2]﹣xy.其中x=﹣2,y=;
(2)已知a=﹣1,b=2,求2a2﹣[8ab+(ab﹣4a2)]﹣ab的值.
19.已知:A=2x2+ax﹣5y+b,B=bx2﹣x﹣y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+A)﹣(2b+B)的值.
20.已知A=3x2+3y2﹣2xy,B=xy﹣2y2﹣2x2.
求:(1)2A﹣3B.
(2)若|2x﹣3|=1,y2=9,|x﹣y|=y﹣x,求2A﹣3B的值.
(3)若x=2,y=﹣4时,代数式ax3by+5=17,那么当x=﹣4,y=﹣时,求代数式3ax﹣24by3+6的值.
21.已知:2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1的值与x的取值无关,A=4a2﹣ab+4b2,B=3a2﹣ab+3b2,先化简3A﹣[2(3A﹣2B)﹣3(4A﹣3B)]再求值.
22.先化简,再求值:3x2y﹣[2x2﹣(xy2﹣3x2y)﹣4xy2],其中|x|=2,y=,且xy<0.
参考答案
一.选择题(共9小题,满分36分)
1.解:在代数式π(单项式),x2+(分式),x+xy(多项式),3x2+nx+4(多项式),﹣x(单项式),3(单项式),5xy(单项式),(分式)中,整式共有6个,
故选:B.
2.解;A、整式包括单项式和多项式,所以单项式是整式,但整式不一定是单项式,故本选项错误;
B、25与x5指数相同,但底数不同,故本选项错误;
C、单项式的系数是,次数是4,正确;
D、中的不是整式,故本选项错误.
故选:C.
3.解:A、3x2y和﹣3x2y符合同类项的定义,是同类项;
B、2a2b与0.2ab2不符合同类项的定义,不是同类项;
C、﹣11abc与9bc不符合同类项的定义,不是同类项;
D、62与x2不符合同类项的定义,不是同类项.
故选:A.
4.解:A、﹣a3﹣a3=﹣2a3=(﹣1﹣1)a3=﹣2a3,故A正确;
B、不是同类项不能合并,故B错误;
C、4a﹣2a=(4﹣2)a=2a,故C错误;
D、不是同类项不能合并,故D错误.
故选:A.
5.解:设重叠部分的面积为c,
则a﹣b=(a+c)﹣(b+c)=35﹣23=12,
故选:D.
6.解:由题意得,“?”位置的数字可表示为m﹣1+7=m+6,
故选:C.
7.解:∵式子2mx2﹣2x+8﹣(3x2﹣nx)的值与x无关,
∴2m﹣3=0,﹣2+n=0,
解得:m=,n=2,
故mn=()2=.
故选:D.
8.解:∵关于x,y的代数式(﹣3kxy+3y)+(9xy﹣8x+1)中不含二次项,
∴﹣3k+9=0,
解得:k=3.
故选:C.
9.解:∵m﹣x=2,n+y=3,
∴m﹣x+n+y=5,
∴(m+n)﹣(x﹣y)=5.
故选:C.
二.填空题(共5小题,满分20分)
10.解:∵3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,
∴n﹣1+2=3+5,即n+1=8.
∴(﹣1)n+1=1.
11.解:(3a﹣b)﹣(2a+b)
=3a﹣b﹣2a﹣b
=a﹣2b(米).
故小明家楼梯的竖直高度(即:BC的长度)为 (a﹣2b)米.
故答案为:(a﹣2b).
12.解:x+1=x+12,
x2+4=x2+22,
x3+9=x3+32,
x4+16=x4+42,
x5+25=x5+52,
…
第n个式子是xn+n2.
故答案为:xn+n2.
13.解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AE AF﹣PC CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
故答案为:a=3b.
14.解:(a+b+c)+(a﹣b+c)+(b﹣a+c)
=a+b+c+a﹣b+c+b﹣a+c
=a+b+3c,
当a=2,b=20,c=200时,
原式=2+20+3×200=622.
故答案为:622.
三.解答题(共8小题,满分64分)
15.解:由题意可知:A+2B=5x2﹣2x+3,
∴A=(5x2﹣2x+3)﹣2(x2+3x﹣2)
=5x2﹣2x+3﹣2x2﹣6x+4
=3x2﹣8x+7,
∴2A+B
=2(3x2﹣8x+7)+(x2+3x﹣2)
=6x2﹣16x+14+x2+3x﹣2
=7x2﹣13x+12
16.解:(1)原式=4(x2﹣2)﹣2(2x2﹣x+3)
=4x2﹣8﹣4x2+2x﹣6
=2x﹣14
(2)2A﹣kB
=2(x2﹣2)﹣k(2x2﹣x+3)
=2x2﹣4﹣2kx2+kx﹣3k
∵2A﹣kB中不含x2项,
∴2﹣2k=0,
∴k=1
17.解:∵A=5m3+3m2﹣2(m﹣),B=5m3+5(m2﹣m)+5,
∴A﹣B=5m3+3m2﹣5m+1﹣5m3﹣5m2+5m﹣5=﹣2m2﹣4<0,
则A<B.
18.解:(1)原式=5x2﹣2xy+3(xy+2)﹣4x2﹣xy
=5x2﹣2xy+xy+6﹣4x2﹣xy
=x2﹣2xy+6,
当x=﹣2,y=时,
原式=(﹣2)2﹣2×(﹣2)×+6
=4+2+6
=12;
(2)原式=2a2﹣8ab﹣(ab﹣4a2)﹣ab
=2a2﹣8ab﹣ab+2a2﹣ab
=4a2﹣9ab,
当a=﹣1,b=2时,
原式=4×(﹣1)2﹣9×(﹣1)×2
=4+18
=22.
19.解:(1)∵A=2x2+ax﹣5y+b,B=bx2﹣x﹣y﹣3,
∴原式=3A﹣4A+2B=﹣A+2B=﹣2x2﹣ax+5y﹣b+2bx2﹣3x﹣5y﹣6=(2b﹣2)x2﹣(a+3)x﹣(b+6);
(2)∵A=2x2+ax﹣5y+b,B=bx2﹣x﹣y﹣3,
∴A﹣2B=2x2+ax﹣5y+b﹣2bx2+3x+5y+6=(2﹣2b)x2+(a+3)x+(b+6),
由x取任意数值时,A﹣2B的值是一个定值,得到2﹣2b=0,a+3=0,
解得:a=﹣3,b=1,
则原式=a﹣2b+(A﹣2B)=﹣3﹣2+=﹣3.
20.解:(1)2A﹣3B
=2(3x2+3y2﹣2xy)﹣3(xy﹣2y2﹣2x2)
=6x2+6y2﹣4xy﹣3xy+6y2+6x2
=12x2+12y2﹣7xy;
(2)∵|2x﹣3|=1,y2=9,
∴x1=2,x2=1,y1=3,y2=﹣3
又∵|x﹣y|=y﹣x,
∴x1=2,x2=1,y=3.
当x=2,y=3时,2A﹣3B
=12x2+12y2﹣7xy
=12×4+12×9﹣7×2×3
=114;
当x=1,y=3时,2A﹣3B
=12x2+12y2﹣7xy
=12×1+12×9﹣7×1×3
=99.
(3)∵x=2,y=﹣4时,代数式ax3by+5=17,
∴8a﹣2b=12,即4a﹣b=6.
当x=﹣4,y=﹣时,
代数式3ax﹣24by3+6
=﹣12a+3b+6
=﹣3(4a﹣b)+6
∵4a﹣b=6,
∴原式=﹣3×6+6
=﹣12.
21.解:2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1=(2﹣b)x2+(a+3)x﹣6y+5,
由结果与x的取值无关,得到2﹣b=0,a+3=0,
解得:a=﹣3,b=2,
则原式=3A﹣6A+4B+12A﹣9B=9A﹣5B=36a2﹣9ab+36b2﹣15a2+5ab﹣15b2=21a2﹣4ab+21b2=189+24+84=297.
22.解:原式=3x2y﹣2x2+xy2﹣3x2y+4xy2=5xy2﹣2x2,
∵|x|=2,y=,且xy<0,
∴x=﹣2,y=,
则原式=﹣﹣8=﹣.
一.选择题(共9小题,满分36分)
1.在代数式π,x2+,x+xy,3x2+nx+4,﹣x,3,5xy,中,整式共有( )
A.7个 B.6个 C.5个 D.4个
2.下列说法正确的是( )
A.单项式是整式,整式也是单项式 B.25与x5是同类项
C.单项式的系数是,次数是4 D.是一次二项式
3.下列各题中的两项是同类项的是( )
A.3x2y与﹣3x2y B.2a2b与0.2ab2
C.11abc与9bc D.62与x2
4.下列计算正确的是( )
A.﹣a3﹣a3=﹣2a3 B.4a2+a=5a2
C.4a﹣2a=2 D.2a2﹣a=a
5.如图,两个面积分别为35,23的图形叠放在一起,两个阴影部分的面积分别为a,b(a>b),则a﹣b的值为( )
A.6 B.8 C.9 D.12
6.如图1为2021年5月份的日历表,某同学任意框出了其中的四个数字,如图2,若用m表示框图中相应位置的数字,则“?”位置的数字可表示为( )
A.m+1 B.m+5 C.m+6 D.m+7
7.若式子2mx2﹣2x+8﹣(3x2﹣nx)的值与x无关,mn( )
A. B. C. D.
8.关于x,y的代数式(﹣3kxy+3y)+(9xy﹣8x+1)中不含二次项,则k=( )
A.4 B. C.3 D.
9.若m﹣x=2,n+y=3,则(m+n)﹣(x﹣y)=( )
A.﹣1 B.1 C.5 D.﹣5
二.填空题(共5小题,满分20分)
10.已知3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,则(﹣1)n+1= .
11.如图是小明家的楼梯示意图,其水平距离(即:AB的长度)为(2a+b)米,一只蚂蚁从A点沿着楼梯爬到C点,共爬了(3a﹣b)米.问小明家楼梯的竖直高度(即:BC的长度)为 米.
12.观察下列各式:x+1,x2+4,x3+9,x4+16,x5+25,…按此规律写出第n个式子是 .
13.7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足 .
14.若a=2,b=20,c=200,则(a+b+c)+(a﹣b+c)+(b﹣a+c)= .
三.解答题(共8小题,满分64分)
15.小明做一道数学题:“已知两个多项式A,B,A=……,B=x2+3x﹣2,计算2A+B的值.”小明误把“2A+B”看成“A+2B”,求得的结果为5x2﹣2x+3,请求出2A+B的正确结果.
16.已知:A=x2﹣2,B=2x2﹣x+3
(1)化简:4A﹣2B;
(2)若2A﹣kB中不含x2项,求k的值.
17.我们通常象这样来比较两个数或两个代数式值的大小:若a﹣b=0,则a=b;若a﹣b<0,则a<b;若a﹣b>0,则a>b,我们把这种方法叫“作差法”.
已知A=5m3+3m2﹣2(m﹣),B=5m3+5(m2﹣m)+5,试比较代数式A与B的大小.
18.先化简,再求值:
(1)5x2﹣[2xy﹣3(xy+2)+4x2]﹣xy.其中x=﹣2,y=;
(2)已知a=﹣1,b=2,求2a2﹣[8ab+(ab﹣4a2)]﹣ab的值.
19.已知:A=2x2+ax﹣5y+b,B=bx2﹣x﹣y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+A)﹣(2b+B)的值.
20.已知A=3x2+3y2﹣2xy,B=xy﹣2y2﹣2x2.
求:(1)2A﹣3B.
(2)若|2x﹣3|=1,y2=9,|x﹣y|=y﹣x,求2A﹣3B的值.
(3)若x=2,y=﹣4时,代数式ax3by+5=17,那么当x=﹣4,y=﹣时,求代数式3ax﹣24by3+6的值.
21.已知:2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1的值与x的取值无关,A=4a2﹣ab+4b2,B=3a2﹣ab+3b2,先化简3A﹣[2(3A﹣2B)﹣3(4A﹣3B)]再求值.
22.先化简,再求值:3x2y﹣[2x2﹣(xy2﹣3x2y)﹣4xy2],其中|x|=2,y=,且xy<0.
参考答案
一.选择题(共9小题,满分36分)
1.解:在代数式π(单项式),x2+(分式),x+xy(多项式),3x2+nx+4(多项式),﹣x(单项式),3(单项式),5xy(单项式),(分式)中,整式共有6个,
故选:B.
2.解;A、整式包括单项式和多项式,所以单项式是整式,但整式不一定是单项式,故本选项错误;
B、25与x5指数相同,但底数不同,故本选项错误;
C、单项式的系数是,次数是4,正确;
D、中的不是整式,故本选项错误.
故选:C.
3.解:A、3x2y和﹣3x2y符合同类项的定义,是同类项;
B、2a2b与0.2ab2不符合同类项的定义,不是同类项;
C、﹣11abc与9bc不符合同类项的定义,不是同类项;
D、62与x2不符合同类项的定义,不是同类项.
故选:A.
4.解:A、﹣a3﹣a3=﹣2a3=(﹣1﹣1)a3=﹣2a3,故A正确;
B、不是同类项不能合并,故B错误;
C、4a﹣2a=(4﹣2)a=2a,故C错误;
D、不是同类项不能合并,故D错误.
故选:A.
5.解:设重叠部分的面积为c,
则a﹣b=(a+c)﹣(b+c)=35﹣23=12,
故选:D.
6.解:由题意得,“?”位置的数字可表示为m﹣1+7=m+6,
故选:C.
7.解:∵式子2mx2﹣2x+8﹣(3x2﹣nx)的值与x无关,
∴2m﹣3=0,﹣2+n=0,
解得:m=,n=2,
故mn=()2=.
故选:D.
8.解:∵关于x,y的代数式(﹣3kxy+3y)+(9xy﹣8x+1)中不含二次项,
∴﹣3k+9=0,
解得:k=3.
故选:C.
9.解:∵m﹣x=2,n+y=3,
∴m﹣x+n+y=5,
∴(m+n)﹣(x﹣y)=5.
故选:C.
二.填空题(共5小题,满分20分)
10.解:∵3a2﹣2ab3﹣7an﹣1b2与﹣32π2x3y5的次数相等,
∴n﹣1+2=3+5,即n+1=8.
∴(﹣1)n+1=1.
11.解:(3a﹣b)﹣(2a+b)
=3a﹣b﹣2a﹣b
=a﹣2b(米).
故小明家楼梯的竖直高度(即:BC的长度)为 (a﹣2b)米.
故答案为:(a﹣2b).
12.解:x+1=x+12,
x2+4=x2+22,
x3+9=x3+32,
x4+16=x4+42,
x5+25=x5+52,
…
第n个式子是xn+n2.
故答案为:xn+n2.
13.解:左上角阴影部分的长为AE,宽为AF=3b,右下角阴影部分的长为PC,宽为a,
∵AD=BC,即AE+ED=AE+a,BC=BP+PC=4b+PC,
∴AE+a=4b+PC,即AE﹣PC=4b﹣a,
∴阴影部分面积之差S=AE AF﹣PC CG=3bAE﹣aPC=3b(PC+4b﹣a)﹣aPC=(3b﹣a)PC+12b2﹣3ab,
则3b﹣a=0,即a=3b.
故答案为:a=3b.
14.解:(a+b+c)+(a﹣b+c)+(b﹣a+c)
=a+b+c+a﹣b+c+b﹣a+c
=a+b+3c,
当a=2,b=20,c=200时,
原式=2+20+3×200=622.
故答案为:622.
三.解答题(共8小题,满分64分)
15.解:由题意可知:A+2B=5x2﹣2x+3,
∴A=(5x2﹣2x+3)﹣2(x2+3x﹣2)
=5x2﹣2x+3﹣2x2﹣6x+4
=3x2﹣8x+7,
∴2A+B
=2(3x2﹣8x+7)+(x2+3x﹣2)
=6x2﹣16x+14+x2+3x﹣2
=7x2﹣13x+12
16.解:(1)原式=4(x2﹣2)﹣2(2x2﹣x+3)
=4x2﹣8﹣4x2+2x﹣6
=2x﹣14
(2)2A﹣kB
=2(x2﹣2)﹣k(2x2﹣x+3)
=2x2﹣4﹣2kx2+kx﹣3k
∵2A﹣kB中不含x2项,
∴2﹣2k=0,
∴k=1
17.解:∵A=5m3+3m2﹣2(m﹣),B=5m3+5(m2﹣m)+5,
∴A﹣B=5m3+3m2﹣5m+1﹣5m3﹣5m2+5m﹣5=﹣2m2﹣4<0,
则A<B.
18.解:(1)原式=5x2﹣2xy+3(xy+2)﹣4x2﹣xy
=5x2﹣2xy+xy+6﹣4x2﹣xy
=x2﹣2xy+6,
当x=﹣2,y=时,
原式=(﹣2)2﹣2×(﹣2)×+6
=4+2+6
=12;
(2)原式=2a2﹣8ab﹣(ab﹣4a2)﹣ab
=2a2﹣8ab﹣ab+2a2﹣ab
=4a2﹣9ab,
当a=﹣1,b=2时,
原式=4×(﹣1)2﹣9×(﹣1)×2
=4+18
=22.
19.解:(1)∵A=2x2+ax﹣5y+b,B=bx2﹣x﹣y﹣3,
∴原式=3A﹣4A+2B=﹣A+2B=﹣2x2﹣ax+5y﹣b+2bx2﹣3x﹣5y﹣6=(2b﹣2)x2﹣(a+3)x﹣(b+6);
(2)∵A=2x2+ax﹣5y+b,B=bx2﹣x﹣y﹣3,
∴A﹣2B=2x2+ax﹣5y+b﹣2bx2+3x+5y+6=(2﹣2b)x2+(a+3)x+(b+6),
由x取任意数值时,A﹣2B的值是一个定值,得到2﹣2b=0,a+3=0,
解得:a=﹣3,b=1,
则原式=a﹣2b+(A﹣2B)=﹣3﹣2+=﹣3.
20.解:(1)2A﹣3B
=2(3x2+3y2﹣2xy)﹣3(xy﹣2y2﹣2x2)
=6x2+6y2﹣4xy﹣3xy+6y2+6x2
=12x2+12y2﹣7xy;
(2)∵|2x﹣3|=1,y2=9,
∴x1=2,x2=1,y1=3,y2=﹣3
又∵|x﹣y|=y﹣x,
∴x1=2,x2=1,y=3.
当x=2,y=3时,2A﹣3B
=12x2+12y2﹣7xy
=12×4+12×9﹣7×2×3
=114;
当x=1,y=3时,2A﹣3B
=12x2+12y2﹣7xy
=12×1+12×9﹣7×1×3
=99.
(3)∵x=2,y=﹣4时,代数式ax3by+5=17,
∴8a﹣2b=12,即4a﹣b=6.
当x=﹣4,y=﹣时,
代数式3ax﹣24by3+6
=﹣12a+3b+6
=﹣3(4a﹣b)+6
∵4a﹣b=6,
∴原式=﹣3×6+6
=﹣12.
21.解:2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1=(2﹣b)x2+(a+3)x﹣6y+5,
由结果与x的取值无关,得到2﹣b=0,a+3=0,
解得:a=﹣3,b=2,
则原式=3A﹣6A+4B+12A﹣9B=9A﹣5B=36a2﹣9ab+36b2﹣15a2+5ab﹣15b2=21a2﹣4ab+21b2=189+24+84=297.
22.解:原式=3x2y﹣2x2+xy2﹣3x2y+4xy2=5xy2﹣2x2,
∵|x|=2,y=,且xy<0,
∴x=﹣2,y=,
则原式=﹣﹣8=﹣.
