2021-2022学年鲁教版(五四制)六年级数学上册第3章整式及其加减 单元达标测评 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学上册第3章整式及其加减 单元达标测评 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 106.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 10:37:42 | ||
图片预览



文档简介
2021-2022学年鲁教版六年级数学上册《第3章整式及其加减》单元达标测评(附答案)
一.选择题(共8小题,满分32分)
1.下列各式,去括号正确的是( )
A.a+(b﹣c)+d=a﹣b+c﹣d B.a﹣(b﹣c+d)=a﹣b﹣c+d
C.a﹣(b﹣c+d)=a﹣b+c﹣d D.a﹣(b﹣c+d)=a﹣b+c+d
2.下列各组中,不是同类项的是( )
A.52与25 B.﹣ab与ba
C.0.2a2b与﹣a2b D.a2b3与﹣a3b2
3.下列计算正确的是( )
A.x2+x2=x4 B.x2+x3=2x5
C.3x﹣2x=1 D.x2y﹣2x2y=﹣x2y
4.若a﹣b=1,则代数式2a﹣2b﹣1的值为( )
A.1 B.﹣1 C.2 D.﹣2
5.某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )
A.(a+15%)(a﹣5%)万元 B.(a﹣15%)(a+5%)万元
C.a(1+15%)(1﹣5%)万元 D.a(1﹣15%)(1+5%)万元
6.将正整数按如图所示的位置顺序排列:
根据排列规律,则2021应在( )
A.A处 B.B处 C.C处 D.D处
7.用大小相同的圆点摆成如图所示的图案,按照这样的规律摆放,则第10个图案中共有圆点的个数是( )
A.59 B.65 C.70 D.71
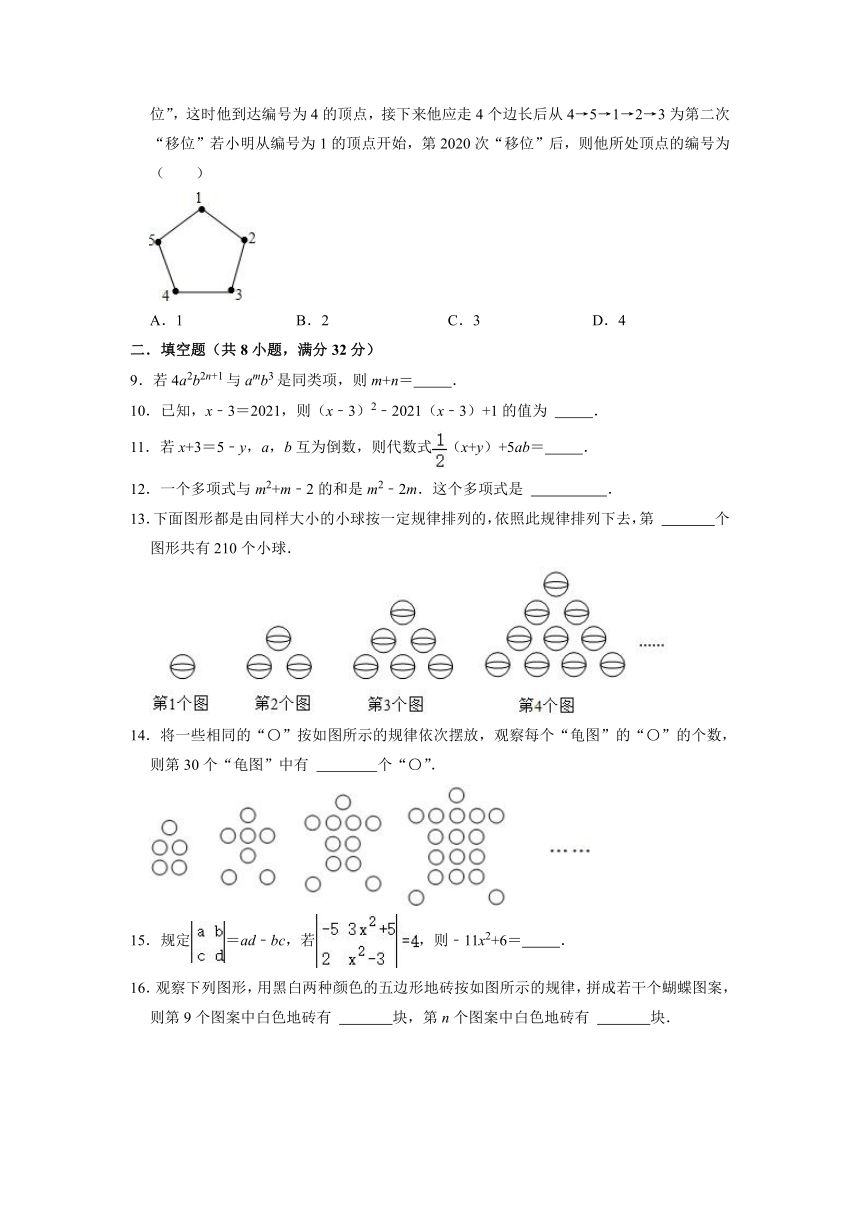
8.如图,给正五边形的顶点依次编号为1,2,3,4,5,若从某一个顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”,如:小明在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点,接下来他应走4个边长后从4→5→1→2→3为第二次“移位”若小明从编号为1的顶点开始,第2020次“移位”后,则他所处顶点的编号为( )
A.1 B.2 C.3 D.4
二.填空题(共8小题,满分32分)
9.若4a2b2n+1与amb3是同类项,则m+n= .
10.已知,x﹣3=2021,则(x﹣3)2﹣2021(x﹣3)+1的值为 .
11.若x+3=5﹣y,a,b互为倒数,则代数式(x+y)+5ab= .
12.一个多项式与m2+m﹣2的和是m2﹣2m.这个多项式是 .
13.下面图形都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第 个图形共有210个小球.
14.将一些相同的“〇”按如图所示的规律依次摆放,观察每个“龟图”的“〇”的个数,则第30个“龟图”中有 个“〇”.
15.规定=ad﹣bc,若,则﹣11x2+6= .
16.观察下列图形,用黑白两种颜色的五边形地砖按如图所示的规律,拼成若干个蝴蝶图案,则第9个图案中白色地砖有 块,第n个图案中白色地砖有 块.
三.解答题(共6小题,满分56分)
17.先化简,再求值:2(xy+5x2y)﹣3(3xy2﹣xy)﹣xy2,其中x,y满足x=﹣1,y=﹣.
18.先化简,再求值:5a2b﹣2(a2b﹣2ab2+1)+3(﹣2ab2+a2b),其中a=﹣2,b=1.
19.已知代数式A=3x2﹣x+1,马小虎同学在做整式加减运算时,误将“A﹣B”看成“A+B”了,计算的结果是2x2﹣3x﹣2.
(1)请你帮马小虎同学求出正确的结果;
(2)x是最大的负整数,将x代入(1)问的结果求值.
20.某商场销售进价为每件x元的上衣,先按进价的2倍作为定价,而实际销售时按定价打八折出售.
(1)试用代数式表示:
①每件上衣最初的定价为 元;
②每件上衣打八折后的销售价为 元;
③n件上衣打八折后的利润为 元;
(2)若该商场这次共购进每件120元的上衣100件,按以上办法售出80件后,其余按定价的六折销售全部卖完,问该商场在这批上衣买卖中,除支付销售费用1000元外,盈亏情况如何?
21.观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,第n层有 个小圆圈.
(2)某一层上有65个圆圈,这是第 层.
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.
同样:
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
…
根据上述规律,从1开始的n个连续奇数之和是多少?用n的代数式把它表示出来 .
(4)运用(3)中的规律计算:73+75+77+…+153.
22.已知代数式A=a4﹣3a2b2﹣ab3+5,B=2b4﹣2a2b2+ab3,C=a4﹣5a2b2+2b4﹣2.
小丽说:“代数式A+B﹣C的值与a,b的值无关.”她说得对吗?说说你的理由.
参考答案
一.选择题(共8小题,满分32分)
1.解:A、a+(b﹣c)+d=a+b﹣c+d,故错误;
B、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
D、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
只有C符合运算方法,正确.
故选:C.
2.解:不是同类项的是a2b3与﹣a3b2.
故选:D.
3.解:A、原式=2x2,错误;
B、原式不能合并,错误;
C、原式=x,错误;
D、原式=﹣x2y,正确,
故选:D.
4.解:∵a﹣b=1,
∴2a﹣2b﹣1
=2(a﹣b)﹣1
=2×1﹣1
=2﹣1
=1.
故选:A.
5.解:∵今年1月份产值为a万元,2月份比1月份减少了15%,
∴2月份的产值为a(1﹣15%)万元,
∵3月份比2月份增加了5%,
∴3月份的产值为a(1﹣15%)(1+5%)万元.
故选:D.
6.解:2021÷4=505…1,
∴2021应在1的位置,也就是在D处.
故选:D.
7.解:根据图中圆点排列,当n=1时,圆点个数5+2;当n=2时,圆点个数5+2+3;当n=3时,圆点个数5+2+3+4;当n=4时,圆点个数5+2+3+4+5,…
∴当n=10时,圆点个数5+2+3+4+5+6+7+8+9+10+11=4+(1+2+3+4+5+6+7+8+9+10+11)=.
故选:C.
8.解:根据题意,小明从编号为1的顶点开始,第1次移位到点2,
第2次移位到点4,
第3次移位到达点3,
第4次移位到达点1,
第5次移位到达点2,
…,
依此类推,4次移位后回到出发点,
∵2020÷4=505,
∴第2020次“移位“后,它所处顶点的编号与第4次移位到的编号相同,为1,
故选:A.
二.填空题(共8小题,满分32分)
9.解:∵4a2b2n+1与amb3是同类项,
∴,
∴,
∴m+n=3,
故答案为3.
10.解:∵x﹣3=2021,
∴(x﹣3)2﹣2021(x﹣3)+1
=20212﹣2021×2021+1
=1,
故答案为:1.
11.解:由题意可知:x+3=5﹣y,ab=1,
∴x+y=2,ab=1,
∴原式=1+5=6,
故答案为:6
12.解:∵一多项式与m2+m﹣2的和是m2﹣2m.
∴这个多项式是:m2﹣2m﹣(m2+m﹣2)=﹣3m+2.
故答案为:﹣3m+2.
13.解:第1个图中有1个小球,
第2个图中有3个小球,3=1+2,
第3个图中有6个小球,6=1+2+3,
第4个图中有10个小球,10=1+2+3+4,
……
照此规律,第n个图中有1+2+3+……+n=个小球,
当时,
解之得:n1=20,n2=﹣21(舍),
故答案为:20.
14.解:∵第1个图形中小圆的个数为1+4=5;
第2个图形中小圆的个数为1+5+1=7;
第3个图形中小圆的个数为1+6+4=11;
第4个图形中小圆的个数为1+7+9=17;
…
∴第n个图形中小圆的个数为1+(n+3)+(n﹣1)2.
∴第30个“龟图”中的“〇”的个数为1+(30+3)+(30﹣1)2=1+33+841=875.
另一种解法:∵第1个图形中小圆的个数为0+5=5;
第2个图形中小圆的个数为2+5=1×2+5=7;
第3个图形中小圆的个数为6+5=2×3+5=11;
第4个图形中小圆的个数为12+5=3×4+5=17;
…
∴第n个图形中小圆的个数为n(n﹣1)+5.
∴第30个“龟图”中的“〇”的个数为30×(30﹣1)+5=875.
故答案为:875.
15.解:根据题中的新定义化简得:﹣5(x2﹣3)﹣2(3x2+5)=4,
去括号得:﹣5x2+15﹣6x2﹣10=4,
移项合并得:﹣11x2=﹣1,
则原式=﹣1+6=5,
故答案为:5
16.解:设第n(n为正整数)幅蝴蝶图案中有an块白色地砖.
观察图形,可知:a1=4=3×1+1,a2=7=3×2+1,a3=10=3×3+1,…,
∴an=3n+1,
∴a9=3×9+1=28.
故答案为:28;(3n+1).
三.解答题(共6小题,满分56分)
17.解:原式=2xy+10x2y﹣9xy2+3xy﹣xy2
=10x2y﹣10xy2+5xy,
当x=﹣1,y=﹣时,
原式=10×(﹣1)2×(﹣)﹣10×(﹣1)×(﹣)2+5×(﹣1)×(﹣)
=﹣5﹣(﹣)+
=﹣5++
=0.
18.解:原式=5a2b﹣2a2b+4ab2﹣2﹣6ab2+3a2b
=6a2b﹣2ab2﹣2
=2ab(3a﹣b)﹣2,
把a=﹣2,b=1代入上式,
原式=2×(﹣2)×1×[3×(﹣2)﹣1]﹣2=26.
19.解:(1)根据题意知B=2x2﹣3x﹣2﹣(3x2﹣x+1)
=2x2﹣3x﹣2﹣3x2+x﹣1
=﹣x2﹣2x﹣3,
则A﹣B=(3x2﹣x+1)﹣(﹣x2﹣2x﹣3)
=3x2﹣x+1+x2+2x+3
=4x2+x+4;
(2)∵x是最大的负整数,
∴x=﹣1,
则原式=4×(﹣1)2﹣1+4
=4﹣1+4
=7.
20.解:(1)①每件上衣最初的定价为2x(元);
②每件上衣打八折后的销售价为2x 0.8=1.6x(元);
③n件上衣打八折后的利润为 n (1.6x﹣x)=0.6xn(元);
(2)0.6×120×80+2×120×0.6×20﹣120×20﹣1000=5240(元),
所以该商场在这批上衣买卖中盈利5240元.
故答案为2x,1.6x,06xn.
21.解:(1)第n层有(2n﹣1)个小圆圈;
故答案为:(2n﹣1);
(2)令2n﹣1=65,
解得n=33.
所以这是第33层;
故答案为:33;
(3)1+3+5+…+(2n﹣1)=n2;
故答案为:n2;
(4)(1+3+5+…+153)﹣(1+3+5+…+71)
=()2﹣()2
=772﹣362
=4633.
22.解:小丽的说法正确,理由如下:
∵A=a4﹣3a2b2﹣ab3+5,B=2b4﹣2a2b2+ab3,C=a4﹣5a2b2+2b4﹣2,
∴A+B﹣C=(a4﹣3a2b2﹣ab3+5)+(2b4﹣2a2b2+ab3)﹣(a4﹣5a2b2+2b4﹣2)
=a4﹣3a2b2﹣ab3+5+2b4﹣2a2b2+ab3﹣a4+5a2b2﹣2b4+2
=7,
则结果为常数,与a,b的值无关.
一.选择题(共8小题,满分32分)
1.下列各式,去括号正确的是( )
A.a+(b﹣c)+d=a﹣b+c﹣d B.a﹣(b﹣c+d)=a﹣b﹣c+d
C.a﹣(b﹣c+d)=a﹣b+c﹣d D.a﹣(b﹣c+d)=a﹣b+c+d
2.下列各组中,不是同类项的是( )
A.52与25 B.﹣ab与ba
C.0.2a2b与﹣a2b D.a2b3与﹣a3b2
3.下列计算正确的是( )
A.x2+x2=x4 B.x2+x3=2x5
C.3x﹣2x=1 D.x2y﹣2x2y=﹣x2y
4.若a﹣b=1,则代数式2a﹣2b﹣1的值为( )
A.1 B.﹣1 C.2 D.﹣2
5.某企业今年1月份产值为a万元,2月份比1月份减少了15%,3月份比2月份增加了5%,则3月份的产值为( )
A.(a+15%)(a﹣5%)万元 B.(a﹣15%)(a+5%)万元
C.a(1+15%)(1﹣5%)万元 D.a(1﹣15%)(1+5%)万元
6.将正整数按如图所示的位置顺序排列:
根据排列规律,则2021应在( )
A.A处 B.B处 C.C处 D.D处
7.用大小相同的圆点摆成如图所示的图案,按照这样的规律摆放,则第10个图案中共有圆点的个数是( )
A.59 B.65 C.70 D.71
8.如图,给正五边形的顶点依次编号为1,2,3,4,5,若从某一个顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”,如:小明在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点,接下来他应走4个边长后从4→5→1→2→3为第二次“移位”若小明从编号为1的顶点开始,第2020次“移位”后,则他所处顶点的编号为( )
A.1 B.2 C.3 D.4
二.填空题(共8小题,满分32分)
9.若4a2b2n+1与amb3是同类项,则m+n= .
10.已知,x﹣3=2021,则(x﹣3)2﹣2021(x﹣3)+1的值为 .
11.若x+3=5﹣y,a,b互为倒数,则代数式(x+y)+5ab= .
12.一个多项式与m2+m﹣2的和是m2﹣2m.这个多项式是 .
13.下面图形都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第 个图形共有210个小球.
14.将一些相同的“〇”按如图所示的规律依次摆放,观察每个“龟图”的“〇”的个数,则第30个“龟图”中有 个“〇”.
15.规定=ad﹣bc,若,则﹣11x2+6= .
16.观察下列图形,用黑白两种颜色的五边形地砖按如图所示的规律,拼成若干个蝴蝶图案,则第9个图案中白色地砖有 块,第n个图案中白色地砖有 块.
三.解答题(共6小题,满分56分)
17.先化简,再求值:2(xy+5x2y)﹣3(3xy2﹣xy)﹣xy2,其中x,y满足x=﹣1,y=﹣.
18.先化简,再求值:5a2b﹣2(a2b﹣2ab2+1)+3(﹣2ab2+a2b),其中a=﹣2,b=1.
19.已知代数式A=3x2﹣x+1,马小虎同学在做整式加减运算时,误将“A﹣B”看成“A+B”了,计算的结果是2x2﹣3x﹣2.
(1)请你帮马小虎同学求出正确的结果;
(2)x是最大的负整数,将x代入(1)问的结果求值.
20.某商场销售进价为每件x元的上衣,先按进价的2倍作为定价,而实际销售时按定价打八折出售.
(1)试用代数式表示:
①每件上衣最初的定价为 元;
②每件上衣打八折后的销售价为 元;
③n件上衣打八折后的利润为 元;
(2)若该商场这次共购进每件120元的上衣100件,按以上办法售出80件后,其余按定价的六折销售全部卖完,问该商场在这批上衣买卖中,除支付销售费用1000元外,盈亏情况如何?
21.观察图,解答下列问题.
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,第n层有 个小圆圈.
(2)某一层上有65个圆圈,这是第 层.
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3=22.
同样:
由前三层的圆圈个数和得:1+3+5=32.
由前四层的圆圈个数和得:1+3+5+7=42.
…
根据上述规律,从1开始的n个连续奇数之和是多少?用n的代数式把它表示出来 .
(4)运用(3)中的规律计算:73+75+77+…+153.
22.已知代数式A=a4﹣3a2b2﹣ab3+5,B=2b4﹣2a2b2+ab3,C=a4﹣5a2b2+2b4﹣2.
小丽说:“代数式A+B﹣C的值与a,b的值无关.”她说得对吗?说说你的理由.
参考答案
一.选择题(共8小题,满分32分)
1.解:A、a+(b﹣c)+d=a+b﹣c+d,故错误;
B、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
D、a﹣(b﹣c+d)=a﹣b+c﹣d,故错误;
只有C符合运算方法,正确.
故选:C.
2.解:不是同类项的是a2b3与﹣a3b2.
故选:D.
3.解:A、原式=2x2,错误;
B、原式不能合并,错误;
C、原式=x,错误;
D、原式=﹣x2y,正确,
故选:D.
4.解:∵a﹣b=1,
∴2a﹣2b﹣1
=2(a﹣b)﹣1
=2×1﹣1
=2﹣1
=1.
故选:A.
5.解:∵今年1月份产值为a万元,2月份比1月份减少了15%,
∴2月份的产值为a(1﹣15%)万元,
∵3月份比2月份增加了5%,
∴3月份的产值为a(1﹣15%)(1+5%)万元.
故选:D.
6.解:2021÷4=505…1,
∴2021应在1的位置,也就是在D处.
故选:D.
7.解:根据图中圆点排列,当n=1时,圆点个数5+2;当n=2时,圆点个数5+2+3;当n=3时,圆点个数5+2+3+4;当n=4时,圆点个数5+2+3+4+5,…
∴当n=10时,圆点个数5+2+3+4+5+6+7+8+9+10+11=4+(1+2+3+4+5+6+7+8+9+10+11)=.
故选:C.
8.解:根据题意,小明从编号为1的顶点开始,第1次移位到点2,
第2次移位到点4,
第3次移位到达点3,
第4次移位到达点1,
第5次移位到达点2,
…,
依此类推,4次移位后回到出发点,
∵2020÷4=505,
∴第2020次“移位“后,它所处顶点的编号与第4次移位到的编号相同,为1,
故选:A.
二.填空题(共8小题,满分32分)
9.解:∵4a2b2n+1与amb3是同类项,
∴,
∴,
∴m+n=3,
故答案为3.
10.解:∵x﹣3=2021,
∴(x﹣3)2﹣2021(x﹣3)+1
=20212﹣2021×2021+1
=1,
故答案为:1.
11.解:由题意可知:x+3=5﹣y,ab=1,
∴x+y=2,ab=1,
∴原式=1+5=6,
故答案为:6
12.解:∵一多项式与m2+m﹣2的和是m2﹣2m.
∴这个多项式是:m2﹣2m﹣(m2+m﹣2)=﹣3m+2.
故答案为:﹣3m+2.
13.解:第1个图中有1个小球,
第2个图中有3个小球,3=1+2,
第3个图中有6个小球,6=1+2+3,
第4个图中有10个小球,10=1+2+3+4,
……
照此规律,第n个图中有1+2+3+……+n=个小球,
当时,
解之得:n1=20,n2=﹣21(舍),
故答案为:20.
14.解:∵第1个图形中小圆的个数为1+4=5;
第2个图形中小圆的个数为1+5+1=7;
第3个图形中小圆的个数为1+6+4=11;
第4个图形中小圆的个数为1+7+9=17;
…
∴第n个图形中小圆的个数为1+(n+3)+(n﹣1)2.
∴第30个“龟图”中的“〇”的个数为1+(30+3)+(30﹣1)2=1+33+841=875.
另一种解法:∵第1个图形中小圆的个数为0+5=5;
第2个图形中小圆的个数为2+5=1×2+5=7;
第3个图形中小圆的个数为6+5=2×3+5=11;
第4个图形中小圆的个数为12+5=3×4+5=17;
…
∴第n个图形中小圆的个数为n(n﹣1)+5.
∴第30个“龟图”中的“〇”的个数为30×(30﹣1)+5=875.
故答案为:875.
15.解:根据题中的新定义化简得:﹣5(x2﹣3)﹣2(3x2+5)=4,
去括号得:﹣5x2+15﹣6x2﹣10=4,
移项合并得:﹣11x2=﹣1,
则原式=﹣1+6=5,
故答案为:5
16.解:设第n(n为正整数)幅蝴蝶图案中有an块白色地砖.
观察图形,可知:a1=4=3×1+1,a2=7=3×2+1,a3=10=3×3+1,…,
∴an=3n+1,
∴a9=3×9+1=28.
故答案为:28;(3n+1).
三.解答题(共6小题,满分56分)
17.解:原式=2xy+10x2y﹣9xy2+3xy﹣xy2
=10x2y﹣10xy2+5xy,
当x=﹣1,y=﹣时,
原式=10×(﹣1)2×(﹣)﹣10×(﹣1)×(﹣)2+5×(﹣1)×(﹣)
=﹣5﹣(﹣)+
=﹣5++
=0.
18.解:原式=5a2b﹣2a2b+4ab2﹣2﹣6ab2+3a2b
=6a2b﹣2ab2﹣2
=2ab(3a﹣b)﹣2,
把a=﹣2,b=1代入上式,
原式=2×(﹣2)×1×[3×(﹣2)﹣1]﹣2=26.
19.解:(1)根据题意知B=2x2﹣3x﹣2﹣(3x2﹣x+1)
=2x2﹣3x﹣2﹣3x2+x﹣1
=﹣x2﹣2x﹣3,
则A﹣B=(3x2﹣x+1)﹣(﹣x2﹣2x﹣3)
=3x2﹣x+1+x2+2x+3
=4x2+x+4;
(2)∵x是最大的负整数,
∴x=﹣1,
则原式=4×(﹣1)2﹣1+4
=4﹣1+4
=7.
20.解:(1)①每件上衣最初的定价为2x(元);
②每件上衣打八折后的销售价为2x 0.8=1.6x(元);
③n件上衣打八折后的利润为 n (1.6x﹣x)=0.6xn(元);
(2)0.6×120×80+2×120×0.6×20﹣120×20﹣1000=5240(元),
所以该商场在这批上衣买卖中盈利5240元.
故答案为2x,1.6x,06xn.
21.解:(1)第n层有(2n﹣1)个小圆圈;
故答案为:(2n﹣1);
(2)令2n﹣1=65,
解得n=33.
所以这是第33层;
故答案为:33;
(3)1+3+5+…+(2n﹣1)=n2;
故答案为:n2;
(4)(1+3+5+…+153)﹣(1+3+5+…+71)
=()2﹣()2
=772﹣362
=4633.
22.解:小丽的说法正确,理由如下:
∵A=a4﹣3a2b2﹣ab3+5,B=2b4﹣2a2b2+ab3,C=a4﹣5a2b2+2b4﹣2,
∴A+B﹣C=(a4﹣3a2b2﹣ab3+5)+(2b4﹣2a2b2+ab3)﹣(a4﹣5a2b2+2b4﹣2)
=a4﹣3a2b2﹣ab3+5+2b4﹣2a2b2+ab3﹣a4+5a2b2﹣2b4+2
=7,
则结果为常数,与a,b的值无关.
