2021--2022学年人教版九年级数学上册第21章一元二次方程单元作业题(word版含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册第21章一元二次方程单元作业题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 133.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 10:27:38 | ||
图片预览


文档简介
人教版九年级数学(上)单元作业题(一)
(一元二次方程)
一、选择题(每小题3分,共36分)
1.下列方程中,是一元二次方程的是:
A.x2+3x+y=0 B.x2++5=0 C.= D.x+y+1=0
2.把方程y2-8y+5=0的左边配成一个完成平方式得:
A.(y+4)2=11 B.(y-4)2=11 C.(y-4)2=21 D.(y+4)2=21
3.下面是某同学在一次测验中解答的填空题.
(1)若x2=a2,则x=a,(2)方程2x(x-1)=(x-1)的解是x=
(3)方程x2―2x―8=0的两根之和为2,其中答案正确的有:
A.0个 B.1个 C.2个 D.3个
4.某经济开发区今年一月份工业产值达50亿元,第一季度总产值为175亿元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,则可列方程为:
A.50(1+x)2=175 B.50+50(1+x)2=175
C.50(1+x)+50(1+x)2=175 D.50+50(1+x)+50(1+x)2=175
5.一元二次方程x2-x+4=0的根的情况是:
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
6.一个直角三角形的面积是24,两条直角边和为14,则这个三角形斜边的长是:
A.9 B.10 C. D.15
7.已知点P(a2,-5a+2)在直线y=―x―4上,则点P的坐标是:
A.(4,-8) B.(9,-13)
C.(-4,8)或(9,-13) D.(4,-8)或(9,-13)
8.如图,已知P为线段AB上一点,若PA2=PB·AB,AB=1,则PB等于:
A. B. C. D.
二.填空题(每小题3分,共24分)
9.设一元二次方程x2-6x+4=0的两个实数根分别为x1和x2,则x1x2 (x1+x2)= .
10.一元二次方程2x2+x+m=0的一个根是1,则m的值是 .
11.请写出一个根式为x=1,另一个根满足-1<x<1的一元二次方程 .
12.若分式的值为0,则x= .
13.如果关于x的一元二次方程kx2-6x+9=0有两个相等的实数根,那么k的值为 .
14.在一次小型会议上,参加会议的代表每两人握手一次,共握手66次,则参加这次会议的有 人.
15.已知x2+3x+5的值是23,则代数式3x2+9x+12的值为 .
16.有一块长方形铁片,长24cm,宽18cm,在四个角都截去相同的小正方形折起来做成一个无盖盒子,使底面积是原来面积的一半,则盒子的高为 .
三.解答题(共计72分)
17.解下列方程.(每小题4分,共16分)
(1)x2+10x+16=0(配方法); (2)x2-x-1=0(公式法);
(3)3x(x-1)=2(x-1)(因式分解法); (4)(x-1)(x-3)+x(x+1)=23.
18.(8分)已知关于x的一元二次方程x2-(m-1)x+m+2=0.
(1)若方程有两个相等的实数根,求m的值;
(2)如果方程的两个实数根之积等于m2-9m+2,求的值.
19.(本题8分)已知关于x的一元二次方程x2+(4m+1)x+2m-1=0
(1) 求证:不论m为何实数,方程总有两个不相等的实数根;
(2) 若方程的两根为x1、x2且满足,求m的值.
20.(8分)定义新运算:对于任意实数,a、b,都有a b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2 5=2(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求x (﹣4)=6,求x的值;
(2)若3 a的值小于10,请判断方程:2x2﹣bx﹣a=0的根的情况.
21.(7分))菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的单价对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金200元.
试问小华选择哪种方案更优惠,请说明理由.
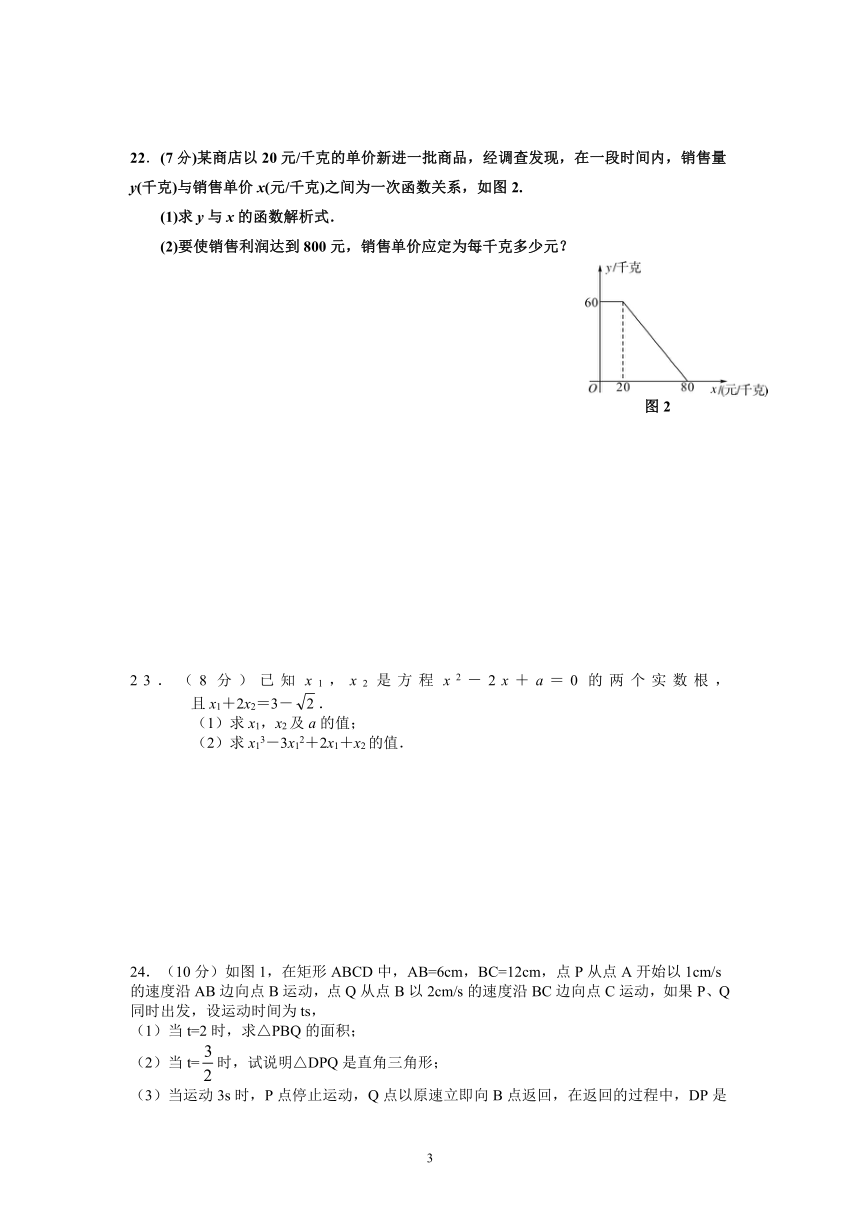
22.(7分)某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图2.
(1)求y与x的函数解析式.
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
图2
23.(8分)已知x1,x2是方程x2-2x+a=0的两个实数根,
且x1+2x2=3-.
(1)求x1,x2及a的值;
(2)求x13-3x12+2x1+x2的值.
24.(10分)如图1,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B运动,点Q从点B以2cm/s的速度沿BC边向点C运动,如果P、Q同时出发,设运动时间为ts,
(1)当t=2时,求△PBQ的面积;
(2)当t=时,试说明△DPQ是直角三角形;
(3)当运动3s时,P点停止运动,Q点以原速立即向B点返回,在返回的过程中,DP是否能平分∠ADQ?若能,求出点Q运动的时间;若不能,请说明理由.
参考答案
一、选择题
1.C 2.B 3.B 4.D 5. C 6.B 7.D 8.A
二、填空题
9.24 10.-3 11.(开放题)如:x2-x=0 12.3
13.1 14.12 15.66 16.3cm
三、解答题
17.(1)x1=-2,x2=-8 (2)x1=,x2=
(3)x1=1,x2= (4)x1=4,x2=―
18.(1)由题意有:(m-1)2-4(m+2)=0
整理得m2―6m―7=0
解得:m1=-1,m2=7
(2)由题意可知:m+2=m2-9m+2
解得:m1=0,m2=10
当m1=0时,(m-1)2-4(m+2)=12-8=-7<0,原方程无实根,故舍去.
∴m=10,当m=10时,==5
19.解:(1)证明:△=(4m+1)2﹣4(2m﹣1)
=16m2+8m+1﹣8m+4=16m2+5>0,
∴不论m为任何实数,方程总有两个不相等的实数根.
(2)∵,即=﹣,
∴由根与系数的关系可得=﹣,解得 m=﹣,
经检验得出m=﹣是原方程的根,即m的值为﹣.
解:(1)∵x (﹣4)=6,
∴x[x﹣(﹣4)]+1=6,
∴x2+4x﹣5=0,
解得:x=1或x=﹣5.
(2)∵3 a<10,
∴3(3﹣a)+1<10
∴10﹣3a<10
∴a>0,
∴△=(﹣b)2+8a=b2+8a>0,
所以该方程有两个不相等的实数根.
21.解:(1)设平均每次下调的百分率为x.由题意,得5(1-x)2=3.2,解这个方程,得x1=0.2,x2=1.8.因为降价的百分率不可能大于1,所以x2=1.8不符合题意,符合题目要求的是x1=0.2=20%.
答:平均每次下调的百分率是20%.
(2)小华选择方案一购买更优惠.
理由:方案一所需费用为3.2×0.9×5 000=14 400(元),
方案二所需费用为3.2×5 000-200×5=15 000(元).
∵14 400元<15 000元,
∴小华选择方案一购买更优惠.
22.(1)y=
(2) 依题意,得
解得:
答:要使销售利润达到800元,销售单价应定为每千克40元或60元.
23.解(1)由题意,得
解得 x1=1+,x2=1-
所以a=x1·x2= (1+) ((1-)=-1.
(2)法一:由题意,得x12-2x1-1=0.
所以x13-3x12+2x1+x2=x13-2x12-x1-x12+3x1+x2=-x12+2x1+1+x1+x2-1=0=2-1=1.
法二:由题意,得x12=2x1+1,
所以x13-3x12+2x1+x2=x1 (2x1+1)-3(2x1+1)+2x1+x2=2x12+x1-6x1-3+2x1+x2
=3(2x1+1)-3x1-3+x2=4x1+2-3x1-3+x2=x1+x2-1=2-1=1.
解:(1)当t=2时,AP=t=2,BQ=2t=4,
∴BP=AB-AP=4,
∴△PBQ的面积=
当t=时,AP=1.5,PB=4.5,BQ=3,CQ=9,
∴DP2=AD2+AP2=2.25+144=146.25,PQ2=PB2+BQ2=29.25,DQ2=CD2+CQ2=117,
∵PQ2+DQ2=DP2,
∴∠DQP=90°,
∴△DPQ是直角三角形.
(3)设存在点Q在BC上,延长DQ与AB延长线交于点F,作PE⊥DF于E,连接PQ.
设QB的长度为x,则QC的长度为(12-x),
若DP能平分∠ADQ,
则PB=PA=PE,易证QE=QB=x
∴DQ=12+x,CQ=12-x
在Rt△CDQ中,DQ2=CD2+CQ2
∴(12+x)2=62+(12-x)2
∵解得x=0.75,
∵点Q的速度为2cm/s,
∴P停止后Q往B走的路程为(6-0.75)=5.25cm.
∴时间为2.625s,加上刚开始的3s,Q点的运动时间为5.625s.
(一元二次方程)
一、选择题(每小题3分,共36分)
1.下列方程中,是一元二次方程的是:
A.x2+3x+y=0 B.x2++5=0 C.= D.x+y+1=0
2.把方程y2-8y+5=0的左边配成一个完成平方式得:
A.(y+4)2=11 B.(y-4)2=11 C.(y-4)2=21 D.(y+4)2=21
3.下面是某同学在一次测验中解答的填空题.
(1)若x2=a2,则x=a,(2)方程2x(x-1)=(x-1)的解是x=
(3)方程x2―2x―8=0的两根之和为2,其中答案正确的有:
A.0个 B.1个 C.2个 D.3个
4.某经济开发区今年一月份工业产值达50亿元,第一季度总产值为175亿元,问二、三月平均每月的增长率是多少?设平均每月的增长率为x,则可列方程为:
A.50(1+x)2=175 B.50+50(1+x)2=175
C.50(1+x)+50(1+x)2=175 D.50+50(1+x)+50(1+x)2=175
5.一元二次方程x2-x+4=0的根的情况是:
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
6.一个直角三角形的面积是24,两条直角边和为14,则这个三角形斜边的长是:
A.9 B.10 C. D.15
7.已知点P(a2,-5a+2)在直线y=―x―4上,则点P的坐标是:
A.(4,-8) B.(9,-13)
C.(-4,8)或(9,-13) D.(4,-8)或(9,-13)
8.如图,已知P为线段AB上一点,若PA2=PB·AB,AB=1,则PB等于:
A. B. C. D.
二.填空题(每小题3分,共24分)
9.设一元二次方程x2-6x+4=0的两个实数根分别为x1和x2,则x1x2 (x1+x2)= .
10.一元二次方程2x2+x+m=0的一个根是1,则m的值是 .
11.请写出一个根式为x=1,另一个根满足-1<x<1的一元二次方程 .
12.若分式的值为0,则x= .
13.如果关于x的一元二次方程kx2-6x+9=0有两个相等的实数根,那么k的值为 .
14.在一次小型会议上,参加会议的代表每两人握手一次,共握手66次,则参加这次会议的有 人.
15.已知x2+3x+5的值是23,则代数式3x2+9x+12的值为 .
16.有一块长方形铁片,长24cm,宽18cm,在四个角都截去相同的小正方形折起来做成一个无盖盒子,使底面积是原来面积的一半,则盒子的高为 .
三.解答题(共计72分)
17.解下列方程.(每小题4分,共16分)
(1)x2+10x+16=0(配方法); (2)x2-x-1=0(公式法);
(3)3x(x-1)=2(x-1)(因式分解法); (4)(x-1)(x-3)+x(x+1)=23.
18.(8分)已知关于x的一元二次方程x2-(m-1)x+m+2=0.
(1)若方程有两个相等的实数根,求m的值;
(2)如果方程的两个实数根之积等于m2-9m+2,求的值.
19.(本题8分)已知关于x的一元二次方程x2+(4m+1)x+2m-1=0
(1) 求证:不论m为何实数,方程总有两个不相等的实数根;
(2) 若方程的两根为x1、x2且满足,求m的值.
20.(8分)定义新运算:对于任意实数,a、b,都有a b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算,比如:2 5=2(2﹣5)+1=2×(﹣3)+1=﹣6+1=﹣5
(1)求x (﹣4)=6,求x的值;
(2)若3 a的值小于10,请判断方程:2x2﹣bx﹣a=0的根的情况.
21.(7分))菜农李伟种植的某蔬菜计划以每千克5元的单价对外批发销售,由于部分菜农盲目扩大种植,造成该蔬菜滞销.李伟为了加快销售,减少损失,对价格经过两次下调后,以每千克3.2元的单价对外批发销售.
(1)求平均每次下调的百分率;
(2)小华准备到李伟处购买5吨该蔬菜,因数量多,李伟决定给予两种优惠方案以供选择:
方案一:打九折销售;
方案二:不打折,每吨优惠现金200元.
试问小华选择哪种方案更优惠,请说明理由.
22.(7分)某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图2.
(1)求y与x的函数解析式.
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
图2
23.(8分)已知x1,x2是方程x2-2x+a=0的两个实数根,
且x1+2x2=3-.
(1)求x1,x2及a的值;
(2)求x13-3x12+2x1+x2的值.
24.(10分)如图1,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B运动,点Q从点B以2cm/s的速度沿BC边向点C运动,如果P、Q同时出发,设运动时间为ts,
(1)当t=2时,求△PBQ的面积;
(2)当t=时,试说明△DPQ是直角三角形;
(3)当运动3s时,P点停止运动,Q点以原速立即向B点返回,在返回的过程中,DP是否能平分∠ADQ?若能,求出点Q运动的时间;若不能,请说明理由.
参考答案
一、选择题
1.C 2.B 3.B 4.D 5. C 6.B 7.D 8.A
二、填空题
9.24 10.-3 11.(开放题)如:x2-x=0 12.3
13.1 14.12 15.66 16.3cm
三、解答题
17.(1)x1=-2,x2=-8 (2)x1=,x2=
(3)x1=1,x2= (4)x1=4,x2=―
18.(1)由题意有:(m-1)2-4(m+2)=0
整理得m2―6m―7=0
解得:m1=-1,m2=7
(2)由题意可知:m+2=m2-9m+2
解得:m1=0,m2=10
当m1=0时,(m-1)2-4(m+2)=12-8=-7<0,原方程无实根,故舍去.
∴m=10,当m=10时,==5
19.解:(1)证明:△=(4m+1)2﹣4(2m﹣1)
=16m2+8m+1﹣8m+4=16m2+5>0,
∴不论m为任何实数,方程总有两个不相等的实数根.
(2)∵,即=﹣,
∴由根与系数的关系可得=﹣,解得 m=﹣,
经检验得出m=﹣是原方程的根,即m的值为﹣.
解:(1)∵x (﹣4)=6,
∴x[x﹣(﹣4)]+1=6,
∴x2+4x﹣5=0,
解得:x=1或x=﹣5.
(2)∵3 a<10,
∴3(3﹣a)+1<10
∴10﹣3a<10
∴a>0,
∴△=(﹣b)2+8a=b2+8a>0,
所以该方程有两个不相等的实数根.
21.解:(1)设平均每次下调的百分率为x.由题意,得5(1-x)2=3.2,解这个方程,得x1=0.2,x2=1.8.因为降价的百分率不可能大于1,所以x2=1.8不符合题意,符合题目要求的是x1=0.2=20%.
答:平均每次下调的百分率是20%.
(2)小华选择方案一购买更优惠.
理由:方案一所需费用为3.2×0.9×5 000=14 400(元),
方案二所需费用为3.2×5 000-200×5=15 000(元).
∵14 400元<15 000元,
∴小华选择方案一购买更优惠.
22.(1)y=
(2) 依题意,得
解得:
答:要使销售利润达到800元,销售单价应定为每千克40元或60元.
23.解(1)由题意,得
解得 x1=1+,x2=1-
所以a=x1·x2= (1+) ((1-)=-1.
(2)法一:由题意,得x12-2x1-1=0.
所以x13-3x12+2x1+x2=x13-2x12-x1-x12+3x1+x2=-x12+2x1+1+x1+x2-1=0=2-1=1.
法二:由题意,得x12=2x1+1,
所以x13-3x12+2x1+x2=x1 (2x1+1)-3(2x1+1)+2x1+x2=2x12+x1-6x1-3+2x1+x2
=3(2x1+1)-3x1-3+x2=4x1+2-3x1-3+x2=x1+x2-1=2-1=1.
解:(1)当t=2时,AP=t=2,BQ=2t=4,
∴BP=AB-AP=4,
∴△PBQ的面积=
当t=时,AP=1.5,PB=4.5,BQ=3,CQ=9,
∴DP2=AD2+AP2=2.25+144=146.25,PQ2=PB2+BQ2=29.25,DQ2=CD2+CQ2=117,
∵PQ2+DQ2=DP2,
∴∠DQP=90°,
∴△DPQ是直角三角形.
(3)设存在点Q在BC上,延长DQ与AB延长线交于点F,作PE⊥DF于E,连接PQ.
设QB的长度为x,则QC的长度为(12-x),
若DP能平分∠ADQ,
则PB=PA=PE,易证QE=QB=x
∴DQ=12+x,CQ=12-x
在Rt△CDQ中,DQ2=CD2+CQ2
∴(12+x)2=62+(12-x)2
∵解得x=0.75,
∵点Q的速度为2cm/s,
∴P停止后Q往B走的路程为(6-0.75)=5.25cm.
∴时间为2.625s,加上刚开始的3s,Q点的运动时间为5.625s.
同课章节目录
