2021-2022学年湘教版七年级数学上册第四章 图形的认识 同步测试 (word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版七年级数学上册第四章 图形的认识 同步测试 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 288.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 10:56:12 | ||
图片预览


文档简介
第四章图形的认识同步测试卷 2021-2022学年湘教版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
在长方体、正方形、球、角、四棱锥、直线、圆锥中,平面图形的个数是( )
A. B. C. D.
下列说法中,错误的是( )
A. 经过一点可以画无数条直线
B. 经过两点的直线有且只有一条
C. 连接两点的线段叫做两点间的距离
D. 线段和线段是同一条线段
如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
A. 过一点有无数条直线
B. 两点之间线段的长度,叫做这两点之间的距离
C. 经过两点有且只有一条直线
D. 两点之间,线段最短
如图,下列表示角的方法错误的是( )
A. 与表示同一个角
B. 表示的是
C. 图中共有三个角:,,
D. 也可用来表示
若1=,2=,则1与2的关系是( )
A. B. C. D. 以上都不对
如图,线段AB=8 cm,C是AB的中点,D是BC的中点,则线段AD长是( )
A. B. C. D.
经过任意三点中的两点可以画出直线( )
A. 条或条 B. 条 C. 条 D. 条
如图,AB是一条直线,O为直线AB上的一点,OD,OE分别平分BOC和AOC,则图中互余的角共有( )
A. 对 B. 对
C. 对 D. 对
如图是某一立方体的侧面展开图,则该立方体是( )
A. B.
C. D.
已知射线OA,由点O引射线OB,OC,AOB=,BOC=,则AOC的度数是( )
A. B. C. 或 D. 或
二、填空题(本大题共8小题,共24分)
如图,点O在直线AB上,AOC=.则BOC的度数是 .
如图,点C,D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是 .
一个角的补角与它的余角的3倍的差是,则这个角为 .
如图所示,将两个三角尺的直角顶点重合.若AOD=,则COB= .
如图,钟表8时30分时,时针与分针所成的锐角的度数为 .
如图,OC是AOB的平分线,如果AOB=,BOD=,那么COD= .
在直线上任取一点A,截取AB=16 cm,再截取AC=40 cm,则AB的中点D与AC的中点E之间的距离为 cm.
把线段AB延长到C,使BC=AB,再反向延长线段AB到D,使AD=AB.若AB=4,则线段DC的长为 .
三、计算题(本大题共1小题,共6分)
计算:
(1)+;
(2)-+.
四、解答题(本大题共7小题,共60分)
如图,已知线段a,b,c,用圆规和直尺画线段,使它等于a+2b-c.(不写作法,保留作图痕迹)
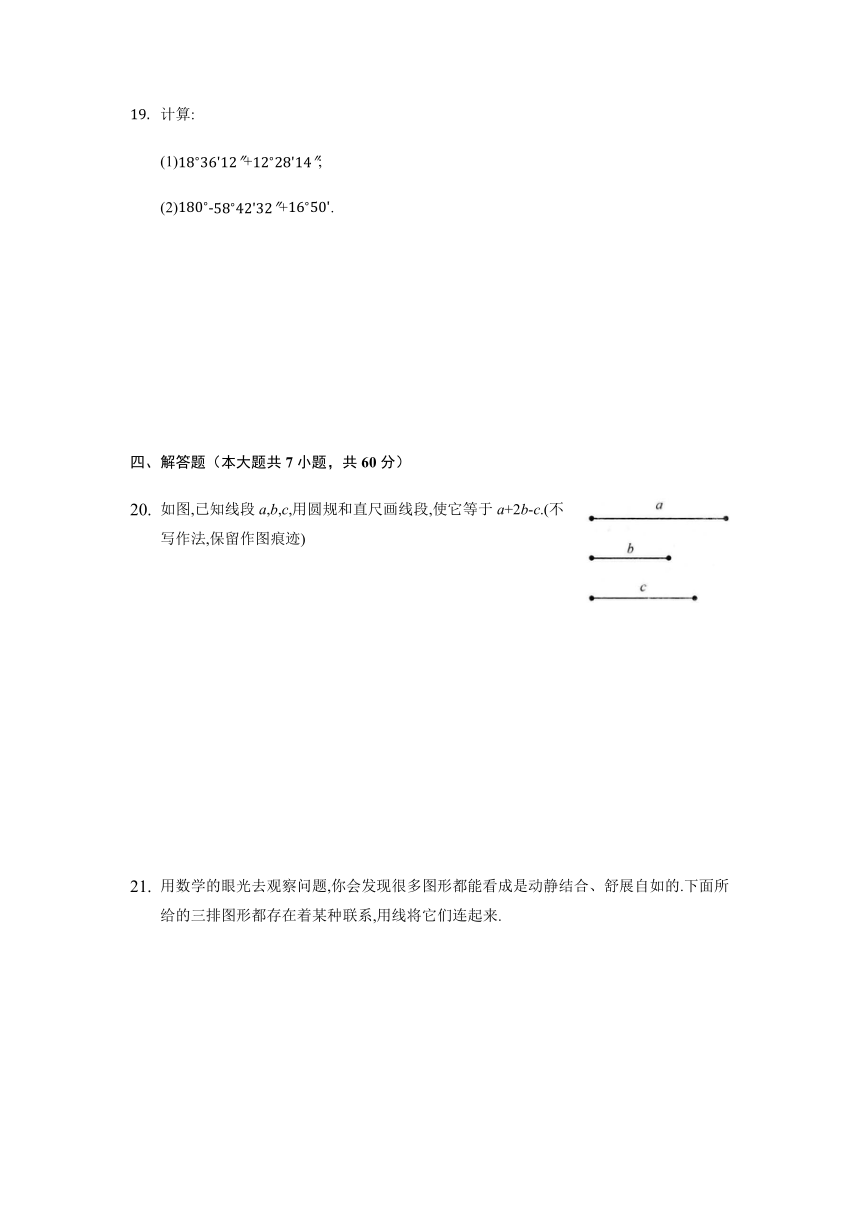
用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合、舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
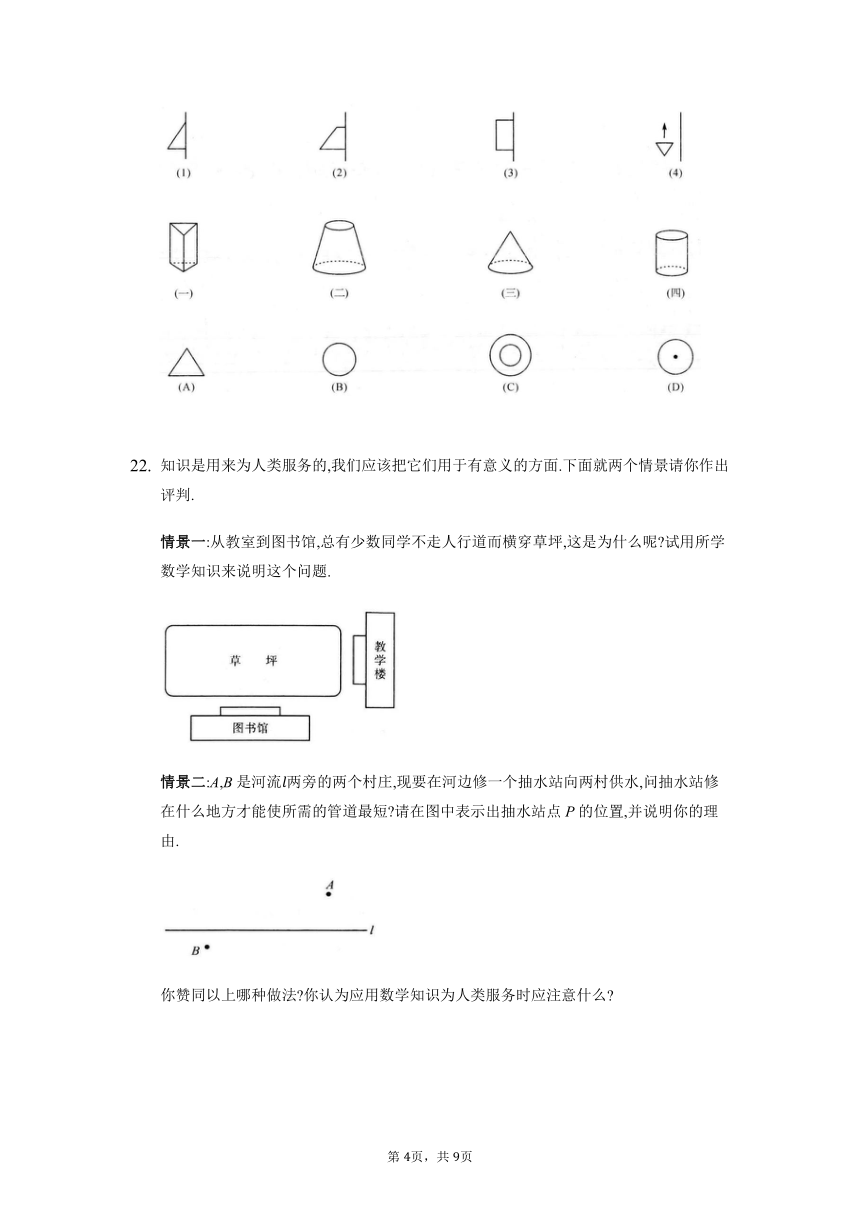
知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢 试用所学数学知识来说明这个问题.
情景二:A,B是河流两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短 请在图中表示出抽水站点P的位置,并说明你的理由.
你赞同以上哪种做法 你认为应用数学知识为人类服务时应注意什么
如图所示,B,C两点把线段AD分成4:5:7三部分,E是线段AD的中点,CD=14 cm,求:
(1)EC的长;
(2)AB:BE的值.
如图,点A,O,B在一条直线上,AOC=,COE=,OD是AOC的平分线.
(1)求AOE和DOE的度数;
(2)OE是COB的平分线吗 为什么
(3)请直接写出COD的余角和补角.
如图,P是线段AB上任一点,AB=12 cm,C,D两点分别从P,B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
(1)若AP=8 cm.
运动1 s后,求CD的长;
当D在线段PB上运动时,试说明AC=2CD;
(2)如果当t=2 s时,CD=1 cm,试探索AP的值.
点O为直线AB上一点,过点O作射线OC,使BOC=,将一直角三角板的直角顶点放在点O处.
(1)如图1,当三角板MON的一边ON与射线OB重合时,则MOC= ;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是MOB的平分线,求旋转角BON和CON的度数;
(3)将三角板MON绕点O逆时针旋转至图3所示的位置时,NOC=AOM,求NOB的度数.
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】41
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】12或28
18.【答案】9
19.【答案】(1)解:原式==.
(2)解:原式=+==.
20.【答案】解:如下图,AB即为所作的线段
21.【答案】解:如图所示:
22.【答案】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短.
情景二:图略.
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法,应用数学知识为人类服务时应注意应用数学不能以破坏环境为代价.
23.【答案】解:设线段AB,BC,CD分别为4x cm,5x cm,7x cm.
因为CD=7x=14,所以x=2.
(1)因为AB=4x=8 cm,BC=5x=10 cm,
所以AD=AB+BC+CD=8+10+14=32(cm).
故EC=AD-CD=32-14=2(cm).
(2)因为BC=10 cm,EC=2 cm,
所以BE=BC-EC=10-2=8(cm).
又因为AB=8 cm,所以AB:BE=8:8=1.
24.【答案】解:(1)因为AOC=,COE=,
所以AOE=AOC+COE=+=.
因为OD是AOC的平分线,
所以COD=AOC==.
所以DOE=COD+COE=+=.
(2)OE是COB的平分线.
理由:因为BOE=-AOE=-=,
所以BOE=COE.
所以OE是COB的平分线.
(3)COD的余角为COE和BOE,补角为BOD.
25.【答案】解:(1)]
由题意可知:CP=21=2(cm),DB=31=3(cm).
因为AP=8 cm,AB=12 cm,
所以PB=AB-AP=4 cm.
所以CD=CP+PB-DB=2+4-3=3(cm).
因为AP=8 cm,AB=12 cm,
所以BP=4 cm,AC=8-2t.
所以DP=4-3t.
所以CD=DP+CP=2t+4-3t=4-t.
所以AC=2CD.
(2)当t=2s时,CP=22=4(cm),DB=32=6(cm),
当点D在C的右边时,如图所示:
由于CD=1 cm,所以CB=CD+DB=7 cm,
所以AC=AB-CB=5 cm,
所以AP=AC+CP=9 cm.
当点D在C的左边时,如图所示:
所以AD=AB-DB=6 cm.
所以AP=AD+CD+CP=11 cm.
综上所述.AP=9 cm或11 cm.
26.【答案】解:(1)
(2)因为BOC=,OC是MOB的平分线,
所以MOB=2BOC=.
所以BON=MOB-MON=-=,
CON=COB-BON=-=.
即BON=,CON=.
(3)因为NOC=AOM,
所以AOM=4NOC.
因为BOC=,
所以AOC=-BOC=-65=.
因为MON=,
所以AOM+NOC=AOC-MON=-=.
即4NOC+NOC=5NOC=,
所以NOC=.
所以NOB=NOC+BOC=+=.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
在长方体、正方形、球、角、四棱锥、直线、圆锥中,平面图形的个数是( )
A. B. C. D.
下列说法中,错误的是( )
A. 经过一点可以画无数条直线
B. 经过两点的直线有且只有一条
C. 连接两点的线段叫做两点间的距离
D. 线段和线段是同一条线段
如图,小亮为将一个衣架固定在墙上,他在衣架两端各用一个钉子进行固定,用数学知识解释他这样操作的原因,应该是( )
A. 过一点有无数条直线
B. 两点之间线段的长度,叫做这两点之间的距离
C. 经过两点有且只有一条直线
D. 两点之间,线段最短
如图,下列表示角的方法错误的是( )
A. 与表示同一个角
B. 表示的是
C. 图中共有三个角:,,
D. 也可用来表示
若1=,2=,则1与2的关系是( )
A. B. C. D. 以上都不对
如图,线段AB=8 cm,C是AB的中点,D是BC的中点,则线段AD长是( )
A. B. C. D.
经过任意三点中的两点可以画出直线( )
A. 条或条 B. 条 C. 条 D. 条
如图,AB是一条直线,O为直线AB上的一点,OD,OE分别平分BOC和AOC,则图中互余的角共有( )
A. 对 B. 对
C. 对 D. 对
如图是某一立方体的侧面展开图,则该立方体是( )
A. B.
C. D.
已知射线OA,由点O引射线OB,OC,AOB=,BOC=,则AOC的度数是( )
A. B. C. 或 D. 或
二、填空题(本大题共8小题,共24分)
如图,点O在直线AB上,AOC=.则BOC的度数是 .
如图,点C,D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是 .
一个角的补角与它的余角的3倍的差是,则这个角为 .
如图所示,将两个三角尺的直角顶点重合.若AOD=,则COB= .
如图,钟表8时30分时,时针与分针所成的锐角的度数为 .
如图,OC是AOB的平分线,如果AOB=,BOD=,那么COD= .
在直线上任取一点A,截取AB=16 cm,再截取AC=40 cm,则AB的中点D与AC的中点E之间的距离为 cm.
把线段AB延长到C,使BC=AB,再反向延长线段AB到D,使AD=AB.若AB=4,则线段DC的长为 .
三、计算题(本大题共1小题,共6分)
计算:
(1)+;
(2)-+.
四、解答题(本大题共7小题,共60分)
如图,已知线段a,b,c,用圆规和直尺画线段,使它等于a+2b-c.(不写作法,保留作图痕迹)
用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合、舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢 试用所学数学知识来说明这个问题.
情景二:A,B是河流两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短 请在图中表示出抽水站点P的位置,并说明你的理由.
你赞同以上哪种做法 你认为应用数学知识为人类服务时应注意什么
如图所示,B,C两点把线段AD分成4:5:7三部分,E是线段AD的中点,CD=14 cm,求:
(1)EC的长;
(2)AB:BE的值.
如图,点A,O,B在一条直线上,AOC=,COE=,OD是AOC的平分线.
(1)求AOE和DOE的度数;
(2)OE是COB的平分线吗 为什么
(3)请直接写出COD的余角和补角.
如图,P是线段AB上任一点,AB=12 cm,C,D两点分别从P,B同时向A点运动,且C点的运动速度为2 cm/s,D点的运动速度为3 cm/s,运动的时间为t s.
(1)若AP=8 cm.
运动1 s后,求CD的长;
当D在线段PB上运动时,试说明AC=2CD;
(2)如果当t=2 s时,CD=1 cm,试探索AP的值.
点O为直线AB上一点,过点O作射线OC,使BOC=,将一直角三角板的直角顶点放在点O处.
(1)如图1,当三角板MON的一边ON与射线OB重合时,则MOC= ;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是MOB的平分线,求旋转角BON和CON的度数;
(3)将三角板MON绕点O逆时针旋转至图3所示的位置时,NOC=AOM,求NOB的度数.
1.【答案】A
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】D
10.【答案】D
11.【答案】
12.【答案】41
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】12或28
18.【答案】9
19.【答案】(1)解:原式==.
(2)解:原式=+==.
20.【答案】解:如下图,AB即为所作的线段
21.【答案】解:如图所示:
22.【答案】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短.
情景二:图略.
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法,应用数学知识为人类服务时应注意应用数学不能以破坏环境为代价.
23.【答案】解:设线段AB,BC,CD分别为4x cm,5x cm,7x cm.
因为CD=7x=14,所以x=2.
(1)因为AB=4x=8 cm,BC=5x=10 cm,
所以AD=AB+BC+CD=8+10+14=32(cm).
故EC=AD-CD=32-14=2(cm).
(2)因为BC=10 cm,EC=2 cm,
所以BE=BC-EC=10-2=8(cm).
又因为AB=8 cm,所以AB:BE=8:8=1.
24.【答案】解:(1)因为AOC=,COE=,
所以AOE=AOC+COE=+=.
因为OD是AOC的平分线,
所以COD=AOC==.
所以DOE=COD+COE=+=.
(2)OE是COB的平分线.
理由:因为BOE=-AOE=-=,
所以BOE=COE.
所以OE是COB的平分线.
(3)COD的余角为COE和BOE,补角为BOD.
25.【答案】解:(1)]
由题意可知:CP=21=2(cm),DB=31=3(cm).
因为AP=8 cm,AB=12 cm,
所以PB=AB-AP=4 cm.
所以CD=CP+PB-DB=2+4-3=3(cm).
因为AP=8 cm,AB=12 cm,
所以BP=4 cm,AC=8-2t.
所以DP=4-3t.
所以CD=DP+CP=2t+4-3t=4-t.
所以AC=2CD.
(2)当t=2s时,CP=22=4(cm),DB=32=6(cm),
当点D在C的右边时,如图所示:
由于CD=1 cm,所以CB=CD+DB=7 cm,
所以AC=AB-CB=5 cm,
所以AP=AC+CP=9 cm.
当点D在C的左边时,如图所示:
所以AD=AB-DB=6 cm.
所以AP=AD+CD+CP=11 cm.
综上所述.AP=9 cm或11 cm.
26.【答案】解:(1)
(2)因为BOC=,OC是MOB的平分线,
所以MOB=2BOC=.
所以BON=MOB-MON=-=,
CON=COB-BON=-=.
即BON=,CON=.
(3)因为NOC=AOM,
所以AOM=4NOC.
因为BOC=,
所以AOC=-BOC=-65=.
因为MON=,
所以AOM+NOC=AOC-MON=-=.
即4NOC+NOC=5NOC=,
所以NOC=.
所以NOB=NOC+BOC=+=.
第2页,共2页
同课章节目录
