4.5函数的应用(二)能力提升练习-2021-2022学年高一数学上学期人教A版(2019)必修第一册(含答案)
文档属性
| 名称 | 4.5函数的应用(二)能力提升练习-2021-2022学年高一数学上学期人教A版(2019)必修第一册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 104.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 15:04:43 | ||
图片预览

文档简介
4.5函数的应用(二)——能力提升
(共24题)
一、选择题(共14题)
函数 的零点是
A. B. C. D.
若函数 的一个零点在区间 内,则实数 的取值范围是
A. B. C. D.
函数 的零点是
A. B. C. D.
用二分法研究函数 的零点时,第一次经过计算得 ,,则其中一个零点所在的区间和第二次应计算的函数值分别为
A. , B. ,
C. , D. ,
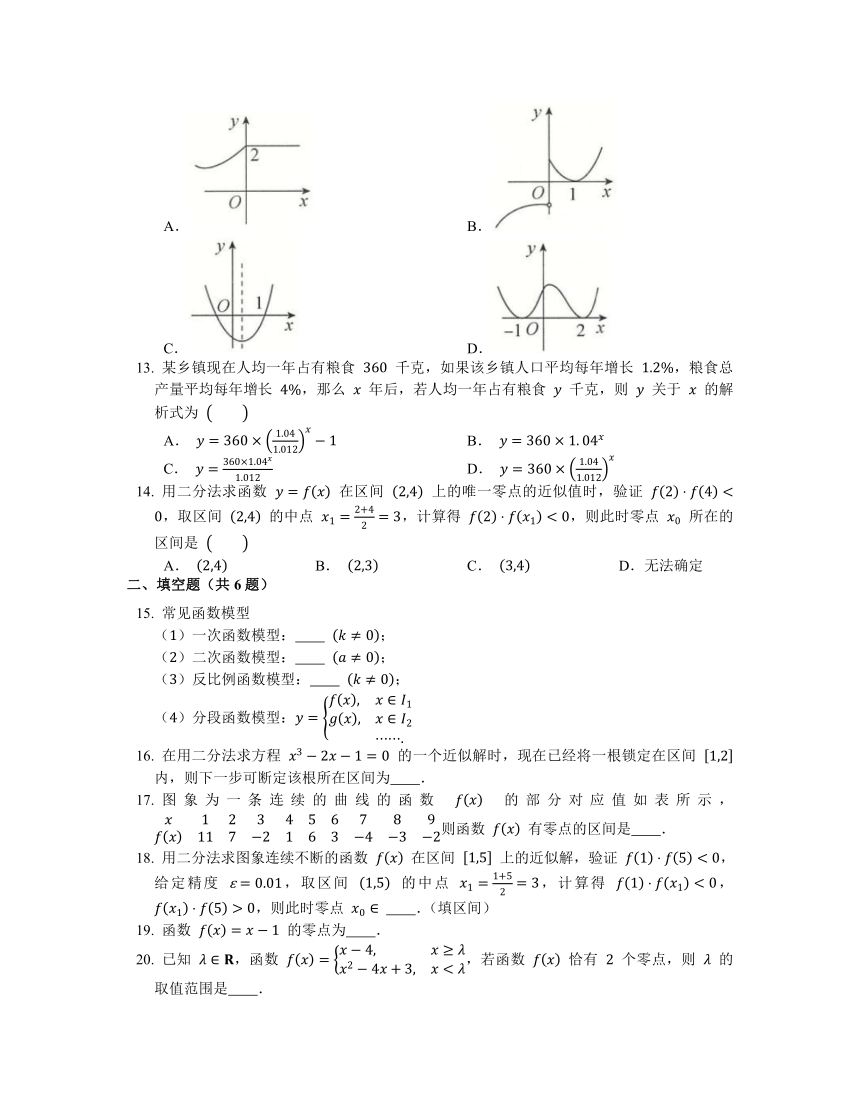
下列图象表示的函数中能用二分法求零点的是
A. B. C. D.
函数 的零点所在的大致区间的
A. B. C. D.
函数 的零点所在区间是
A. B. C. D.
已知 在区间 内有一个零点 ,若用二分法求 的近似值(精确度为 ),则最少需要将区间等分的次数为
A. B. C. D.
设 是实数,关于 的方程 的根的情况是
A.有两个不相等的实根 B.有两个相等的实根
C.没有实根 D.与实数 的具体取值有关
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前 天监测到的数据:则下列函数模型中,能较好地反映计算机在第 天被感染的数量 与 之间的关系的是
A. B.
C. D.
函数 的零点的个数是
A. B. C. D.
下列图象表示的函数中没有零点的是
A. B.
C. D.
某乡镇现在人均一年占有粮食 千克,如果该乡镇人口平均每年增长 ,粮食总产量平均每年增长 ,那么 年后,若人均一年占有粮食 千克,则 关于 的解析式为
A. B.
C. D.
用二分法求函数 在区间 上的唯一零点的近似值时,验证 ,取区间 的中点 ,计算得 ,则此时零点 所在的区间是
A. B. C. D.无法确定
二、填空题(共6题)
常见函数模型
()一次函数模型: ;
()二次函数模型: ;
()反比例函数模型: ;
()分段函数模型:
在用二分法求方程 的一个近似解时,现在已经将一根锁定在区间 内,则下一步可断定该根所在区间为 .
图象为一条连续的曲线的函数 的部分对应值如表所示,则函数 有零点的区间是 .
用二分法求图象连续不断的函数 在区间 上的近似解,验证 ,给定精度 ,取区间 的中点 ,计算得 ,,则此时零点 .(填区间)
函数 的零点为 .
已知 ,函数 ,若函数 恰有 个零点,则 的取值范围是 .
三、解答题(共4题)
已知函数 ,求满足下列条件时 的取值范围.
(1) 函数 没有零点;
(2) 函数 有两个零点;
(3) 函数 有三个零点;
(4) 函数 有四个零点.
用二分法求方程的近似解
()二分法:对于区间 上连续不断且 的函数 ,通过每次把 的零点所在的区间收缩一半的方法,使区间的两个端点逐步逼近函数的零点,以求得零点的近似值的方法叫做二分法.
()用二分法求函数零点的近似值的步骤:
①确定区间 ,验证 ,给定精确度 ;
②求区间 的中点 ,
a.若 ,则 就是函数的零点;
b.若 ,则令 (此时零点 );
c.若 ,则令 (此时零点 );
d.判断是否达到精确度 .
若 ,则得到零点的近似值 (或 ),否则重复 ,直到达到精确度要求为止.
二分法能求所有的零点吗?
某厂生产某种产品 (百台),总成本为 (万元),其中固定成本为 万元,每生产 百台成本增加 万元,销售收入为 (万元).且 与 之间的函数关系式为:.
假定该产品产销平衡.
(1) 该厂若要不亏本,产量 应控制在什么范围内?
(2) 生产多少台时,可使利润最大?
(3) 求利润最大时产品的售价(保留三位有效数字).
根据函数 在 上的图象,确定方程 的根的个数.
答案
一、选择题(共14题)
1. B
2. C
3. B
4. D
5. C
6. B
7. C
8. A
9. B
10. D
11. A
12. A
13. D
14. B
二、填空题(共6题)
15. ; ;
16.
17. ,,
18.
19.
20.
三、解答题(共4题)
21.
(1) 设 ,,作出它们的图象,如图所示.
函数 没有零点,即直线 与 的图象没有交点,观察图象可知,此时 .
(2) 函数 有两个零点,即直线 与 的图象有两个交点,观察图象可知,此时 或 .
(3) 函数 有三个零点,即直线 与 的图象有三个交点,观察图象可知,此时 .
(4) 函数 有四个零点,即直线 与 的图象有四个交点,观察图象可知,此时 .
22. 二分法只能求变号零点,也就是零点邻近的左右两边的函数值正负相反;
不能求零点附近左右两侧函数值的符号相同的零点.
23.
(1) 由题意,成本函数为 ,
设利润为 (万元),
则利润函数为
要不亏本,即要 ,分段解不等式 ,得 .
故要不亏本,产量 应控制在 的范围内.
(2) 当 时,从二次函数 的性质可知:
当 时,函数取得最大值 ;
当 时,.
所以取 ,即生产 台时,可使利润最大.
(3) 由()知当 时,利润最大,设售价为 .
此时的售价 (万元/百台),
即利润最大时售价为 元/台.
24. 方程 的根即为函数 的图象与 轴交点的横坐标,由图可知,方程有 个根,即 ,,.
(共24题)
一、选择题(共14题)
函数 的零点是
A. B. C. D.
若函数 的一个零点在区间 内,则实数 的取值范围是
A. B. C. D.
函数 的零点是
A. B. C. D.
用二分法研究函数 的零点时,第一次经过计算得 ,,则其中一个零点所在的区间和第二次应计算的函数值分别为
A. , B. ,
C. , D. ,
下列图象表示的函数中能用二分法求零点的是
A. B. C. D.
函数 的零点所在的大致区间的
A. B. C. D.
函数 的零点所在区间是
A. B. C. D.
已知 在区间 内有一个零点 ,若用二分法求 的近似值(精确度为 ),则最少需要将区间等分的次数为
A. B. C. D.
设 是实数,关于 的方程 的根的情况是
A.有两个不相等的实根 B.有两个相等的实根
C.没有实根 D.与实数 的具体取值有关
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前 天监测到的数据:则下列函数模型中,能较好地反映计算机在第 天被感染的数量 与 之间的关系的是
A. B.
C. D.
函数 的零点的个数是
A. B. C. D.
下列图象表示的函数中没有零点的是
A. B.
C. D.
某乡镇现在人均一年占有粮食 千克,如果该乡镇人口平均每年增长 ,粮食总产量平均每年增长 ,那么 年后,若人均一年占有粮食 千克,则 关于 的解析式为
A. B.
C. D.
用二分法求函数 在区间 上的唯一零点的近似值时,验证 ,取区间 的中点 ,计算得 ,则此时零点 所在的区间是
A. B. C. D.无法确定
二、填空题(共6题)
常见函数模型
()一次函数模型: ;
()二次函数模型: ;
()反比例函数模型: ;
()分段函数模型:
在用二分法求方程 的一个近似解时,现在已经将一根锁定在区间 内,则下一步可断定该根所在区间为 .
图象为一条连续的曲线的函数 的部分对应值如表所示,则函数 有零点的区间是 .
用二分法求图象连续不断的函数 在区间 上的近似解,验证 ,给定精度 ,取区间 的中点 ,计算得 ,,则此时零点 .(填区间)
函数 的零点为 .
已知 ,函数 ,若函数 恰有 个零点,则 的取值范围是 .
三、解答题(共4题)
已知函数 ,求满足下列条件时 的取值范围.
(1) 函数 没有零点;
(2) 函数 有两个零点;
(3) 函数 有三个零点;
(4) 函数 有四个零点.
用二分法求方程的近似解
()二分法:对于区间 上连续不断且 的函数 ,通过每次把 的零点所在的区间收缩一半的方法,使区间的两个端点逐步逼近函数的零点,以求得零点的近似值的方法叫做二分法.
()用二分法求函数零点的近似值的步骤:
①确定区间 ,验证 ,给定精确度 ;
②求区间 的中点 ,
a.若 ,则 就是函数的零点;
b.若 ,则令 (此时零点 );
c.若 ,则令 (此时零点 );
d.判断是否达到精确度 .
若 ,则得到零点的近似值 (或 ),否则重复 ,直到达到精确度要求为止.
二分法能求所有的零点吗?
某厂生产某种产品 (百台),总成本为 (万元),其中固定成本为 万元,每生产 百台成本增加 万元,销售收入为 (万元).且 与 之间的函数关系式为:.
假定该产品产销平衡.
(1) 该厂若要不亏本,产量 应控制在什么范围内?
(2) 生产多少台时,可使利润最大?
(3) 求利润最大时产品的售价(保留三位有效数字).
根据函数 在 上的图象,确定方程 的根的个数.
答案
一、选择题(共14题)
1. B
2. C
3. B
4. D
5. C
6. B
7. C
8. A
9. B
10. D
11. A
12. A
13. D
14. B
二、填空题(共6题)
15. ; ;
16.
17. ,,
18.
19.
20.
三、解答题(共4题)
21.
(1) 设 ,,作出它们的图象,如图所示.
函数 没有零点,即直线 与 的图象没有交点,观察图象可知,此时 .
(2) 函数 有两个零点,即直线 与 的图象有两个交点,观察图象可知,此时 或 .
(3) 函数 有三个零点,即直线 与 的图象有三个交点,观察图象可知,此时 .
(4) 函数 有四个零点,即直线 与 的图象有四个交点,观察图象可知,此时 .
22. 二分法只能求变号零点,也就是零点邻近的左右两边的函数值正负相反;
不能求零点附近左右两侧函数值的符号相同的零点.
23.
(1) 由题意,成本函数为 ,
设利润为 (万元),
则利润函数为
要不亏本,即要 ,分段解不等式 ,得 .
故要不亏本,产量 应控制在 的范围内.
(2) 当 时,从二次函数 的性质可知:
当 时,函数取得最大值 ;
当 时,.
所以取 ,即生产 台时,可使利润最大.
(3) 由()知当 时,利润最大,设售价为 .
此时的售价 (万元/百台),
即利润最大时售价为 元/台.
24. 方程 的根即为函数 的图象与 轴交点的横坐标,由图可知,方程有 个根,即 ,,.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
