3.6.2 圆的切线判定和三角形的内切圆 课件(共22张PPT)
文档属性
| 名称 | 3.6.2 圆的切线判定和三角形的内切圆 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
北师版九年级下册 圆
§3.6.2 切线的判定与三角形的内切圆
1.通过学习判定一条直线是否为圆的切线的4类方法,训练学生的推理能力;
2.会过圆上一点画圆的切线,训练学生的作图能力;
3.会作三角形的内切圆,掌握运用相关概念解题的方法.
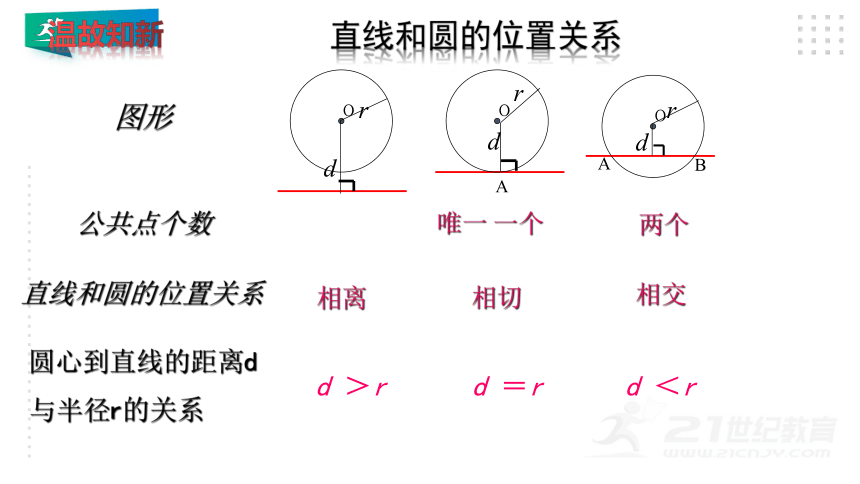
直线和圆的位置关系
图形
公共点个数
直线和圆的位置关系
圆心到直线的距离d与半径r的关系
唯一 一个
两个
相离
相切
相交
d <r
d =r
d >r
O
O
O
d
r
d
r
d
r
A
A
B
温故知新
O
d
r
B
C
A
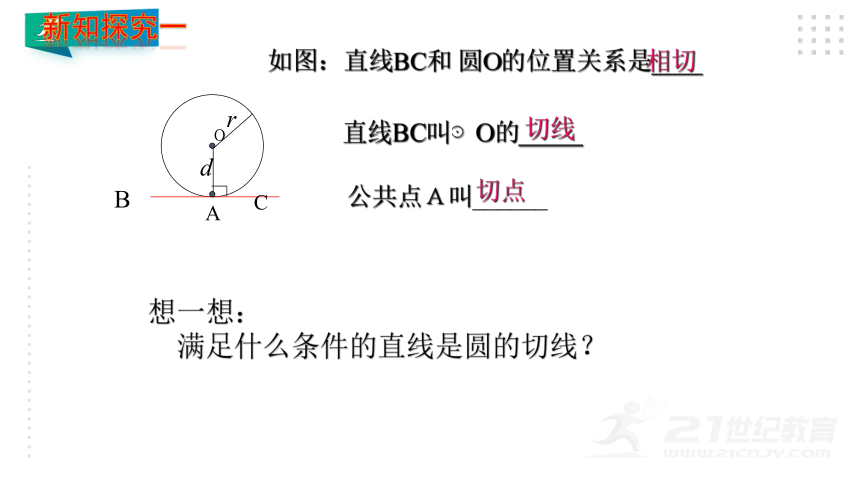
如图:直线BC和 圆O的位置关系是____
切线
切点
公共点A叫______
想一想:
满足什么条件的直线是圆的切线?
直线BC叫⊙O的_____
相切
新知探究一
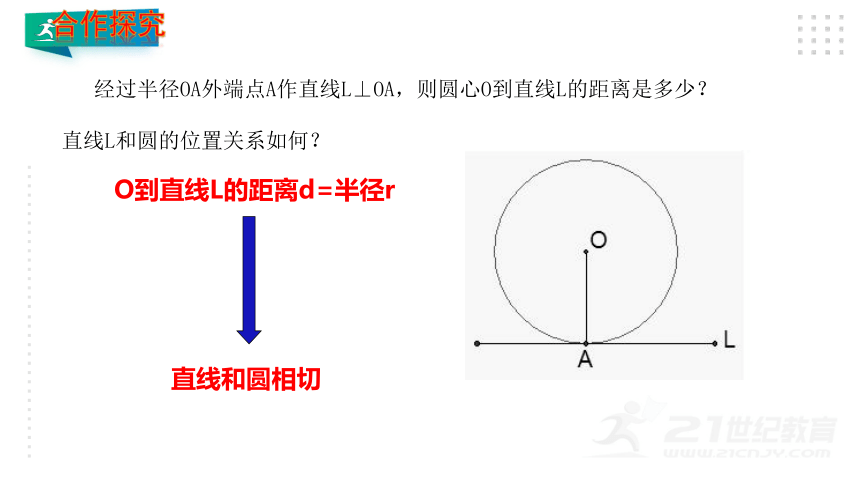
经过半径OA外端点A作直线L⊥OA,则圆心O到直线L的距离是多少?
直线L和圆的位置关系如何?
O到直线L的距离d=半径r
直线和圆相切
合作探究
O
A
B
C
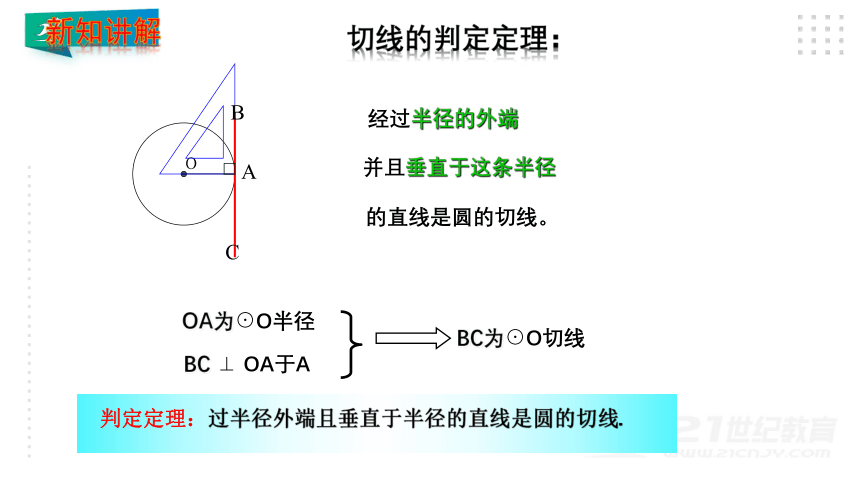
经过半径的外端
并且垂直于这条半径
的直线是圆的切线。
切线的判定定理:
OA为⊙O半径
BC ⊥ OA于A
BC为⊙O切线
新知讲解
判定定理:过半径外端且垂直于半径的直线是圆的切线.
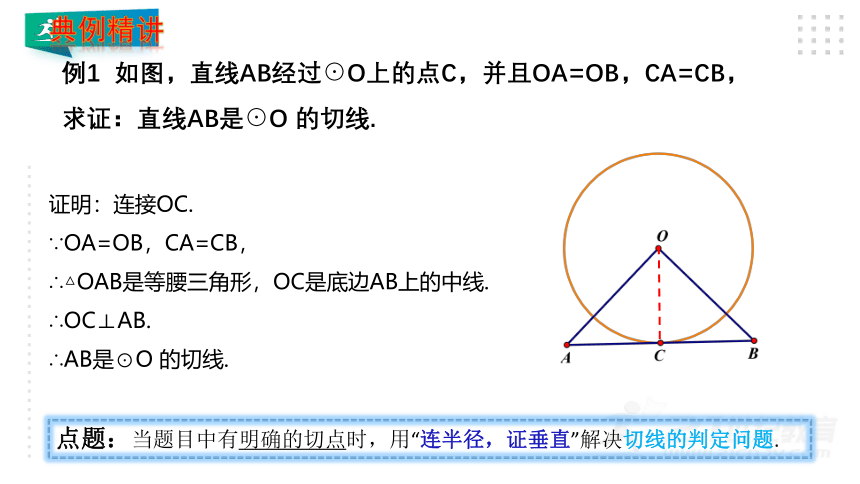
例1 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O 的切线.
证明:连接OC.
∵OA=OB,CA=CB,
∴△OAB是等腰三角形,OC是底边AB上的中线.
∴OC⊥AB.
∴AB是⊙O 的切线.
典例精讲
点题:当题目中有明确的切点时,用“连半径,证垂直”解决切线的判定问题.
圆的切线判定的三种方法
1、利用定义:与圆有唯一公共点的直线是圆的切线。
2、利用d=r:即到圆心的距离d等于圆的半径r的直线是圆的切线。
3、利用切线的判定定理:经过半径的外端并且垂直于这条半径的
直线是圆的切线。
归纳总结一
简称:“连半径,证垂直”
O
A
B
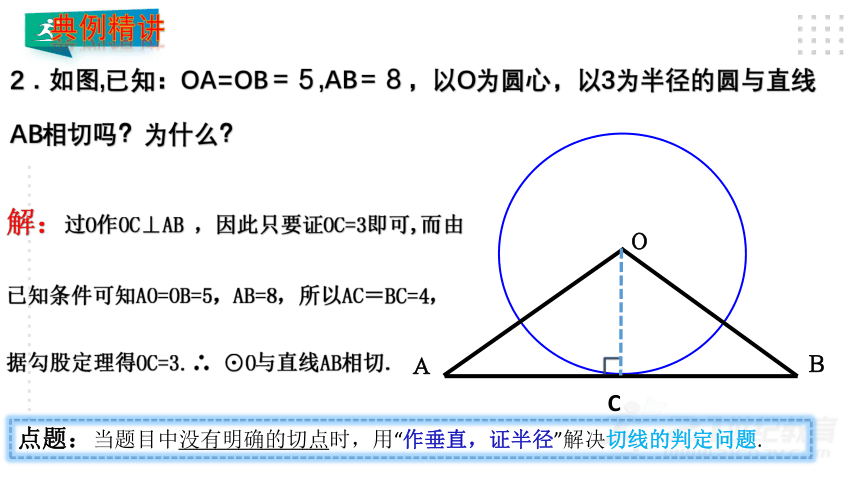
2.如图,已知:OA=OB=5,AB=8,以O为圆心,以3为半径的圆与直线AB相切吗?为什么?
典例精讲
∟
C
解:过O作OC⊥AB ,因此只要证OC=3即可,而由已知条件可知AO=OB=5,AB=8,所以AC=BC=4,据勾股定理得OC=3.∴ ⊙O与直线AB相切.
点题:当题目中没有明确的切点时,用“作垂直,证半径”解决切线的判定问题.
如图,在△ABC中,作一个圆使它与这个三角形的三边都相切.
A
B
C
新知探究二
三角形的内切圆作法:
(1)作∠ABC,∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.
A
B
C
I●
┓
●
D
M
N
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
归纳总结二
A
B
C
I●
┓
●
E
F
还记得前几节讲过的“外心“?
外心:三角形外接圆的圆心.它是三边垂直平分线的交点.
如图,已知△ABC中,I是△ABC的内心,
(1)若∠A=68°,则∠BIC= .
(2)若∠A=80°,则∠BIC= .
(3)若∠BOC=110°,则∠A= .
跟踪练习
.
124°
130°
40°
分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明它们内心的位置情况.
内心均在三角形内部
做一做
跟踪练习
判断题:
1.三角形的内心到三角形各个顶点的距离相等( )
2.三角形的外心到三角形各边的距离相等 ( )
3.等边三角形的内心和外心重合( )
4.三角形的内心一定在三角形的内部( )
错
错
对
对
2.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为( )
A.40° B.50° C.80° D.100°
C
跟踪练习
1.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°, AC=3,BC=4.求⊙O的半径r .
能力拓展训练
解:由Rt△ABC的三边长与其内切圆半径间的关系得:
此公式的推导可作为一个思考题,老师择机引导学生思考证明一下.
2、如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.求证:CD是⊙O的切线.
证明:连接OC,∵AC=CD,∠D=30°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠ACO=∠A=30°.
∴∠COD=60°.
∴∠OCD=90°,即OC⊥CD.
∴CD是⊙O的切线.
能力拓展训练
3、如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,AE⊥CP于点D,如果AC平分∠DAB.求证:直线CP与⊙O相切.
证明:连接OC.
∵OA=OC,∴∠OCA=∠OAC.
∵AC平分∠DAB,∴∠DAC=∠OAC.∴∠DAC=∠OCA.∴OC∥AD.
又∵AD⊥CP,
∴OC⊥CP.
∴直线CP与⊙O相切.
能力拓展训练
4.(2020·河南模拟)如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
求证:(1)∠PAC=∠CAB;
(2)AC2=AP·AB.
证明:(1)连接OC.
∵直线PC切半圆O于点C,∴OC⊥PC.
∵AP⊥PC,
∴OC∥AP.
∴∠PAC=∠OCA.
∵OC=OA,
∴∠CAB=∠OCA.
∴∠PAC=∠CAB.
.
(2)∵AB为半圆O的直径,∴∠ACB=90°.
∵AP⊥PC,∴∠P=∠ACB=90°.
由(1)可知∠PAC=∠CAB,
∴△PAC∽△CAB.
∴AB(AC)=AC(AP),即AC2=AP·AB
能力拓展训练
5.如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB= BC;④BD=CD,
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
B
能力拓展训练
判定方法 根据
方法1 和圆有唯一公共点的直线是圆的切线 切线定义
方法2 和圆心距离d等于圆的半径r的直线是圆的切线 d=r
方法3 过半径外端且和半径垂直的直线是圆的切线 切线判定定理
一、要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:
二、两个口诀:1、“连半径,证垂直”(有切点);2、“作垂直,证半径”(无切点)
三、了解三角形的内切圆、三角形的内心的概念与外接圆、外心的区别.
北师版九年级下册 圆
§3.6.2 切线的判定与三角形的内切圆
1.通过学习判定一条直线是否为圆的切线的4类方法,训练学生的推理能力;
2.会过圆上一点画圆的切线,训练学生的作图能力;
3.会作三角形的内切圆,掌握运用相关概念解题的方法.
直线和圆的位置关系
图形
公共点个数
直线和圆的位置关系
圆心到直线的距离d与半径r的关系
唯一 一个
两个
相离
相切
相交
d <r
d =r
d >r
O
O
O
d
r
d
r
d
r
A
A
B
温故知新
O
d
r
B
C
A
如图:直线BC和 圆O的位置关系是____
切线
切点
公共点A叫______
想一想:
满足什么条件的直线是圆的切线?
直线BC叫⊙O的_____
相切
新知探究一
经过半径OA外端点A作直线L⊥OA,则圆心O到直线L的距离是多少?
直线L和圆的位置关系如何?
O到直线L的距离d=半径r
直线和圆相切
合作探究
O
A
B
C
经过半径的外端
并且垂直于这条半径
的直线是圆的切线。
切线的判定定理:
OA为⊙O半径
BC ⊥ OA于A
BC为⊙O切线
新知讲解
判定定理:过半径外端且垂直于半径的直线是圆的切线.
例1 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O 的切线.
证明:连接OC.
∵OA=OB,CA=CB,
∴△OAB是等腰三角形,OC是底边AB上的中线.
∴OC⊥AB.
∴AB是⊙O 的切线.
典例精讲
点题:当题目中有明确的切点时,用“连半径,证垂直”解决切线的判定问题.
圆的切线判定的三种方法
1、利用定义:与圆有唯一公共点的直线是圆的切线。
2、利用d=r:即到圆心的距离d等于圆的半径r的直线是圆的切线。
3、利用切线的判定定理:经过半径的外端并且垂直于这条半径的
直线是圆的切线。
归纳总结一
简称:“连半径,证垂直”
O
A
B
2.如图,已知:OA=OB=5,AB=8,以O为圆心,以3为半径的圆与直线AB相切吗?为什么?
典例精讲
∟
C
解:过O作OC⊥AB ,因此只要证OC=3即可,而由已知条件可知AO=OB=5,AB=8,所以AC=BC=4,据勾股定理得OC=3.∴ ⊙O与直线AB相切.
点题:当题目中没有明确的切点时,用“作垂直,证半径”解决切线的判定问题.
如图,在△ABC中,作一个圆使它与这个三角形的三边都相切.
A
B
C
新知探究二
三角形的内切圆作法:
(1)作∠ABC,∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求的圆.
A
B
C
I●
┓
●
D
M
N
定义:与三角形三边都相切的圆叫做三角形的内切圆. 内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点.
归纳总结二
A
B
C
I●
┓
●
E
F
还记得前几节讲过的“外心“?
外心:三角形外接圆的圆心.它是三边垂直平分线的交点.
如图,已知△ABC中,I是△ABC的内心,
(1)若∠A=68°,则∠BIC= .
(2)若∠A=80°,则∠BIC= .
(3)若∠BOC=110°,则∠A= .
跟踪练习
.
124°
130°
40°
分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明它们内心的位置情况.
内心均在三角形内部
做一做
跟踪练习
判断题:
1.三角形的内心到三角形各个顶点的距离相等( )
2.三角形的外心到三角形各边的距离相等 ( )
3.等边三角形的内心和外心重合( )
4.三角形的内心一定在三角形的内部( )
错
错
对
对
2.如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连结OD.若∠C=50°,则∠AOD的度数为( )
A.40° B.50° C.80° D.100°
C
跟踪练习
1.已知:如图,⊙O是Rt△ABC的内切圆,∠C=90°, AC=3,BC=4.求⊙O的半径r .
能力拓展训练
解:由Rt△ABC的三边长与其内切圆半径间的关系得:
此公式的推导可作为一个思考题,老师择机引导学生思考证明一下.
2、如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.求证:CD是⊙O的切线.
证明:连接OC,∵AC=CD,∠D=30°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠ACO=∠A=30°.
∴∠COD=60°.
∴∠OCD=90°,即OC⊥CD.
∴CD是⊙O的切线.
能力拓展训练
3、如图,AB是⊙O的直径,AC是⊙O的弦,AE交⊙O于点E,AE⊥CP于点D,如果AC平分∠DAB.求证:直线CP与⊙O相切.
证明:连接OC.
∵OA=OC,∴∠OCA=∠OAC.
∵AC平分∠DAB,∴∠DAC=∠OAC.∴∠DAC=∠OCA.∴OC∥AD.
又∵AD⊥CP,
∴OC⊥CP.
∴直线CP与⊙O相切.
能力拓展训练
4.(2020·河南模拟)如图,AB为半圆O的直径,直线PC切半圆O于点C,AP⊥PC,P为垂足.
求证:(1)∠PAC=∠CAB;
(2)AC2=AP·AB.
证明:(1)连接OC.
∵直线PC切半圆O于点C,∴OC⊥PC.
∵AP⊥PC,
∴OC∥AP.
∴∠PAC=∠OCA.
∵OC=OA,
∴∠CAB=∠OCA.
∴∠PAC=∠CAB.
.
(2)∵AB为半圆O的直径,∴∠ACB=90°.
∵AP⊥PC,∴∠P=∠ACB=90°.
由(1)可知∠PAC=∠CAB,
∴△PAC∽△CAB.
∴AB(AC)=AC(AP),即AC2=AP·AB
能力拓展训练
5.如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:①AD=DC;②AB=BD;③AB= BC;④BD=CD,
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
B
能力拓展训练
判定方法 根据
方法1 和圆有唯一公共点的直线是圆的切线 切线定义
方法2 和圆心距离d等于圆的半径r的直线是圆的切线 d=r
方法3 过半径外端且和半径垂直的直线是圆的切线 切线判定定理
一、要判定一条直线是圆的切线,我们已学过三种方法,如下表所示:
二、两个口诀:1、“连半径,证垂直”(有切点);2、“作垂直,证半径”(无切点)
三、了解三角形的内切圆、三角形的内心的概念与外接圆、外心的区别.
