3.6.1 圆的切线 课件(共26张PPT)
文档属性
| 名称 | 3.6.1 圆的切线 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 67.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 09:56:23 | ||
图片预览







文档简介
(共26张PPT)
北师版九年级下册 圆
§3.6.1 直线与圆的位置关系
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离d 与半径r 之间的关系来判定它们.
2.理解并掌握“切线的性质”,能灵活运用“见切点,连半径”口诀解题.
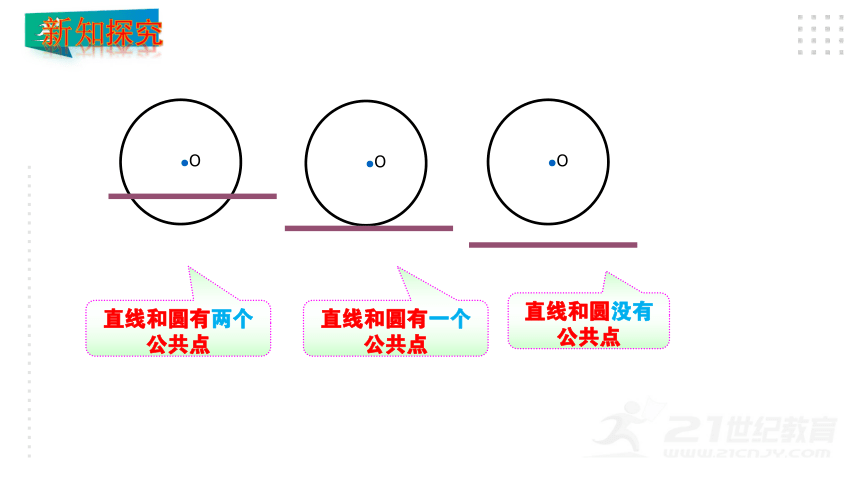
通过“旭日东升”这种自然现象大家说说,直线和圆的位置关系有哪几种
那直线与圆的公共点个数的有什么变化吗?公共点最少时有几个?最多时又有几个?
直线与圆有三种位置关系.
新知探究
●O
●O
●O
直线和圆有两个公共点
直线和圆有一个公共点
直线和圆没有公共点
新知探究
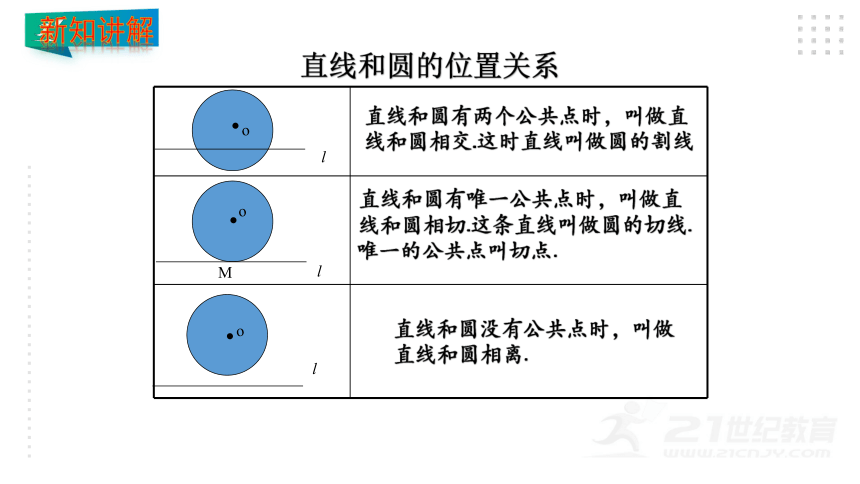
直线和圆的位置关系
l
l
l
直线和圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切.这条直线叫做圆的切线.唯一的公共点叫切点.
直线和圆没有公共点时,叫做直线和圆相离.
o
o
o
M
新知讲解
看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
相离
相切
相交
相交
l
l
l
l
·O
·O
·O
·O
新知探究
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
点和圆的三种位置关系
A
A
A
o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
d仿照这种方法怎样判断“直线和圆的位置关系”?
温故知新
O
l
┐
d
r
o
l
2.直线和圆相切
┐
d
r
d = r
O
l
3.直线和圆相交
d < r
d
┐
r
1.直线和圆相离
d > r
直线和圆的位置关系
令圆心O到直线l的距离为 d,圆的半径为 r
新知探究
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________ 的个数来判断;
(2)根据性质,由 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
归纳总结
1.下图中直线l是⊙O的切线的是( )
2.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为(C)
A.相离 B.相切
C.相交 D.无法确定
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是(D)
A.相离 B.相切
C.相交 D.相切或相交
2.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离 B.相切
C.相交 D.无法确定
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
C
C
D
跟踪练习
例1 已知 Rt△ABC的斜边AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与圆C相切
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB.分别有怎样的位置关系
典例精讲
解:过点C作CD⊥AB于点D,
∵Rt△ABC的斜边AB=8,AC=4,
∴CB2=AB2-AC2
CB=4√3,
∴CD=2√3,∴当半径R等于2√3时,AB与⊙O相切.
(2)由(1)可知,圆心C到 AB的距离d=2√3 cm,
所以
当r=2cm时,d<r, 圆C与AB相交;
当r=4cm时,d>r,圆C与AB相离.
1、在Rt△ABC中,∠C=90°,∠B=30°,O是AB上的一点,OA=m,圆O的半径为r.当r与m 满足怎样的关系时,
(1)AC与○0相交 (2)AC与○O相切
(3)AC与○0相离
解:作OH⊥AC于点H,∵∠C=90°,∠B=30° ∴∠A=60°
在Rt△OAH中,
合作共学
新知讲解
圆 的 切 线 性 质
圆的切线垂直于经过切点的半径
如图,直线L与圆O相切与点A,那么OA⊥L,为什么?
设直线L是圆O的切线,切点为A。
假设直线L不垂直于半径OA,那么我们通过圆心O作直线L的垂线,垂足为A/
在前面的点与直线的关系中我们知道:“点到直线上的任意点的距离,以垂线段最短”。
所以有OA'根据圆的定义,则A/一定在圆内。
由切线的定义:切线L与圆O只有一个公共点A,因此上述假设与本定义矛盾。
由此可证L必垂直于OA。
A/
新知讲解
反证法
1.(2020·重庆)如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=20°,则∠AOB的度数为( )
A.40° B.50° C.60° D.70°
2.(2019·郑州一中模拟)如图,P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=4,则线段BP的长为( )
A.6 B.4 C.4 D.8
合作共学
D
圆的切线垂直于经过切点的半径
C
特别注意:利用切线的性质解题时,常常借助口诀“见切点,连半径”解题.
1.(2020·哈尔滨)如图,AB为⊙O的切线,点A为切点,OB交⊙O于点C,点D在⊙O上,连接AD,CD,OA.若∠ADC=35°,则∠ABO的度数为(B)
A.25° B.20° C.30° D.35°
2.如图,两同心圆的大圆半径长为5 cm,小圆半径长为3 cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8_cm.
如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E. 求证:∠A=∠ADE.
典例精讲
证明:连接OD.
∵DE是切线,∴∠ODE=90°.
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO.
∴∠A=∠ADE.
见切点,连半径
2、如图,一枚直径为d的硬币沿着直线滚动一圈,圆心经过的距离是多少?
合作共学
解:如图,硬币经过的距离为硬币的周长减直径,根据圆形周长公式得:l=πd.所以经过的距离为πd-d
本题关键:理解直线与圆相切时,半径垂直于经过切点的切线.
3、为了测量一个光盘的直径,小明把直尺,光盘和三角尺按如图所示放置于桌面上,并量的AB=6厘米,这张光盘的直径是多少
合作共学
解析:设光盘的圆心为O,连接OC, OB, OA, 如图所示:
由切线的性质得到OB⊥AB,在Rt△AOB中,
由tan60°等于对边OB与邻边AB之比,
将AB及tan60°的值代入,求出OB的长,即为圆的半径,
进而确定出圆的直径.
∵AC,AB分别为圆O的切线,
∴AO为∠CAB的平分线,OC⊥AC,OB⊥AB,
又∠CAD=60°,
∴∠OAC=∠OAB=60°,
在Rt△AOB中,∠OAB=60°,AB=6cm,
∴OB=6√3cm
∴直径为12√3cm.
解:设光盘的圆心为O,连接OC, OB, OA, 如图所示:
合作共学
1.了解了直线与圆的三种位置关系;
2.学习了判断直线与圆的位置关系的两种方法
3.掌握“见切点,连半径”口诀解题.
从交点个数上;
从d与半径r的大小上;
北师版九年级下册 圆
§3.6.1 直线与圆的位置关系
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离d 与半径r 之间的关系来判定它们.
2.理解并掌握“切线的性质”,能灵活运用“见切点,连半径”口诀解题.
通过“旭日东升”这种自然现象大家说说,直线和圆的位置关系有哪几种
那直线与圆的公共点个数的有什么变化吗?公共点最少时有几个?最多时又有几个?
直线与圆有三种位置关系.
新知探究
●O
●O
●O
直线和圆有两个公共点
直线和圆有一个公共点
直线和圆没有公共点
新知探究
直线和圆的位置关系
l
l
l
直线和圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切.这条直线叫做圆的切线.唯一的公共点叫切点.
直线和圆没有公共点时,叫做直线和圆相离.
o
o
o
M
新知讲解
看图判断直线l与 ⊙O的位置关系
(1)
(2)
(3)
(4)
相离
相切
相交
相交
l
l
l
l
·O
·O
·O
·O
新知探究
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
点和圆的三种位置关系
A
A
A
o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
d
温故知新
O
l
┐
d
r
o
l
2.直线和圆相切
┐
d
r
d = r
O
l
3.直线和圆相交
d < r
d
┐
r
1.直线和圆相离
d > r
直线和圆的位置关系
令圆心O到直线l的距离为 d,圆的半径为 r
新知探究
判定直线 与圆的位置关系的方法有____种:
(1)根据定义,由________________ 的个数来判断;
(2)根据性质,由 的关系来判断。
在实际应用中,常采用第二种方法判定。
两
直线 与圆的公共点
圆心到直线的距离d与半径r
归纳总结
1.下图中直线l是⊙O的切线的是( )
2.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为(C)
A.相离 B.相切
C.相交 D.无法确定
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是(D)
A.相离 B.相切
C.相交 D.相切或相交
2.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离 B.相切
C.相交 D.无法确定
3.已知一条直线与圆有公共点,则这条直线与圆的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
C
C
D
跟踪练习
例1 已知 Rt△ABC的斜边AB=8 cm,AC=4 cm.
(1)以点C为圆心作圆,当半径为多长时,AB与圆C相切
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB.分别有怎样的位置关系
典例精讲
解:过点C作CD⊥AB于点D,
∵Rt△ABC的斜边AB=8,AC=4,
∴CB2=AB2-AC2
CB=4√3,
∴CD=2√3,∴当半径R等于2√3时,AB与⊙O相切.
(2)由(1)可知,圆心C到 AB的距离d=2√3 cm,
所以
当r=2cm时,d<r, 圆C与AB相交;
当r=4cm时,d>r,圆C与AB相离.
1、在Rt△ABC中,∠C=90°,∠B=30°,O是AB上的一点,OA=m,圆O的半径为r.当r与m 满足怎样的关系时,
(1)AC与○0相交 (2)AC与○O相切
(3)AC与○0相离
解:作OH⊥AC于点H,∵∠C=90°,∠B=30° ∴∠A=60°
在Rt△OAH中,
合作共学
新知讲解
圆 的 切 线 性 质
圆的切线垂直于经过切点的半径
如图,直线L与圆O相切与点A,那么OA⊥L,为什么?
设直线L是圆O的切线,切点为A。
假设直线L不垂直于半径OA,那么我们通过圆心O作直线L的垂线,垂足为A/
在前面的点与直线的关系中我们知道:“点到直线上的任意点的距离,以垂线段最短”。
所以有OA'
由切线的定义:切线L与圆O只有一个公共点A,因此上述假设与本定义矛盾。
由此可证L必垂直于OA。
A/
新知讲解
反证法
1.(2020·重庆)如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=20°,则∠AOB的度数为( )
A.40° B.50° C.60° D.70°
2.(2019·郑州一中模拟)如图,P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=4,则线段BP的长为( )
A.6 B.4 C.4 D.8
合作共学
D
圆的切线垂直于经过切点的半径
C
特别注意:利用切线的性质解题时,常常借助口诀“见切点,连半径”解题.
1.(2020·哈尔滨)如图,AB为⊙O的切线,点A为切点,OB交⊙O于点C,点D在⊙O上,连接AD,CD,OA.若∠ADC=35°,则∠ABO的度数为(B)
A.25° B.20° C.30° D.35°
2.如图,两同心圆的大圆半径长为5 cm,小圆半径长为3 cm,大圆的弦AB与小圆相切,切点为C,则弦AB的长是8_cm.
如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E. 求证:∠A=∠ADE.
典例精讲
证明:连接OD.
∵DE是切线,∴∠ODE=90°.
∴∠ADE+∠BDO=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO.
∴∠A=∠ADE.
见切点,连半径
2、如图,一枚直径为d的硬币沿着直线滚动一圈,圆心经过的距离是多少?
合作共学
解:如图,硬币经过的距离为硬币的周长减直径,根据圆形周长公式得:l=πd.所以经过的距离为πd-d
本题关键:理解直线与圆相切时,半径垂直于经过切点的切线.
3、为了测量一个光盘的直径,小明把直尺,光盘和三角尺按如图所示放置于桌面上,并量的AB=6厘米,这张光盘的直径是多少
合作共学
解析:设光盘的圆心为O,连接OC, OB, OA, 如图所示:
由切线的性质得到OB⊥AB,在Rt△AOB中,
由tan60°等于对边OB与邻边AB之比,
将AB及tan60°的值代入,求出OB的长,即为圆的半径,
进而确定出圆的直径.
∵AC,AB分别为圆O的切线,
∴AO为∠CAB的平分线,OC⊥AC,OB⊥AB,
又∠CAD=60°,
∴∠OAC=∠OAB=60°,
在Rt△AOB中,∠OAB=60°,AB=6cm,
∴OB=6√3cm
∴直径为12√3cm.
解:设光盘的圆心为O,连接OC, OB, OA, 如图所示:
合作共学
1.了解了直线与圆的三种位置关系;
2.学习了判断直线与圆的位置关系的两种方法
3.掌握“见切点,连半径”口诀解题.
从交点个数上;
从d与半径r的大小上;
