人教版七年级上册4.2 直线、射线、线段 同步练习(word解析版)
文档属性
| 名称 | 人教版七年级上册4.2 直线、射线、线段 同步练习(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 84.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 13:46:05 | ||
图片预览




文档简介
4.2 直线、射线、线段
一 、单选题(本大题共14小题,共42分)
1.如图所示,点,,,在同一条直线上,则图中线段的条数有
A. 条 B. 条 C. 条 D. 条
2.如图,点是线段的中点,,若,则
A. B. C. D.
3.如图,点在线段上,是线段的中点,下列关系式与图不相符的是
A. B.
C. D.
4.如图,已知线段厘米,为的中点,点在上,为的中点,且厘米.则的长为
A. 厘米 B. 厘米 C. 厘米 D. 厘米
5.下列说法中正确的语句共有
①直线与直线是同一条直线;
②线段与线段表示同一条线段;
③射线与射线表示同一条射线;
④延长射线至,使;
⑤延长线段至,使;
⑥直线总比线段长.
A. 个 B. 个 C. 个 D. 个
6.下列画图语句中,正确的是
A. 画射线 B. 画出、两点的距离
C. 延长射线 D. 连接、两点
7.如果,、三点在同一直线上,且线段,,若为的中点,那么,两点之间的距离为
A. B. C. 或 D. 无法确定
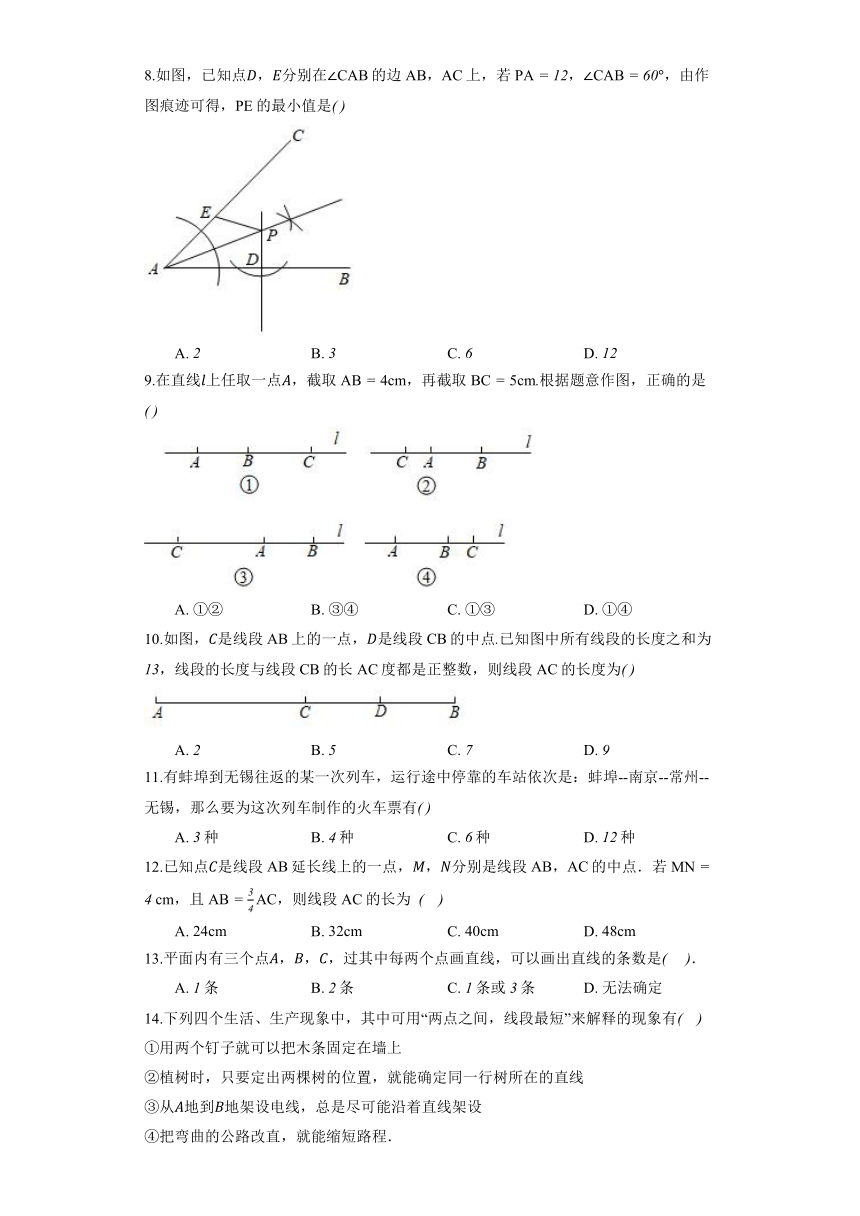
8.如图,已知点,分别在的边,上,若,,由作图痕迹可得,的最小值是
A. B. C. D.
9.在直线上任取一点,截取,再截取根据题意作图,正确的是
A. ①② B. ③④ C. ①③ D. ①④
10.如图,是线段上的一点,是线段的中点已知图中所有线段的长度之和为,线段的长度与线段的长度都是正整数,则线段的长度为
A. B. C. D.
11.有蚌埠到无锡往返的某一次列车,运行途中停靠的车站依次是:蚌埠--南京--常州--无锡,那么要为这次列车制作的火车票有
A. 种 B. 种 C. 种 D. 种
12.已知点是线段延长线上的一点,,分别是线段,的中点.若,且,则线段的长为
A. B. C. D.
13.平面内有三个点,,,过其中每两个点画直线,可以画出直线的条数是 .
A. 条 B. 条 C. 条或条 D. 无法确定
14.下列四个生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有
①用两个钉子就可以把木条固定在墙上
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
③从地到地架设电线,总是尽可能沿着直线架设
④把弯曲的公路改直,就能缩短路程.
A. ①② B. ①③ C. ②④ D. ③④
二 、填空题(本大题共6小题,共18分)
15.已知线段长为,点为射线上一点,若线段与其中一条线段是另外一条线段长的倍,则______.
16.已知点、、在同一条直线上,若,,点、分别是线段、的中点,则线段的长为 ______.
17.如图,已知点,,,在同一直线上,且线,那么图中所有线段的长度之和是______
18.如图,小颖用剪刀沿直线把一片平整的树叶剪掉一部分,发现剩下的树叶的周长比原来的树叶周长小,其数学原理是______.
19.如图,点为线段上一点,::,、两点分别、的中点,若线段,则______
20.已知,,三点在同一条直线上,,,则线段______.
三 、解答题(本大题共4小题,共32分)
21.(8分)尺规作图:如图,已知线段、、,用直尺和圆规作出一条线段,使它等于不要求写作法,但要保留作图痕迹
22.(8分)如图,已知线段,请用尺规作图法在线段的延长线上求作一点,使得保留作图痕迹,不写作法
23.(8分)如图,已知线段,延长至,使得,
求的长;
若是的中点,是的中点,求的长.
24.(8分)如图,点是线段的中点,点在上,且
若,求线段的长.
若,求线段的长.
答案和解析
1.【答案】D;
【解析】解:由图可得,线段有:线段、线段、线段、线段、线段、线段,共条.
故选:
根据线段的定义,写出所有线段后再计算条数.
此题主要考查线段的定义,注意解决计数问题时要做到不重不漏.
2.【答案】A;
【解析】解:点是线段的中点,
,
,,
,
,
,
,
故选:
根据线段中点的性质,可得的长,可得的长.
此题主要考查了两点间的距离,利用了线段中点的性质.
3.【答案】C;
【解析】解:是线段的中点,
A.由,得,故,那么中关系式正确,即不符合题意.
B.由,故,那么中关系式正确,即不符合题意.
C.由,故,无法推断出,那么中关系式不正确,即符合题意.
D.由,故,,得,那么中关系式正确,即不符合题意.
故选:
由是线段的中点,得,再根据线段的和差关系解决此题.
此题主要考查线段中点以及线段的和差关系,熟练掌握线段中点以及线段的和差关系是解决本题的关键.
4.【答案】C;
【解析】解:厘米,为的中点,
厘米,
为的中点,且厘米,
厘米,
厘米.
故选:
先求出的长,再根据为的中点,且厘米,求出的长,利用即可求出的长.
利用中点性质转化线段之间的倍分关系是解答该题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
5.【答案】B;
【解析】解:①直线与直线是同一条直线,原说法正确;
②线段与线段表示同一条线段,原说法正确;
③射线与射线表示的不是同一条射线,因为端点不同,所以原说法错误;
④不能说延长射线至,因为射线能向一方无限延长,所以原说法错误;
⑤延长线段至,使,原说法正确;
⑥直线与线段不能比较长短,因为直线能向两方无限延长,所以原说法错误.
正确的说法有个.
故选:
根据直线、射线、线段的定义和性质解答即可.
此题主要考查了直线、射线、线段.熟练掌握直线、射线、线段的定义和特性是解答该题的关键.
6.【答案】D;
【解析】解:、射线无限长,所以选项不符合题意;
、量出、点的距离,所以选项不符合题意;
、射线不需要延长,只能反向延长射线,所以选项不符合题意;
、用直尺可以连接、两点,所以选项符合题意.
故选:
利用射线的定义对、进行判断;根据两点间的距离的定义和线段的定义对、进行判断.
此题主要考查了作图尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
7.【答案】C;
【解析】解:如图,当点在线段的延长线上时,
,
为的中点,
;
如图,当点在线段上时,
,
为的中点,
;
综上所述,,两点之间的距离为或,
故选:
因为不清楚,,三点的位置,所以需要分点在线段的延长线上和点在线段上两种情况分别进行计算.
此题主要考查了两点间的距离,体现了分类讨论的数学思想,题目中没有图形,不清楚,,三点的位置,分类讨论是解答该题的关键,不要漏解.
8.【答案】C;
【解析】解:根据作图痕迹可知:是的平分线,
,
,
当时,最小,
,,
到的最小值是:
故选:
根据作图痕迹可得,是的平分线,根据角平分线上的点到角的两边距离相等即可得的最小值.
此题主要考查了作图基本作图,解决本题的关键是掌握角平分线的性质.
9.【答案】A;
【解析】解:当点在的延长线上时,如图①;
当点在的延长线上时,如图②.
故选:
利用基本作图和分类讨论的思想对各选项进行判断.
此题主要考查了作图复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
10.【答案】A;
【解析】解:设,,则,
即:,
得:,
因为线段的长度与线段的长度都是正整数,
所以最大为,
可知:,,符合题意;
所以
故选:
可以设出和的长,再根据图中所有线段的长度之和为,即可列出等式,再根据线段的长度与线段的长度都是正整数,即可求出答案.
此题主要考查了比较线段长短的知识,有一定难度,根据题意列出方程式,并探讨解的合理性是关键.
11.【答案】C;
【解析】解:根据分析可知,这次列车制作的火车票的总数种
故选:
由题意可知:由蚌埠要经过个地方,所以要制作种车票;由南京北要经过个地方,所以要制作种车票;由常州城要经过个地方,所要制作种车票;结合上述结论,通过往返计算出答案.
此题主要考查了直线、射线、线段,解题时要注意同两个站之间的车票是否有起点站和终点站的区分.
12.【答案】B;
【解析】
这道题主要考查两点之间的距离,线段中点的性质,线段的和差,关键在于运用数形结合的思想和熟练掌握相关的知识.
根据题意画出图形,由,设,则,再根据、分别是线段、的中点得出和,再根据列出方程,求出的值,从而确定的长.
解:如图,
,设,则,
、分别是线段、的中点,
,,
,,
,
,
.
故选:.
13.【答案】C;
【解析】
该题考查了直线、射线、线段,本题的关键是进行分类讨论,将三个点进行不同的排列,可得两个结果.
解:如图可以画条直线或条直线,
故选C.
14.【答案】D;
【解析】
分别利用直线的性质以及线段的性质分析得出答案.
此题主要考查了直线的性质以及线段的性质,正确把握直线与线段的性质是解题关键.
解:①用两个钉子就可以把木条固定在墙上,是两点确定一条之间,故此选项错误;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条之间,故此选项错误;
③从地到地架设电线,总是尽可能沿着直线架设,是两点之间,线段最短,故此选项正确;
④把弯曲的公路改直,就能缩短路程,是两点之间,线段最短,故此选项正确;
故选:.
15.【答案】18或3或9;
【解析】解:分两种情况:
①如图,当时,;
②如图,当时,
,
或;
综上,或或
故答案为:或或
分两种情况:或,画图根据线段的和差关系可得结论.
此题主要考查了线段的和差关系,抓住题目中“线段与其中一条线段是另外一条线段长的倍”分类讨论各种可能出现的情况是解答该题的关键.
16.【答案】7或1;
【解析】解:当点在线段上时,
、分别为线段、的中点,
,,
;
当点在线段的反向延长线上时,
、分别为线段、的中点,
,,
,
故答案为:或
分类讨论:点在线段上或点在线段的反向延长线上,根据中点定义,可得与的关系,与的关系,可根据线段的和差,可得答案.
此题主要考查了两点间的距离,利用线段的和差并分类讨论是解题关键.
17.【答案】;
【解析】
此题主要考查了求两点之间的距离,能找出所有线段是解此题的关键.
先找出所有线段,再代入求出即可.
解:线段,
,
故答案为:
18.【答案】两点之间,线段最短;
【解析】解:用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是两点之间,线段最短.
故答案为:两点之间,线段最短.
两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短,根据线段的性质解答即可.
此题主要考查了线段的性质,正确联系实际生活是解题关键.
19.【答案】10;
【解析】解:设,由已知得:
,,
、两点分别为、的中点,
,,
,
,
解得:,
则的长为,
故答案为:
在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,根据题目中几何图形,再根据题意进行计算.
此题主要考查了两点间的距离.利用中点性质转化线段之间的倍分关系是解答该题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
20.【答案】9cm或15cm;
【解析】解:当点在的延长线上时,如图,
当点在的延长线上时,如图,
,
综上所述,线段的长为或
故答案为或
讨论:当点在的延长线上时,如图,则;当点在的延长线上时,如图,则
此题主要考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.注意分类讨论思想的运用.
21.【答案】解:如图,线段AD即为所求.
;
【解析】
作射线,在射线上顺次截取,,在线段上截取,则线段即为所求.
此题主要考查作图复杂作图,解答该题的关键是掌握线段的和差定义,灵活运用所学知识解决问题.
22.【答案】解:如图,点C即为所求.
;
【解析】
延长,在的延长线上截取即可.
此题主要考查了尺规作图基本作图,解决此题的关键是清楚作等长线段的尺规作图的步骤与原来.
23.【答案】解:(1)∵BC=AB,AB=24cm,
∴BC=×24cm=12cm,
∴AC=AB+BC=36cm;
(2)∵D是AB的中点,E是AC的中点,
∴AD=AB=12cm,AE=AC=18cm,
∴DE=18cm-12cm=6cm.;
【解析】
根据与的关系可得,由可得答案;
根据线段中点的定义分别求出和的长度,再利用线段的和差得出答案.
此题主要考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答该题的关键.
24.【答案】解:(1)∵AD=4cm,且AD=AB,
∴AB=12cm,
∵点C是线段AB的中点,
∴AC=×12=6cm,
∴CD=AC-AD=2cm;
(2)∵AD=AB,
∴设AD=x,则AB=3x,
∵点C是线段AB的中点,
∴AC=xcm,
∴CD=x-x=3,解得x=6,
∴AB=3x=18cm.;
【解析】
根据与的关系可得,再利用线段中点的定义和线段的和差可得答案;
利用线段的和差列方程可得答案.
此题主要考查的是两点间的距离的计算,利用线段的和差找到各线段之间的关系是解答该题的关键.
一 、单选题(本大题共14小题,共42分)
1.如图所示,点,,,在同一条直线上,则图中线段的条数有
A. 条 B. 条 C. 条 D. 条
2.如图,点是线段的中点,,若,则
A. B. C. D.
3.如图,点在线段上,是线段的中点,下列关系式与图不相符的是
A. B.
C. D.
4.如图,已知线段厘米,为的中点,点在上,为的中点,且厘米.则的长为
A. 厘米 B. 厘米 C. 厘米 D. 厘米
5.下列说法中正确的语句共有
①直线与直线是同一条直线;
②线段与线段表示同一条线段;
③射线与射线表示同一条射线;
④延长射线至,使;
⑤延长线段至,使;
⑥直线总比线段长.
A. 个 B. 个 C. 个 D. 个
6.下列画图语句中,正确的是
A. 画射线 B. 画出、两点的距离
C. 延长射线 D. 连接、两点
7.如果,、三点在同一直线上,且线段,,若为的中点,那么,两点之间的距离为
A. B. C. 或 D. 无法确定
8.如图,已知点,分别在的边,上,若,,由作图痕迹可得,的最小值是
A. B. C. D.
9.在直线上任取一点,截取,再截取根据题意作图,正确的是
A. ①② B. ③④ C. ①③ D. ①④
10.如图,是线段上的一点,是线段的中点已知图中所有线段的长度之和为,线段的长度与线段的长度都是正整数,则线段的长度为
A. B. C. D.
11.有蚌埠到无锡往返的某一次列车,运行途中停靠的车站依次是:蚌埠--南京--常州--无锡,那么要为这次列车制作的火车票有
A. 种 B. 种 C. 种 D. 种
12.已知点是线段延长线上的一点,,分别是线段,的中点.若,且,则线段的长为
A. B. C. D.
13.平面内有三个点,,,过其中每两个点画直线,可以画出直线的条数是 .
A. 条 B. 条 C. 条或条 D. 无法确定
14.下列四个生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有
①用两个钉子就可以把木条固定在墙上
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线
③从地到地架设电线,总是尽可能沿着直线架设
④把弯曲的公路改直,就能缩短路程.
A. ①② B. ①③ C. ②④ D. ③④
二 、填空题(本大题共6小题,共18分)
15.已知线段长为,点为射线上一点,若线段与其中一条线段是另外一条线段长的倍,则______.
16.已知点、、在同一条直线上,若,,点、分别是线段、的中点,则线段的长为 ______.
17.如图,已知点,,,在同一直线上,且线,那么图中所有线段的长度之和是______
18.如图,小颖用剪刀沿直线把一片平整的树叶剪掉一部分,发现剩下的树叶的周长比原来的树叶周长小,其数学原理是______.
19.如图,点为线段上一点,::,、两点分别、的中点,若线段,则______
20.已知,,三点在同一条直线上,,,则线段______.
三 、解答题(本大题共4小题,共32分)
21.(8分)尺规作图:如图,已知线段、、,用直尺和圆规作出一条线段,使它等于不要求写作法,但要保留作图痕迹
22.(8分)如图,已知线段,请用尺规作图法在线段的延长线上求作一点,使得保留作图痕迹,不写作法
23.(8分)如图,已知线段,延长至,使得,
求的长;
若是的中点,是的中点,求的长.
24.(8分)如图,点是线段的中点,点在上,且
若,求线段的长.
若,求线段的长.
答案和解析
1.【答案】D;
【解析】解:由图可得,线段有:线段、线段、线段、线段、线段、线段,共条.
故选:
根据线段的定义,写出所有线段后再计算条数.
此题主要考查线段的定义,注意解决计数问题时要做到不重不漏.
2.【答案】A;
【解析】解:点是线段的中点,
,
,,
,
,
,
,
故选:
根据线段中点的性质,可得的长,可得的长.
此题主要考查了两点间的距离,利用了线段中点的性质.
3.【答案】C;
【解析】解:是线段的中点,
A.由,得,故,那么中关系式正确,即不符合题意.
B.由,故,那么中关系式正确,即不符合题意.
C.由,故,无法推断出,那么中关系式不正确,即符合题意.
D.由,故,,得,那么中关系式正确,即不符合题意.
故选:
由是线段的中点,得,再根据线段的和差关系解决此题.
此题主要考查线段中点以及线段的和差关系,熟练掌握线段中点以及线段的和差关系是解决本题的关键.
4.【答案】C;
【解析】解:厘米,为的中点,
厘米,
为的中点,且厘米,
厘米,
厘米.
故选:
先求出的长,再根据为的中点,且厘米,求出的长,利用即可求出的长.
利用中点性质转化线段之间的倍分关系是解答该题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
5.【答案】B;
【解析】解:①直线与直线是同一条直线,原说法正确;
②线段与线段表示同一条线段,原说法正确;
③射线与射线表示的不是同一条射线,因为端点不同,所以原说法错误;
④不能说延长射线至,因为射线能向一方无限延长,所以原说法错误;
⑤延长线段至,使,原说法正确;
⑥直线与线段不能比较长短,因为直线能向两方无限延长,所以原说法错误.
正确的说法有个.
故选:
根据直线、射线、线段的定义和性质解答即可.
此题主要考查了直线、射线、线段.熟练掌握直线、射线、线段的定义和特性是解答该题的关键.
6.【答案】D;
【解析】解:、射线无限长,所以选项不符合题意;
、量出、点的距离,所以选项不符合题意;
、射线不需要延长,只能反向延长射线,所以选项不符合题意;
、用直尺可以连接、两点,所以选项符合题意.
故选:
利用射线的定义对、进行判断;根据两点间的距离的定义和线段的定义对、进行判断.
此题主要考查了作图尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.
7.【答案】C;
【解析】解:如图,当点在线段的延长线上时,
,
为的中点,
;
如图,当点在线段上时,
,
为的中点,
;
综上所述,,两点之间的距离为或,
故选:
因为不清楚,,三点的位置,所以需要分点在线段的延长线上和点在线段上两种情况分别进行计算.
此题主要考查了两点间的距离,体现了分类讨论的数学思想,题目中没有图形,不清楚,,三点的位置,分类讨论是解答该题的关键,不要漏解.
8.【答案】C;
【解析】解:根据作图痕迹可知:是的平分线,
,
,
当时,最小,
,,
到的最小值是:
故选:
根据作图痕迹可得,是的平分线,根据角平分线上的点到角的两边距离相等即可得的最小值.
此题主要考查了作图基本作图,解决本题的关键是掌握角平分线的性质.
9.【答案】A;
【解析】解:当点在的延长线上时,如图①;
当点在的延长线上时,如图②.
故选:
利用基本作图和分类讨论的思想对各选项进行判断.
此题主要考查了作图复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.
10.【答案】A;
【解析】解:设,,则,
即:,
得:,
因为线段的长度与线段的长度都是正整数,
所以最大为,
可知:,,符合题意;
所以
故选:
可以设出和的长,再根据图中所有线段的长度之和为,即可列出等式,再根据线段的长度与线段的长度都是正整数,即可求出答案.
此题主要考查了比较线段长短的知识,有一定难度,根据题意列出方程式,并探讨解的合理性是关键.
11.【答案】C;
【解析】解:根据分析可知,这次列车制作的火车票的总数种
故选:
由题意可知:由蚌埠要经过个地方,所以要制作种车票;由南京北要经过个地方,所以要制作种车票;由常州城要经过个地方,所要制作种车票;结合上述结论,通过往返计算出答案.
此题主要考查了直线、射线、线段,解题时要注意同两个站之间的车票是否有起点站和终点站的区分.
12.【答案】B;
【解析】
这道题主要考查两点之间的距离,线段中点的性质,线段的和差,关键在于运用数形结合的思想和熟练掌握相关的知识.
根据题意画出图形,由,设,则,再根据、分别是线段、的中点得出和,再根据列出方程,求出的值,从而确定的长.
解:如图,
,设,则,
、分别是线段、的中点,
,,
,,
,
,
.
故选:.
13.【答案】C;
【解析】
该题考查了直线、射线、线段,本题的关键是进行分类讨论,将三个点进行不同的排列,可得两个结果.
解:如图可以画条直线或条直线,
故选C.
14.【答案】D;
【解析】
分别利用直线的性质以及线段的性质分析得出答案.
此题主要考查了直线的性质以及线段的性质,正确把握直线与线段的性质是解题关键.
解:①用两个钉子就可以把木条固定在墙上,是两点确定一条之间,故此选项错误;
②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线,是两点确定一条之间,故此选项错误;
③从地到地架设电线,总是尽可能沿着直线架设,是两点之间,线段最短,故此选项正确;
④把弯曲的公路改直,就能缩短路程,是两点之间,线段最短,故此选项正确;
故选:.
15.【答案】18或3或9;
【解析】解:分两种情况:
①如图,当时,;
②如图,当时,
,
或;
综上,或或
故答案为:或或
分两种情况:或,画图根据线段的和差关系可得结论.
此题主要考查了线段的和差关系,抓住题目中“线段与其中一条线段是另外一条线段长的倍”分类讨论各种可能出现的情况是解答该题的关键.
16.【答案】7或1;
【解析】解:当点在线段上时,
、分别为线段、的中点,
,,
;
当点在线段的反向延长线上时,
、分别为线段、的中点,
,,
,
故答案为:或
分类讨论:点在线段上或点在线段的反向延长线上,根据中点定义,可得与的关系,与的关系,可根据线段的和差,可得答案.
此题主要考查了两点间的距离,利用线段的和差并分类讨论是解题关键.
17.【答案】;
【解析】
此题主要考查了求两点之间的距离,能找出所有线段是解此题的关键.
先找出所有线段,再代入求出即可.
解:线段,
,
故答案为:
18.【答案】两点之间,线段最短;
【解析】解:用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是两点之间,线段最短.
故答案为:两点之间,线段最短.
两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短,根据线段的性质解答即可.
此题主要考查了线段的性质,正确联系实际生活是解题关键.
19.【答案】10;
【解析】解:设,由已知得:
,,
、两点分别为、的中点,
,,
,
,
解得:,
则的长为,
故答案为:
在一条直线或线段上的线段的加减运算和倍数运算,首先明确线段间的相互关系,根据题目中几何图形,再根据题意进行计算.
此题主要考查了两点间的距离.利用中点性质转化线段之间的倍分关系是解答该题的关键,在不同的情况下灵活选用它的不同表示方法,有利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
20.【答案】9cm或15cm;
【解析】解:当点在的延长线上时,如图,
当点在的延长线上时,如图,
,
综上所述,线段的长为或
故答案为或
讨论:当点在的延长线上时,如图,则;当点在的延长线上时,如图,则
此题主要考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.注意分类讨论思想的运用.
21.【答案】解:如图,线段AD即为所求.
;
【解析】
作射线,在射线上顺次截取,,在线段上截取,则线段即为所求.
此题主要考查作图复杂作图,解答该题的关键是掌握线段的和差定义,灵活运用所学知识解决问题.
22.【答案】解:如图,点C即为所求.
;
【解析】
延长,在的延长线上截取即可.
此题主要考查了尺规作图基本作图,解决此题的关键是清楚作等长线段的尺规作图的步骤与原来.
23.【答案】解:(1)∵BC=AB,AB=24cm,
∴BC=×24cm=12cm,
∴AC=AB+BC=36cm;
(2)∵D是AB的中点,E是AC的中点,
∴AD=AB=12cm,AE=AC=18cm,
∴DE=18cm-12cm=6cm.;
【解析】
根据与的关系可得,由可得答案;
根据线段中点的定义分别求出和的长度,再利用线段的和差得出答案.
此题主要考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答该题的关键.
24.【答案】解:(1)∵AD=4cm,且AD=AB,
∴AB=12cm,
∵点C是线段AB的中点,
∴AC=×12=6cm,
∴CD=AC-AD=2cm;
(2)∵AD=AB,
∴设AD=x,则AB=3x,
∵点C是线段AB的中点,
∴AC=xcm,
∴CD=x-x=3,解得x=6,
∴AB=3x=18cm.;
【解析】
根据与的关系可得,再利用线段中点的定义和线段的和差可得答案;
利用线段的和差列方程可得答案.
此题主要考查的是两点间的距离的计算,利用线段的和差找到各线段之间的关系是解答该题的关键.
