2021-2022学年人教版数学九年级上册24.1.4圆周角 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.1.4圆周角 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 902.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-01 15:57:29 | ||
图片预览





文档简介
(共24张PPT)
24.1.4圆周角 课件
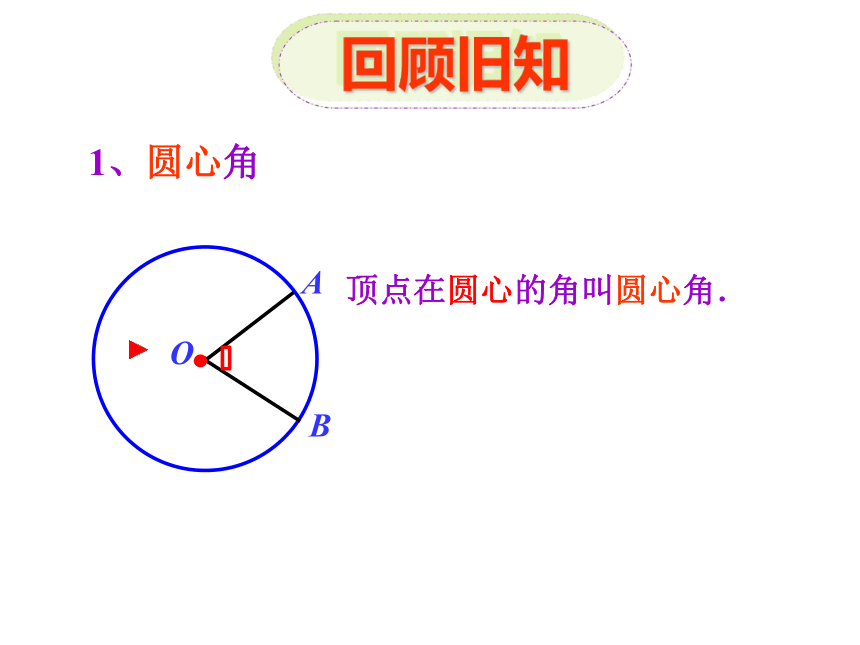
顶点在圆心的角叫圆心角.
·
O
B
A
回顾旧知
1、圆心角
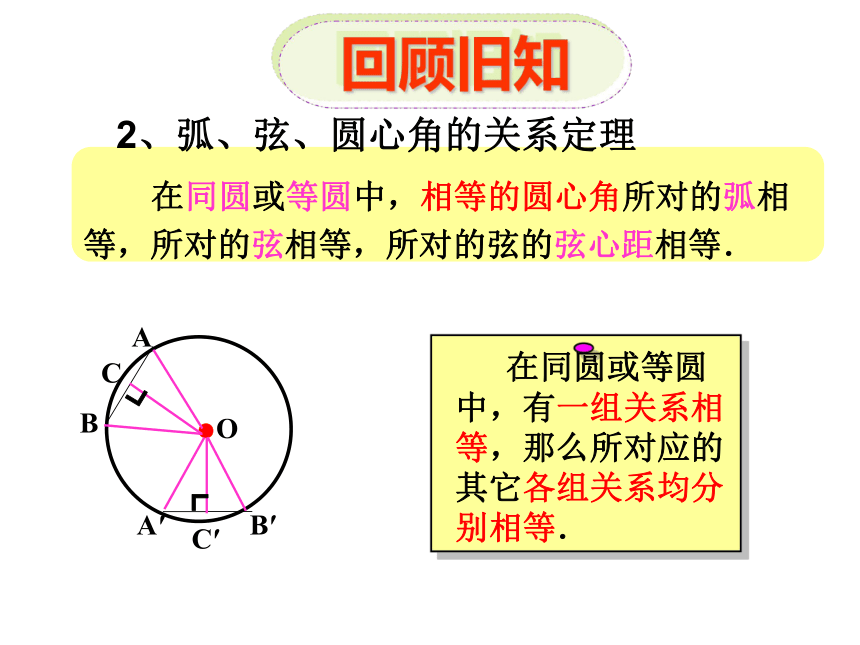
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
C
A′
B′
C′
┏
2、弧、弦、圆心角的关系定理
在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.
回顾旧知
某足球教练在考查学员定点射门的能力。足球教练在场地上画了一个圆,使得这个圆经过球门的两个门柱A、C。学员可在弧上B、D、E任意一点射门,如果你是学员,从射门角度大小考虑,你会选择在哪个点射门?为什么?
B
D
E
A
C
射门角度指射球点与两门柱的夹角
●O
B
A
C
D
E
射门角度指射球点与两门柱的夹角
在B、D、E处射门时,射门角度分别为
.
∠ABC、
∠ADC、
∠AEC
问题1: 这几个角是圆心角吗?
顶点在圆上,并且两边都和圆相交的角.
圆周角:
圆周角的两个特征
1、顶点在圆上
2、两边与圆相交
这三个角有何共同特点
这三个角叫什么角呢
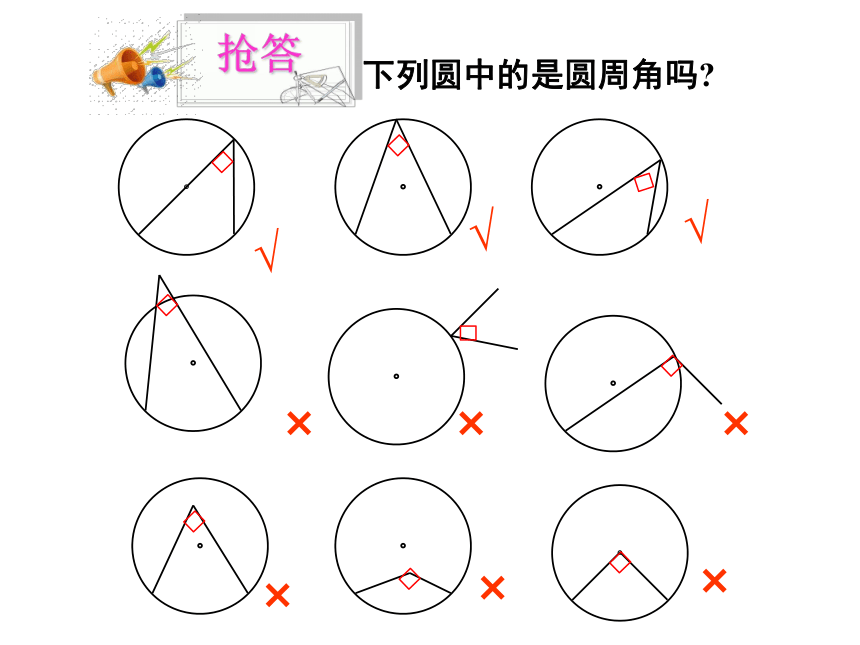
下列圆中的是圆周角吗
抢答
√
×
√
×
√
×
×
×
×
顶点在圆上,并且两边都和圆相交的角.
圆周角
·
E
D
B
A
C
O
抢答
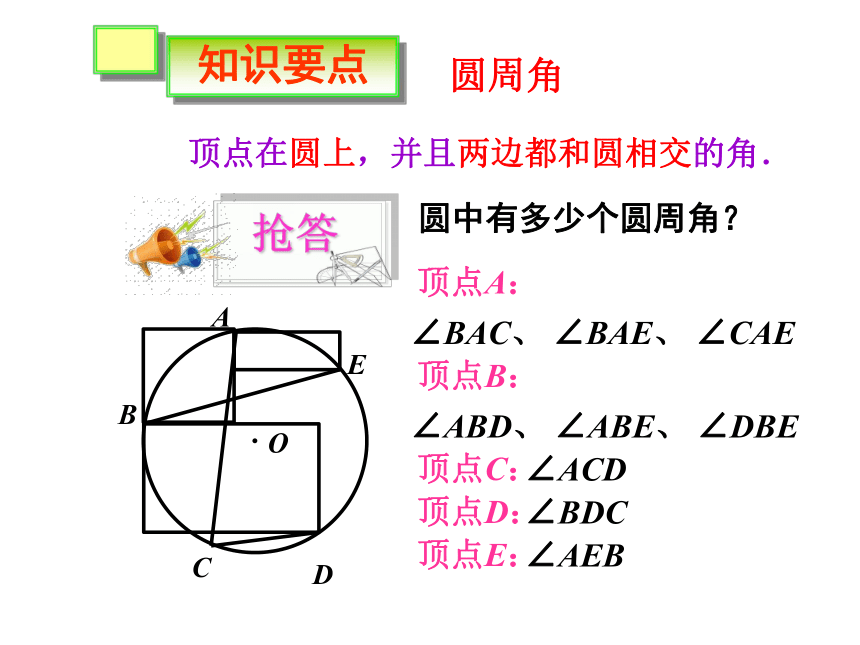
圆中有多少个圆周角?
顶点A:
∠BAC、 ∠BAE、 ∠CAE
顶点B:
∠ABD、 ∠ABE、 ∠DBE
顶点C:
∠ACD
顶点D:
顶点E:
∠BDC
∠AEB
知识要点
圆周角
●O
B
A
C
D
E
探 究
在圆2中画出弧AB所对的圆心角和三个不同的圆周角,并测量它们的度数,你能发现什么规律?
射门角度指射球点与两门柱的夹角
在B、D、E处射门时,射门角度分别为
.
∠ABC、
∠ADC、
∠AEC
问题2:弧AC所对的三个圆周角的
大小有什么关系
·
C
E
B
A
D
大胆猜测
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于圆心角的一半.
·
O
利用几何画板演示,让学生观察:同弧所对的圆周角与圆心有哪些不同的位置关系
●O
A
B
C
●O
A
B
C
●O
A
B
C
把这三种情况分别画在圆1圆3圆5中。
若要选一个图形来证明刚才的猜测,你认为哪一个最易证明,试证之
猜测:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于圆心角的一半.
友情提示:证文字题,要先写出已知,求证
证明
·
C
O
A
B
即
∵OA=OC,
∴∠A=∠C.
又∠BOC=∠A+∠C
∴∠BOC=2∠A
(1)圆心在圆周角的一条边上.
已知∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角
求证:
其它两种情况还要证明
●O
A
B
C
●O
A
B
C
●O
A
B
C
(2)圆心在圆周角的内部.
作直径AD,
利用(1)的结果,有
·
C
O
A
B
D
已知∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角
求证:
(3)圆心在圆周角的外部.
·
C
O
A
B
D
作直径AD,
利用(1)的结果,有
已知∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角
求证:
知识要点
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于圆心角的一半.
圆周角定理推论: (P85页方框)
在同圆或等圆中,如果两个圆周角相等它们所对的弧一定相等.
如何证明?
反过来: 在同圆或等圆中,如果两个圆周角相等,它们所对的弧相等吗?
2. 在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_______.
1. 在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=50°,则∠CAD=______.
20°
25°
随堂练习
3.P86 点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
由同弧来找相等的圆周角.
4.如图,AB是直径,则∠ACB=---- .
C
O
·
A
B
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
圆周角定理的推论
·
B
C1
O
C2
C3
┓
┓
┓
A
5、如图是中国共产主义青年团团旗上的图案,5个角的顶点A,B,C,D,E把外面的圆5等分,则∠A+∠B+∠C+∠D+∠E的度数是( ) A.180° B.150° C.135° D.120°
6、已知AB是⊙O的直径,AC,AD是弦,且AB=2,AC= ,AD=1,求圆周角∠CAD的度数。
6、已知AB是⊙O的直径,AC,AD是弦,且AB=2,AC= ,AD=1,求圆周角∠CAD的度数。
分类讨论 15°或105°
思考题:如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
课堂小结
顶点在圆上,并且两边都和圆相交的角.
1. 圆周角
2. 圆周角定理
A
B
C
课堂小结
4. 三种思想
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
3、圆周角定理的推论
从特殊到一般的思想.
分类讨论的思想
化归思想
作业:
P87习题24.1 4
思考题:如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
24.1.4圆周角 课件
顶点在圆心的角叫圆心角.
·
O
B
A
回顾旧知
1、圆心角
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.
●O
A
B
┓
C
A′
B′
C′
┏
2、弧、弦、圆心角的关系定理
在同圆或等圆中,有一组关系相等,那么所对应的其它各组关系均分别相等.
回顾旧知
某足球教练在考查学员定点射门的能力。足球教练在场地上画了一个圆,使得这个圆经过球门的两个门柱A、C。学员可在弧上B、D、E任意一点射门,如果你是学员,从射门角度大小考虑,你会选择在哪个点射门?为什么?
B
D
E
A
C
射门角度指射球点与两门柱的夹角
●O
B
A
C
D
E
射门角度指射球点与两门柱的夹角
在B、D、E处射门时,射门角度分别为
.
∠ABC、
∠ADC、
∠AEC
问题1: 这几个角是圆心角吗?
顶点在圆上,并且两边都和圆相交的角.
圆周角:
圆周角的两个特征
1、顶点在圆上
2、两边与圆相交
这三个角有何共同特点
这三个角叫什么角呢
下列圆中的是圆周角吗
抢答
√
×
√
×
√
×
×
×
×
顶点在圆上,并且两边都和圆相交的角.
圆周角
·
E
D
B
A
C
O
抢答
圆中有多少个圆周角?
顶点A:
∠BAC、 ∠BAE、 ∠CAE
顶点B:
∠ABD、 ∠ABE、 ∠DBE
顶点C:
∠ACD
顶点D:
顶点E:
∠BDC
∠AEB
知识要点
圆周角
●O
B
A
C
D
E
探 究
在圆2中画出弧AB所对的圆心角和三个不同的圆周角,并测量它们的度数,你能发现什么规律?
射门角度指射球点与两门柱的夹角
在B、D、E处射门时,射门角度分别为
.
∠ABC、
∠ADC、
∠AEC
问题2:弧AC所对的三个圆周角的
大小有什么关系
·
C
E
B
A
D
大胆猜测
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于圆心角的一半.
·
O
利用几何画板演示,让学生观察:同弧所对的圆周角与圆心有哪些不同的位置关系
●O
A
B
C
●O
A
B
C
●O
A
B
C
把这三种情况分别画在圆1圆3圆5中。
若要选一个图形来证明刚才的猜测,你认为哪一个最易证明,试证之
猜测:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于圆心角的一半.
友情提示:证文字题,要先写出已知,求证
证明
·
C
O
A
B
即
∵OA=OC,
∴∠A=∠C.
又∠BOC=∠A+∠C
∴∠BOC=2∠A
(1)圆心在圆周角的一条边上.
已知∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角
求证:
其它两种情况还要证明
●O
A
B
C
●O
A
B
C
●O
A
B
C
(2)圆心在圆周角的内部.
作直径AD,
利用(1)的结果,有
·
C
O
A
B
D
已知∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角
求证:
(3)圆心在圆周角的外部.
·
C
O
A
B
D
作直径AD,
利用(1)的结果,有
已知∠A是弧BC所对的圆周角,∠BOC是弧BC所对的圆心角
求证:
知识要点
圆周角定理
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于圆心角的一半.
圆周角定理推论: (P85页方框)
在同圆或等圆中,如果两个圆周角相等它们所对的弧一定相等.
如何证明?
反过来: 在同圆或等圆中,如果两个圆周角相等,它们所对的弧相等吗?
2. 在⊙O中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,则x=_______.
1. 在直径为AB的半圆中,O为圆心,C、D为半圆上的两点,∠COD=50°,则∠CAD=______.
20°
25°
随堂练习
3.P86 点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
由同弧来找相等的圆周角.
4.如图,AB是直径,则∠ACB=---- .
C
O
·
A
B
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
圆周角定理的推论
·
B
C1
O
C2
C3
┓
┓
┓
A
5、如图是中国共产主义青年团团旗上的图案,5个角的顶点A,B,C,D,E把外面的圆5等分,则∠A+∠B+∠C+∠D+∠E的度数是( ) A.180° B.150° C.135° D.120°
6、已知AB是⊙O的直径,AC,AD是弦,且AB=2,AC= ,AD=1,求圆周角∠CAD的度数。
6、已知AB是⊙O的直径,AC,AD是弦,且AB=2,AC= ,AD=1,求圆周角∠CAD的度数。
分类讨论 15°或105°
思考题:如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
在同圆(或等圆)中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
课堂小结
顶点在圆上,并且两边都和圆相交的角.
1. 圆周角
2. 圆周角定理
A
B
C
课堂小结
4. 三种思想
半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.
3、圆周角定理的推论
从特殊到一般的思想.
分类讨论的思想
化归思想
作业:
P87习题24.1 4
思考题:如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
同课章节目录
